圆锥曲线上一类定值问题的再推广
2022-03-05 09:19重庆市铜梁二中402560
中学数学研究(江西) 2022年3期
重庆市铜梁二中 (402560) 李 波
1 问题提出
文[1]中给出了圆锥曲线焦点弦引起的所分线段比值之和为定值的若干结论.比如以下两个结论:
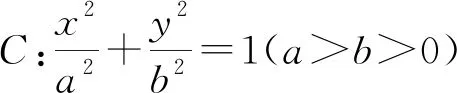
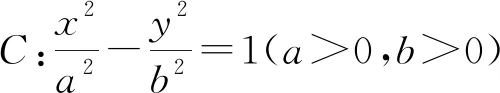
事实上,文[2]也给出了上面的两个命题,并提供了四种证明思路.在以上两个结论中,焦点F1,F2其实是x轴上一对关于原点对称的点.那么,对于x轴上其他的关于原点对称的点P1,P2,是否有类似的结论?进一步,P1,P2是y轴上的一对关于原点对称的,甚至是坐标轴之外的一对关于原点对称的点,λ1+λ2还会是定值吗?本文对这几个问题展开讨论,并对双曲线和椭圆上的类似问题给出解答.
2 问题解决
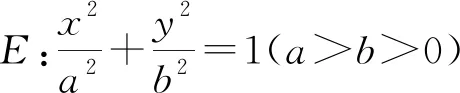

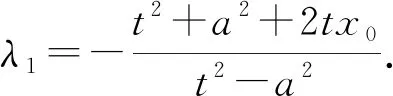
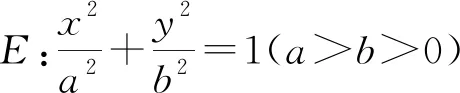
证法同性质1,此略.
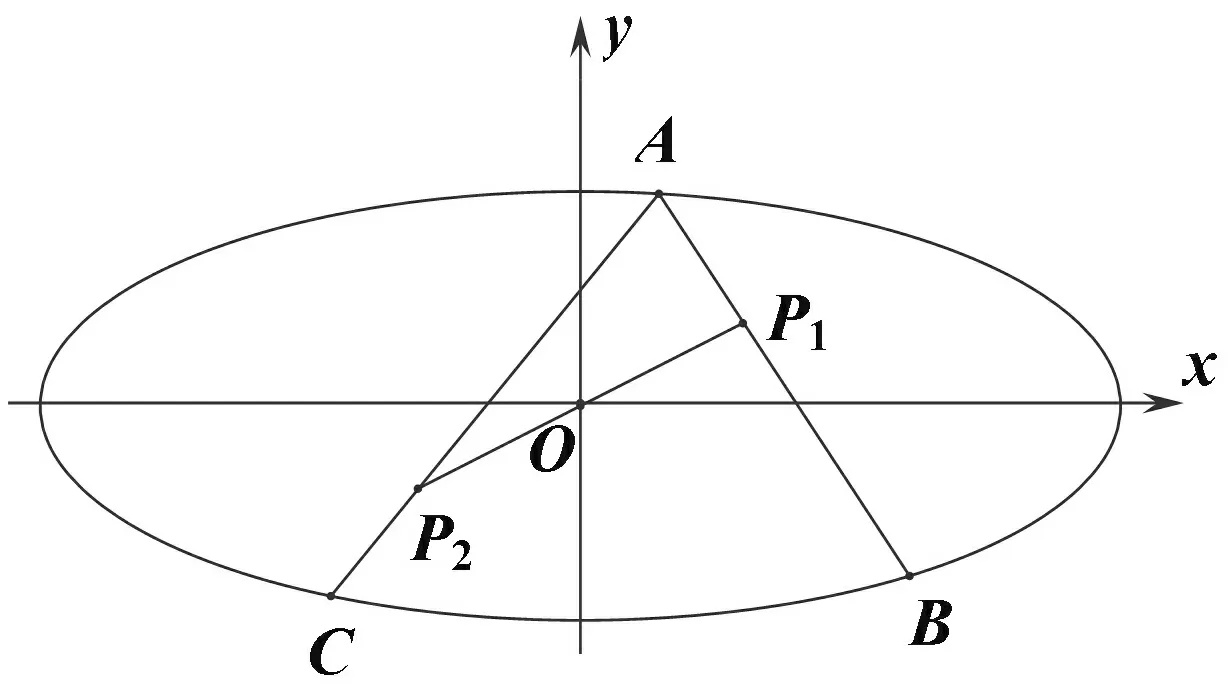
图1
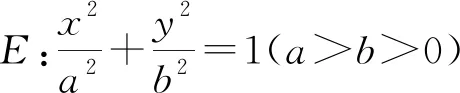

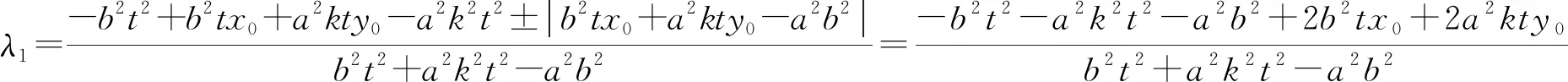
若λ1=-1,则x0=x1,y0=y1,即A,B重合,这不可能.故λ1≠-1.同理可得
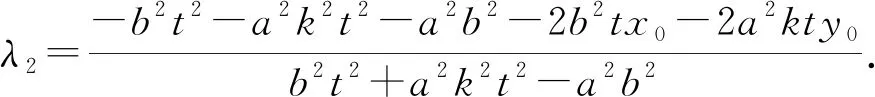
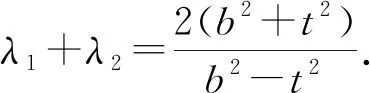
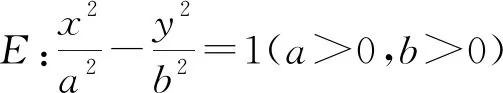
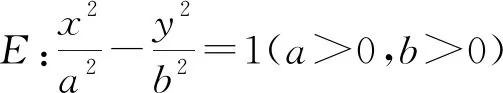
遗憾的是,在抛物线上,没有发现一套与上面的结论完全类似的完整的结论.但是,我们仍然发现一个与性质1相仿的结论.
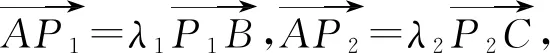
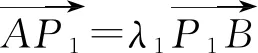
3 性质1的一个别证
通性通法证明性质1,好处在于容易理解,不足之处是计算实在繁琐.受文[2]给出的一种方法的启发,下面将利用圆锥曲线极点与极线的性质给出性质1的另一证明.首先,我们给出一些预备知识.
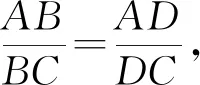

图2
引理1 如图2,D是圆锥曲线Γ外一点,l是Γ关于D的极线,过D的任意直线交于A,B,交l于C,则A,C,B,D是调和点列.
引理2 若点F关于圆锥曲线Γ的极线为l,则l上任意的点关于Γ的极线必过F.
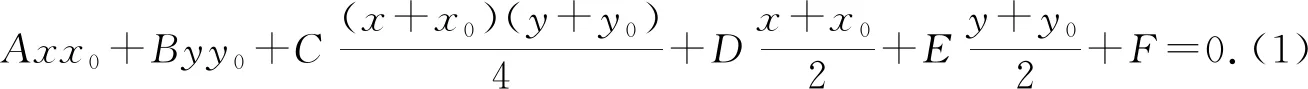
任取l上一点K(x1,y1),则x1,y1满足(1)式.从而,x0,y0满足点K关于Γ的极线的方程,即F在K关于Γ的极线上.
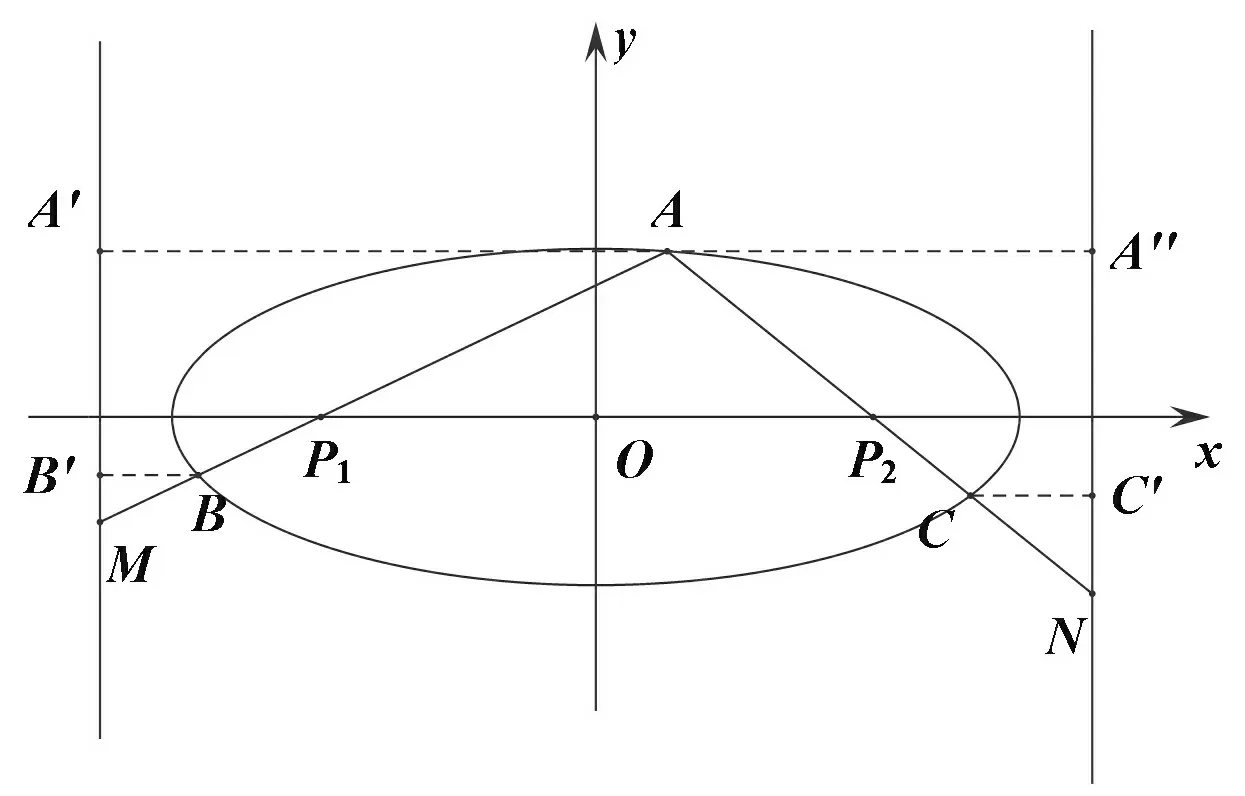
图3
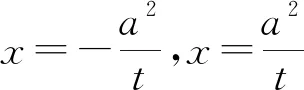
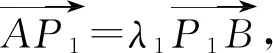
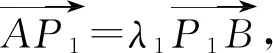
同理可得,λ2x2=λ2t+t-x0.(4)
定值、定点问题在圆锥曲线的考察中出现频率较高的一类问题.在平时的教学中,我们应该践行“为核心素养而教”的教育理念,引导学生积极探究,挖掘问题背后的一般规律,激发学生的学习兴趣.
猜你喜欢
中学生数理化(高中版.高二数学)(2022年1期)2022-04-26
新世纪智能(教师)(2021年2期)2021-11-05
疯狂英语·新悦读(2019年10期)2019-12-13
家庭医药·快乐养生(2019年7期)2019-07-25
发明与创新·中学生(2019年1期)2019-03-23
电子制作(2018年10期)2018-08-04
电子制作(2018年12期)2018-08-01
理科考试研究·高中(2017年8期)2018-03-06
广东教育·高中(2017年10期)2017-11-07
读者·校园版(2015年7期)2015-05-14

