几个重要不等式及不等式证明方法探析

吕 军 库福立 阿布力米提·孜克力亚*

（新疆农业大学数理学院 新疆·乌鲁木齐 830052）

0 引言

不等式是高等数学中的一个重要研究内容，它反映了某些变量之间的某种“大小”关系。其在物理学、数值分析、工程技术等众多领域有着广泛的应用，特别是一些重要的不等式，例如：柯西不等式、闵可夫斯基不等式、贝努利不等式等一直都是很多学者研究的热点问题。而在高等数学中，我们的着重点是不等式的证明，不等式的证明是高数中的一种常见的题型，同时也是考研中经常会出现的一种题型。由于其证明方法较多、较复杂，学生们往往感到不知从何入手，因此研究其证明方法就显得尤为重要。本文的重点就是对其证明方法进行了归纳解析，其目的就是让学生能更多的掌握证明方法，进一步开拓解题思路，达到学以致用的目的。

1 重要不等式

2 不等式证明方法

2.1 引入参数变量法

2.2 利用微分中值定理

2.3 利用函数的单调性

该方法一般适用于某区间上的函数不等式的证明，而对于数值不等式通常需要通过辅助函数的构造来完成不等式的证明。利用单调性证明不等式的步骤如下：

2.4 利用函数的极值和最值

该方法也是适用于在某个区间上证明不等式，证明的方法和步骤与利用单调性的类似，区别在于所作的辅助函数比较的不是函数在端点处的函数值，而是极值与最值。

2.5 利用函数图形的凹凸性

2.6 利用泰勒展开式

此方法一般适用于题设中已给出函数具有二阶及其以上可导，并且最高阶导数的上下界是已知的条件下。其证明的步骤如下：

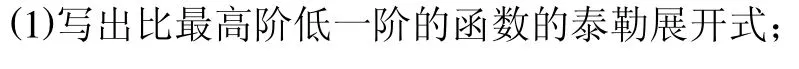
2.7 利用重要不等式

2.8 利用幂级数展开式

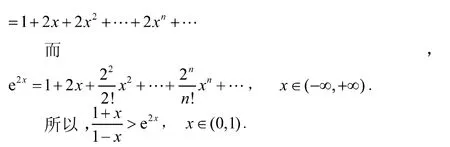
3 结束语

通过以上对不等式的归纳总结可以看出，不等式证明的题型多种多样，其证明的方法也是各不相同，难度较大。因此就需要学生在学习过程中能具体问题具体分析，学会灵活多变，举一反三，深刻掌握每种证明方法的内在特征，这样才能较有效的解决各类不同类型的不等式证明问题。