深光晶格势阱中凝聚体的扭结包络隙孤子
杨如曙,杨江河
( 湖南文理学院计算机与电气工程学院,常德 415000)
1 引 言
玻色-爱因斯坦凝聚体( BEC) 被局陷在两束耦合激光驻波形成的光晶格势阱中的物性研究受到了广泛地关注,主要是研究局陷于光晶格势阱中BEC 的性质可为原子激光和原子干涉仪等具体应用提供更加广泛的市场[1-14].值得一提的是,Eiermann 等[11]在局陷于光晶格势阱的BEC 体系中实验观察到了一种隙孤子( gap soliton) ,且这一隙孤子一直钉扎于光晶格的某一具体位置既不发生衰减也不会产生形状等方面的改变,它为一典型的空间局域化的隙孤子( Spatially Localized Gap Soliton).由于局陷于光晶格势阱中的BEC 类似于局陷于晶格中的电子,因而人们常采用紧束缚近似[15,16],正交完备Wannier 函数法[17],有效质量法[18],平面波方法[19]等一些固体物理学的近似方法来研究局陷于光晶格势阱中的BEC 的动力学行为.已有研究表明,对于局陷于光晶格势阱深度较浅的正s -波散射长度的BEC 体系中会形成亮隙孤子; 而对于负s -波散射长度的BEC 体系产生暗隙孤子[15-31].尽管固体物理学中的这系列方法为研究局陷于浅光晶格势阱中的BEC 动力学提供了便利和可行,然而当BEC 局陷于深光晶格势阱时,则势阱与势阱之间的BEC 隧穿效应会明显增强,因而此时固体物理学的这些近似方法并不能完整地描述BEC 中的动力学性质.所以,有必要发展新的方法来研究光晶格势阱中BEC 的动力学特性[20].
事实上,局陷BEC 的光晶格势阱的深度越深,则光晶格势阱内的凝聚体被束缚得越紧,而光晶格势阱之间的凝聚体隧穿效应会明显增强[3].当局陷凝聚体的光晶格势阱的深度相当深时,实验上观察到自陷隙孤子( self-trapping gap soliton)[12,13].特别是2020 年,Oldziejewski 等[32]发现当BEC 局陷于一个相当深的光晶格势阱内,系统不仅会出现亮隙孤子而且还会显示出一些强相关的量子液滴( strongly correlated quantum droplets).这意味当BEC 局陷于相当深的光晶格势阱系统中可能会产生其他形式的隙孤子.进一步研究局陷于深光晶格势阱中的BEC 的孤子,对于提高原子钟的测量精度具有重要意义[33].
由于局陷于光晶格势阱中的BEC 类似于局陷于晶格中的电子,体系的动力学行为可借用固体物理学中的紧束缚近似方法来描述.与此同时,局陷在各个光晶格势阱中的凝聚体是被各个势阱所隔开,因而可采用准离散多重尺度方法来描述其中的动力学行为.因此,本文我们发展准离散多重尺度法结合紧束缚近似研究光晶格势阱中BEC 的动力学行为.结果在系统的能隙中发现一种新颖内在的局域模: 扭结包络隙孤子,且其幅度可通过形成光晶格势阱的晶格常数和势阱深度这两个重要物理参数进行操控.
2 模型和孤子的稳定性分析
实验上,局陷BEC 的光晶格势阱是由两束相向传播的激光束之间的干涉所形成[11-14].光晶格势阱的晶格常数是通过两束交叉耦合激光束之间的夹角来调控,其变化范围在0.4 -1.6 μm 之间[11,12].光晶格势阱深度则与交叉耦合激光束的光强成正比,变化范围在0 和Emax0=20Erec之间,其中Erec=π2ħ2/(2md2) ( 式中m 是凝聚体的冷原子质量,d 代表光晶格势阱的晶格常数) 为晶格反冲能量( the lattice recoil energy)[11,12].理论上,BEC 所局陷的光晶格势阱V 通常由两部分组成[15,16],即V=Vh+Vp,其第一项为谐振外部势阱式中ωX和ωR分别是谐振外部势阱的轴向和径向谐振频率,第二项为周期外部势阱,Vp( X)=Vp( X + λ) ,其中λ 为形成光晶格势阱的激光束波长.相应地,局陷BEC 的周期性光晶格势阱可表示为[15,16]
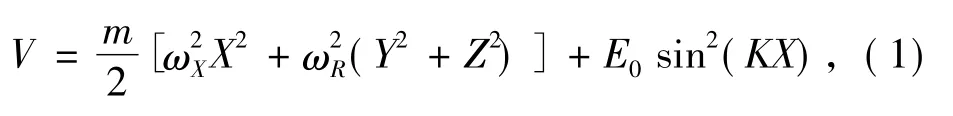
其中,E0和K=2π/λ 分别是BEC 所局陷的外部光晶格势阱的势阱深度和所形成光晶格势阱的激光波数.根据现有的实验条件[11],我们在此考虑一维烟型的87Rb 原子凝聚体(87Rb 原子质量是14×10-25kg,其s-波散射长度为5.3nm) 所局陷的光晶格势阱的轴向谐振频率为ωX=2π ×0.5 Hz,而其径向谐振频率是ωR=2π ×85 Hz 的外部光晶格势阱,并设每个光晶格势阱约承载900 个87Rb原子凝聚体.由于ωX/ωR≈0.006 ≪1 ,因而BEC 所局陷的外部光晶格势阱可看作为准一维的光晶格势阱.
正如文献[21,34]所讨论,描述局陷于光晶格势阱中的一维BEC 动力学行为的无量纲Gross-Pitaevskii( GP) 方程是
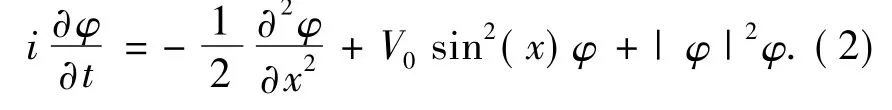
为了能获得局陷于光晶格外部势阱中的BEC形成孤子的性质,我们先分析该体系形成孤子的稳定性条件.为此,体系的波函数可定义为[18]
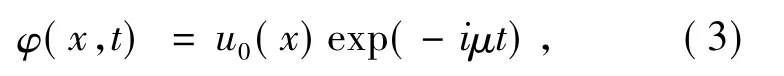
其中,μ 是系统的化学势,u0( x) 为描述体系孤子形状的实函数.将方程( 3) 代入GP 方程( 2) ,可得到
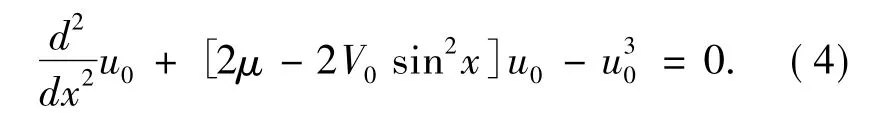
在线性情况下,方程(4) 正是Hill 方程[35]
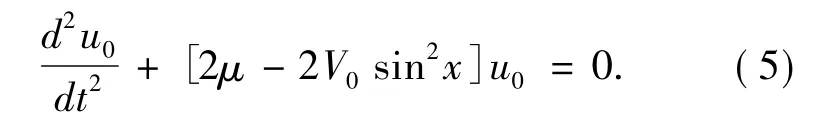
根据Floquet -Bloch 定理,描述体系孤子形状的函数u0( x) 按照光晶格势阱周期函数Vk( x) 展开为u0( x)=Vk( x) exp( ikx) ( 其中k 为波矢).由固体物理学中的平面波方法可知[19],晶格与凝聚体相互作用下的μ - k 的能带结构对BEC 的线性性质起着决定性的作用.为此,图1 示出了局陷于光晶格势阱的势阱深度是V0=10 且晶格常数为d=1μm 的体系能带结构图.

图1 势阱深度V0=10 和晶格常数d=1 μm 情况下体系的能带结构图.曲线I -V 分别对应于体系的前五个能带.Fig.1 The band structure for V0=10 and d=1 μm Curves I-V correspond to the first five bands,respectively.
从能带结构图1 可看出,对于处于能带中的化学势μ,方程( 5) 具备线性的周期性解,且这些能带结构的线性周期性可以判定局陷于光晶格势阱中BEC 形成孤子的稳定性条件[7,18].正如文献[18]所得,局陷于光晶格势阱能隙中的凝聚体的孤子是稳定的,而局陷于能带内的凝聚体的孤子由于振动行为变得不稳定.这一结果也可从文献[7,9]获得.因此,我们下面仅讨论局陷于光晶格势阱中凝聚体能隙中的孤子行为.
既然局陷于光晶格势阱中的BEC 类似于局陷于晶格中的电子,体系的动力学行为可借用固体物理学中的紧束缚近似方法来描述.在紧束缚近似下,体系的波函数可写作[15,16]
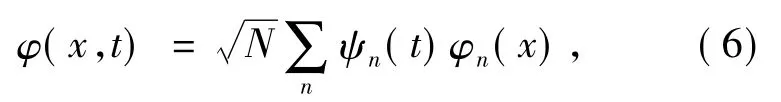
其中,N 是凝聚体的原子数,φn( x) 是处于光晶格势阱中心的最低位置的与空间相关的实函数,ψn( t) 为第n 个光晶格势阱的凝聚体波函数,且其可与相邻光晶格势阱的波函数ψn±1发生弱耦合作用.
将紧束缚近似波函数方程( 6) 代入GP 方程(2) 并对整个空间积分,就可得到离散的非线性Schrödinger 方程

一般情况下的非线性Schrödinger 方程( 7) 是不可积的,然而当凝聚体局陷于光晶格势阱中时,每个势阱中的凝聚体会局陷于各自的势阱中,从而凝聚体被各自势阱所隔开,因此我们可引入准离散多重尺度法[36,37]来研究体系凝聚体的动力学行为,可设
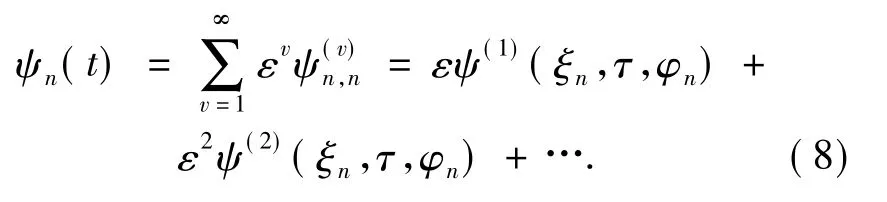
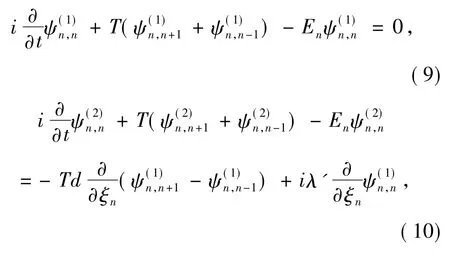
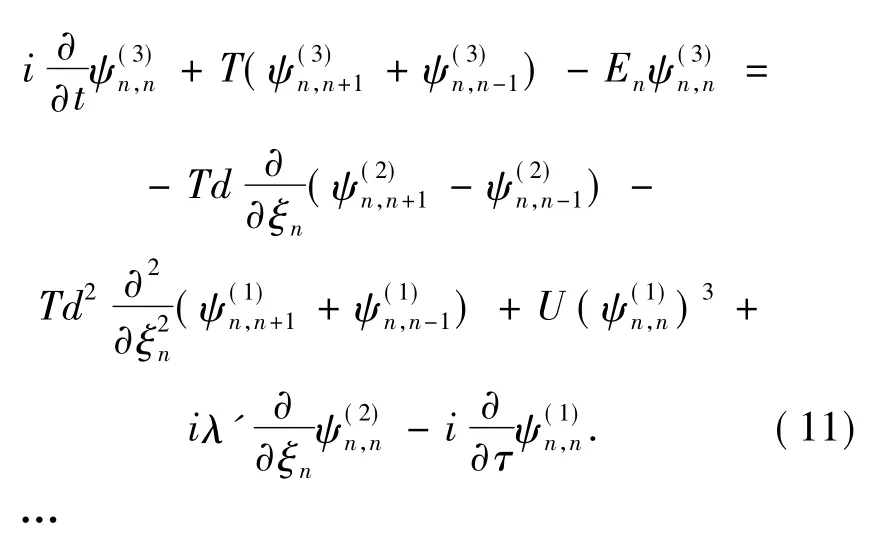
基于离散波近似,可设
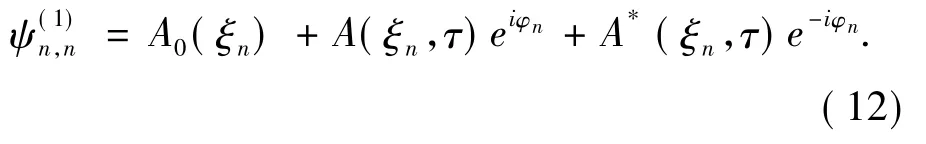
将方程(12) 代入方程(9) 中,可得En=2T.相应的系统的线性色散关系为ω=2T[1 -cos( k′d) ].其群速度是
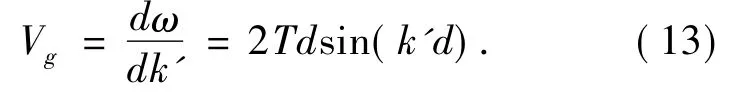
随后,将方程(12) 代入方程(10) 中,可得
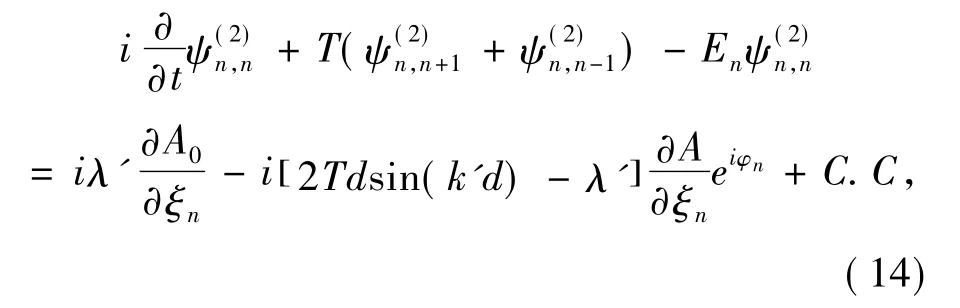
其中C.C 代表共轭复数.方程(14) 右边第二项是久期项,消去久期项后得到λ′=2Tdsin( k′d)=Vg.从而得出待定参数λ′ 正是晶格格波的群速度.目前实验上[11-14]形成光晶格势阱的激光驻波的波矢是k′=2π/λ,且驻波之间相邻波腹之间的距离( 即光晶格的晶格常数) 是d=π/2,因此局陷于光晶格势阱中的凝聚体的孤子是局域在初始位置并不传播.
从而,方程(14) 式的解具有如下形式
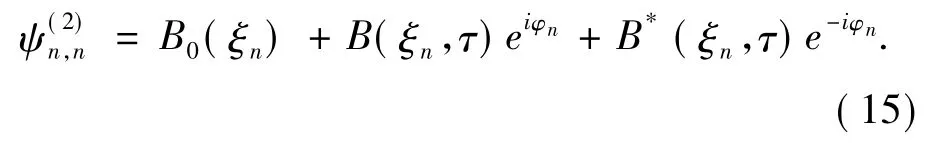
当仅仅考虑幅度最低阶A 的关系时,可设B0( ξn)=0.从而,将方程(15) 代入方程(14) ,然后通过求解此线性微分方程,有
随后,将方程(12) 和(15) 代入方程(11) ,则方程(11) 可化为
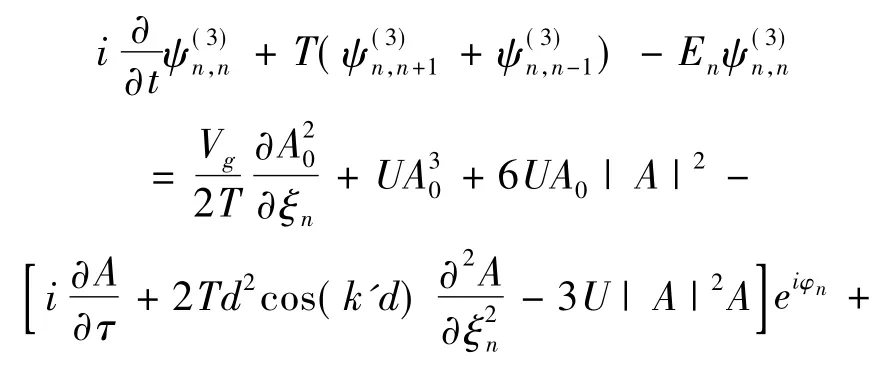
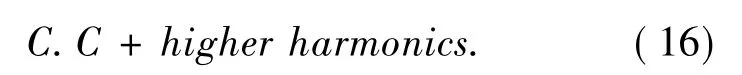
类似地,消除方程(16) 右边的久期项,可得
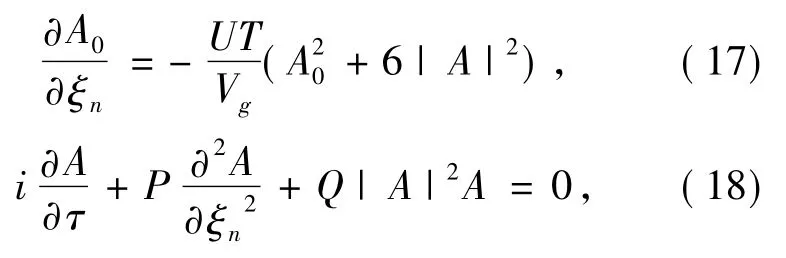
式中,P=2Td2cos( k′d) ,Q=-3U.利用初始变换关系A0=ψ0/ε,A=ψ/ε,ξn=ε( nd -Vgt)=εXn和τ=ε2t,方程(17) 和(18) 分别被化为
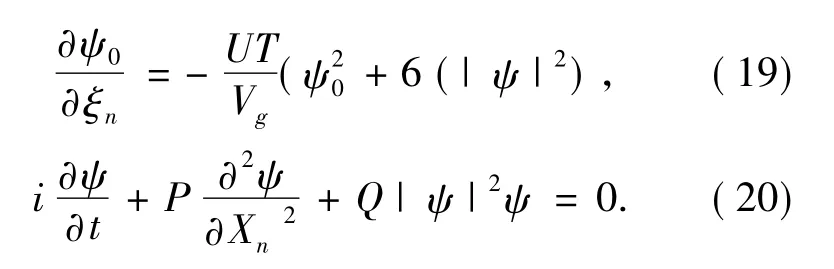
显然,只要求出方程(19) 和(20) 的解,就可以获得局陷于光晶格势阱的BEC 的孤子动力学行为.
3 光晶格势阱中BEC 孤子性质
在此,我们选取正s -波散射长度的87Rb 原子凝聚体[11]局陷于光晶格势阱的非线性动力学性质作为一个典型事例来说明光晶格势阱中BEC 的孤子性质.由方程(18) 可得物理参数U >0 ,T <0 ; 且在这情况下cos( k′d) >0.相应地,由方程(18) 所得出P 和Q 的乘积表达式是PQ=-6UTd2cos( ~kd) ,因此,对于正s-波散射长度的87Rb 原子凝聚体局陷于光晶格势阱中后,PQ >0.相应地非线性Schrödinger 方程( 20) 的单孤子解为[38]
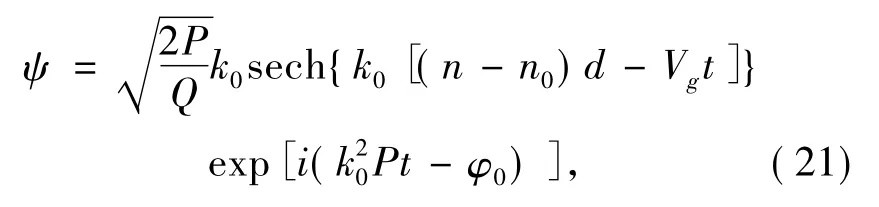
式中,积分常数n0代表系统形成孤子后孤子的初始中心位置,积分常数k0和φ0分别表示体系形成孤子后孤子的初始幅度和初始相位.
随后,分析方程(19) 右边两项的数值大小发现,其第一项总是比第二项小得多,这主要是因为从方程(12) 可得出物理参数和| ψ|2属于同一数量级的参数.相应地,将方程(21) 代入方程(19) 然后积分可得ψ0的近似解为
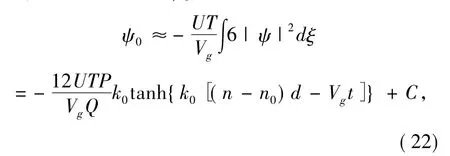
式中C 为一任意积分常数.因此,局陷于光晶格势阱中的第n 个光晶格势阱的波函数是
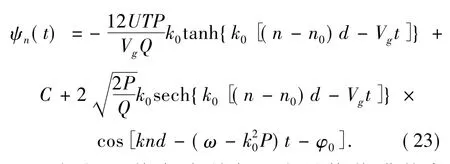
根据目前实验所实现光晶格势阱的条件[11,12],可选择的物理参数分别为d=0.11,U=0.2,En=- 1.0,k′=5.0/d,C=1.0,k0=1.0,n0=50,t=0 和φ0=0.当BEC 所局陷的光晶格势阱较浅时,势阱之间的BEC 所发生的隧穿效应相当弱[3],图2 示出了T=0 时凝聚体的概率密度分布.从图可看出,局陷于浅光晶格势阱中的正s 波散射长度BEC 在能隙中所观察到的是对称的包络隙孤子,且包络隙孤子的局陷中心位置为n=n0处.这是一种典型的内在局域模,局域在初始位置后进而扰动最终演化为一个包络孤子和一个色散的高斯尾巴.这是由于BEC 所局陷的光晶格势阱较浅,光晶格势阱的势阱深度较小,相邻光晶格势阱中的BEC 隧穿效应相当弱,系统所能观察到的是一种稳定的对称包络隙孤子.
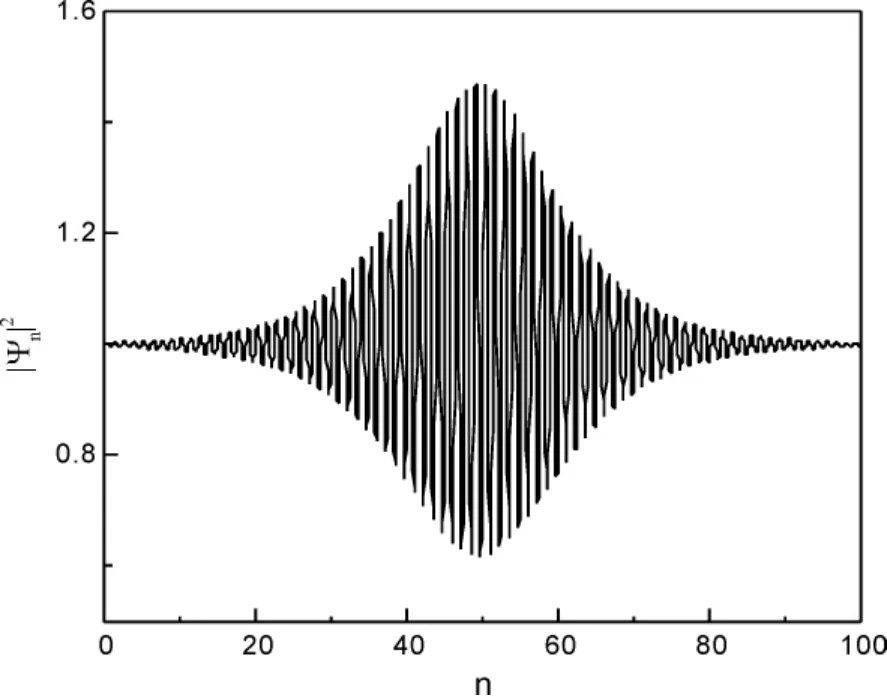
图2 无隧穿( T=0) 情况下,局陷于光晶格中凝聚体的概率密度分布.图中所使用的其他无量纲的物理参数分别是: d=0.11,U=0.2,En=-1.0,k=5.0/d,C=1.0,k=1.0,n0=50,t=0,φ=0.Fig.2 The density distribution of the condensate trapped in optical lattices with the T=0.The parameters used are d=0.11,U=0.2,En=-1.0,k=5.0/d,C=1.0,k=1.0,n0=50,t=0,and φ=0.All parameters used are in dimensionless units.
当BEC 所局陷的光晶格势阱较深时,相邻光晶格势阱中的BEC 的隧穿效应就会相应地增强[3].因此,随后探讨光晶格势阱的晶格常数和势阱深度对局陷于光晶格势阱中的凝聚体隙孤子的影响.为此,我们数值模拟出不同的隧穿强度T 和不同的晶格常数d 下,局陷于光晶格势阱中的凝聚体的概率密度分布,如图3 所示.从图3( a) 可看出,当BEC 所局陷的光晶格势阱较深,且相邻光晶格势阱中的凝聚体发生隧穿的强度为T=-0.5 时,能在局陷于光晶格势阱的凝聚体中的能隙中观察一个包络隙孤子和一个扭结孤子叠加而成的新型的扭结包络隙孤子.这说明局陷于深光晶格势阱中的BEC 能在其能隙中观察一种新型的非线性元激发: 扭结包络隙孤子; 且这种典型的非线性元激发是一种典型的内在局域模.
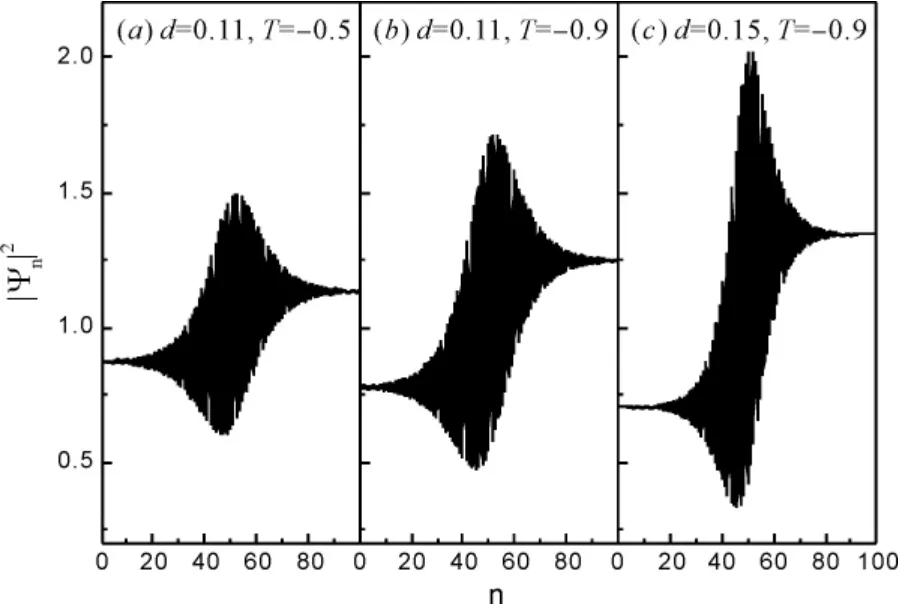
图3 不同晶格常数和隧穿强度( a) d=0.11,T=-0.5,( b) d=0.11,T=-0.9,和( c) d=0.15,T=-0.9,情况下,凝聚体的概率密度分布.图中所使用的其他物理参数与图2 一致.Fig.3 The density distribution of the condensate with different parameters ( a) d=0.11,T=-0.5,( b) d=0.11,T=-0.9,and ( c) ( c) d=0.15,T=-0.9.The other parameters used are the same as those of figure 2.
随着局陷于BEC 的光晶格势阱深度的进一步增加,从方程( 7) 可得出相邻光晶格势阱中的BEC 发生的隧穿强度会作相应地增加.因此在图3( b) 中我们保持其他物理参量均不变,仅仅使相邻之间的隧穿强度变化为T=-0.9 情况下的凝聚体局陷于深光晶格势阱中的凝聚体概率密度的分布.通过对比图3( b) 和( a) 发现,局陷于深光晶格势阱中的BEC 在其能隙中所观察到的隙孤子仍然为扭结包络隙孤子,但扭结包络隙孤子的幅度随着所局陷BEC 的光晶格势阱深度的增加有所增加.最后,我们分析局限于BEC 的光晶格势阱的晶格常数对体系隙孤子的影响,因而在图3( c) 中我们保持其他物理参量不变,仅仅使局陷BEC 的光晶格势阱的晶格常数增加到0.15,可看到扭结包络隙孤子的幅度随着所局陷BEC 的光晶格势阱的晶格常数的增加而进一步增加.
基于上述理论研究现象,我们可提出一套调控局陷于光晶格外部势阱中的BEC 体系的隙孤子的幅度的实验方案为: 首先,让两束激光光强较弱的相向传播的光束产生干涉现象构成一个光晶格外部势阱[11-14]; 随后将87Rb 原子凝聚体注入上述光晶格外部势阱中,结果会在整个装置中观察到一对称的局域包络隙孤子; 然后,将形成光晶格势阱的两束激光的光强增加,人们会观察到原来体系所形成的局域包络隙孤子转变为扭结包络隙孤子; 最后,进一步增加形成光晶格势阱的两束激光的光强,会发现扭结包络隙孤子的幅度增加.当然进一步使构成光晶格外部势阱的两束激光之间的夹角增加,也会发现扭结包络隙孤子的幅度将会进一步增加.
4 结 论
总之,通过发展准离散多重尺度方法结合紧束缚近似,我们解析地研究了局陷于光晶格势阱的BEC 的孤子动力学行为.首先,我们探讨了局陷于光晶格势阱中的BEC 系统形成孤子的线性范畴,结果发现局陷在体系能隙中的孤子是稳定的,而处于体系能带中的孤子会出现振动行为而不稳定.与此同时,我们得到系统能隙中所形成的孤子是局陷在初始位置并不传播.随后,我们将87Rb原子凝聚体注入光晶格势阱深度较浅的光晶格外部势阱中,体系会产生稳定的对称的包络隙孤子.当BEC 所局陷的光晶格外部势阱的势阱深度增加时,体系会产生一种新型的非线性元激发:扭结包络隙孤子.最后,通过数值计算发现体系的扭结包络隙孤子的幅度可通过BEC 所局陷的光晶格势阱的晶格常数和势阱深度来调控.相应地,我们提出了一套实验方案去操控局陷于光晶格势阱中BEC 隙孤子幅度的方法是通过增加构成光晶格外部势阱的两束激光激光强度和( 或) 使这两束激光之间的夹角增加来增加扭结包络隙孤子的幅度.

