基于自动控制系统稳定性的几种判定分析方法

忽建蕊

云南现代职业技术学院，中国·云南 楚雄 675000

1 引言

稳定性是控制系统正常工作的首要条件，也是控制系统的一个重要性能指标。一个控制系统在实际运行过程中，总会受到外部和内部一些因素的干扰，如负载的变化，电源的波动。系统参数的飘移，环境条件的改变等。一个稳定的系统，受到扰动作用后会偏离原来的平衡状态，但扰动消失后，随着时间的推移能够逐渐恢复到原来的平衡状态。一个不稳定的系统，会在任何微小的扰动作用下偏离原有的状态，并随时间的推移而发散，也就是说系统不会依靠自身的调节达到稳定状态。

系统稳定性是扰动消失后系统自身的一种恢复能力，是系统的一种固有特性，它只取决于系统的结构和参数，而与初始条件及外作用无关。但系统中的参数或结构究竟应取怎样的数值或结构才能满足系统稳定性的要求，仅用定性分析是解决不了的，这时可以采用数学方法来分析系统的稳定性，即直接法。通过特征根的实部正负来判定系统的稳定性[1]。

2 直接法判定

假设系统的输入量只有扰动作用D(t)，扰动作用下的输出为C(t)，则系统的微分方程的一般式为：

根据稳定性概念可知，研究系统稳定性，就是研究系统在扰动消失以后的运动情况。因而，可以从研究上式微分方程的等号右边为零时的情况入手，即研究上式微分方程的齐次方程：

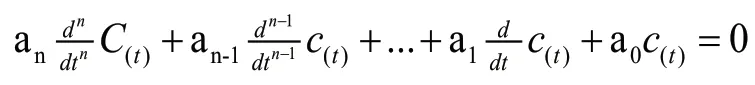
该齐次方程的解就是扰动作用过后系统的运动过程。因此，若此解是收敛的，则该系统便是稳定的；若此解是发散的，则该系统便是不稳定的。

由高等数学可知，解齐次微分方程，首先应求解它的特征方程，即：

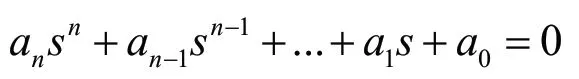
当求得了特征方程的根s1,s2,...,sn时，就得到齐次微分方程解的一般式，即：

式中，c1,c2,...,cn是积分常数。特征方程的根可能是实根，也可能是复根。

①如果特征方程有一个实根s=a，则齐次微分方程的解为c(t)=ceat，它表示扰动消失以后的运动过程是指数曲线形式的非周期性变化过程。由高等数学可知，若a 为负数，则当t→∞时，c(t)→ 0，说明系统的运动是衰减的，并最终返回原平衡状态，即系统是稳定的。若 a 为正数，则当t→∞时c(t)→∞，说明系统的运动是发散的，不能返回原平衡状态，即系统是不稳定的。

②如果特征方程有一对复数根S=a±jw，则齐次微分方程的解为：

它表示系统在扰动消失以后的运动过程是一个周期性振荡过程。此时，若a 是负数，则当t→∞时c(t)→∞是个衰减振荡过程，即系统是稳定的。若a是正数，则当t→∞时c(t)→∞，是个发散振荡过程，即系统是不稳定的。

3 间接法判定

3.1 利用代数稳定性判据判定系统稳定性

系统稳定性的代数判据很多，其中劳斯——赫尔维茨稳定性判据是一种非常快捷方便的代数判定方式，它是一种根据闭环特征方程的系数来确定系统稳定性的代数方法。

若已知线性系统的特征方程为：

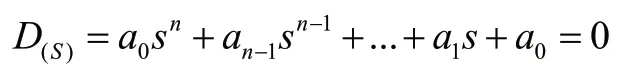
则由特征方程的系数可排成下列的行列式。此行列式的特点是：第一行为第二项，第四项等偶数项的系数，第二行则为第一项，第三项等奇数项的系数；第三行、四行则重复第一行，第二行的排列，但向右移动一列，前一列则以0数代替；以下各行以此类推，换句话说，主对角线上的元素为a n−1,an−2,...a1,a0，其他列上的元素为从上至下升幂排列，不足项用0 填补。式中， Δ1,Δ2,Δ3,...Δn−1,代表各子行列式。

劳斯——赫尔维茨稳定性判据的结论为：系统稳定的充分且必要的条件是：

①系统的特征方程的各项系数a n,an−1,...a1,a0，均为正值。

②主行列式Δn和各子行列式Δ1, Δ2,Δ3,...Δn−1,的值均大于零。

3.2 利用频域判据判定系统稳定性

3.2.1 根据系统的开环奈奎斯特曲线判定稳定性

理论上可以证明，系统的开环频率特性与闭环稳定性之间存在某种确切的相互关系[2]。奈奎斯特稳定判据就是根据这种关系，通过开环奈奎斯特曲线来判别系统的闭环稳定性的。

假设n 阶系统的开环传递函数为：

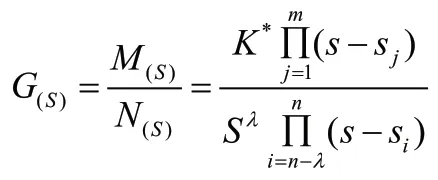
式中，K*为根轨迹增益；Sj是M(S)=0 的根，称为开环零点；Si是N(S)=0 的根，称为开环极点；λ是开环传递函数中所含纯积分环节的个数，可能有，也可能不止一个。

设从N(S)=0 解得的全部开环极点（也叫开环特征根）中有P 个位于S 平面右半部（正实部极点，也称开环不稳定根）。

①若开环系统稳定（P=0），则闭环系统稳定的充分必要条件为开环奈奎斯特曲线不包围（-1，j0）点，否则闭环系统不稳定。

②若开环系统不稳定（P ≠0），则闭环系统稳定的充分必要条件是开环奈奎斯特曲线逆时针包围（-1，j0）点的圈数K=P/2，否则闭环系统不稳定。规定：K=K+−K−，开环奈奎斯特曲线在（-1，j0）点左边的负实轴上，由上向下穿越负实轴的次数为K+，由下向上穿越负实轴的次数为K-。

③无论系统开环是否稳定，若开环奈奎斯特曲线穿越（-1，j0）点，则闭环系统属于临界稳定。

3.2.2 根据系统的半对数坐标图（Bode 图）判定系统的稳定性

如果系统有P 个开环右极点，则该系统闭环稳定的充分必要条件是当W=0 →∞时，在半对数坐标图的幅频特性L(W)＞0dB的频段内，对数相频特性曲线穿越-180°线的正负穿越次数之差应等于P/2，即K=K+-K-=P/2，否则闭环不稳定。规定：半对数坐标图的对数相频曲线从下向上穿越-180°线的次数为正穿越次数，用K+表示；从上向下穿越的次数为负穿越次数，用K-表示。如果λ ≠0，需要从对数相频曲线的起点向0°线方向补画一段角度等于λg（-π/2）的虚线。

4 MATLAB 工具软件辅助判定

以上各种判定方法并不复杂难懂，适用于中低阶系统，但对于高阶系统求解高阶方程和描画各种图形时比较烦琐。如果采用MATLAB 工具软件来辅助判定稳定性，一切就变得简单容易起来。下面介绍MATLAB 在系统稳定性分析中的应用方法[3]。

4.1 根据闭环极点（特征根）判定系统的稳定性

在MATLAB中，可用roots函数直接求取系统的特征根，其调用格式是：roots（C）。

式中C 为多项式系数向量，由高阶向低阶顺序列写，0 系数也不可省略。若多项式为：D(X)=C0X n+C1Xn−1+ ...+C n−1X+Cn，其中C=[C0,C1,C2,...C n−1,Cn]，那么根据程序执行结果中特征根的实部的正负即可判定系统的稳定性。

4.2 利用稳定裕度判定系统稳定性

利用Margin()函数可以计算给定线性系统的相位裕度和幅值裕度。该函数的调用格式是：[Gm,Pm,Wg,Wc]=margin(g)。式中，[Gm,Wg]为幅值裕度及对应频率；[Pm，Wc]为相位裕度及对应频率，g 是给定系统模型。很显然，根据稳定裕度的定义，对于稳定系统，必然存在Gm＞1，Pm＞0°；对于不稳定系统，则Gm＜1，Pm＜0°。

5 结语

工程上对系统性能进行分析的主要内容是稳定性分析、稳态性能分析和动态性能分析。其中，最重要的性能是稳定性，这是因为任何系统要想能够正常工作，首先它必须是稳定的。在判定稳定性的方法中直接法是通过求解特征根，利用特征根的实部正负进行判定，这种方法较适用于中低阶系统，对于高阶系统求解特征根过程烦琐；间接法通过代数判据和频域判据进行判定，其中频域判据应用方便、直观，而且从图形上还可以直观地看出系统的稳定程度，即系统离“稳定边界”的“距离”。MATLAB 工具软件辅助判定法不仅可以减轻系统分析的工作量和任务难度，而且大大提高了工作效率和分析精度，是一种简单实用的有效方法。