可转换债券的价值评估——二叉树期权模型的应用

■崔 劲 殷 霞 豁秋菊

（北京天健兴业资产评估有限公司，北京100039）

一、引言

可转换债券（Convertible Bonds）是一种可以根据约定条件在适当时间转换成股票的公司债券，简称可转债。可转债赋予债券持有人在规定的期限内、依照约定的价格将其所持债券转换为公司股票的权利，这种权利嵌入在固定收益债券中，因此可转债有时也被称为含权债券。

根据《企业会计准则第22 号——金融工具确认和计量》以及《企业会计准则第37 号——金融工具列报》的规定，可转债属于同时包含金融负债成分和权益工具成分的复合金融工具，应确认为发行公司的一项金融负债并以公允价值进行计量。随着我国资本市场的发展，可转债已逐渐成为上市公司普遍使用的融资方式，存量规模和债券数量都呈现较快增长态势。截至2021年11月，我国上市公司可转债存量规模突破6 400 亿元，债券数量达到410 只，同比增长分别为20%和9%左右，可转债已经成为资本市场的重要交易品种，受到投资者和上市公司的高度重视与广泛欢迎（如图1所示）。

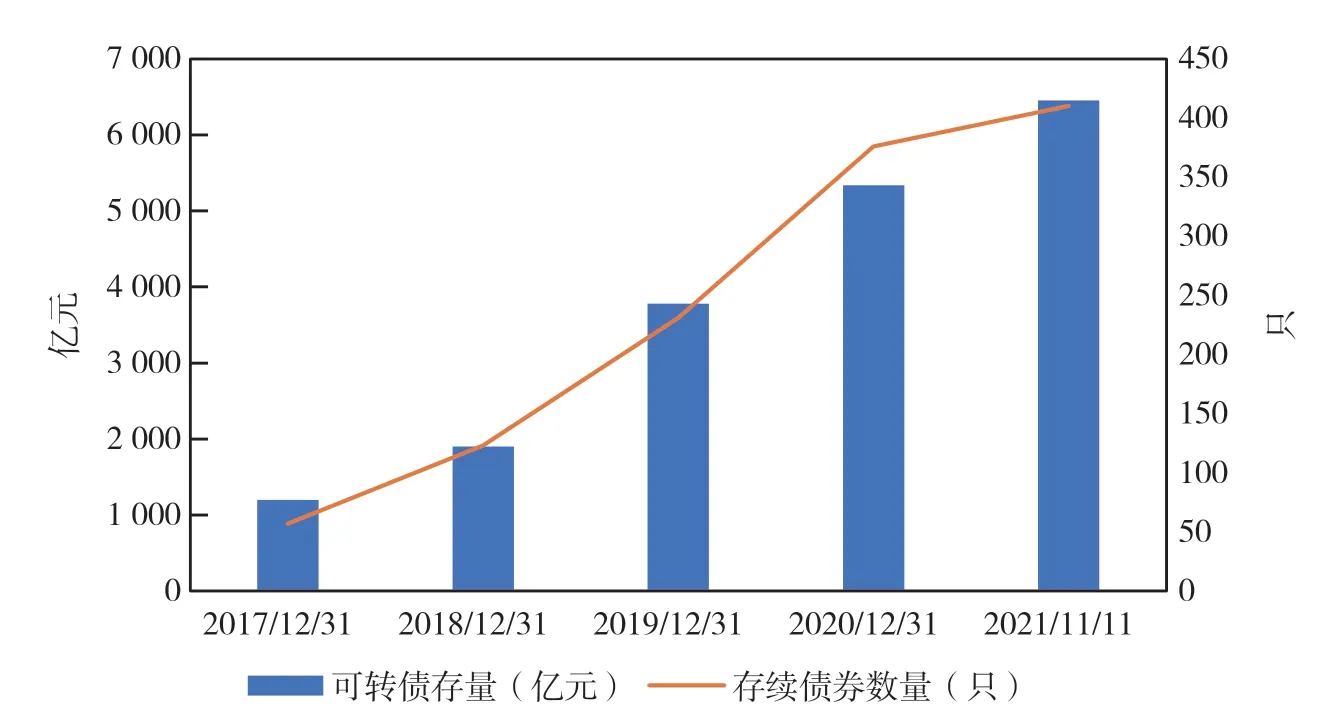
图1 我国上市公司可转债存量规模及数量

然而，由于可转债在发行时除了设置转股权，还会附加赎回权、回售权等多项权利，使得可转债同时具有债券、股权和期权的属性，导致可转债在合理定价方面存在诸多困难，这无疑将影响拥有可转债公司的企业价值的恰当估值及相关会计计量的公允性和合理性，对上市公司债务融资以及可转债市场的持续健康发展产生不利影响。

在资本市场实务中，可转债交易市场价格波动激烈，仅在2020年，就发生了横河转债两天翻倍，振幅高达138%，让市场知道可转债“有利可图”的案例；也出现了泰晶转债一天价格接近腰斩，跌幅达47.68%，要市场领略了可转债的“无情”，也见证了赎回权的可怕“威力”。可转债价格看似“神秘莫测”，吸引了资本市场的广泛关注，其定价研究迫在眉睫。

本文将对可转债的价值影响因素以及定价模型进行深入剖析，为资产评估服务资本市场及会计计量提供理论指导和实践参考。

二、可转债的价值影响因素

可转债是固定收益债券与嵌入期权的混合产品，因此其价值影响因素可分为债券价值影响因素和嵌入期权价值影响因素两大类。

（一）债券价值影响因素

债券的基本特征是债券发行人承诺在固定期限内定期（每年、每半年、每季度等）向债券持有人按照固定利率或浮动利率支付利息，其基本价值要素包括票面价值、息票利率、存续期限和违约风险等。

票面价值也称面值（Face Value），是指标明每份可转债的价值，也是每份可转债持有至到期能够获得的本金数额。国内发行的可转债面值一般都默认为100 元。可转债的票面价值决定了可转债的纯债价值（Pure Value）以及转股数量，而纯债价值是考虑违约风险时测算可回收价值的基础。

息票利率（Coupon Rate）决定了债券持有人享有的债券收益，进而影响可转债的纯债价值。发行人对支付可转债利息采用的息票利率可以是固定的也可以是浮动的，不同形式的息票利率在实际操作时的繁简程度会存在较大差异。

存续期限是指可转债从发行日至到期日的时间长度，是可转债的有效期限。可转债的存续期限一般由发行公司根据自己的偿债计划、偿债能力、股本扩张计划等情况制定。可转债存续期限越长，投资者面临的不确定性、违约风险越高，要求的风险补偿也就越高，因此会影响可转债的价值。

违约风险直接影响可转债内嵌权利的执行以及可转债作为纯债的价值回收情况。一般来说，违约风险越高，可转债的回收价值就会越低，可转债的价值也会越低。

（二）嵌入期权价值影响因素

可转债中的嵌入期权赋予债券持有人或发行人一定的权利，包括转股权、赎回权、回售权和转股价格向下修正权等，不同权利的价值影响因素也有所不同。

转股权的标的资产是公司股票，当可转债持有人在满足一定条件执行转股权时，股价的高低将直接影响可转债的价值，而转股时股价的高低受到股票波动率、转股期限及转股数量、转股价格等多种因素的影响。一般来说，股价波动率越高，意味着未来公司股票价格上升的空间就越大，可转债能够获得的转股收益也会越高，可转债的价值就越大；转股期限是指可转债持有者能将债券转换为普通股的起始日至截止日的时间，可转债的起止时间直接影响转股权利的行使时间，进而影响可转债的价值；转股价格越高，转股数量越少，转换价值就越低，可转债价值也就越低。

赎回权的行使一般会受到赎回期限、赎回价格及赎回条件等几个要素的影响。就赎回期限而言，赎回期限越短，可转债持有者通过股票増长行使转股权的机会就越大，可转债价值也会越高，反之则越低；赎回价格是发行人按照约定赎回可转债的价格，一种是按照可转债面值赎回，另一种是面值加当期（应计）利息赎回；赎回条件的设置是赎回条款的关键内容，直接决定了赎回权对可转债价值的影响程度，赎回条件越宽松，对可转债价值产生的负面影响越大，可转债的价值就越低。

回售权使可转债持有人有权按事先规定的价格将债券卖给发行人，当股价大跌或面临发行人信用危机时，债券持有人可行使回售权以最大限度地减少损失。相对于赎回权而言，回售权是保护投资者的一种权利，因此具有回售权的可转债价值更高。回售权的行使主要包括回售期限、回售价格及回售条件等要素，可转债回售期限越长，回售条件越宽松，可转债价值就越高，反之则越低。

转股价格向下修正权是指发行人具有对转股价格进行调整的权利，主要有两种情形：一种是标的股票出现分红、增发、送股等行为时，发行人可根据股票市场表现调整转股价格，以消除股利发放和股票数量变化导致的股票价格变化对可转债价值的影响，保护可转债持有者的利益；另一种是当标的股票价格长期下行出现预先设定的情形时，发行方可向下修正转股价格，以保证可转债价值的同时确保可转债持有者能够尽可能多地转股，降低大规模偿债的风险，但这种修正除了股价需要满足一定的条件外，最终是否要对转股价格进行修正还需要经过股东大会的投票同意。

三、二叉树期权模型在可转债定价中的应用

（一）定价原理和思路

1.只有转股权的可转债定价

以一个零息可转债为例，假设持有人在可转债存续期内能够将面值为N的可转债转换为Cr股、股价为S 的股票，那么该可转债的价值就是获得本金（即面值）与获得转股价值之间的较高者，用公式可表示为：

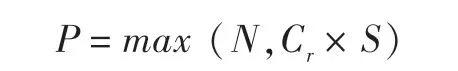
为进一步理解上述零息可转债的价值等式，可以对其进行分解，将max 函数中两部分分别减去面值N，得到：

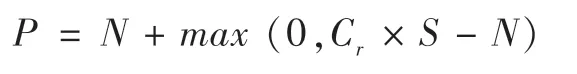
此时该可转债的价值等于普通零息债券的面值加上一个看涨期权的价值即这个看涨期权的价值也是转换权的价值，其中执行价是票面价值N，只要转股价值高于面值，可转债持有人就会行使转股权，可转债价值也会高于票面价值。

需要注意的是，若该可转债只有在债券到期时才能行使转股权，则上述看涨期权就是一个欧式看涨期权，在不考虑违约风险及利息支付的情况下可采用标准BS 模型对其进行定价：

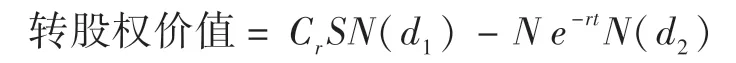
式中：

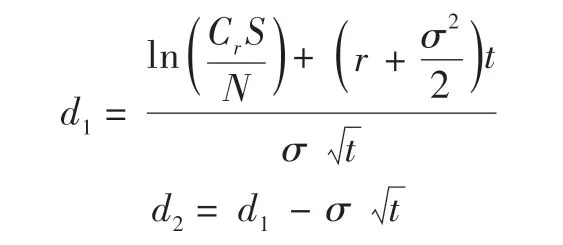
其中：S是持有人在转股时标的股票的市场价格，为转换率，N为可转债票面价值，t是可转债的存续期限，r是对应于该期限的无风险利率，是标的股票的波动方差。

然而，现实中可转债一般在发行一段时间后（常见是6 个月）至债券到期前都具有转股权，此时上述看涨期权就是一个美式看涨期权，再加上很多可转债在其存续期内的不同时点都有付息的要求，如需要较为准确地衡量可转债的价值，违约风险就需要被考虑进来，此时求解其价值就需要采用其他定价模型如二叉树模型，关于二叉树模型的具体应用将在后面以实例的形式做详细介绍。

2.加入赎回权和回售权的可转债定价

具有赎回权的可转债，发行人会根据债券的存续价值①对应时点可转债未行使任何权利的价值（Continuation Value）与赎回价值的大小判断是否进行赎回，然后可转债持有人会再根据股价及相关条件判断是否转股或者回售，这一过程决定了可转债的定价思路，可用函数表示如下：

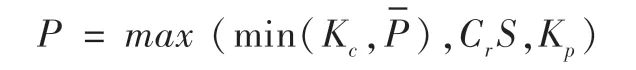
显然，对于具有赎回权和回售权的可转债，BS模型已经无法解决其定价问题，此时以股价为判断标准并行使各种权利的可转债定价问题，就可以利用二叉树模型在确定股价走势的基础上，对赎回权、回售权及转股价格向下修正权进行判断，进而确定二叉树各节点上可行使的权利，据此对各节点的可转债价值进行测算。具体来说，利用二叉树对上述可转债进行定价的主要思路是：

第一步：研究发行人标的股票的基本信息以及可转债的具体条款，比如股票价格、股息率及历史波动率、可转债各种内嵌权利的要求，包括但不限于各权利的触发条件、执行价格、行使时间及期限等与可转债价值有关的信息。

第二步：确定股价二叉树模型的上升因子u、下降因子d以及上升概率pu和下降概率pd，在考虑违约风险时还需要确定发行人的违约概率pb。常用于可转债定价的二叉树模型是基于Cox,Ross and Rubinstein（简称CRR）提出的股价二叉树模型（简称为CRR tree），在该模型中不考虑违约风险和考虑违约风险的各因子测算公式如下：

（1）不考虑违约风险的股价二叉树：

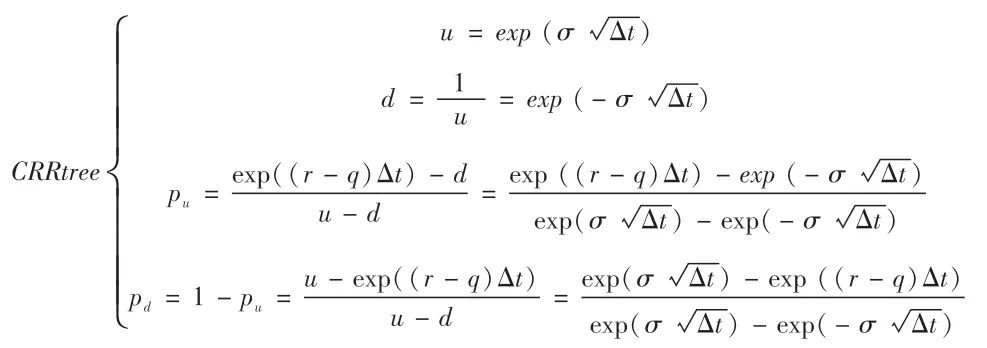
（2）考虑违约风险的股价二叉树：

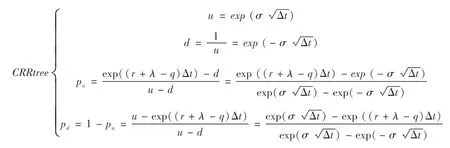
两个模型的相同参数具有相同的含义，主要差异在于参数λ，λ被称之为违约密度（Default Intensity），是时间的函数，在应用中常被设定为一个常数，也可用违约概率（Default Probability）倒推获得。已知违约密度，则发行人的违约概率可表示为：

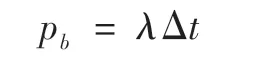
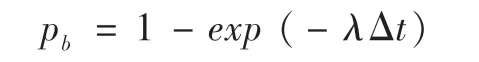
第三步：根据股价二叉树模型模拟股价走势路径，并计算各节点的股价。股价二叉树可以用图2表示，实线代表各节点股价均经历上升和下降两个走势，虚线部分表示发行人公司破产，此时股价降为0。

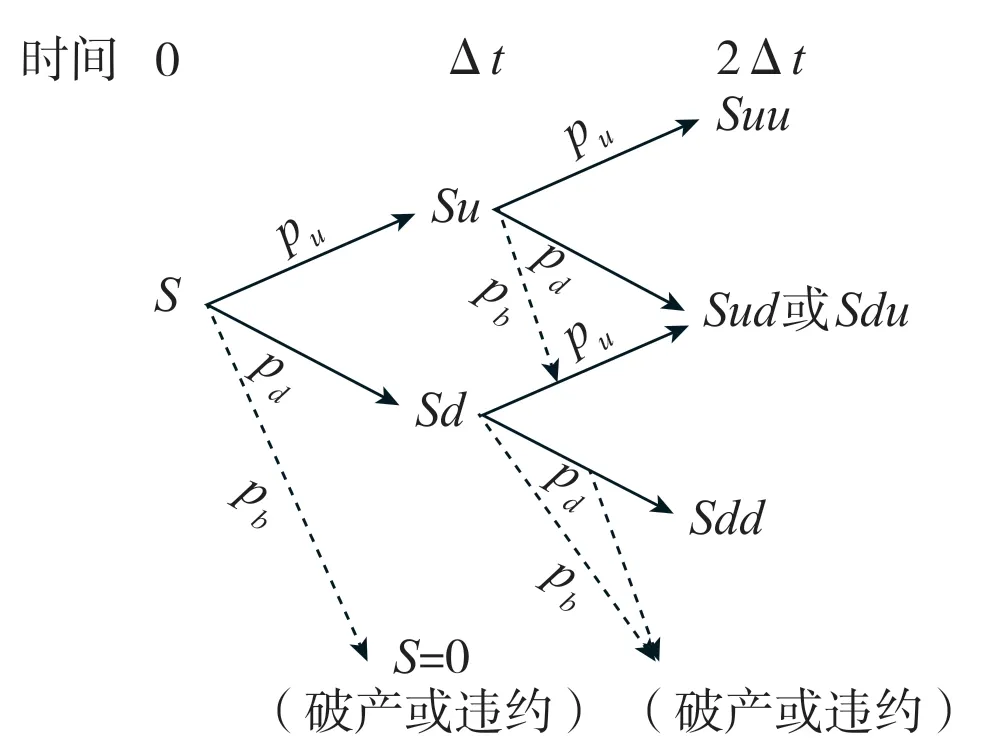
图2 股价二叉树走势

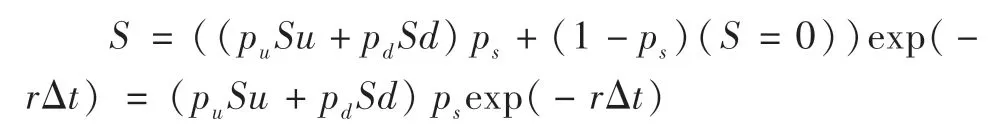
等式两边同时除以S，则有：

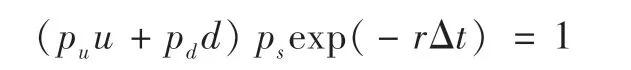
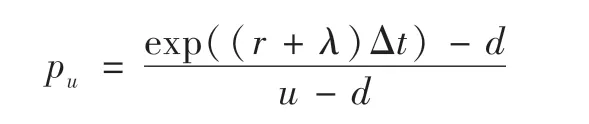
若考虑股息率q的影响，则上式就变成：

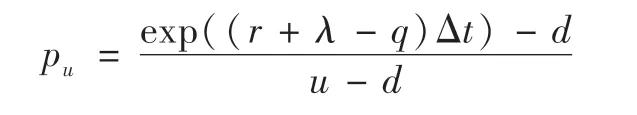
这一推导过程能够很好地理解股票上升与下降概率的含义，尽管式中含有违约密度，但其中并不包含违约概率，这一点从股票价格S 等式中可以看出来。理解这一点非常重要，因为在计算可转债价值时，和也会同时出现在其定价公式中，切忌出现因中含有违约密度就不再考虑违约风险或违约概率而造成的错误。

第四步：利用股价二叉树测算各节点的转股价值并结合可转债各项权利条款判断是否触发赎回权、回售权，对于设置转股价格向下修正条款的可转债，需要根据各节点股价进行判断并确定新的转股价。

转股价值直接决定可转债价值的大小，但赎回权、回售权则影响转股的执行时间和执行效果。利用股价二叉树判断各节点是否触发赎回、回售等条款，为发行人和可转债持有人确定最佳的执行策略提供依据，作为确定各节点可转债价值的基础。

第五步：确定各节点的可转债价值，形成可转债价值二叉树。各节点的可转债价值可根据下列公式测算：

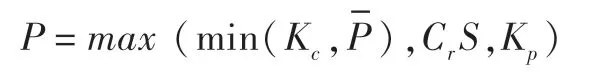
在可转债价值二叉树的终端节点，可转债的存续价值等于其面值加上当期（应计）利息，即到期时可转债持有人收到本金和利息，在二叉树的中间节点，存续价值等于后一节点的可转债价值经过折现并乘以相应的概率进行求和，同时考虑当期利息的影响，用图形表示如图3：

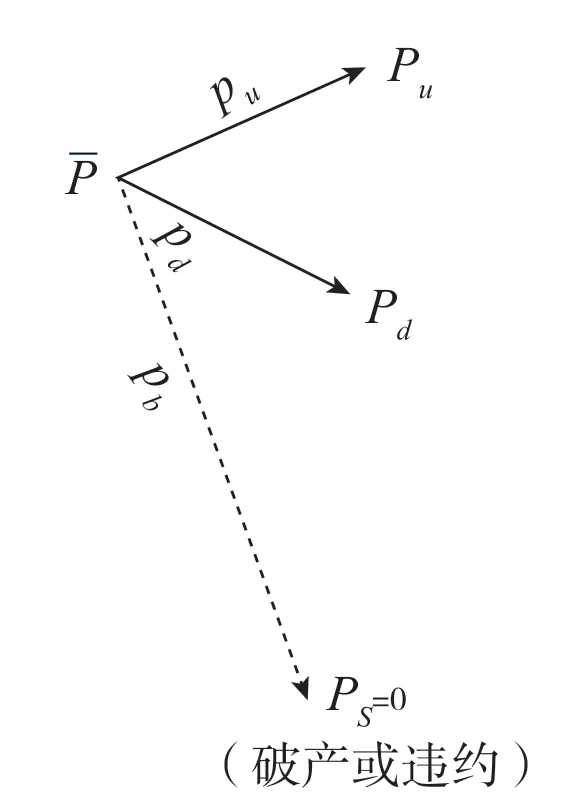
图3 可转债的存续价值

用公式表示可转债的存续价值，则有：

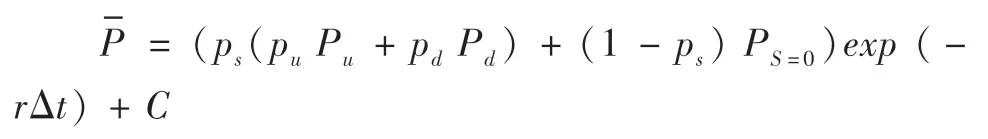
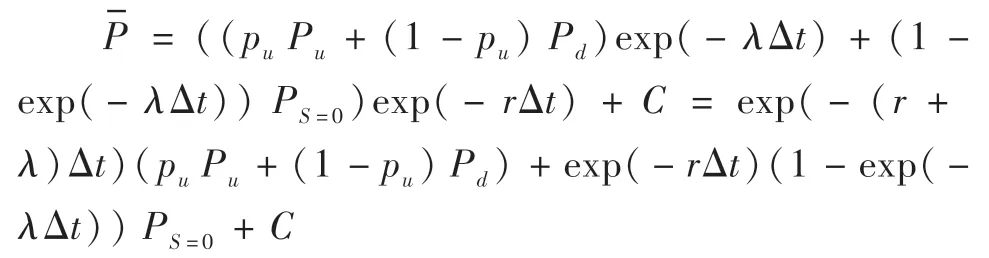
需要说明的是，发行公司在发生破产或违约时，公司股价降为0，可转债作为固定收益证券的价值也将面临损失，即还本付息部分也会出现支付困难，但债券持有人享有标的公司变卖财产并给予优先支付的权利。根据优先级及有无担保的不同，债券面临违约时的回售率（Recovery Rate）有很大差异。下表是穆迪评级公司公布的不同级别的公司债在违约时的回售情况，优先级越高，平均回收率越高；有抵押担保债券回收率高于无抵押担保债券的回收率，优先支付且有抵押担保的债券平均回收率在50%左右，次级债券回收率在30%左右甚至更低。

因此，在发行公司面临破产或违约时，可转债在到期时的可回收价值可表示为：

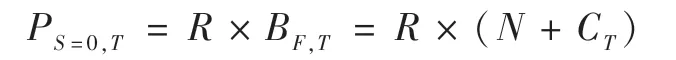
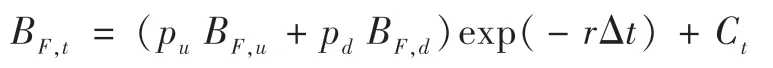
Ps=0,t=R×BF,t

第六步：确定评估时点可转债的理论价值。发行人与可转债持有人在各节点做出了理性决策之后，根据各节点已知的赎回价格、可转债存续价值、转股价值及回售价格，各节点的可转债价值就可以根据进行确定，并成为前一节点求取可转债存续价值的基础，如此循环往复直到第一个时点，经过折现就能得到评估时点（t=0 时刻）的可转债理论价值，公式如下：

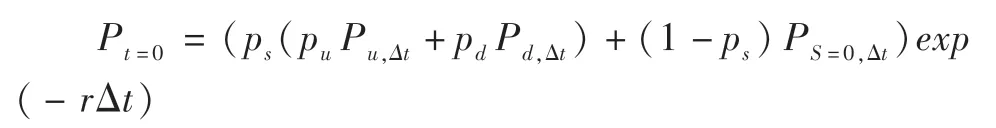
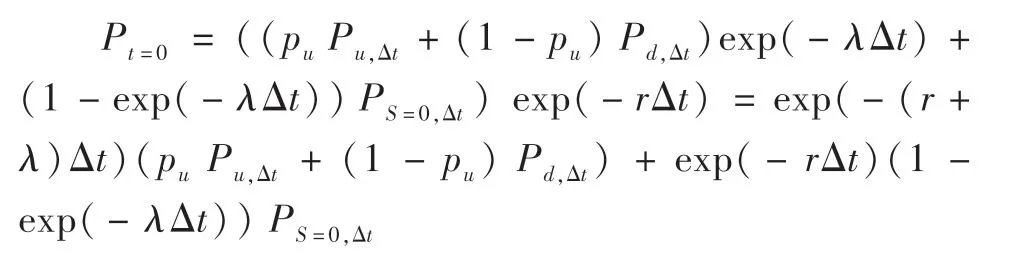
（二）应用举例

本案例以国内A 上市公司发行的A 可转债为例，展示二叉树模型在可转债定价中的具体应用，为评估人员实际操作提供更为直观的理解。

为重点说明二叉树在可转债定价中的应用思路，本案例将该可转债的具体信息做了一定的简化处理，比如付息日定在每年年底，赎回权、回售权和转股价格向下修正权的触发条件由多个交易日股价满足某一水平的要求简化为对各节点股价是否满足该要求的判断。根据A 公司发布的《公开发行可转换公司债券上市公告书》中的信息，该可转债重要的条款信息简化如下表2所示。

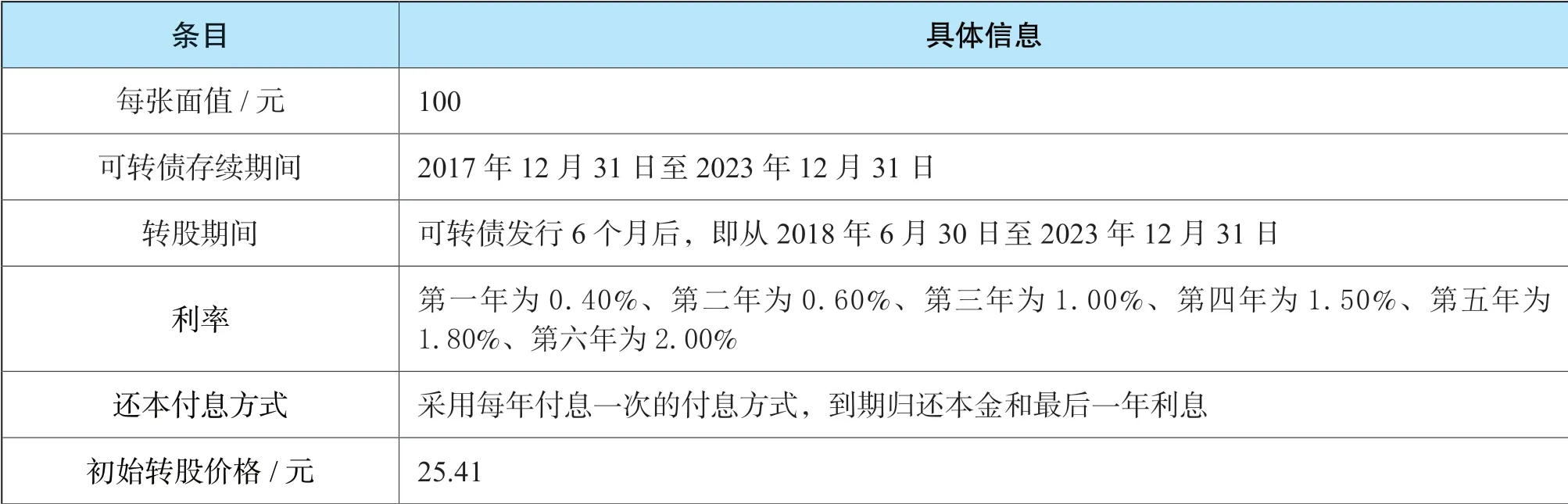
表2 A 可转债条款信息

续表

根据上述可转债具体条款的内容，可提炼出二叉树定价模型所需要的参数信息如表3所示，其中股票波动率及违约密度是主观给定的，实际操作中可结合发行公司标的股票的历史数据表现采用一定的方法对其进行量化，或对管理层进行访谈得到，在此暂不做赘述。

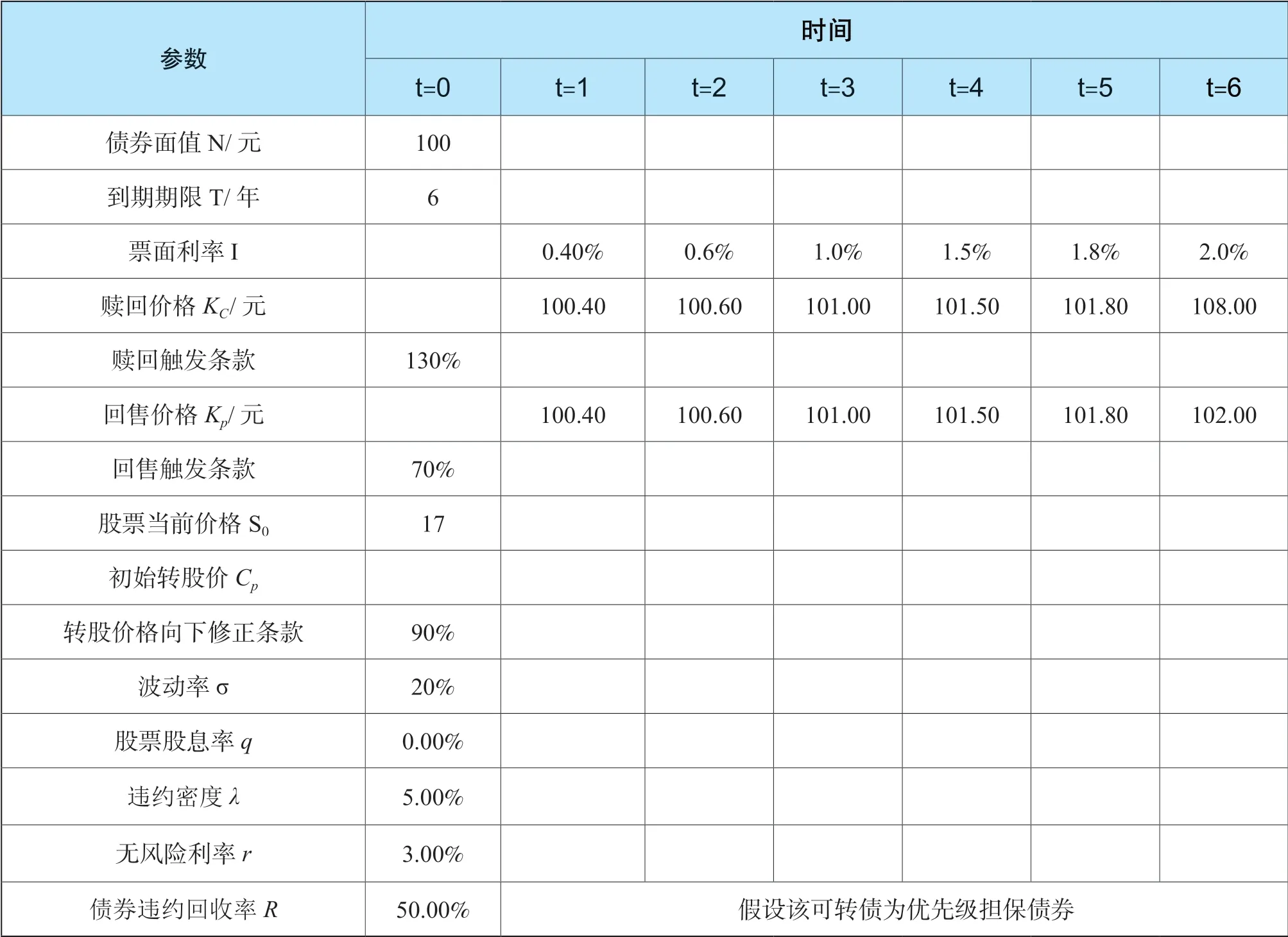
表3 二叉树模型对可转债定价所需的基本参数信息

根据CRR 模型可以测算二叉树模型所需的上升因子、下降因子，上升概率和下降概率等参数，如表4所示。

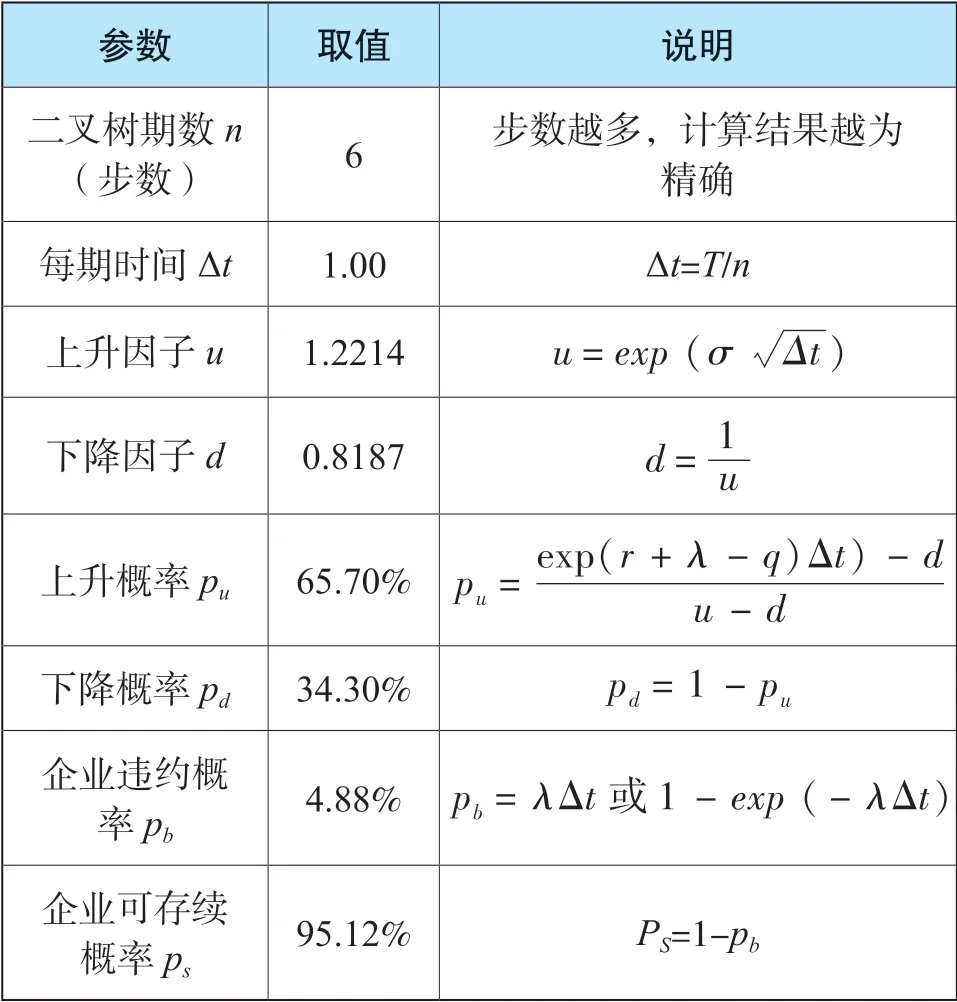
表4 参数测算结果

根据上表具体参数信息，股价二叉树可表示如表5所示。

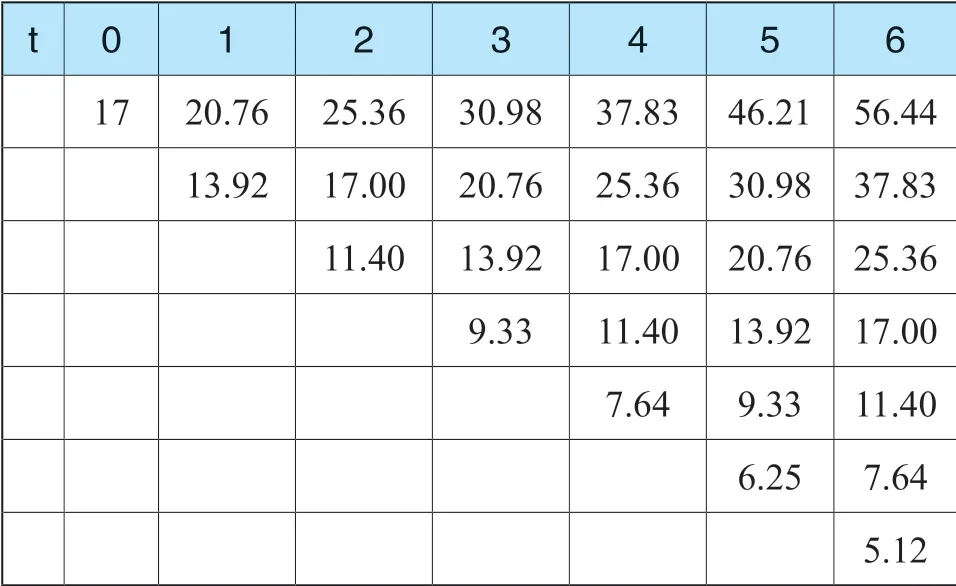
表5 股价二叉树测算结果

得到股价二叉树之后，需要根据各节点的股价水平判断是否触发转股价格向下修正条款，以此确定各节点最新的转股价格。

对于股价始终处于上涨和始终处于下跌的两条特殊路径上的节点，由于到达这些节点的情形只有一种路径，因此可以直接通过转股价格向下修正条款的约束进行确定，即当前股价水平是否低于当期转股价格的90%，如果是，则将当前股价水平作为最新的转股价；如果不是，则保持当期转股价格不变。

对于其余股价节点，都由前一期两个股价路径经过下降、上升而来，回溯每种到达该节点的股价路径，通过可转债的特别向下修正条款确定该路径上哪些节点的转股价格需要进行修正。对于每一条可能的股价路径，都可以得到一个转股价格，而该二叉树节点对应的转股价格即是所有股价路径对应的转股价格的期望，即：

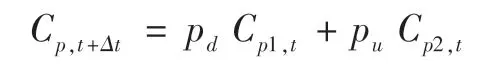
通过对各节点股价水平的判断，形成的最新转股价二叉树如下表6所示，表中蓝色部分的每一节点转股价均是其对应股价路径上各转股价格的期望值。

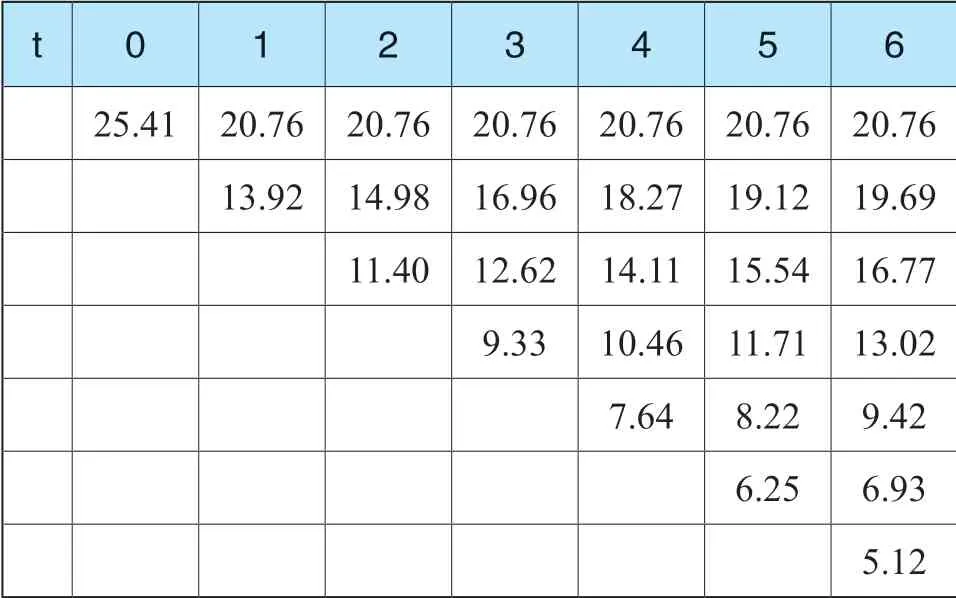
表6 最新转股价二叉树

同样地，根据各节点股价水平以及赎回、回售条款的要求，对各节点是否触发赎回或回售进行判断，即该节点股价是否高于当前转股价的130%（触发赎回）还是低于当前转股价的70%（触发回售），判断结果如下表所示，“-”表示既没有触发赎回，也没有触发回售。需要注意的是，根据条款信息，发行人在可转债发行6 个月后至可转债到期（即t=1 至t=6）在满足条件的情况下均具有赎回权，而可转债持有人仅仅在到期前两年（即t=5 和t=6）满足条件时才具有回售权。

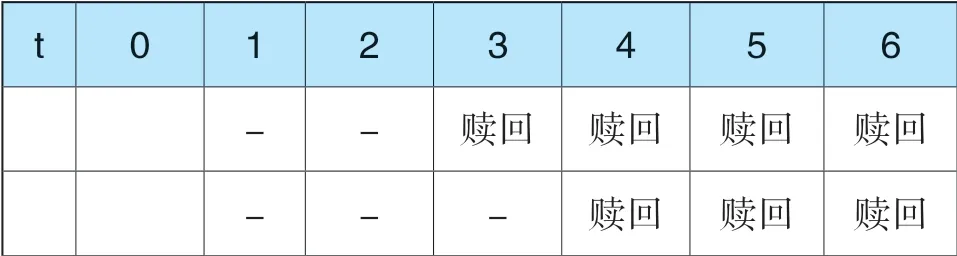
表7 不同时点触发的权利

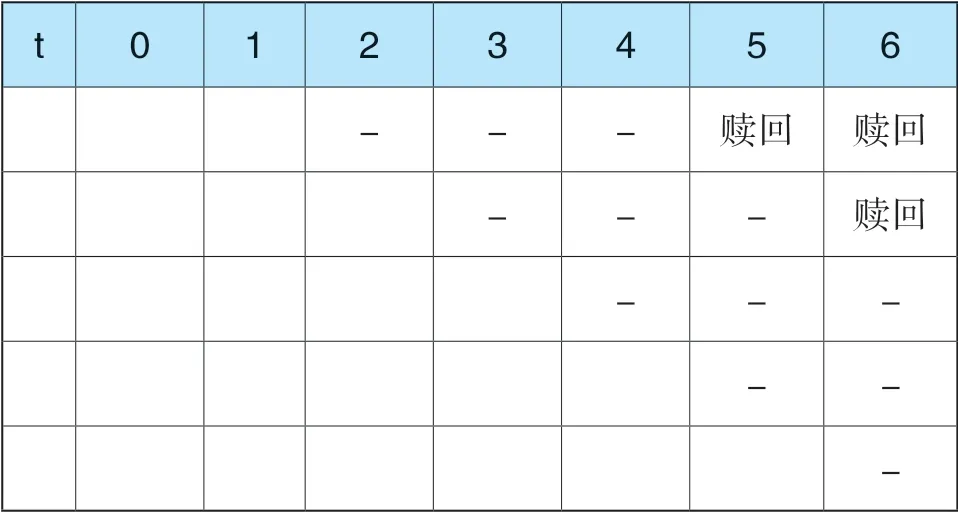
续表

明确了各节点最新转股价以及触发的权利条款，可以得到各节点的转股价值、纯债价值（用来确定各节点违约时的债券可回收价值）、存续价值以及可转债理论价值，由于存续价值的计算会用到它后一节点的可转债理论价值，因此在此仅展示可转债的转股价值、纯债价值及理论价值，测算结果分别如表8、表9、表10所示：

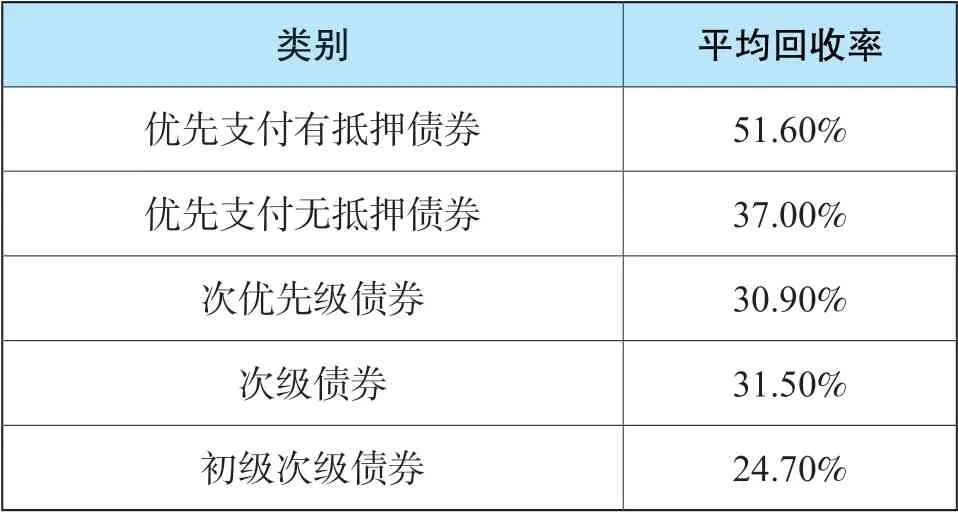
表1 1982～2012年企业债券的回售率（面值百分比）

表8 转股价值二叉树（转股价值

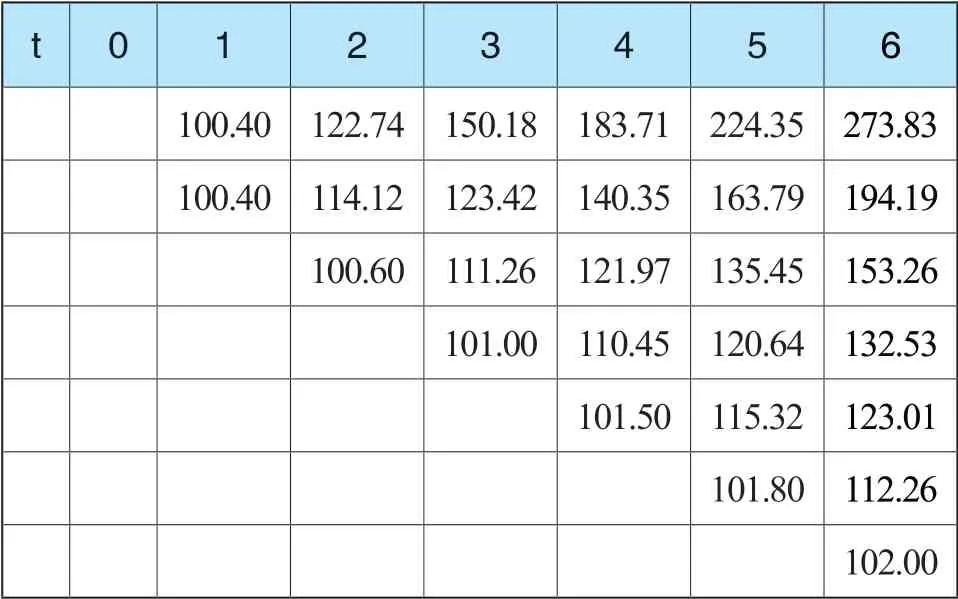
表8 转股价值二叉树（转股价值

t 0 1 2 3 4 5 6 100.40 122.74 150.18 183.71 224.35 273.83 100.40 114.12 123.42 140.35 163.79 194.19 100.60 111.26 121.97 135.45 153.26 101.00 110.45 120.64 132.53 101.50 115.32 123.01 101.80 112.26 102.00

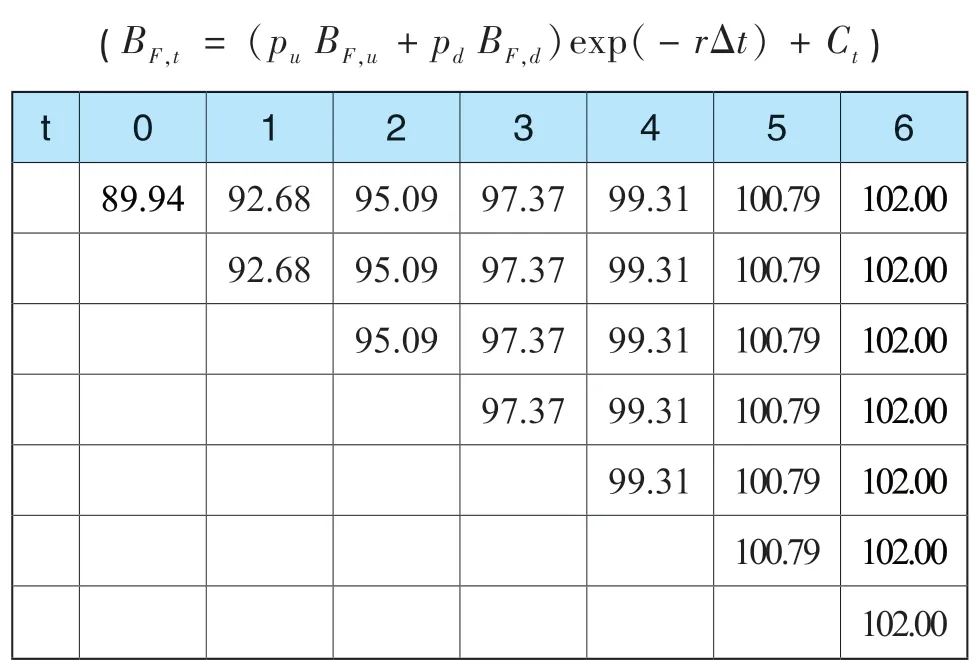
表9 可转债的纯债价值

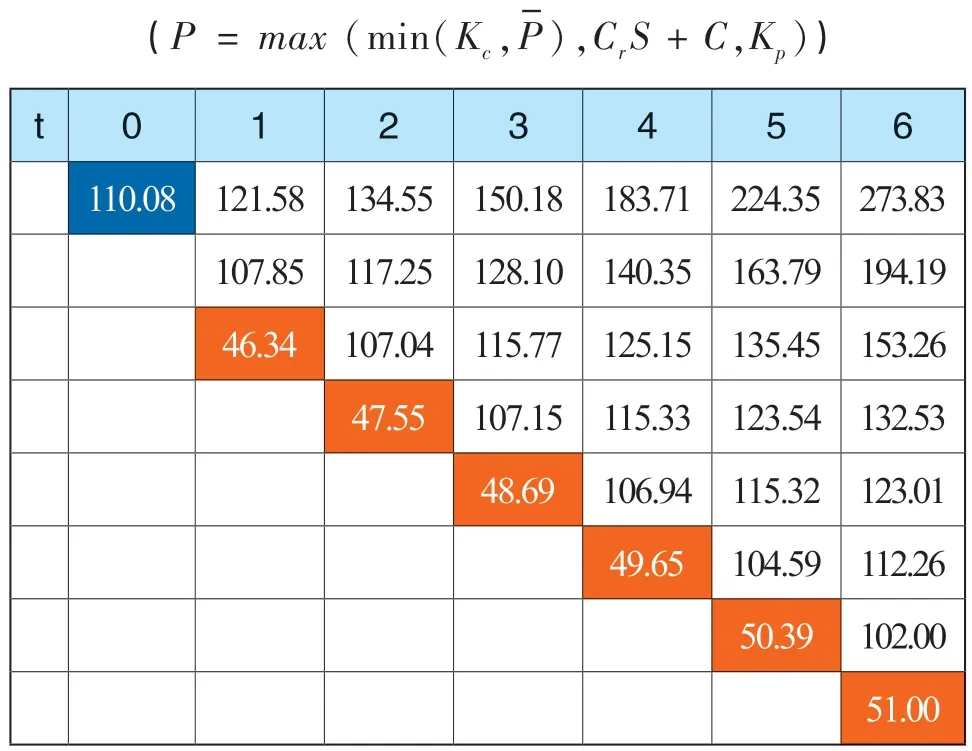
表10 可转债的理论价值

需要说明的是，表10 橙色单元格表示可转债面临违约时的可回收价值（各节点可回收价值回收率×该节点对应的纯债价值），以体现违约风险对可转债价值的影响，考虑了违约风险后的可转债价值树更像是三叉树模型，这也是很多研究学者在引入波动率、利率和违约密度函数等更复杂情形时直接建立三叉树模型的原因。

通过以上计算过程，该可转债的理论价值为110.08 元。

四、小结

可转债除了具有转股权以外，还有很多其他附加权利，如赎回权、回售权和转股价格向下修正权，加上这些权利的行使期限一般会贯穿可转债整个存续期间，因此用来对欧式期权进行定价的标准BS 模型对可转债评估就具有较大的局限性。而二叉树定价模型的理论相对成熟，且能够兼顾利率、股价以及可转债违约风险等影响可转债价值的诸多因素，是对可转债较为合适的定价方法。虽然也有很多学者采用蒙特卡洛模拟最小二乘法对可转债进行定价，但该方法需要模拟大量的路径，同时还需要对每条路径的中间时点都需要进行策略判断，然后进行价值回归，定价精度的提高伴随着较大的时间成本；此外，蒙特卡洛模型较少也难以衡量违约风险对可转债价值的影响。综上，二叉树定价模型是理论与实务中解决可转债定价问题较为适用的评估方法。