随机森林房地产自动评估模型构建及其比较研究

■公云龙 杨雨涵，2

（1.中国矿业大学公共管理学院，江苏徐州221116 2.香港理工大学土地测量及地理资讯学系，香港810005）

一、引言

大数据时代，随着不动产特征及其交易数据可获性的大幅提升，使自动评估模型成为税收、信贷等批量评估领域关注的热点。2003年，国际估税官协会（International Association of Assessing Officers,IAAO）发布了《自动评估模型准则》（《Standard on Automated Valuation Models》），对自动评估模型的构建过程、建模技巧、应用范围等进行了规范。相对而言，我国对批量评估和自动评估模型的研究起步较晚，早期主要集中于将GIS 与估价方法相结合以构建评估系统[1-2]。

房地产自动评估模型依赖于计算机和数学模型，其核心是挖掘房地产价格与其影响因素之间的定量关系并将其用于待估房地产价格的预测。特征价格模型是构建自动评估模型时最常用的数学模型之一[3-4]。特征价格模型能够量化单因素对房地产价格的线性影响，而房地产价格通常受相互渗透、复杂多变的各个因素的交互综合影响，为此，国内外学者开始将机器学习算法应用于房地产自动评估模型的构建，以刻画房地产特征对价格的非线性和交互影响。当前，已有众多研究构建了基于神经网络的自动评估模型，针对神经网络评估模型的稳定性、评估精度、收敛速度、泛化能力等问题进行了深入探讨[5-8]。除此之外，也有学者探讨了基于支持向量回归的自动评估模型的构建问题[9]。

相比于神经网络模型和支持向量回归模型，回归树算法原理简单、计算速度快且可以处理连续和分类变量，也因此被广泛应用于自动评估模型的构建。当前，已有研究表明基于回归树的集成算法—随机森林模型，在自动评估模型的评估精度方面具有一定的优越性[10-13]。为进一步揭示随机森林自动评估模型的构建特点及优势，本文将深入研究随机森林模型的参数设定对评估效果的影响，并从评估精度、模型泛化、经济解释等方面将其与常用的Hedonic 模型、BP 神经网络和支持向量回归自动评估模型进行比较分析，总结随机森林自动评估模型的应用特点并指导实践。

二、随机森林房地产自动评估模型构建原理及精度评价方法

给定一个容量为n的房地产交易数据集，并将其随机分为容量为nt的训练集和容量为nr的测试集（n=nt+nr），同时将影响房地产价格的特征因素标记为xj(j=1,2,…,m)。本文将运用训练集训练随机森林自动评估模型，并利用测试集进行精度分析。

（一）回归树模型

回归树是一种应用于因变量为连续变量的决策树[14]，是随机森林自动评估模型的机器学习。回归树模型利用树形结构将房地产交易数据集划分为若干子集（C1,C2,…,CR），并利用子集内样本价格进行价格评估，即一棵典型的回归树由根节点、内部节点和叶节点组成。根节点是包含数据集中所有数据的节点；根节点包含判断条件，以此为起点生长回归树，分裂过程将形成多层内部节点，每个内部节点代表数据集中满足从根节点到该节点所有判断条件的数据集合；最终形成的具有相似特征的数据子集称为叶节点，也即用于进行房地产价格预测的数据集。

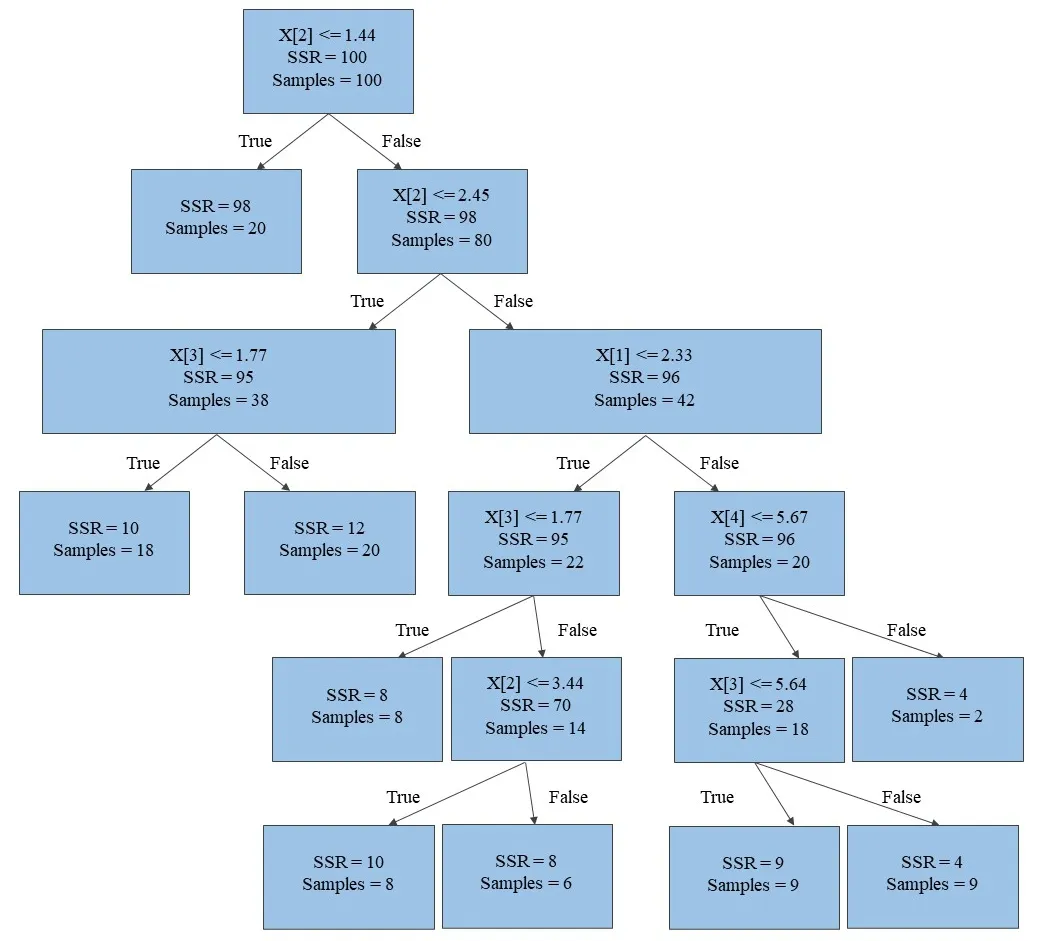
图1 回归树原理图

在每个根节点或内部节点分裂生长回归树自动评估模型时，需以最小化两个分支样本的预测残差平方和为目标，采用启发式方法确定最佳切分特征变量（Xj）和切分点。构建回归树自动评估模型时还需确定树的高度或深度，预剪枝和后剪枝是两种常用的方法。前者在构造回归树时进行剪枝，比如提前确定树的深度，但此种方法的效果较差；后剪枝则先构造一个大的回归树，再根据叶节点合并前后预测误差的变化来确定是否删除子树[15]。目前最常用的回归树生长算法为CART（Classification and Regression Tree）算法。

（二）随机森林自动评估模型

当回归树自动评估模型的节点分裂深度较大时，容易出现过拟合[16]。随机森林回归（Random Forest Regression）是一种由Bagging 算法改进的基于回归树的组合算法，可以有效解决回归树模型的过拟合问题。随机森林自动评估模型的构建过程为：

（1）运用bootstrap 法从训练集中随机有放回的抽取容量为nt的k个训练样本，每个训练样本通常只包含原始训练集2/3 的样本，另外1/3 未被抽取数据被称为袋外数据（out of bag——OOB）；

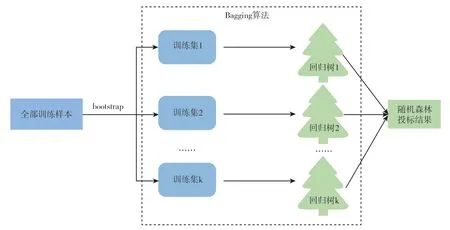
图2 随机森林原理图

（2）对于每个训练样本，在每个分裂节点处从m个住房特征中随机抽取h个特征并运用CART 算法分裂构建回归树（m≤h）；

（3）将生成的k棵回归树组成随机森林，由k棵树预测值的均值决定最终预测结果。

基于袋外数据OOB，随机森林模型可以对特征变量的重要性进行评价。将每个训练样本的回归树模型应用于袋外数据时，将得到袋外数据的均方根误差（MSEOOB1）；进而对OOB 样本的特征xj随机加入噪声干扰，也即随机改变特征变量xj的值，再次得到袋外数据均方根误差（MSEOOB2），最后计算该值越大，说明该变量xj在回归模型构建中越为重要[16]。

（三）精度评价方法

运用训练集构建随机森林自动评估模型后，可以运用测试样本对模型的评估性能进行验证与评价，评价过程以模型对测试样本预测值与测试样本实际值的各项误差为基础。本文借鉴其他学者[17]的研究，选用R2、均方根误差（RMSE）、平均绝对误差（MAE）和平均绝对百分比误差（MAPE）作为模型预测精度的评价指标。其中RMSE、MAE、MAPE的计算公式分别为：

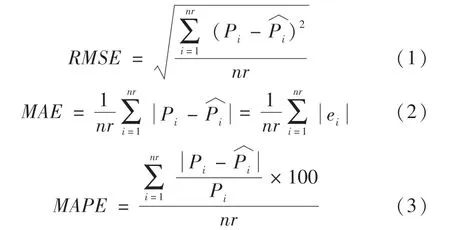
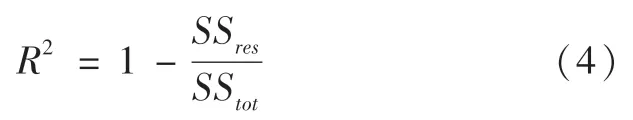
三、数据与变量

（一）研究区及数据

本文以江苏省徐州市泉山区和鼓楼区的二手房交易市场为研究对象。从图3 可以看出，2018年1月—2020年8月徐州市鼓楼区房价稍低于泉山区房价，体现了两个区的区位差异。但从长期发展趋势看，泉山区与鼓楼区的住房均价变化趋势基本一致，可以将泉山区与鼓楼区房地产市场看作为同一房地产市场。

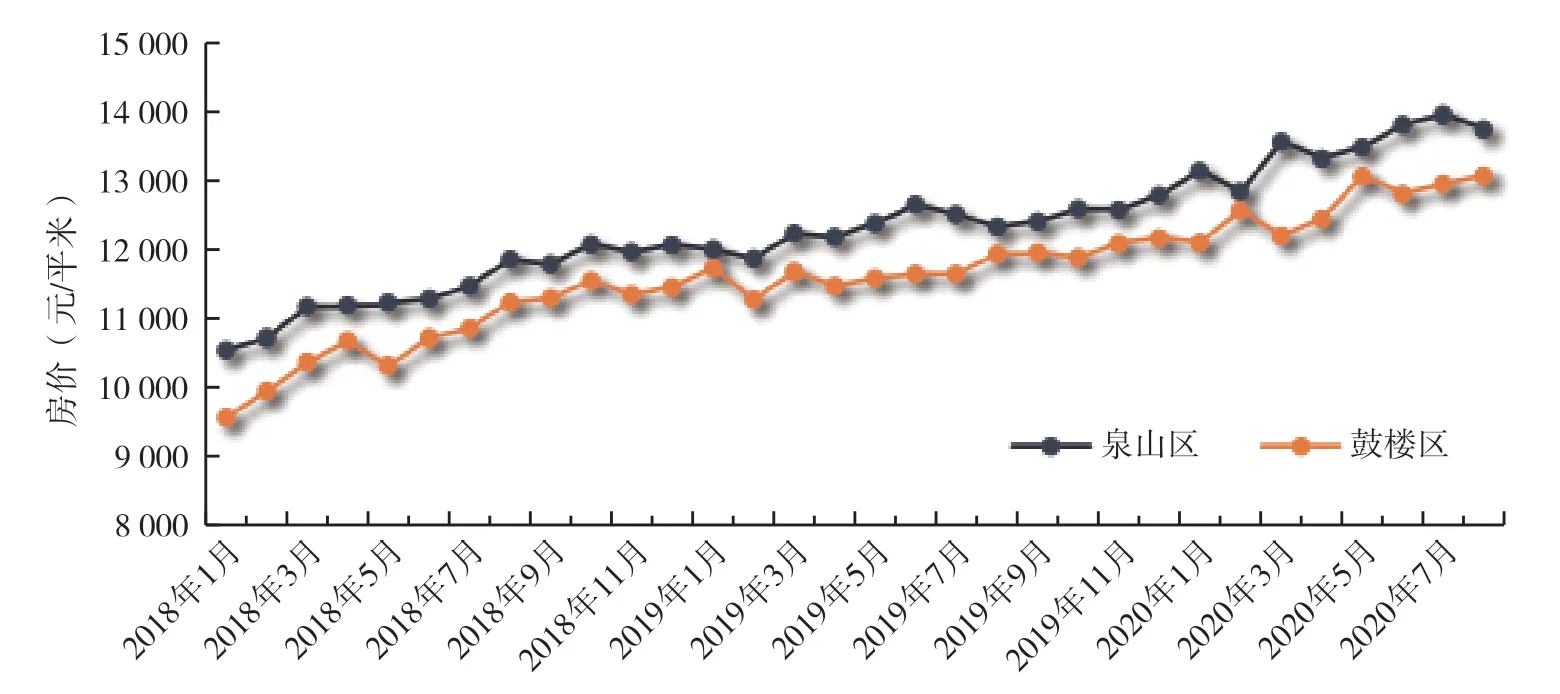
图3 徐州市泉山区与鼓楼区2018年1月—2022年8月房价走势图

本文从禧泰房地产大数据（cityre.cn/credata.html）收集了泉山区和鼓楼区2018年1月—12月的二手房首次挂牌案例，共85 037 条记录，涵盖787个小区①。删除异常值、无效值和缺失值的挂牌案例后，本文将剩余的21 590 条记录作为样本集，涵盖361 个小区。该样本包括房产的地理位置、建筑面积、房龄、所在楼层和总楼层、房型、装修程度等14 个特征的相关信息。与此同时，本文根据房产的位置信息，利用GIS 计算了各案例到城市中心的距离。教育配套、基础与公共设施配套等信息则来源于房天下、安居客等在线房地产中介网站的评价信息。

（二）变量设定

一般而言，房地产价格的影响因素包括一般因素、区位因素和个别因素。由于本文搜集的二手房交易数据位于徐州市区内，具有相似的社会、经济和行政状况，一般因素在研究区内具有同质性，所以本文只考虑区位因素和个别因素的选取。借鉴其他学者的研究[9,18-19]，本文设定了6 个区位因素和8个个别因素作为房地产的特征变量。其中，区位因素DFC（距离市中心的远近）以苏宁广场作为商业中心，用ArcGIS 计算小区到商业中心的距离；因素SR（教育配套设施状况）的量化结合房天下（https://xz.fang.com/）网站公开信息，根据“是否为学区房”的评价标准，以0 或1 量化；因素FT（交通设施状况）为小区500m 半径范围内公交站点、地铁站点的数量；因素FPF（生活服务设施状况）为小区500m半径范围内医疗点、公园、银行、商场的总数量；因素PF（物业状况）和因素AR（绿化率）分别以小区物业费和绿化率的实际值量化。

在个别因素变量设定中，age（住宅楼龄）以2018年为基期，减去小区建成年代而得来；PR（容积率）为住宅所在小区的实际容积率；area（面积）为挂牌房地产的建筑面积。建筑结构、户型、朝向、装饰装修和层高则被转变为相应的0-1 虚拟变量，比如建筑结构被分解为砖木结构（BWS）、砖混结构（BCS）、钢筋混凝土结构（RCS）三个虚拟变量来表达。最终共获取26 个个别因素特征变量，各变量的定义及描述性统计信息见表1。

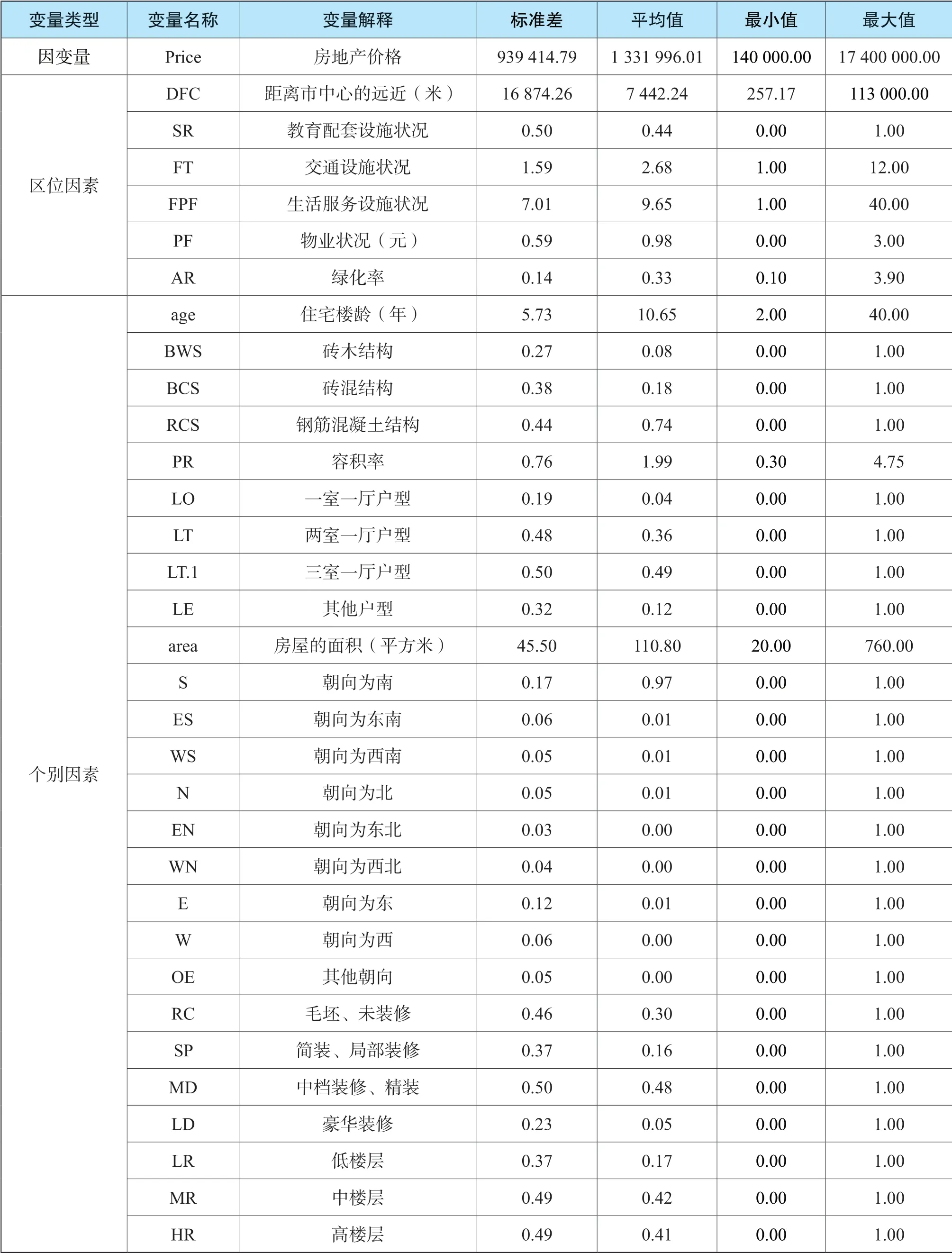
表1 因素的统计描述

① 房地产自动评估模型一般基于交易价格构建，但在我国当前的市场条件及环境下，真实的交易价格较难获取，因此本文用首次挂牌价格加以替代，并不影响自动评估模型的构建。根据数据提供方的统计，首次挂牌价格与真实交易价格的差距一般在15%之内。

四、随机森林自动评估模型训练及比较分析

（一）随机森林自动评估模型训练

本文随机将研究数据集划分为训练集与测试集，其中训练集包含17 285 条记录（占比80%），测试集共包含4 305 条记录（占比20%）。随机森林自动评估模型基于R 语言的randomForest 包构建，在构建过程中需要确定两个重要的超参数：（1）随机森林中回归树的棵数ntree；（2）回归树分裂时特征子集的特征个数mtry。本文将mtry 的范围确定为[5,32]，ntree 的取值范围确定为{500,1 000,1 500,2 000,2 500}，继而运用遍历法构建了140 个随机森林模型，并计算其拟合优度，其对应关系如图4所示。

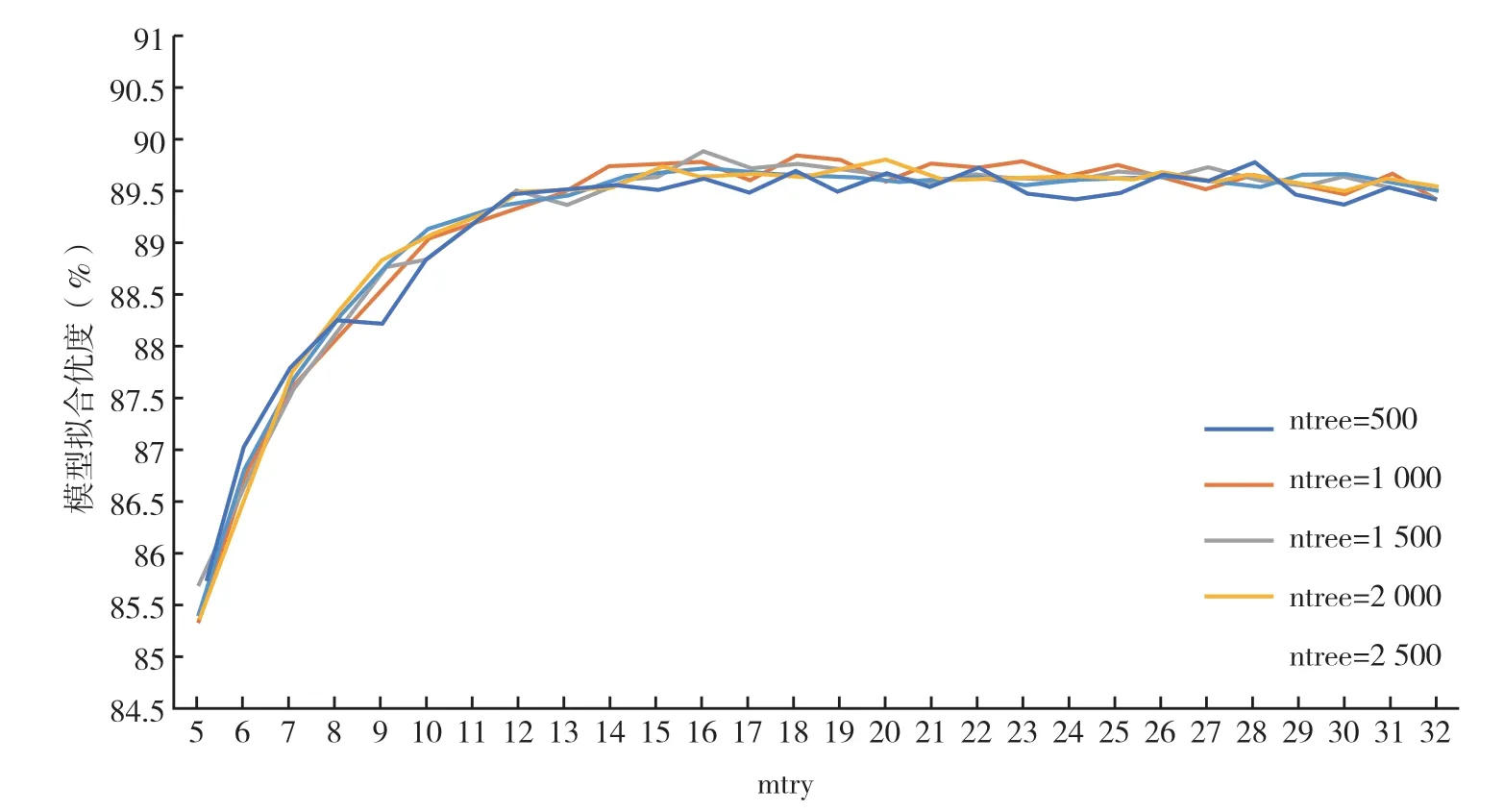
图4 随机森林超参数设定对拟合优度的影响

由图4 可以看出，随着特征个数mtry 的增加，随机森林自动评估模型的评估精度越来越高。但其变化呈现出非线性特征，当特征个数从5 增加到12时，随机森林模型的评估准确性上升较快，之后提升趋势变缓并趋于稳定，甚至略有下降。与此同时，通过比较包含不同回归树颗数的随机森林模型，发现ntree 的取值对模型拟合优度的影响并不显著。综合而言，当mtry ∈[15,18]时，包含不同回归树颗数5 个随机森林自动模型的拟合程度均可达到峰值。通过比较，发现当mtry=16、ntree=1 500 时，模型的拟合优度最高，因此将其确定为最优超参数。

最终构建的随机森林自动评估模型中回归树的统计特征如图5所示。在1 500 棵回归树中，最小的回归树包含5 350 个节点，最大的回归树包含5 600个节点，绝大部分回归树的节点数在5 450-5 500 之间。可以发现，随机森林自动评估模型中回归树的结构特征基本稳定，回归树节点深度在15 层以上，足以说明各变量对房地产价格影响的复杂性和综合性。

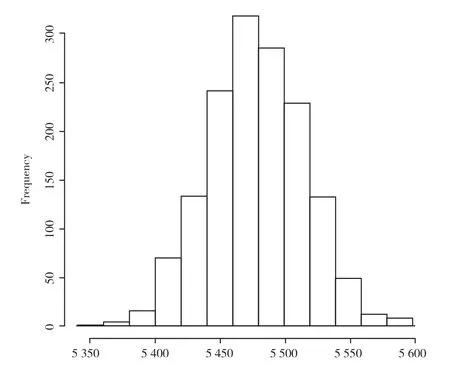
图5 随机森林模型回归树节点统计

根据表2，本文所构建的随机森林自动评估模型在训练集的拟合优度（R2）为90%，即能够解释90%的房价差异；平均绝对误差为151 714.10 元/套，平均绝对百分比误差为11.11%，即对于一套价值为100 万元的住宅，随机森林自动评估模型的估价区间为88.89 万元至111.11 万元之间，模型的预测精度较高。

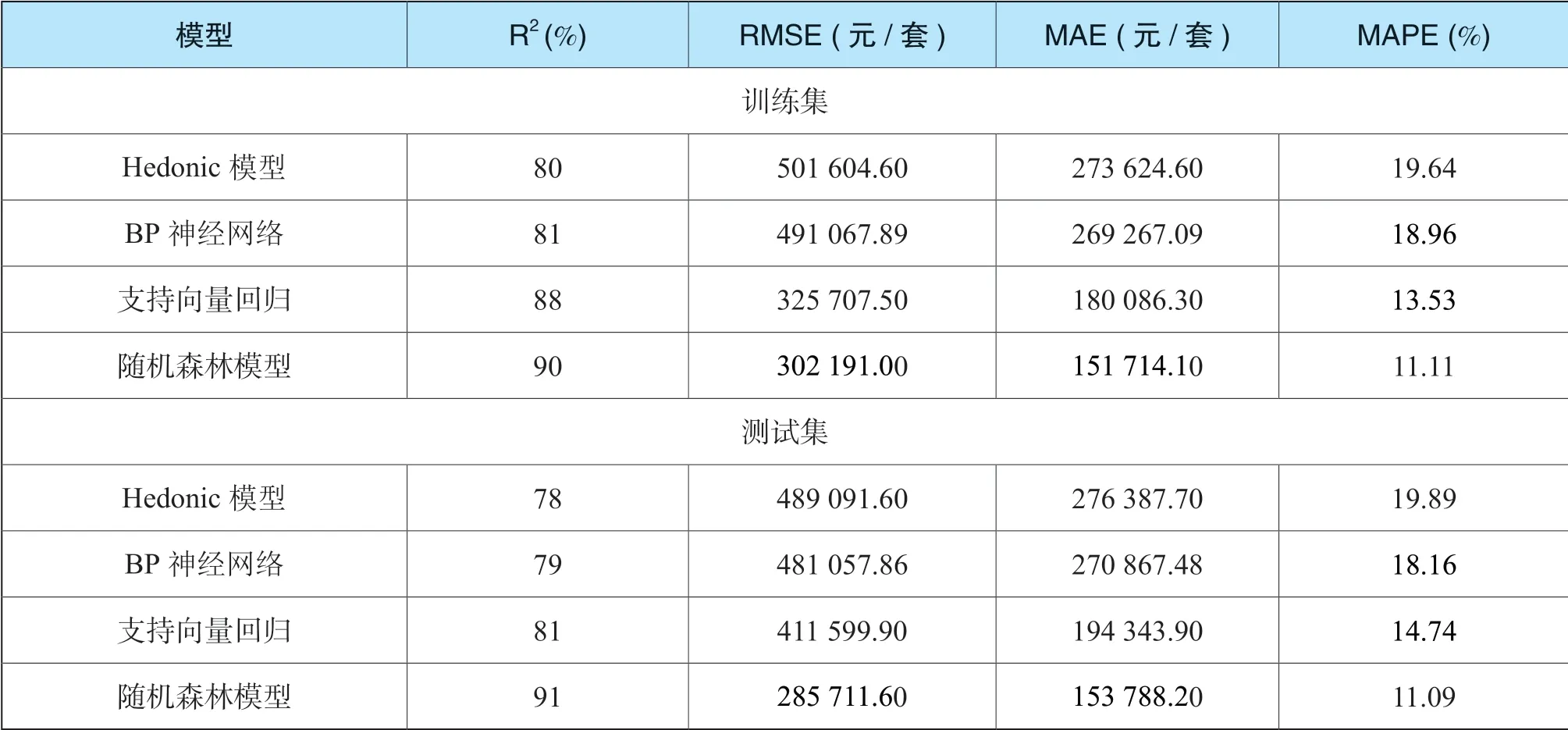
表2 模型预测效果对比

（二）评估精度及泛化能力比较

为进一步考察随机森林自动评估模型的评估精度及泛化性能，本文将此模型运用于测试集进行验证。结果表明，此模型在测试集中的表现稍好于在训练集中的表现，除平均绝对误差这一指标劣于训练集外，R2、均方根误差、平均绝对误差百分比三项指标均略好于训练集中的表现，表明本文所构建的随机森林自动评估模型具有较高的精度和较好的泛化能力，能够广泛的用于研究区域房地产的自动评估。

此外，本文还训练了Hedonic 模型、BP 神经网络和支持向量回归模型以进行不同自动评估模型的比较研究。上述4 个模型均用同一训练集进行模型训练，并用同一测试集进行模型预测效果检验。BP神经网络自动评估模型基于python 算法构建，核函数确定为ReLU，利用5 折交叉验证，构建了单隐层、双隐层、三隐层和四隐层网络，并对每层的神经元个数进行网格法搜索，最终确定BP 神经网络模型的隐含层数目为4，每层的神经单元数依次为30、30、10、10。支持向量回归自动评估模型的核函数设置为高斯径向基核，利用网格法寻找出最优的惩罚因子C 为108，径向基核函数参数为10-5。Hedonic模型则依据R2与残差分布，在线性、线性对数、对数线性和对数4 种函数形式中确定，最后优选出对数函数形式的Hedonic 模型。

所训练的4 个房地产价格自动评估模型的评估精度如表2所示。总体而言，四个精度测度指标均显示Hedonic 自动评估模型的预测精度低于其余三个机器学习自动评估模型的预测精度。其原因在于Hedonic 模型只能刻画房地产价格与特征之间的线性关系（或可转换为线性关系），而忽略了房地产特征对价格的非线性影响和交互影响[20]。机器学习模型是建立在房地产特征相互依赖基础之上的，能够对特征间和特征与价格间的复杂关系进行深度学习，从而使模型预测更为准确。

在基于机器学习的3 个房地产价格自动评估模型中，随机森林自动评估模型在训练集和测试集中的表现均远远好于BP 神经网络自动模型和支持向量回归自动评估模型；在自动评估模型泛化能力方面，支持向量回归自动评估模型出现了明显过拟合问题，而BP 神经网络和随机森林自动评估模型的表现较为稳定。综合而言，随机森林自动评估模型无论在评估精度还是泛化能力方面均具有明显的优越性。

（三）模型的经济解释

相较于BP 神经网络和支持向量回归自动评估模型的“黑箱”特点，随机森林模型能以节点不纯度或均方误差对变量重要性进行评价，从而识别对房地产价格有重要影响的特征，能够进一步揭示房地产价格的形成机制。随机森林模型对房地产特征重要性的评价如图6所示。房屋面积（area）是决定房地产价格最为重要的因素，距市中心距离（DFC）和绿化率（AR）两个区位因素对房地产价格的影响也颇为重要，紧随其后的是其他区位因素，如物业状况（PF）、教育配套设施（SR）和生活设施（FPF）。总体而言，区位因素对房地产价格的影响程度要高于个体要素，也充分印证了区位对房地产市场的重要性。在影响房地产价格的个别因素方面，住宅楼龄、建筑结构、户型对房价的影响较为重要，而朝向对房地产价格的贡献较小。

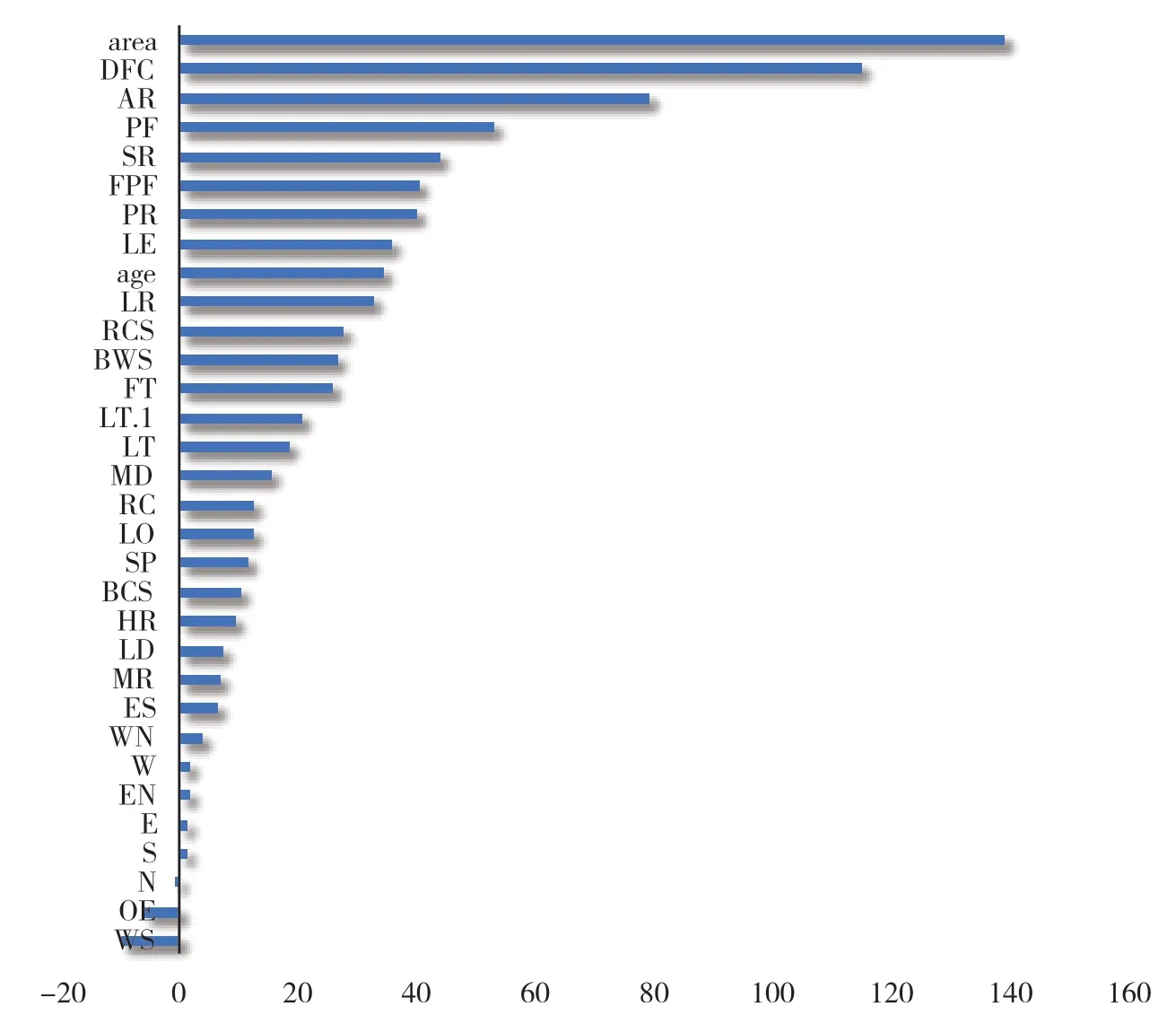
图6 随机森林模型变量重要程度测度

五、结论

在大数据时代背景下，本文以徐州市泉山区和鼓楼区2018年21 590 套二手房首次挂牌案例为样本，探讨了随机森林房地产价格自动评估模型的构建特点，并从评估精度、泛化能力、经济解释三个角度与BP 神经网络、支持向量回归和Hedonic 模型进行了比较分析，得出以下结论：

（1）在随机森林自动评估模型构建过程中，回归树分裂时特征子集的特征个数mtry 对自动评估模型预测精度影响较大，随着特征子集中特征个数的增加，模型的评估效果先迅速增加而后趋于平稳；与之相对，随机森林中回归树的棵数对模型预测效果的影响不显著。

（2）随机森林自动评估模型的预测精度较高，在训练集和测试集中的平均绝对误差百分比为11%，其评估精度显著好于Hedonic 模型、BP 神经网络模型和支持向量回归模型；此外，随机森林自动评估的模型的泛化能力也较好，具有较高的稳定性。

（3）相比于其余机器学习模型，随机森林模型更具经济解释意义，通过变量重要性评价能够进一步揭示房地产价格的构成特征，研究发现区位因素对房地产价格的影响程度要显著高于个别要素，充分印证了区位在房地产市场中的重要性。

当然，本文构建的随机森林自动评估模型也存在一定的局限性。首先，本文构建的自动评估模型反映了样本时段特定的房地产市场结构，若房地产市场结构发生变化，则需重新训练；其次，本文基于同质房地产市场构建随机森林自动评估模型，而现实中一个城市的房地产市场通常由多个同质子市场组成，如何通过模型自动识别房地产市场的异质性特征并将其纳入自动评估模型的构建是未来的重要研究方向。