基于Octave图解计算精馏塔理论塔板数技术研究

叶世贵，李鹏飞，卢宏涛，文 芳，吴孟琪

(中石化广元天然气净化有限公司，四川 广元 628400)

为从多组分体系中分离获得高纯度的产品，通常可以采用多级平衡闪蒸的精馏方式，该方式也是化工单元操作中最重要的一种操作方法[1]。多组分精馏塔可分为简单塔和复杂塔2种，前者仅有一股进料且无侧线出料和中间换热设备，在生产中较为常见。对于二元物料精馏体系，经常面临的一类问题是：已知条件为产品浓度，待求量为理论塔板数。对于二元组分混合物连续精馏，由于仅含有2种组分，一般可通过逐板计算法或图解法求解其理论塔板数[2]。

1 图解法计算原理和过程

1.1 相关方程

对于连续精馏塔(见图1)，塔顶设置全凝器，泡点回流。其气液平衡方程可以表示为相对挥发度α的函数式：

(1)

根据物料衡算可以得到精馏段和提馏段塔板的下降液相组成xn(xm)与进入该层塔板的气相组成yn+1(ym+1)关系式：

(2)

(3)

精馏段操作方程式(2)与提馏段操作方程式3相交得到1个交点，令其坐标为(xq,yq)，则有

(4)

(5)

式4与式5消去参数xD即可得到交点的轨迹方程，称为q线方程，其关系式表示如下：

(6)

1.2 相关数据

用一连续精馏塔分离乙醇-水混合液，原料液中含有乙醇的摩尔分数xF为0.40，要求塔顶馏出液含乙醇摩尔分数xD为0.78，塔釜含乙醇摩尔分数xW为0.02。塔顶设全凝器，泡点回流，所用回流比R为3，试用图解法求进料液相分率q为1.103时的理论板数和加料板位置。已知乙醇-水的汽-液平衡数据见表1。

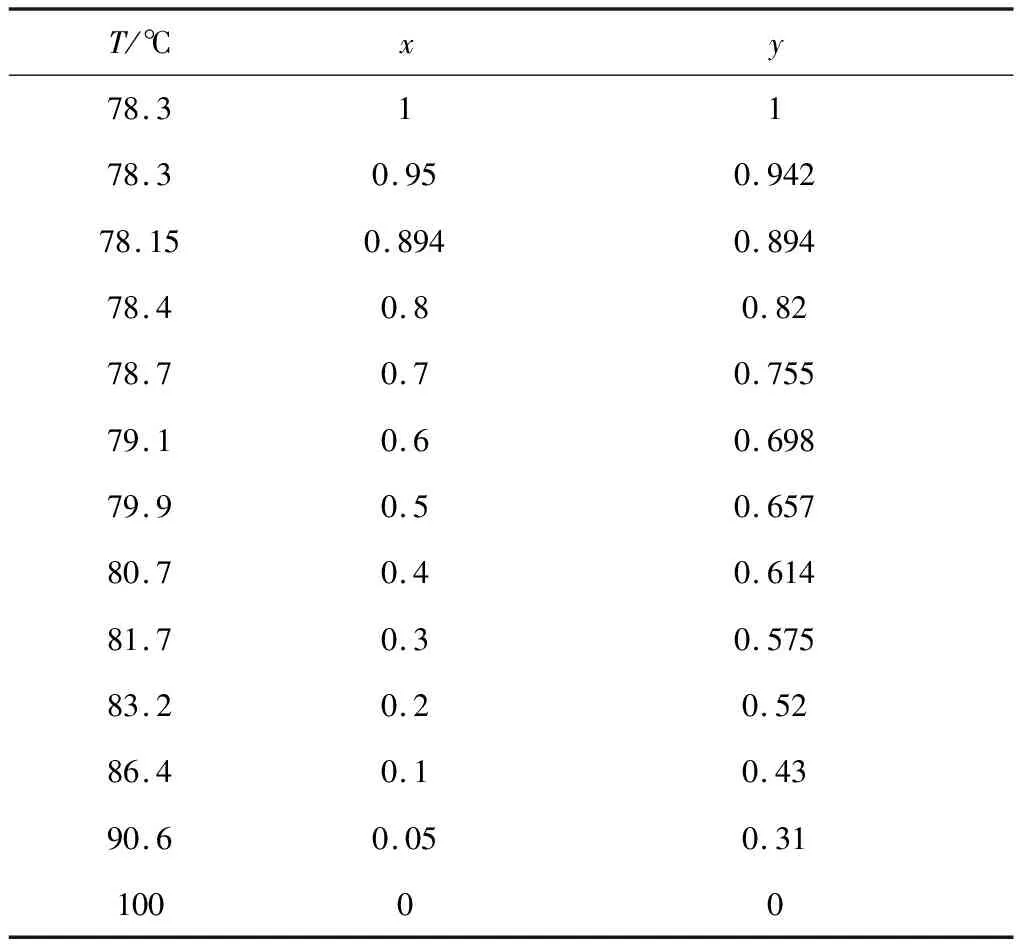
表1 乙醇-水的汽-液平衡数据

1.3 图解手动计算过程

1)相平衡线绘制。按照表1所给的平衡数据可以做出平衡曲线图(见图2)。

4)提馏段操作线绘制。由xW=0.02在对角线上确定点c，连接c、d可得提馏段操作线。

5)阶梯线绘制。从a点开始，在平衡线与精馏段操作线之间做梯级并计数，当梯级与平衡线的交点横坐标小于两操作线的交点d的横坐标时，在平衡线与提馏段之间做梯级并继续计数。当最后一个交点横坐标翻越xW后完成计数，由图2可以得到总理论板数为7，在第5块板进行加料。

2 Octave自动解算及绘图过程

2.1 解算及绘图步骤

1)罗列出所给固定参数条件：xD=0.78，xW=0.02，xF=0.40，R=3，q=1.103。汽液平衡数据赋值给矩阵参数Eqdata。当需要引用所有x值时，可以用Eqdata(1,:)表示，当需要引用所有y值时，可以用Eqdata(2,:)表示。

2)在直角坐标图上使用plot(xD,xD)、plot(xW,xW)定出塔顶组成a点、塔底组成c点。

3)在直角坐标图上使用函数plot(Eqdata(1,:),Eqdata(2,:),'*')绘制汽液平衡点，点的呈现形式为*。

4)通过曲线拟合函数polyfit将散点函数化，其调用格式为：p=polyfit(x,y,n)。该函数采用最小二乘法来对已知数据x、y进行拟合，拟合多项式阶数为n。返回值p为一行向量，长度为n+1，包含了幂次降序的多项式系数，即。拟合完成后，可以使用函数polyval计算多项式的拟合值，其调用格式为y=polyval(p,x)。该函数输入上面产生的一维向量p，返回值y为在x处的多项式计算值。如果输入的自变量x为一矩阵或向量，则返回函数计算多项式在x每一个元素处的拟合值。

5)使用函数plot(x,y)可以绘制出x在0～1范围内，依据拟合产生的汽液平衡曲线。

6)使用函数line绘制对角线。

7)使用fplot函数绘制精馏段方程所表示的操作线，函数以x为自变量，R，xD为固定参数。

8)使用fplot函数绘制q线方程所表示的操作线，函数以x为自变量，q，xF为固定参数。

9)采用数值解法求精馏段操作线与进料线的交点d，调用的函数为fzero，其格式为x=fzero(fun,x0)。其中fun为待求根函数，其具体表现形式为精馏段函数与q线函数相减。fun函数以x为自变量，R，xD，q，xF为固定参数，x0为求解初值。

10)求解出交点后，使用line绘制交点d与塔底组成c点间的直线，即可得到提馏段操作线。

11)从塔顶组成a点开始，在平衡线和精馏段操作线之间绘制梯级。在梯级跨过交点d时，转为在平衡线和提馏段操作线之间绘制梯级，直至梯级跨过c点。此过程中形成的一个三角形梯级表示一块理论塔板，所绘制的梯级总数即为总理论塔板数，过d点的梯级为加料板，最后一个梯级为塔底再沸器。程序化绘制梯级水平线，其原理是为给定y值求解其平衡x值，通过函数fzero解平衡多项式即可得到。绘制梯级的垂直线，为给定x值求解操作线上的y值，通过直接将x带入对应的操作线方程求解即可。

2.2 程序代码

1)设置主函数并储存给定值：

function distillation

clear all;clc;clf;

global xD=0.78 xW=0.02 xF=0.4 R=3 q=1.103;

Eqdata=[

1 0.95 0.894 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.05 0

1 0.942 0.894 0.82 0.755 0.698 0.657 0.614 0.575 0.52 0.43 0.31 0];

2)绘制塔顶组成a点及塔底组成c点：

plot(xD,xD)

text(xD+0.02,xD,'a')

hold on

plot(xW,xW)

text(xW+0.02,xW,'c')

hold on

3)绘制汽液平衡点：

plot(Eqdata(1,:),Eqdata(2,:),'*')

hold on

4)对汽液平衡数据进行拟合：

p=polyfit(Eqdata(1,:),Eqdata(2,:),9);

5)根据汽液平衡拟合函数绘制拟合曲线：

x1=[0.0:0.01:1.0];

y1=polyval(p,x1);

plot(x1,y1)

hold on

6)绘制对角线：

line([0.0,1.0],[0.0,1.0])

7)绘制精馏段操作线：

legend('hide')

recope2=@(x)recope(x,R,xD);

fplot(recope2,[0 0.78],'Color','black')

hold on

8)绘制q线：

qline2=@(x)qline(x,q,xF);

fplot(qline2,[0.4 1],'Color','black')

text(xF+0.02,xF,'f');

hold on

9)求精馏段与进料线交点d：

cross2=@(x)cross(x,R,xD,q,xF);

xc=fzero(cross2,0.5);

yc=recope(xc,R,xD);

text(xc+0.02,yc,'d');

10)绘制提馏段操作线：

line([xc,xW],[yc,xW],'Color','black')

11)绘制梯级并显示总理论塔板数：

axis square

axis([0 1 0 1])

xlabel('x')

ylabel('y')

x0=xD;

y0=xD;

n=0;

while 1

n=n+1;

[x0,y0]=tri(x0,y0,R,xD,p,xc,yc,xW,n);

if x0

break;

end

end

s=sprintf('Total number:%d',n);

text(0.03,0.9,s)

12)自定义精馏段函数：

function y=recope(x,R,xD)

y=R*x/(R+1)+xD/(R+1);

13)自定义进料线函数：

function y=qline(x,q,xF)

y=q*x/(q-1)-xF/(q-1);

14)自定义交点函数：

function y=cross(x,R,xD,q,xF)

y=recope(x,R,xD)-qline(x,q,xF);

15)自定义平衡关系逆运算函数：

function y=inverseop(x,p,yn)

y=polyval(p,x)-yn;

16)自定义动态绘制梯级函数：

function[x,y]=tri(x0,y0,R,xD,p,xc,yc,xW,n)

inverseop2=@(x0)inverseop(x0,p,y0);

x=fzero(inverseop2,x0);

if x>xc

y=recope(x,R,xD);

else

y=yc+(yc-xW)*(x-xc)/(xc-xW);

end

xd=x0;yd=y0;

while xd>x

xd=xd-0.01;

yd=y0;

pause(0.0005)

plot(xd,yd,'r')

hold on

end

while xd<=x & yd>y

xd=x;

yd=yd-0.01;

pause(0.0005)

plot(xd,yd,'r')

hold on

end

text(x-0.03,y0,int2str(n),'VerticalAlignment','bottom','color','red')

2.3 运行测试

将上述代码保存在Octave的运行路径下，如“D:Octavework”，文件取名为distillation.m。在Octave程序命令窗口输入distillation，即可求解并动态绘制精馏塔理论塔板数。运行最终结果如图3所示，该结果与手动绘制结果一致。

2.4 改进方向

本程序为了研究方便，将q值设置为大于1。由于q值可以表征进料加热状态，即q值实际表示进料中饱和液体所占的分率。若进料经预热或部分汽化，其q值较小。当沸点进料时，q=1；当气液混合物进料时，q=0.5；当进料为饱和蒸汽时，q=0。因此程序在使用q线方程前，应该对q值进行判断。1)当q=1时，q线为一条垂直于x轴的直线，其与精馏段的交点d横坐标为xF，纵坐标为xF值带入精馏段操作线方程得出值；2)当q=0时，q线为一条垂直与y轴的直线，其与精馏段的交点纵坐标为xF，横坐标为xF值带入精馏段操作线方程逆向计算得出值；3)当q<0时，若交点在平衡线上或平衡线外，则无解。

设计条件下，如果选用较小的回流比R，则精馏段操作线与提馏段操作线交点往汽液平衡线移动，达到指定分离程度所需的理论塔板数增多，当回流比降至某一数值时，两操作线的交点d落在平衡线上，此时也无解。因此在得出交点d坐标后，应该对该坐标的位置进行判断，若交点在平衡线内方程有解，否则无解。

3 结语

利用Octave开源强大的数据拟合、数值计算和图表绘制等功能，解决了二元物料体系精馏理论塔板数图解计算问题。程序可移植性强，计算精度高，省时省力。自定义动态绘图功能，为方便教学理解图解过程具有重要的意义。改进后的程序，对进料加热状态及回流比适应性更强。