轧制差厚板胀形成形性能
邓淏天,徐应达,陈 婷,付秀娟
武汉工程大学材料科学与工程学院,湖北 武汉 430205
轧制差厚板根据承载载荷设计相应的厚度分布,提高使用性能的同时有效降低了零件的质量。因此轧制差厚板的工业化应用能有效加速航空航天和汽车工业的轻量化进程[1-3]。然而轧制差厚板各厚度区力学性能和塑性变形程度的差异使轧制差厚板在成形过程中易产生应力集中,导致起皱、破裂等成形缺陷的产生[4]。如何提高轧制差厚板的成形性能对于轧制差厚板工业化应用具有重要意义[5-6]。文献[7-9]建立了轧制差厚板拉深时的力学分析模型,研究了轧制差厚板的厚度分布对其力学性能的影响。张华伟等[10-12]通过拉格朗日插值法构造了轧制差厚板的应力-应变曲面,证明了轧制差厚板的应力应变曲线与厚度之间存在一定的联系。文献[13-15]分别建立了轧制差厚板成形性能数值分析模型,研究了轧制差厚板在不同成形方式下的成形性能变化及工艺特点,提出了轧制差厚板工艺优化设计方法。然而轧制差厚板成形性能和成形极限研究的缺失阻碍了轧制差厚板的工业化应用。杯突实验为用球头凸模将周边被凹模与压边圈压住的金属薄板顶入凹模,形成半球形凸起,直至半球形凸起顶部出现裂纹为止,所测量的杯突深度即为杯突值,其杯突值可作为材料的胀形成形性能指标。本文采用杯突胀形实验和有限元数值模拟,研究厚度分布特征对轧制差厚板成形性能的影响规律和破裂机理,建立板料成形极限图,获得提高轧制差厚板成形性能的措施。
1 实验部分
实验材料为Cr340轧制差厚板,板料截面厚度分别为2 mm的等厚区、厚度线性变化的过渡区和1 mm的等厚区,如图1所示。为了对比分析轧制差厚板和等厚板的成形性能和成形极限之间的差异,分别由轧制差厚板和等厚板两种厚度规格的板材制备胀形试样。等厚板胀形试样分别在板厚1和2 mm的等厚区制备试样,分别标记为W1和W2试样,W1和W2试样的长度为90 mm,有效宽度分别为20、25、30、35、40、60、80 mm,如图2所示。由轧制差厚板制备的试样标记为WB试样,在1 mm的等厚区和过渡区制备的试样标记为WB1,在2 mm的等厚区和过渡区制备的试样标记为WB2,试样选取的位置如图1所示,试样尺寸为90 mm×80 mm,等厚区和过渡区的有效宽度均为40 mm。试样尺寸均按照GBT4156-2007国标设计。
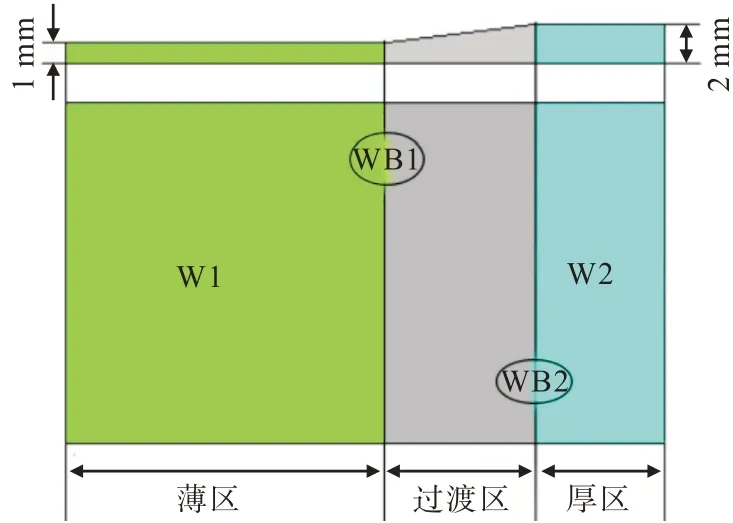
图1 等厚板和轧制差厚板位置示意图Fig.1 Position of blank with same thickness and tailor rolled blank
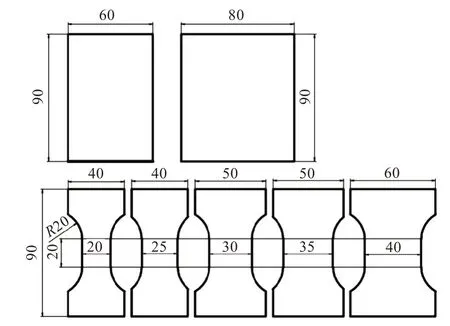
图2 等厚胀形试样突尺寸(单位:mm)Fig.2 Bulging samples size of blank with s ame thickness(unit:mm)
胀形实验前在试样表面印制网格,胀形后选取最靠近破裂处的3处完整网格并测量网格的椭圆长轴长度d1和短轴长度d2,由式(1)获得极限应变,建立成形极限图。其中ε1是主应变,ε2是次应变,d0为初始网格直径。
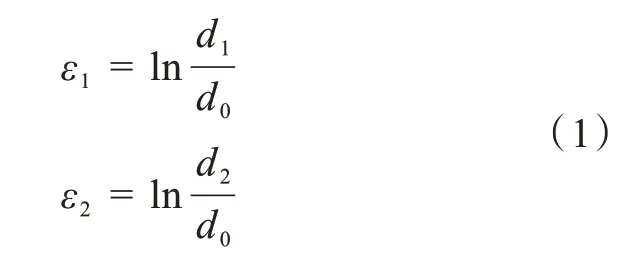
2 结果与讨论
2.1 等厚板胀形实验结果分析
等厚板胀形件形状分别如图3(a)和图3(b)所示,试样杯突值如图4所示。由图3和图4知,由于冲头的挤压作用使裂纹在胀形件顶部产生,且随着试样宽度的增大,其发生破裂时杯突值逐渐减小,这是由于压边力的作用随着有效宽度的增大而增强使板料流动困难所致。

图3 等厚板胀形件:(a)1 mm,(b)2 mmFig.3 Bulging part of blank with same thickness:(a)1 mm,(b)2 mm
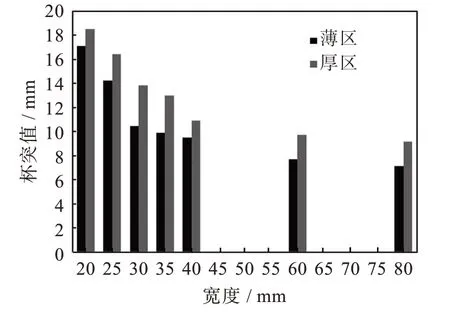
图4 等厚板试样杯突值Fig.4 Erichsen value of blank with same thickness
由图4可知,1 mm和2 mm板料的杯突实验结果进行对比分析,当有效宽度相同时,2 mm试样的杯突值较大。这是因为在压边力等工艺参数不变的情况下,当有效宽度相同时,越厚的试样破裂所需的时间越长,因此其杯突值越大。
1 mm等厚板和2 mm等厚板成形极限图分别如图5(a)和图5(b)所示。散点是进行测量所得到的数据,其中纵坐标是主应变,横坐标是次应变,曲线代表成形极限曲线。由图5(a)和图5(b)可知,其成形极限图中左半部分次应变范围与试样厚度成反比;其杯突值越大,主应变值越大,与主应变轴的截距随着厚度的增加而逐渐增大。
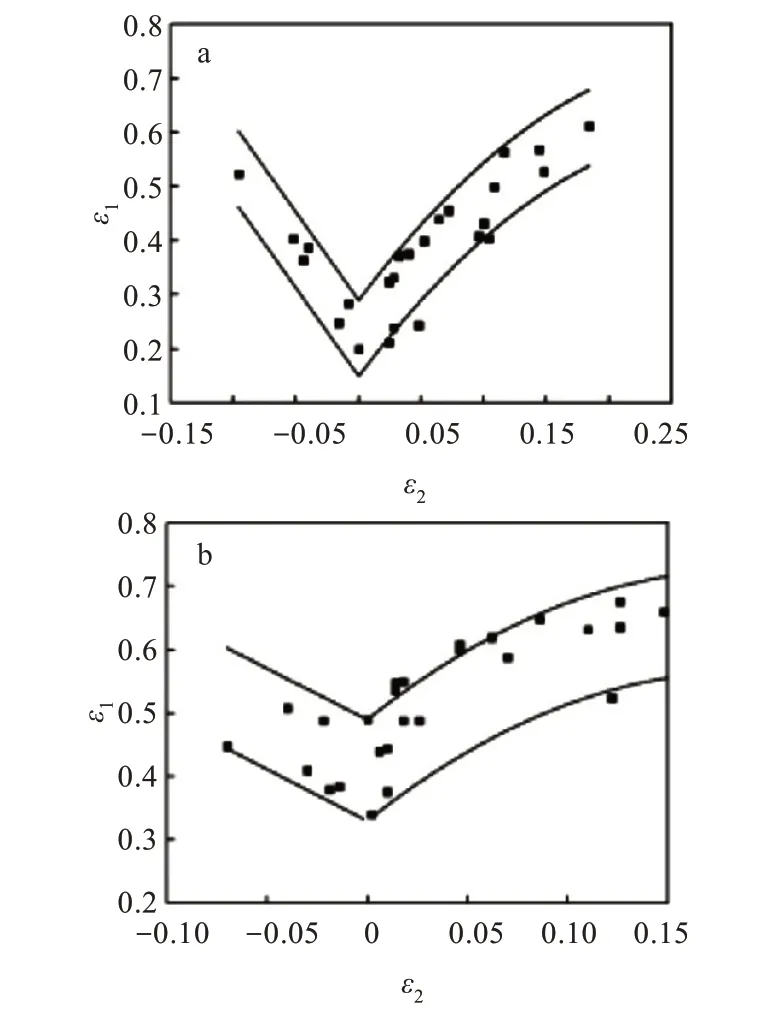
图5 等厚板成形极限曲线:(a)1 mm,(b)2 mmFig.5 Forming limit curves of blankswith same thickness:(a)1 mm,(b)2 mm
2.2 轧制差厚板胀形实验结果分析
宽度相同的等厚板和轧制差厚板胀形件如图6所示。图6(a)为W1型试样胀形结果,其破裂位置在距离顶部2 mm处的圆环区域内产生,裂纹呈由中心向外扩张的趋势,不存在任何偏移量;图6(b)为WB1型试样胀形结果,其破裂位置位于薄区和过渡区的分界线处,且薄侧所产生的颈缩裂纹明显多于过渡区;图6(c)为WB2型试样胀形结果,其裂纹主要处于过渡区内;图6(d)为W2型试样胀形结果,其破裂位于距离顶部2 mm处,各区域的裂纹均匀分布,裂纹并未产生偏移。综上可知,等厚板的破裂一般发生在距离顶部2 mm处,圆环各处的裂纹分布均匀,不存在偏移;而轧制差厚板的破裂一般发生在较薄一侧的区域或两种区域的交界处,随着裂纹的扩展,轧制差厚板的裂纹逐渐向较薄的一侧发生偏移。
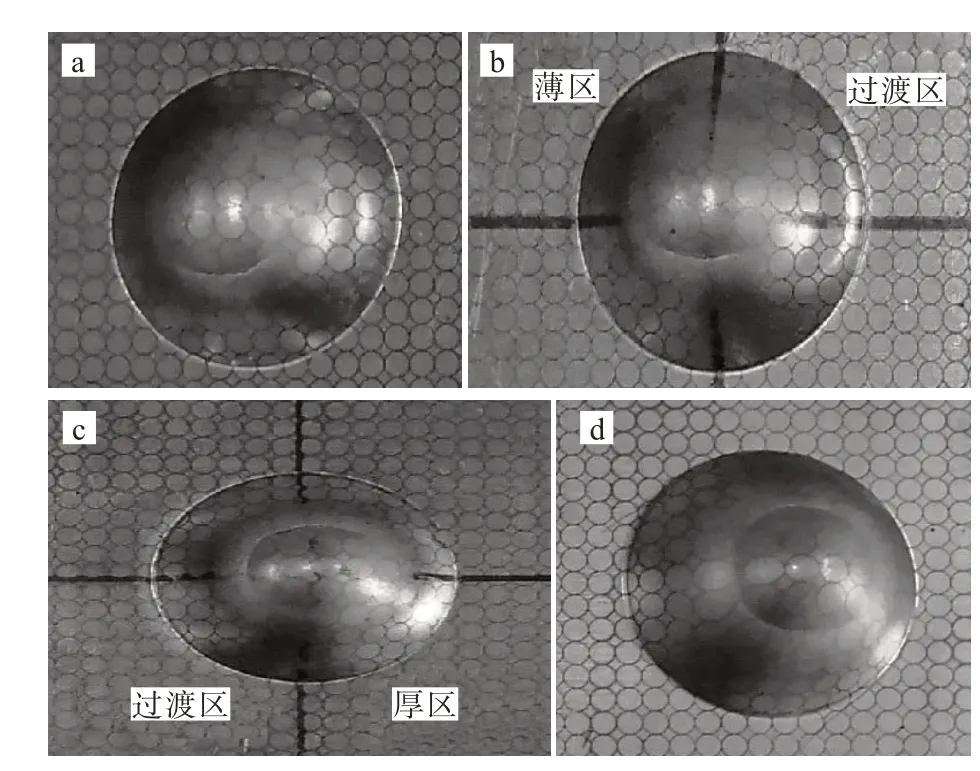
图6 四种板材的胀形结果:(a)W1试样,(b)WB1试样,(c)WB2试样,(d)W2试样Fig.6 Bulging results of four kinds of blanks:(a)W1 type,(b)WB1 type,(c)WB2 type,(d)W2 type
相同宽度等厚板和轧制差厚板试样杯突值如图7所示。由图7可知,相同型号板材杯突值随厚度的增加而增加,表明材料的塑性变形能力有所提高;轧制差厚板与等厚板相比,其杯突值相对较低。
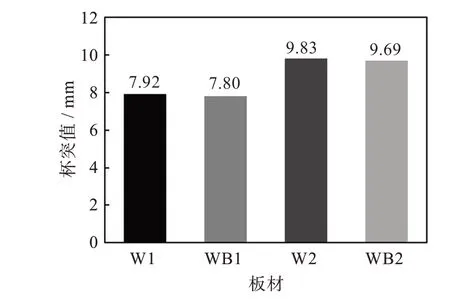
图7 四种板材的杯突值Fig.7 Erichsen values of four kindsof blanks
2.3 轧制差厚板破裂机理
为了分析轧制差厚板成形时的塑性变形行为,采用有限元数值模拟分析了轧制差厚板胀形时的应力和应变分布,模拟结果如图8所示。图8(a)中U3方向的位移值最大为7.108 mm,即表示该试样预测杯突值为7.108 mm,WB1型试样的实验杯突值为7.80 mm,两者相差8%,表明该模拟结果的准确性;图8(b)为WB1试样应力分布云图,薄区出现明显的应力集中,表明裂纹首先在此区域产生,与图8(d)中实验结果相吻合;图8(c)为WB1试样等效应变云图,试样出现颈缩时,轧制差厚板过渡区等效应变大于薄区,且其应变分布不均匀。因此,塑性变形不均匀引起应力集中是降低轧制差厚板成形性能的重要原因,轧制差厚板在成形过程中相比等厚板更容易出现应力集中,其应变分布更加不均匀,降低了轧制差厚板的成形性能。
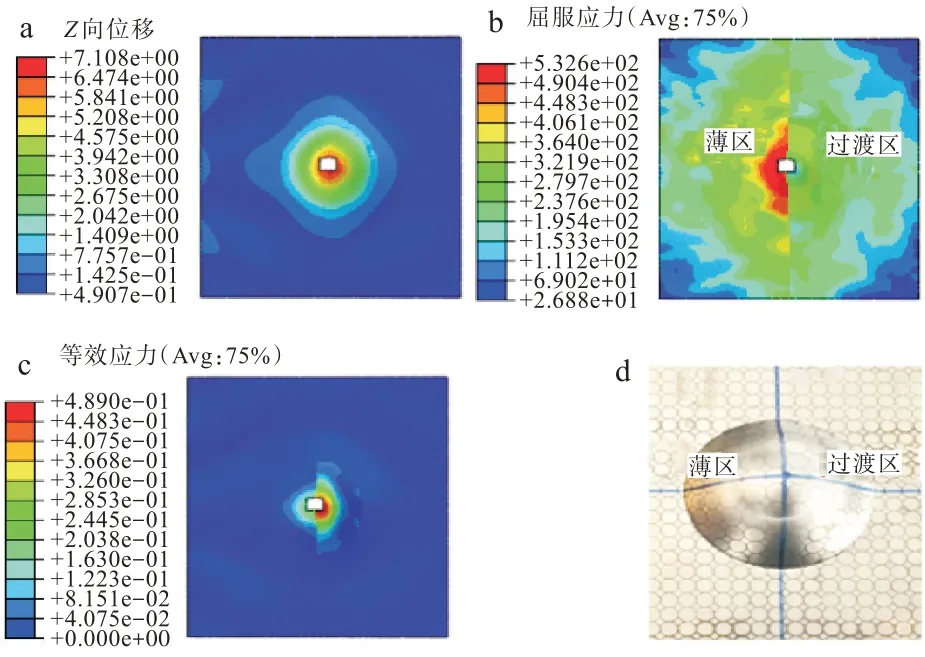
图8 WB1型板材成形预测结果:(a)位移,(b)应力,(c)等效应变,(d)实验Fig.8 Prediction results of forming WB1 type of blank:(a)displacement,(b)stress,(c)equivalent strain,(d)experiment
3 结 论
采用胀形试验探讨了板料厚度分布对轧制差厚板成形性能的影响,进一步应用有限元数值模拟技术分析了轧制差厚板的断裂机理。
(1)通过实验研究了厚度影响轧制差厚板成形性能的规律,相同有效宽度条件下杯突值随厚度的增大而增大;同样厚度试样的杯突值随有效宽度增大而减小,相同规格尺寸下轧制差厚板的杯凸值小于同样最大厚度等厚板的杯凸值。
(2)轧制差厚板的破裂首先发生在较薄一侧的区域或两种区域的交界处,随着裂纹的扩展,轧制差厚板的裂纹逐渐向较薄的一侧发生偏移;相同宽度板材的杯突值随厚度的增加而增加,材料的塑性变形能力有所提高。
(3)数值模拟结果表明轧制差厚板在成形过程中不均匀变形引起应力集中,降低了轧制差厚板的成形性能。

