基于路侧毫米波雷达的车辆碰撞概率计算方法

马小龙，余强*，刘建蓓

(1.长安大学，汽车学院，西安710064；2.中交第一公路勘察设计研究院有限公司，西安710075)

0 引言

事故数据是反应交通安全水平的有力证据，但事故数据存在获取周期长、记录不全面等实际问题。为提升道路交通安全水平，交通管理者需要实时掌握交通流的安全状态，以便及时开展分析决策，因此，探索研究交通事故替代指标成为热点。目前的研究可划分为两方面：一方面，直接从交通流的运行状态入手，即从宏观角度出发，交通流参数与事故数据对照，建立不同交通流安全状态的判定方法；另一方面，从车-车碰撞概率入手，即从微观角度出发，得出两者碰撞的可能性，推导出整个交通流的安全状态。

关于宏观交通流的安全状态判定，目前主要采用事故数据以及交通流运行的微观状态数据，建立事故发生时以及事故发生前两者之间的对应关系，通过大量的数据分析得出危险交通流运行状态判定方法及模型。徐铖铖等[1]基于美国加州I-880N高速公路的交通流和交通事故数据，采用配对病例-对照方法研究事故发生前的交通流特征，具体研究路段长度35 km，线圈平均间隔0.8 km，提出RTCI 实时安全状态判定指标，预测事故精度为65.7%。GU X.等[2]采用无人机视频拍摄的方法，获取高速公路立交合流区的车辆轨迹，基于单一车辆的交通行为，分析合流区的碰撞风险，结果表明合流的速度、驾驶能力以及合流地点对风险水平具有一定的影响。PANDE A.等[3]基于自然驾驶实验采集的GPS 数据，采用负二项回归模型分析发现，路段上紧急制动的比例与该路段长期观测到的事故频率具有很强的相关性，较高的制动减速度与事故具有一定的关联性。

基于交通流运行状态与事故数据的对应关系建立事故发生概率模型，整体预测精度较低，并且对数据的精度以及事故数量具有一定的要求，因此，近年来，学者们转向对安全替代指标的研究。关于安全替代指标，主要分为4 类：时间类、距离类、加速度类以及其他类，4 类指标总计约为20种[4]。朱西产等[5]假定前车以较大制动减速度进行减速，计算出后车驾驶员为了避免与前车发生碰撞的时间余量，将前车以及后车所采用的最大减速度值均选择为0.6g(g为重力加速度)，略小于路面能够提供的最大减速度，认为很少情况下车辆采用最大减速度进行减速。在跟车场景中，最常见的危险情况是前车突然制动，后车如果不及时采取避险措施，则后车很有可能与前车相撞。在这种情况下驾驶员主要采取的避险行为包括：制动、转向以及制动加转向这3种[5]。

关于前车制动减速度的取值，绝大多数研究是假设前车出现较大的制动减速度，计算后车驾驶员经过反应时间之后，与前车发生碰撞的概率。但实际情况是驾驶员采取紧急制动的概率非常小，直接假设前车驾驶员采取紧急制动，最终的计算结果将与实际情况不相符合。为解决该问题，本文采集真实道路上车辆行驶速度，建立不同车型制动减速度的分布模型，从减速度发生概率的角度出发，提出一种新的碰撞概率计算架构。

1 研究对象与数据来源

1.1 路段基本信息

为消除道路几何线形对交通流状态的影响，本文以高速公路直线段为研究对象，开展相关研究工作。路段长度为1 km，3条行车道与1条应急车道，行车道宽度3.75 m。道路中间设有中央分隔带护栏，不受对向行驶车辆影响，按照车辆行驶方向，由内侧至外侧依次命名为1车道、2车道、3车道。1车道与2 车道主要是小客车行驶，外侧第3 车道主要是大型货车行驶。限速范围是60～120 km·h-1，交通量约为35000～40000 veh·d-1，该实验路段距离上游立交入口2 km，距离下游立交出口3 km，该路段没有安装违法抓拍摄像头。实验路段具体场景如图1所示。

图1 实验路段Fig.1 Experimental road

1.2 数据获取方法

在路侧架设3台毫米波雷达与视频融合设备，高度为10 m，平均间隔为300 m。毫米波雷达的频率为77 GHz，最多可同时跟踪256 个车辆目标，数据采集间隔为80 ms，在无遮挡的情况下，最远的有效跟踪距离可达600 m，但在远端部分小客车识别效果较差，为保证数据的有效性，仅分析每台雷达覆盖范围300 m 内的数据。主要利用毫米波雷达进行数据采集，采用视频辅助验证。最终获取的数据包括：时间、车辆编号、车型、坐标位置、速度、加速度，车道位置等参数，数据示例如表1所示。在车辆类型中，1代表小客车，2代表大型货车。

表1 数据样式Table 1 Data style

1.3 数据精度验证

对比分析雷达采集的数据与北斗车载终端采集的数据，验证雷达采集数据的准确性。北斗车载终端的定位精度可达±10 cm，速度精度可达±0.1 m·s-1。图2为北斗车载终端与雷达采集的车辆速度对比部分数据。

由图2可知，雷达采集车辆速度的准确率达到99.1%，此外，通过计算得出跟驰距离精度可达90.3%。

图2 采集速度对比Fig.2 Comparison of speed

2 研究方法

2.1 碰撞概率

在进行车辆碰撞概率计算中，前车是否会采取刹车行为，具有一定的随机性，直接假设前车驾驶员将采取最大的减速度进行刹车，与实际真实情况相差较大，很有可能导致计算结果不准确。针对此问题，本文详细分析了车辆碰撞过程，考虑车辆减速度出现的随机性，提出一种新的碰撞概率计算方法。针对后车追尾前车的不同类型，分3种不同情况进行讨论，车辆行驶状态示意如图3所示。

图3 车辆行驶状态示意Fig.3 Vehicle driving state

第1 种情况，后车在反应时间内与前车相撞，即t≤Δt，计算公式为

式中：Vn为后方车辆n的行驶速度；t为从前车减速到后车与前车发生碰撞的时间；Δt为驾驶员反应时间；Vn+1为前方车辆n+1 的行驶速度；an为后方车辆n的减速度；an+1为前方车辆n+1 的减速度；ΔS为前车发生制动减速时，前车车尾与后车车头之间的相对距离；Sn+1为前车从开始刹车到后车与前车发生碰撞时所行驶的距离。

当前车的减速度符合式(2)时，后车与前车将在反应时间内发生碰撞。随着工况紧急程度的增加，驾驶员更快的释放油门，达到最大踏板刹车压力，当初始车头时距为1.5 s 左右时，即情况紧急下，驾驶员感知反应时间约为1.2 s[6]，王雪松等[6]采用驾驶模拟的方法研究发现，85%的驾驶员在紧急情况下仅通过制动去避撞，因此，对于第1种情况，主要分析在0.0～1.2 s的时间范围内发生碰撞的概率。

第2 种情况，后车经过反应时间后开始刹车，前车还在运动过程中，后车与前车发生碰撞，即

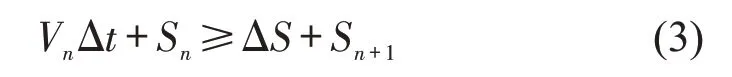
式中：Sn为后车在反应时间之后，与前车发生碰撞时行驶的距离。

前车发生追尾事故时的减速度满足条件为

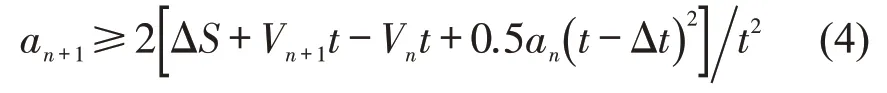
关于发生碰撞的时间长度t，在高速公路上自由换道的时间长度约为6.09 s[7]，因此，以6 s 为上限，在第2种情况下，时间长度t在1.2～6.0 s之间。

第3 种情况，前车停车，后车与前车发生追尾，即

关于后车减速度an，根据实际情况，选择路面能够提供的最大减速度。不同气象环境条件下路面摩擦系数不同，能够提供给车辆的最大制动减速度也有所不同，具体取值需要结合实际情况确定，正常情况下一般取值为0.6 g[5]。

可以得出，计算前后车发生碰撞的概率，关键在于确定前车发生不同制动减速度的概率。根据式(7)求出an+1的最小值，前车减速度大于等于an+1的发生概率即为与前车碰撞的最大概率。不同的t值对应不同的减速度，最小值为

式中：ti为第i时刻。进一步，如果能够建立不同减速度的发生概率，就能够得到后车与前车发生碰撞的概率p，即

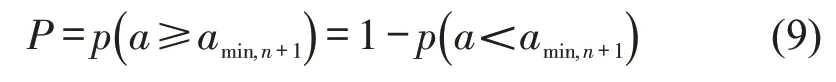
本文以海量的真实观测数据为驱动，首先，研究加速度的特性，并建立该路段车辆制动减速度的分布模型；在此基础上，计算得出后车与前车发生碰撞时前车需要的最小制动减速度，基于分布模型计算出该减速度的发生概率，即得出了前后车辆发生碰撞的概率；最后，综合计算得出整个路段车辆碰撞概率。整体研究架构如图4所示。

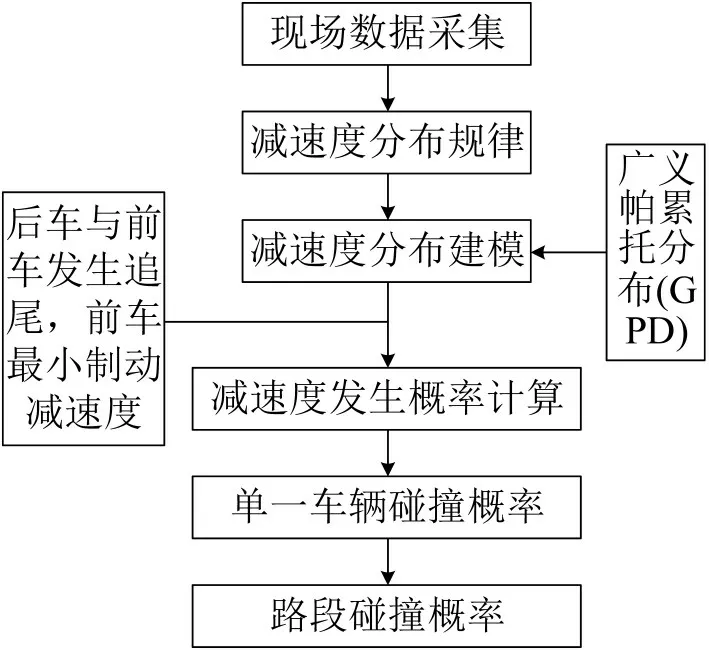
图4 车辆及路段碰撞概率计算流程Fig.4 Calculation chart of vehicle and road collision probability

2.2 制动减速度分布拟合

车辆在高速公路上绝大多数情况下保持匀速行驶，仅在极少数情况下会采取较大的制动减速度，较大的制动减速度往往和交通冲突甚至是交通事故紧密相连，虽然发生概率低，但一旦发生，后果不堪设想。

为更加合理准确地反映此类“极端”数据的特征规律，近年来，在气象、海洋、地震以及保险等领域的学者研究超过某一界限以上的数据的统计性质，即采用超阈值(Peaks Over Threshold,POT)模型处理数据，超阈值可以由广义Pareto 分布(GPD)很好地近似拟合[8]。因此，本文采用GPD模型拟合制动减速度的分布情况。

2.2.1 广义帕累托分布

GPD 模型是经典 Pareto 分布(Pareto Distribution,PD)的一种推广，由Pickands于1975年首次引入[8]，在诸多领域发挥着重要作用，例如，在水文气象领域，对于洪水、风力、气温、降雨等自然现象，均采用GPD 模型进行分析预测。该分布不仅考虑最大值或最小值这类极值数据，更多的是选取超过某界限以上的数据进行研究，因此，GPD 实质上是对超出量的考察，GPD的概率密度函数计算式为

随机变量x的分布函数为

2.2.2 阈值确定方法

（4）The Awakening of the Chinese Patent Dragon-The Revised Chinese Patent Law 2009（中国专利龙的觉醒：中国专利法2009修正案）。

在进行拟合GPD 模型之前，需要确定适当的阈值，以保证超过某阈值的超出量近似服从GPD分布[9]。假设X1≥X2≥…≥Xn是一组样本数据，其尾部可以用GPD 模型拟合，即确定一个k，使得X1≥X2≥…≥Xk可以用GPD 模型拟合，阈值就是Xk。如果阈值选值过大，则超过它的样本量就会减少，而且由于参数对较大的观测数据非常敏感，可能会造成参数估计的方差增大，从而影响估计效果。反之，如果阈值选值过小，虽然可增大样本量，但会出现超出量不服从GPD 的情况，造成估计量为有偏估计。在确定阈值的过程中，经常采用经验平均超出函数法和Hill图法以及百分比法[9]。

平均超出函数法即经验平均超额函数法，假设X1,X2,…,Xn为一系列的观测数值，阈值为μ，则平均超出函数的计算式为

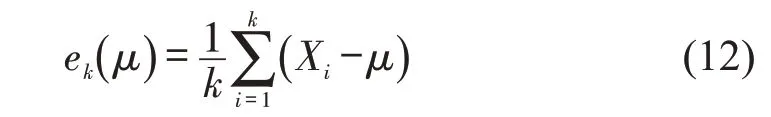
Hill 图法计算过程为：将观测数据按照由大到小的顺序进行排列，即X1≥X2≥…≥Xn，则尾部指数Hill统计量的计算式为

百分位法是将所观测的数据按照升序进行排列，依次选取90%、95%、97.5%、99%百分位的观测值，将其定义为极端参数的阈值[10]。

2.3 参数估计和模型评价

参数估计法采用极大似然估计法(Maximum Likelihood Estimate，MLE)进行估计。关于模型评价，可在不同阈值条件下进行Kolmogorov-Smirnov(K-S)拟合优度检验，将拟合效果最优时对应的阈值确定为最终的阈值。

3 结果分析与验证

3.1 制动减速度分布规律

在数据采集时间段内，车辆行驶状态正常，没有发生拥堵与交通事故，天气状态良好。数据观测时间范围为7:00-20:00，共13 h，观测数据447446组。观测到的加速度最大值为4.4 m·s-2，制动减速度的最大值为-6.0 m·s-2，在区间[-6.0,4.4]之间绘制加速度分布曲线图，结果如图5所示。

图5 车辆加速度分布([-6.0,4.4]m·s-2)Fig.5 Vehicle acceleration distribution map

由图5可知，加速度的分布表现出明显的聚集性，约60.16%的加速度在[-0.1,0.1]m·s-2之间，约99.10%的加速度在[-1,1]m·s-2之间。大多数情况下，车辆匀速通过，绝大多数车辆在行驶的过程中没有采用较大的减速度，即实际发生的交通冲突非常少。

图6(a)为全部的加速度分布情况，图6(b)为加速度局部分布图(加速度分布范围在-1～1 m·s-2之间)。可以看出，3车道的加速度分布最集中，1车道与2车道的加速度分布规律较为类似，主要是由于在3 车道中大型货车尤其是6 轴铰接式卡车比例高，小客车相比于大型车质量小，行驶状态更加灵活，故加速度分布较为离散。在研究中车辆类型主要分为大型货车与小客车，两者约占总数的95%，其中大型货车主要是6 轴铰接式货车，其他车型暂不考虑，不同车型的加速度分布规律如图7所示。

图6 不同车道条件下的加速度分布Fig.6 Acceleration distribution under different lane conditions

由图7 可知，与小客车相比较，大型货车的加速度分布更集中，一方面，大型货车质量大、速度低；另一方面，大型货车司机作为职业驾驶员，行驶状态更加平稳。从制动减速度来看，两者之间具有明显的区别，因此，大型货车与小客车需要区别对待。

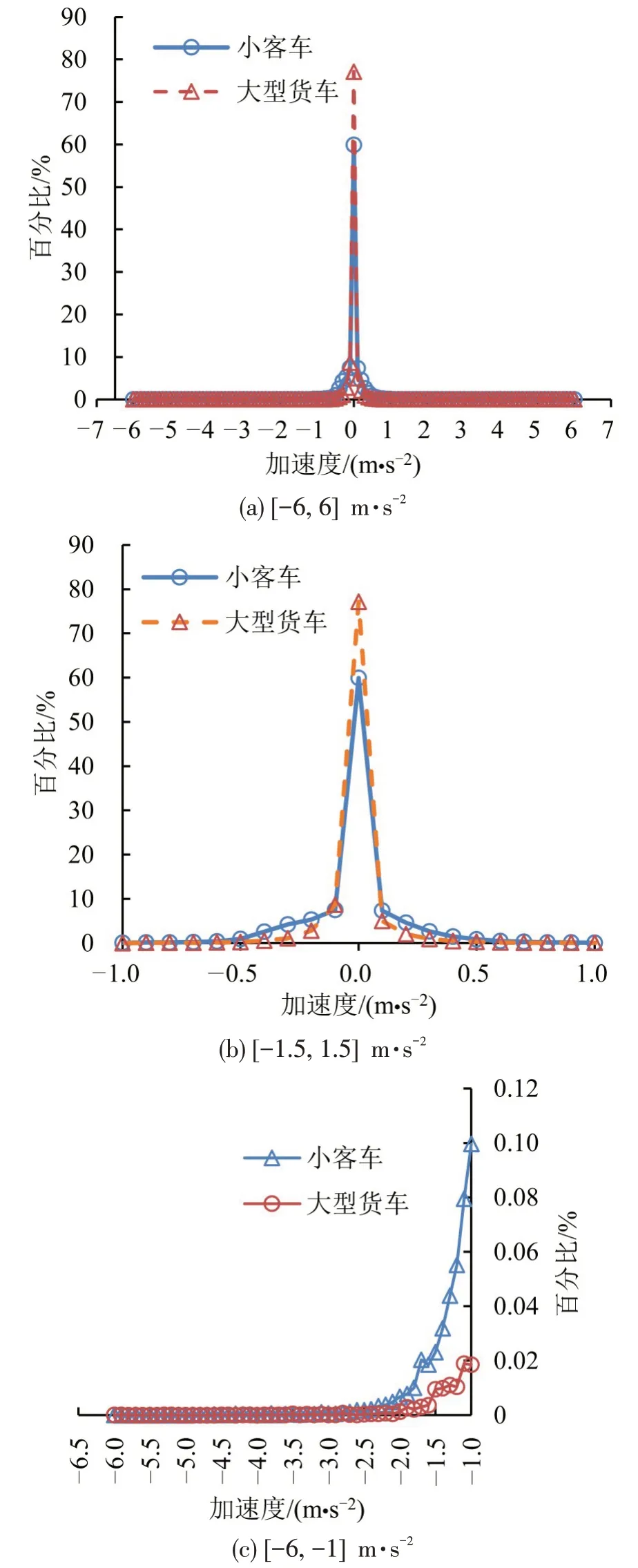
图7 大型车与小客车加速度分布Fig.7 Acceleration distribution of large vehicles and passenger cars

总体来看，车辆制动速度分布表现出明显的“长尾”特征，这种“长尾”分布表明，绝大多数车辆的减速度很小，只有少数车辆的减速度较大。虽然减速度较大的情况发生的概率很小，但发生之后往往会产生严重的交通冲突，甚至造成交通事故，反映出交通事故的罕见性，与实际情况相符，即难以在短时间内观测到大量的交通事故。

3.2 阈值确定与制动减速度分布模型

在高速公路中较大制动减速度，往往和交通冲突甚至是交通事故紧密相关，为客观评估交通流风险水平，必须要掌握车辆制动减速度出现规律，尤其是较大减速度的出现概率，即极值出现的概率。综合采用平均超出函数法、Hill图法以及百分位法确定制动减速度的临界阈值，通常以临界阈值作为阈值μ的估计，平均超出函数法的计算结果如图8所示。

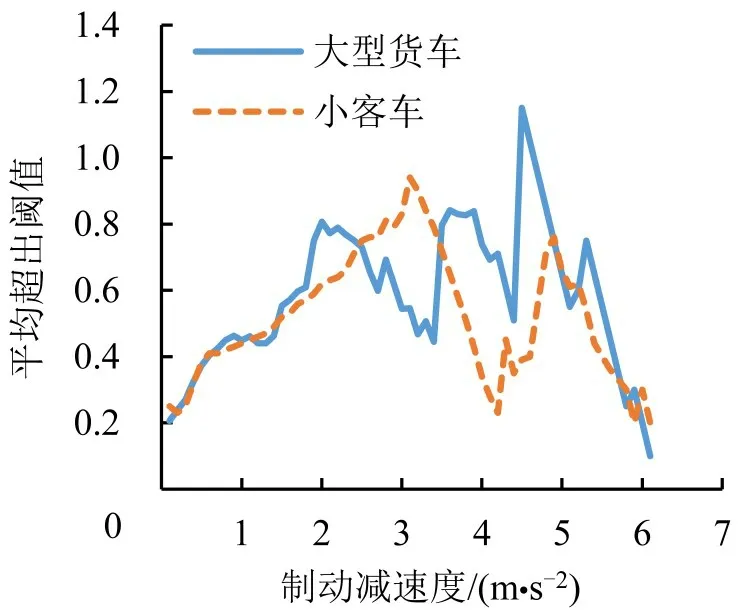
图8 平均超出函数Fig.8 Average exceedance function diagram

由图8 可知，对于小客车，当阈值约在[0.5，1.0]m·s-2区间时，经验平均超出值开始近似呈线性变化趋势，而大型货车的阈值点不是非常明显。小客车Hill计算结果如图9所示。

对于小客车，由图9(a)可知，约在序号1×106附近已经达到稳定。对1×106之前的数据进行局部放大，由图9(b)可知，Hill图尾部稳定区域范围的起始点序号约在0.2×106～1.0×106之间，对应的制动减速度取值为0.4～0.7 m·s-2。大型货车Hill 统计值如图10所示。

图9 Hill统计值(小客车)Fig.9 Hill statistics(passenger car)

对于大型货车，由图10(a)可知，在序号1×105之前已经达到稳定，对0～1×105之间的数据进行局部放大，可以看出，Hill 图尾部稳定区域范围的起始点序号范围约在2×104～4×104之间，对应的制动减速度取值为0.3～0.6 m·s-2。

图10 Hill统计值(大型货车)Fig.10 Hill statistics(Large Truck)

此外，将制动减速度绝对值从小到大的顺序排列，小客车90%、95%、97.5%、99%百分位的观测值分别是0.5，0.6，0.8，1.2 m·s-2；大型货车90%、95%、97.5%、99%百分位的观测值分别是0.3，0.4，0.6，0.8 m·s-2。

在高速公路中，与大型货车相比，小客车的制动减速度波动范围更大，综合上述3 种方法的阈值计算结果，小客车的制动减速度阈值确定为1.0 m·s-2，大型货车的阈值确定为0.8 m·s-2。在此基础上进行参数拟合，计算得出小客车形状参数与尺度参数分别为0.0145、0.429，大型货车的形状参数与尺度参数分别为-0.019、0.458。并且通过K-S 检验。式(11)中的参数标定完成，基于该模型可计算不同制动减速度的发生概率。

3.3 案例验证分析

分别采用真实数据和模拟数据验证碰撞概率计算方法的有效性。

方案1，基于实际采集的跟驰行为数据进行验证，时间长度为53 s，前后车辆均为小型车，行驶速度在80～100 km·h-1之间，最小跟驰距离为16 m，最大速度差为15.44 km·h-1，速度与跟驰距离变化情况如图11所示。

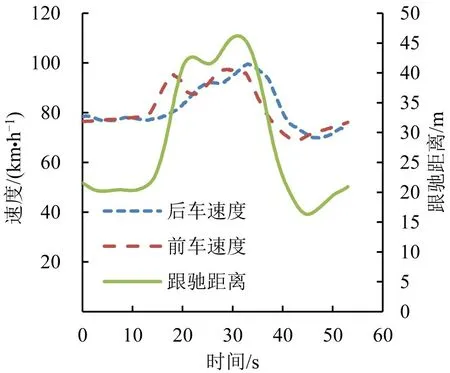
图11 前后车速度与跟驰距离变化Fig.11 Variation of leading and following vehicle speed and car following distance

进一步计算上述场景中的碰撞时间(Time to Collision，TTC)，并将计算结果与本文提出的碰撞概率进行对比分析，结果如图12所示。由图12 可知，本文提出的碰撞概率计算方法的计算结果变化连续，而TTC受相对速度影响较大，尤其是当前、后两辆车速度接近时，TTC 的正负以及绝对值变化剧烈，导致计算结果波动较大，因此，为便于对比，图12 中仅显示-20～30 s 范围内的TTC。对于碰撞概率，在0～15 s 内逐渐下降，约在15～30 s 内，碰撞概率几乎为零。在30～38 s 之间碰撞概率迅速上升，在该时间范围内，后车速度大于前车，跟驰距离逐渐缩小，在37.8 s 的时候，碰撞概率达到最大，之后，后车继续减速，碰撞概率逐渐缩小。当碰撞概率达到最大的时候，TTC 的正值达到最小(7.32 s)，在该时间点两种不同的方法计算结果一致。

图12 碰撞概率与TTC的对比Fig.12 Comparison of collision probability and TTC

XIE K.等[10]提出TTCD(Time to Collision with Disturbance)，并基于3000辆真实的网联车数据，验证了TTCD与追尾事故之间的关联性，并且该指标优于传统的安全替代指标，TTCD 越小，与前车碰撞的可能性越大。碰撞概率与TTCD 之间的对比关系如图13所示。由图13 可知，在TTCD 取值最小的时候，碰撞概率达到最大，并且两个指标所表示的安全状态变化趋势一致，进一步验证了本文提出的碰撞概率的有效性。

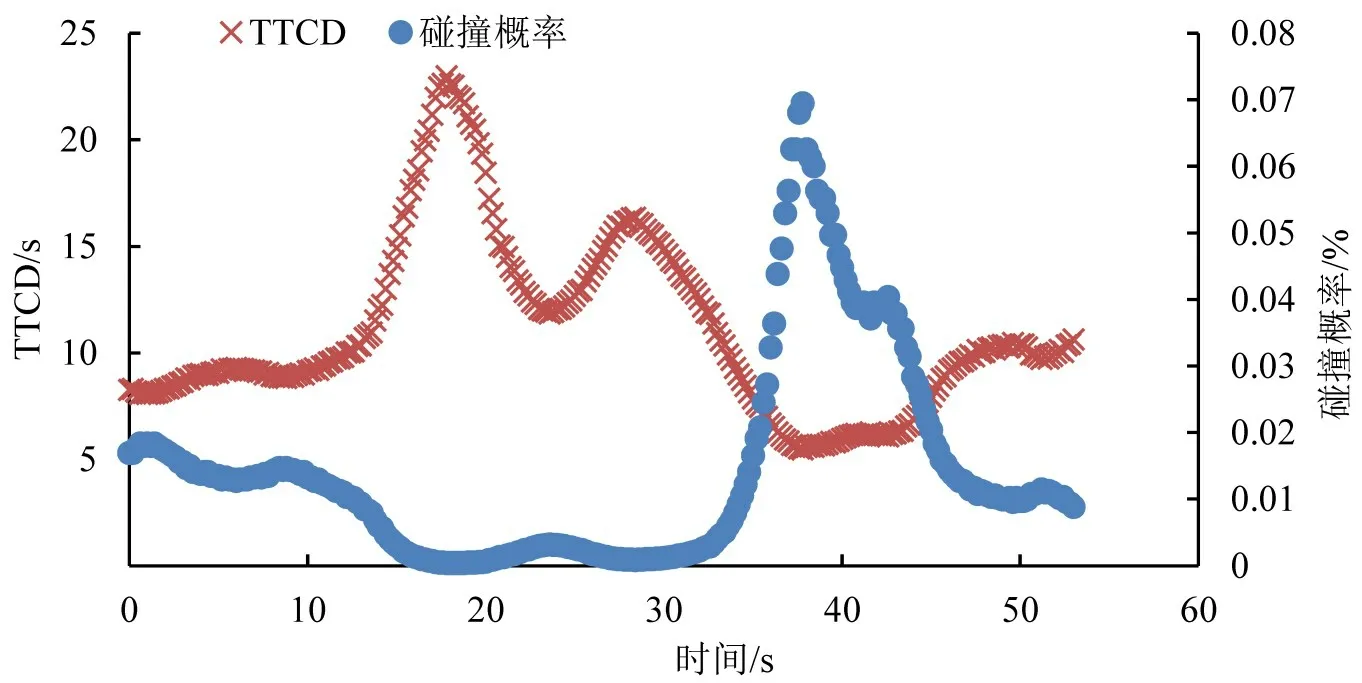
图13 碰撞概率与TTCD的对比Fig.13 Comparison of collision probability and TTCD

方案2，采用模拟数据验证本文提出方法的有效性。固定后车速度为90 km·h-1，控制相对速度变化范围在-10～10 m·s-1之间，分别计算跟驰距离为15 m、20 m 时的碰撞概率以及TTC，需要说明的是每组数据代表1 种典型的场景。计算结果如图14所示。

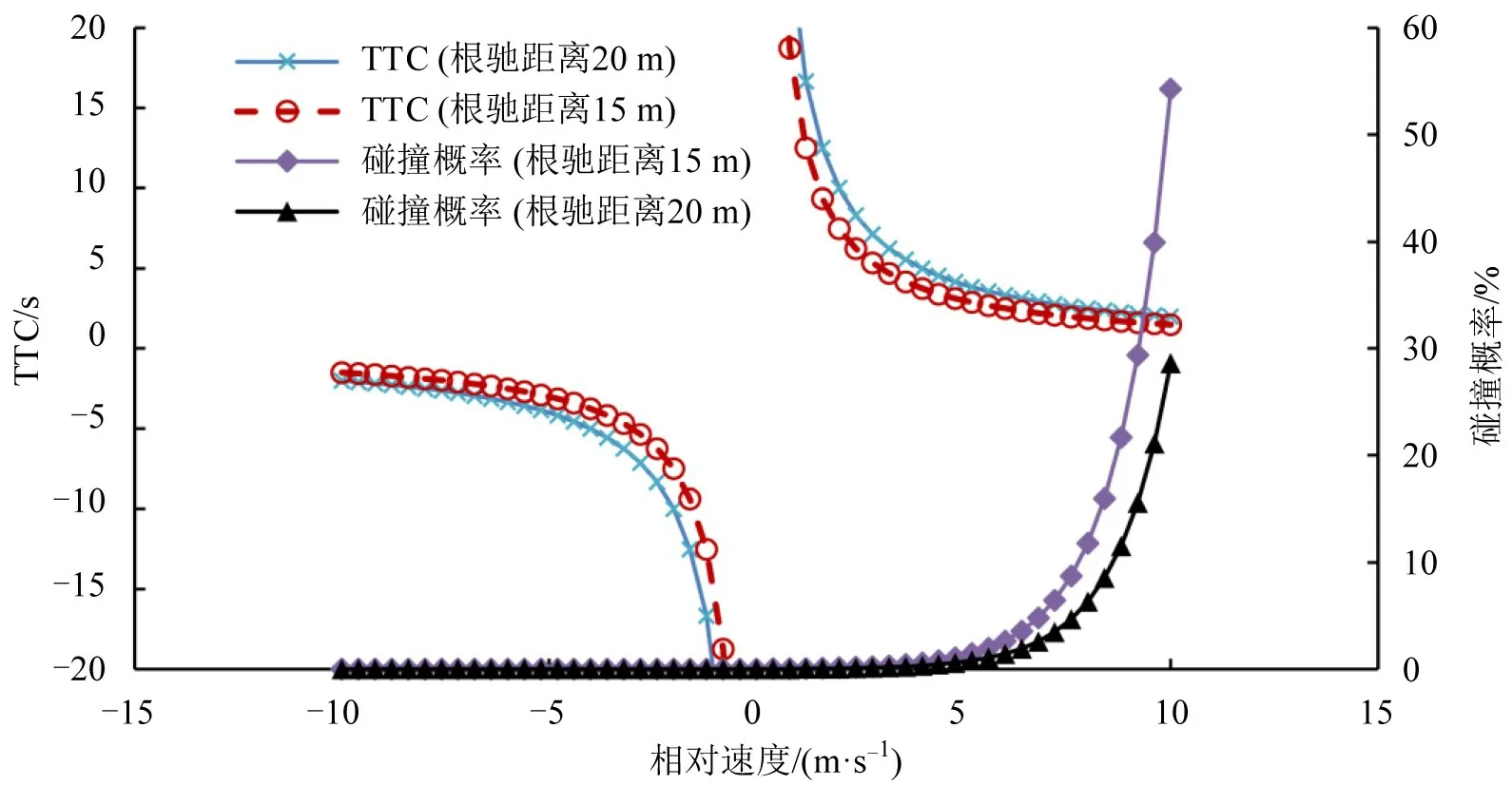
图14 碰撞概率与TTC对比(模拟数据)Fig.14 Comparison of collision probability and TTC(simulation data)

由图14 可知，随着相对速度的增加，TTC 正值计算结果逐渐变小，碰撞概率逐渐增加；跟驰距离越小，TTC 正值越小，碰撞概率越大。当TTC接近2 s 时，碰撞概率迅速上升，碰撞概率最高达到了54.3%，处于非常危险的状态，该计算结果与实际情况相符合。可以明显看出，当前、后车速度接近的时候，TTC 计算值波动剧烈，不能真实反映车辆行驶危险状态，而本文所提计算方法的计算结果连续，可反映不同跟驰距离、不同相对速度状态下的车辆碰撞概率，更重要的是，与传统指标相比较，在危险时刻，本文计算得出的碰撞概率上升速度快，可及时发现危险场景，便于管理者进行决策分析。

4 结论

本文基于路侧高精度毫米波雷达，获得了大量高速公路车辆运行状态实际数据，提出了一种新的车辆碰撞概率计算架构，可在交通安全主动防控领域应用。通过研究得出以下结论：在高速公路平直路段，加速度在[-1,1]m·s-2的区间范围内，占总数据的99.10%，绝大多数车辆以匀速通过平直路段，不同车道以及不同车型的制动减速度分布规律有所区别，制动减速度的分布表现出“长尾”特征，制动减速度符合广义帕累托分布。基于特定路段减速度分布情况，考虑前车减速行为出现的随机性，提出的碰撞概率计算方法，在不同跟驰距离、不同相对速度条件下，计算结果连续，可迅速识别危险场景，实时反映车辆运行安全状态。