考虑多车影响的分子动力学智能网联跟驰模型

宗芳，王猛，贺正冰

(1.吉林大学，交通学院，长春130022；2.北京工业大学，城市交通学院，北京100124)

0 引言

跟驰行为是一种常见的微观驾驶行为，描述了在限制超车情况下，单车道中相邻两车间的相互作用[1]，对车队运行状况、交通流稳定性及道路交通效率有着重要影响[2-3]。因此，跟驰行为建模一直是微观交通流仿真研究的热点问题。随着车-路协同系统中车载设备和路侧设备的不断发展应用，以及智能网联汽车(CAV)智能决策、控制执行相关技术的不断成熟，车-车、车-路、车-人之间实现了信息通信共享，车辆能够获取更多、更精确的实时交通数据[4-5]，其跟驰行为更多地受到周围车辆的影响。其中，研究智能网联汽车的跟驰特性对于交通流运行的稳定控制和拥堵问题的缓解具有重要作用，成为智能交通研究的热点。

在智能网联汽车跟驰建模研究中，学者们主要从CAV跟驰特性研究和基于改进人工驾驶车辆跟驰模型的CAV 跟驰建模两个方面进行研究。在CAV 跟驰特性研究方面，YANG 等[6]将恒定车头时距策略用于描述CAV 跟驰行为，研究交通流的特征，结果表明，CAV 的引入提高了车队的运行稳定性，并且，随着CAV 数量的增加，交通流的稳定性会进一步提高。然而，模型中没有考虑信号延迟对CAV跟驰行为的影响。ZHENG等[7]采用CAV的反馈控制模型模拟混合交通流，发现增加CAV 的数量不仅可以抑制不稳定的交通波，还可以引导交通流达到更高的速度，但是，过高的信号延迟会降低交通流的稳定性。MILANES 等[8]考虑车间距与期望车间距的误差、车间距误差权重、速度差权重及车间距误差微分权重等，提出了协同自适应巡航控制技术(CACC)的跟驰模型。仿真结果表明，CAV的加入可以增强交通流的稳定性，尤其是在交通拥堵时，能够显著提高交通效率。但没有考虑周围车辆对主体车跟驰行为的影响。ZONG等[9]通过考虑多辆前后车的信息和CAV 的延迟时间，提出一种改进的智能驾驶员模型(Intelligent-Driver Model,IDM)，发现不同位置的前车对主体车的影响不同，即前车对主体车运动的影响随着与前车之间距离的增加而逐渐减小。但是该模型采用不同车辆的位置排序粗略地表达对主体车的影响权重，没有定量化的表达不同车辆的速度和与主体车的车间距等因素对主体车的影响程度。

在对人工驾驶车辆跟驰模型的改进方面，XIE等[10]基于智能驾驶员模型，提出一种通用的跟驰模型框架拟合混行车队的跟驰行为，模型考虑了主体车前方车辆的速度、车头时距及速度差等信息，并推导出线性稳定性条件。仿真结果表明，CAV比例的增加可以明显提高路段的通行能力，进而提高交通效率。ZHANG 等[11]通过改进FVD 模型，提出一种CAV 跟驰模型。线性稳定性分析表明，CAV 数量的增加有利于交通流的稳定性，但是该模型并没有考虑不同车辆的速度和车间距对CAV跟驰行为的影响。曲大义等[12]首次应用分子动力学研究了车辆跟驰特性，并对跟驰模型多个刺激项的反应权重进行赋值。数据结果表明，分子跟驰模型能够有效弥补速度跟驰的不足，对跟驰状态的描述更加真实。李娟等[13]基于分子动力学，构建车辆相互作用势，结合刺激-反应模型建立了基于相互作用势函数的分子跟驰模型。仿真结果表明，考虑车辆间的相互作用有利于提高模型拟合精度。但该模型没有考虑主体车的速度差和加速度差等信息，也没有应用实车数据进行参数标定。KNORR等[14]对CAV跟驰模型进行仿真分析，发现CAV 对于交通流运行效率和稳定性都有积极影响。

分析以往研究可知，前后多车行驶状态对于CAV跟驰行为具有一定影响，但多数研究仅考虑多前车相对主体车的位置顺序，而未定量表达前后多车的速度、车头间距、速度差、加速差等参数对主体车跟驰行为的影响。目前，针对这个问题使用分子动力学理论的文献较少，而以往采用分子动力学的跟驰建模研究仅表达了最近邻前车对主体车的影响，而无法考虑多前后车行驶信息进行CAV 跟驰行为建模。因此，本文将在分析CAV 跟驰行为的基础上，构建一种考虑前后多车的速度、车头间距、速度差、加速差等信息的CAV 跟驰模型。应用分子动力学表达周边车辆对主体车的吸引和排斥作用力以及它们对主体车跟驰行为的影响。以期通过基于前后多车信息的跟驰建模，提高车辆的运行效率以及交通流的稳定性。此外，在交通流稳定性分析过程中，本文将考虑CAV 的速度变化对交通流稳定性的影响，更好的再现不同速度情况下真实的交通状态。

1 跟驰建模

本文考虑由CAV 和RV 组成的混行交通流环境。其中，RV车辆在行驶过程中，驾驶人通过直观感受判断前车运动状态及周围行车环境，做出驾驶决策。CAV指能够依靠车载探测设备，路侧传感器以及信息通信技术实时获取前后车的运动状态信息，并通过加速度优化算法进行控制的车辆[15-16]。根据文献[17-18]，前后车辆的信息都会对主体车的跟驰行为产生影响。例如，当主体车与后车的车间距小于安全距离时，主体车往往会加速。这种情况在高速公路的跟驰场景中更为常见。而且，在CAV跟驰建模中，适当地考虑后车对主体车跟驰行为的影响不仅不会产生车辆倒退现象，而且会增加车辆运行的稳定性。原因是：在单车控制方面，主体车考虑后车的运动信息能够提前获得后车的运动状态，进而避免剧烈地加速或减速操作，降低与后车碰撞的危险；在车队控制方面，模型考虑后车的信息对前车影响，能够实现车队更加平稳地运行，这有利于抑制扰动的产生，加快扰动的消散，进而提高整个车队的运行效率和交通流的稳定性[9]。因此，CAV 除了能够实时获得紧邻前后车的速度、车头间距、速度差、加速度等信息，还能获得多前车的速度、加速度等信息。这有利于车辆根据周围行车环境，及时做出跟驰决策。研究表明[9,15]，考虑多前车的信息有利于优化车辆的跟驰行为，提高模型仿真精度。混流环境下CAV跟驰示意如图1所示。

图1 混流跟驰示意Fig.1 Sketch of mixed-vehicles car-following phenomenon

通过分析CAV 的跟驰行为发现，前后车辆的速度、速度差、车头间距和加速度差等信息对CAV跟驰决策产生影响，因此，本文以FVD 模型为基础[19]，提出考虑多前车和1辆后车的车头间距、速度差、加速差等信息的CAV跟驰模型。

根据FVD模型[19]，主体车的加速度由两部分组成。第1部分是最优速度策略，即

式中：α为最优速度敏感系数，与反应时间成倒数关系，反应时间取0.98 s[20]；为最优速度函数，与车头间距有关；是第n辆车在时间t时刻的速度。本文参考FVD 模型的最优速度项，提出考虑多前车车头间距和紧邻后车车头间距的最优速度函数表达式为

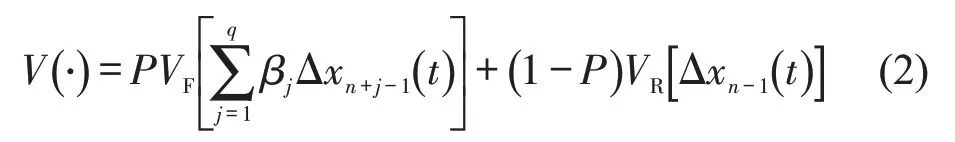
式中：P为前车对主体车的影响权重，0 ≤P≤1；1-P为后车对主体车的影响权重；q为主体车考虑前方所有车辆的数量；为前方第n+j-1辆车与主体车在t时刻的车间距；为紧邻后车与主体车在t时刻的车间距；为前方第j辆车对主体车的权重系数，。文献[21-22]研究表明，不同位置和速度的前车对跟驰车产生不同的影响，多前车的影响不是均匀分布的，需要单独考虑每一辆前车在一定的速度和距离下对主体车的影响。而分子动力学理论[23-24]能够在众多分子中根据分子速度和距离衡量单独两个分子之间的吸引和排斥影响。

因此，为定量表达不同周边车辆对主体车的影响，本文把运动车辆看作分子，利用分子动力学理论计算多前车与主体车间存在的吸引和排斥作用。分子动力学理论认为，随着间距的减小，分子相互间引力逐渐加强，当间距靠近到一定距离以内时，分子相互间会产生强烈的斥力作用。而且，在相同间距下，分子运动越剧烈，相互间产生的作用力越强。前车与跟驰车辆之间的相互作用关系类似于分子间的作用势，当前车与主体车相距较远时，前车有吸引主体车的趋势，且随着两车逐渐接近，引力逐渐减小；而当前车与主体车相距较近时，前车有排斥主体车的趋势，且随着距离缩小斥力逐渐增强。由于不同位置的前车与主体车的距离不同，每一辆前车对主体车的作用势不同，所以，引入分子动力学理论定量表达不同前车对主体车的影响程度。根据分子动力学，赋值方式为

式中：lc为车身长度；V1、V2、C1、C2均为待标定参数，无实际物理意义，为统一函数两侧单位，取V1、V2单位为m∙s-1，C1单位为m-1，C2为无量纲常数[28]；为双曲正切函数。最优速度函数参数的选取依据赵顺[29]的实车标定函数，即设，V1=0，V2=29.5 m∙s-1，C1=0.0229 m-1，C2=0，lc=7.29 m。

第2部分是速度差策略，表达式为

式中：λ为速度差敏感系数，λ≥0；为t时刻周围车辆与主体车之间的速度差。根据FVD模型的速度差项，本文提出了考虑多前车速度差和紧邻后车速度差的表达式为

式中：τ为前车对主体车的影响权重，0 ≤τ≤1；为后车对主体车的影响权重；为t时刻主体车与前方第j辆车之间的速度差；为t时刻主体车辆n与紧邻后方车辆之间速度差。

由于CAV 能够获得周围车辆的加速度信息，因此，本文模型的第3 部分是加速度差策略，表达式为

式中：k为加速度差敏感系数，k≥0；为t时刻周围车辆与主体车之间的加速度差。通过考虑多前车加速度和紧邻后车加速度，的表达式为

式中：ζ为前车对主体车的影响权重，0 ≤ζ≤1；为后车对主体车的影响权重；为t时刻主体车与前方第j辆车之间的加速度差；为t时刻主体车辆与紧邻后方车辆之间加速度差。

因此，主体车的加速度为

当车间距Δxn大于CAV 的最小制动距离s0时，无论多前车加速或减速，CAV 在保证行车安全情况下，都有空间进行相应的加速或减速。此时，CAV不仅受紧邻前车运动状态变化的影响，还会受到其他前车的影响，则，此时CAV跟驰模型为

2 参数标定

利用PATH实验室CAV跟驰RV车辆的实车数据[8]，对CAV 跟驰模型的参数P、λ、τ、k和ζ进行标定。本文参数标定过程中以模型拟合精度最高为目标，以0.01 为步长对所有参数进行遍历寻优。为提高参数寻优效率，本文使用遗传算法增加寻优速度，最终得到拟合精度最高轨迹下的各个最优参数值。根据LI 等[30]的研究，P,τ,ζ取值范围均设定为[0.90，0.99]，λ和k的取值范围均设定为[0.01，0.30]。当P=0.95，λ=0.23，τ=0.93，k=0.08，ζ=0.96 时，CAV 模型拟合图像如图2所示。

图2 CAV跟驰速度-时间图像Fig.2 Velocity distribution of CAV

定量计算该参数下对应的仿真速度和实际CAV 速度之间的误差，并进行单因素方差分析。此时，最大误差为2.44 m∙s-1；平均误差为-0.0041 m∙s-1；R2为99.39%。与其他取值相比，仿真误差最小。通过对该数据进行单因素方差分析，得到此时P-value 为0.98，更接近1 且远大于0.05，F 为0.0030 远小于F crit。数据表明，此时该模型拟合精度最高。

因此，混行跟驰模型中CAV的表达式为

3 稳定性分析

将本文的跟驰模型表达为一般性的模型公式，即

应用一阶泰勒公式，对跟驰模型的一般性模型式(17)在平衡态进行线性化，得

定义平衡态交通流的速度扰动与车间距扰动，分别为

将式(19)～式(21)带入(18)中，计算得到关于扰动的微分方程为

对式(22)进行拉普拉斯变换，得到扰动在交通流传播时的传递函数为

式中：n1为CAV 跟驰模型控制的第n辆CAV；n2为FVD模型控制的第n辆RV。

将式(24)和式(25)转换至频域，即

式中：i 和ω分别为频率域的虚数和频率；。

对两种模型在平衡状态下的速度、车间距、速度差以及加速度差求偏微分，即

将式(28)～式(31)带入式(26)，将式(32)～式(35)带入式(27)可得

根据式(36)和式(37)，分别绘制CAV 跟驰模型和FVD 模型的传递函数在速度区间为0～33 m∙s-1下的幅相特性，如图3所示。

图3 车辆在不同速度下的开环幅相特性Fig.3 Open loop amplitude-phase characteristics of different velocity

由图3(a)可知，CAV跟驰模型的传递函数为闭环系统，且开环幅相特性曲线在右半s 平面没有极点，开环幅相特性平面不包围平面上的(-1,i0)点。所以，根据奈奎斯特稳定判据，得到跟驰模型传递函数在该速度范围内一直是稳定的。图中，三角为模型控制下的交通流阶跃响应震荡方向。通过分析不同速度下的开环幅相特性曲线发现：当速度为0时，幅相特性曲线更接近(-1,i0)点，意味着模型更容易出现阶跃响应震荡，即系统的相对稳定性较低；随着速度的不断增加，幅相特性曲线逐渐远离(-1,i0)点，即模型相对稳定性逐渐增加。原因是：当车辆的行驶速度变慢时，往往会增加短时间内的车流密度，较大的车流量更容易加剧干扰的产生和传播，并在一定范围内增加扰动的幅度，随着时间的增加形成走走停停的波，导致交通拥堵的发生。相反的，在自由流状态下，车辆的速度往往较高，较低的车流量能够抑制干扰的产生，并加快扰动的消散，有利于交通系统的稳定。

由图3(b)可知，FVD模型的传递函数也是稳定的闭环系统。图中，圆点为模型控制下交通流稳定性临界点。通过分析开环幅相特性的频率域特征指标发现，FVD模型闭环系统的稳定程度与速度关系较大，且整体稳定性比混行跟驰模型差。例如，当速度为0 时，对应曲线的截止频率ωc为0.95 rad ∙s-1，相位裕量，对应的时间域指标超调量δ%=1.5%；当速度为20 m∙s-1时，对应曲线的截止频率ωc为0.14 rad·s-1，相位裕量，对应的时间域指标超调量δ小于0.05%。数据表明，随着速度的逐渐增加，时间域指标超调量δ逐渐减小，这表明系统的稳定性逐渐增强；当速度大于20 m∙s-1时，曲线不存在截止频率ωc，即系统达到最稳定状态。另外，当频率ω>ωc时，FVD 模型环幅相特性曲线更接近点，此时，系统的相对稳定性较低；相反的，当ω<ωc时，FVD模型开环幅相特性曲线逐渐远离点，此时，系统的相对稳定性逐渐增强。特别是当稳定闭环系统下的开环幅相特性曲线不存在截止频率ωc时，此时，系统的稳定性最佳。所以，从整体稳定性角度分析，混行跟驰模型的稳定性优于FVD模型。

4 数值仿真与模型验证

4.1 模型验证

目前，美国加州大学伯克利分校PATH 实验室的CACC跟驰模型[31]是较为典型的CAV跟驰模型，该模型结构简单，经过实车验证证明有效，其具体表达形式[8,31-33]为

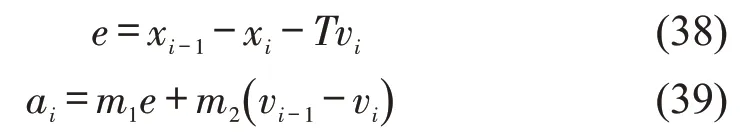
式中：e为实际车间距与期望车间距之间的误差；m1为车间距误差权重；m2为速度差权重；T为设置时间间隔。CACC 模型中，T=1.1 s，m1=0.23，m2=0.07。

为验证所建CAV 跟驰模型与CACC 模型相比在CAV 跟驰行为仿真中的差异性，本文根据上述CACC实车数据，对两个模型进行仿真。两种模型仿真图像如图4所示。

图4 CAV模型验证仿真图像Fig.4 Model verification simulation image of CAV

通过分析两种CAV 模型在相同跟车情况下的仿真图像，发现两个模型的仿真结果都能较好地拟合实际跟车数据。不同的是两个模型在速度达到峰值阶段的加速策略不同。其中，CACC模型在速度即将达到峰值时选择继续加速，保证模型控制下的车辆速度与实际车速相同；在减速过程中当速度即将达到最低速度时，该模型控制下的车辆继续减速，保证仿真速度与实际车速相同。因为CACC模型的加速度控制策略主要是由车间距、速度和速度差决定的，所以，当前、后车的速度差不为0 时，该模型控制下的车辆仍然加速或减速，直到达到期望的最高或最低速度。与上述模型不同的是，本文提出的CAV模型除了考虑速度、车头间距和速度差，还考虑了前、后车的加速度差。通过对比发现，在加速过程中，当速度即将达到峰值时，本模型控制下的车辆并没有选择继续加速，而是降低加速度，特别是在实际车速抖动较大的情况下，仿真车辆的加速度策略更加平缓；在减速过程中，当速度即将达到最小值时，仿真车辆逐渐降低减速度，使整个减速过程更加平稳。为了对比两种模型拟合的精度，本文计算了CACC模型仿真数据与实际数据的相关误差。其中，最大误差为2.63 m∙s-1，平均误差为-0.0056 m∙s-1，均大于本文CAV 跟驰模型的最大误差2.44 m∙s-1和平均误差-0.0041 m∙s-1。同时，该模型的R2为98.48%，小于本文CAV 跟驰模型的99.39%。通过对比发现，相较于CACC 模型，本文建立的CAV 混行跟驰模型在实车数据拟合方面效果更好。

4.2 数值仿真

4.2.1 混行交通流基本图

本文考虑由CAV 和RV 组成的混行交通流环境。其中，采用FVD 模型和本文提出的CAV 模型分别描述RV 和CAV 的跟驰行为。当交通流稳定时，式(16)中每一辆车的加速度，速度差和加速度差均为0；每一辆车的速度相等且均为vˉ，单位是m∙s-1。此时，混行交通流稳定状态下RV和CAV的车头间距为

假设混行车队中共有N辆车，RV 的比例为P′，CAV的比例为Q，且P′+Q=1。那么混行交通流稳定状态下的平均车头间距是RV 和CAV 车头时距的线性平均值，即

根据交通流密度与平均车头间距之间的关系，稳定状态下的混行交通流密度为

式中：K为稳定状态下混行交通流的密度(veh·km-1)。

将式(40)和式(41)代入式(42)，得到稳定状态下速度与混行交通流密度的关系为

类似地，根据交通流量、密度和速度的宏观交通流关系得到交通流量和速度之间的关系为

(veh·h-1)。

根据式(43)和式(44)，分别得到不同CAV 比例下的RV和CAV混行交通流的基本图，如图5所示。

图5 不同CAV比例下的RV和CAV混行交通流的基本图Fig.5 Fundamental diagram of traffic flow mixed with RV and CAV under different CAV penetration

通过分析不同CAV 比例下混行交通流的基本图发现：随着CAV比例的逐渐增加，相同交通流密度情况下车队的平均速度和交通流量逐渐增加。原因是：CAV 跟驰模型不仅考虑紧邻前车的信息，还能获得多前车和后车的运动信息。车辆在模型的控制下能够获得整个车队的运行趋势并提前做出有效的跟驰决策，达到平稳的运行效果，有利于降低周围车辆对主体车的干扰强度，加快扰动的消散，进而提高车队的速度和运行效率，增加交通流量和交通流的稳定性。

4.2.2 迟滞回环

迟滞回环是由不同车头间距下交通流运行时最大及最小车速所围成的曲线。在回环上的相同横坐标的两个点分别表示当车头间距为某个值时，交通流的可能最小及最大速度。迟滞回环的大小可以表征非线性情况下交通流的稳定性，迟滞回环越大，交通流系统的稳定性越差，受到扰动后的波动越大；反之，交通流越稳定,交通流的波动越小。CAV 模型与FVD 模型的迟滞回环曲线如图6所示。

图6 迟滞回环曲线Fig.6 Hysteresis loops for FVD model vs CAV model

通过分析发现：在相同车头间距情况下，CAV模型控制下交通流的最低速度和最高速度均高于FVD模型，即CAV模型控制下的车队速度更快，运行效率更高。同时，CAV模型迟滞回环曲线的面积小于FVD 模型迟滞回环曲线的面积，表明CAV 模型控制下的交通流稳定性更强。原因是，相比较FVD 模型，CAV 模型不仅考虑了多辆前车和后车的速度、速度差、车头间距和加速度差等信息，同时，应用分子动力学理论，定量表达了每一辆前车对主体车的影响程度。因此，CAV模型控制下的车辆能够提前获得整个车队的运行状态，从而更加平稳的进行加速或减速。

5 结论

本文提出了一种适用于CAV 的考虑多前车和1辆后车的车头间距、速度差、加速度差等信息的跟驰模型。应用分子动力学理论，模型引入参数βj，利用不同前车的速度和它们与主体车的车间距定量化计算每一辆前车对主体车的影响权重。仿真结果表明，利用分子动力学理论考虑前后多车的速度和车间距等信息，模型能够更加真实地反映周围车辆对主体车跟驰行为的影响。同时，考虑前后多车的信息，有利于提高车辆的运行效率以及交通流的稳定性。根据稳定性分析结果，CAV跟驰模型控制下的车辆比FVD 模型更加稳定。此外，本文还研究了速度对模型稳定性的影响。结果表明，当车辆的行驶速度较慢时，往往会增加短时间内的车流密度，较大的车流量更容易增加干扰的产生和传播，并在一定范围内增加扰动的幅度，随着时间的增加形成走走停停的波，导致交通拥堵的发生。相反的，在自由流状态下，车辆的速度往往较高，较低的车流量能够抑制干扰的产生，并加快扰动的消散，有利于交通系统的稳定性。相比较FVD模型，CAV 跟驰模型在一定范围内能够接收更多前车的信息，车辆提前获得整个车队的运行趋势，并做出更加有效的跟驰策略，达到平稳运行的效果。这有利于降低周围车辆对主体车的干扰强度，加快扰动的消散，从而提高了整个交通流的稳定性。

模型验证结果表明，与CACC 模型相比，本文建立的CAV 跟驰模型的最大拟合误差为2.44 m∙s-1，平均误差为-0.0041 m∙s-1，相较于CACC 模型的最大误差和平均误差分别减小了7.78%和26.79%，拟合精度提高了0.91%。原因是，本文提出的CAV 模型除了考虑速度、车头间距和速度差，还考虑了多前车和紧邻后车的加速度差。结果表明，在加速过程中，当速度即将达到峰值时，本模型控制下的车辆并没有选择继续加速，而是降低加速度，特别是在实际车速抖动较大的情况下，仿真车辆的加速度策略更加平缓。同样的，在减速过程中，当速度即将达到最小值时，仿真车辆逐渐降低减速度，从而使整个减速过程更加平稳。

仿真结果表明，在由CAV和RV组成的混行交通流环境中，随着CAV比例的逐渐增加，相同交通流密度情况下车队的平均速度和交通流量逐渐增加。同时，相比较FVD模型，CAV模型迟滞回环曲线的面积更小，因此，该模型的稳定性更强。

在目前CAV 实车实验受限的条件下，可采用本模型进行混行交通流中CAV 跟驰行为仿真，为未来混行交通流场景下的车辆控制及交通设施规划设计等提供理论依据和模型基础。此外，本文所建立的模型可应用于由CAV组成的均质流或CAV和RV任意排列所组成的混行车队的队列控制。