内外贸同船运输下长江经济带穿梭巴士网络优化
彭子烜,于滨
(1.北京交通大学,交通运输学院,北京100044;2.北京航空航天大学,交通科学与工程学院,北京102206)
0 引言
2020年长江干线货物通过量为30.6 亿t,同比增长超4.4%,干线港口集装箱吞吐量达2000×104TEU,长江经济带成为推动国内、国外双循环的重要通道。在有限的运力资源下,内外贸同船运输需求日益旺盛,正逐渐改变长江经济带集装箱运输网络的布局。
在以往的长江经济带集装箱运输中,内贸和外贸货物运输相互独立,各自经营。在需求低迷期,船舶舱位利用率不足,降低服务频率将导致无法与干线大船班期合理衔接;在需求旺盛期,运力资源有限,即使船期排满,仍无法满足运输需求。而内外贸同船运输模式的提出有效地解决了以上困境。内贸和外贸货物可由同一艘船舶运输,避免了舱位资源的浪费;同时,内贸和外贸货物运输需求相互补充,避免了单一贸易运输类型带来的不确定性和波动性。因此,充分利用内外贸同船运输政策优势,优化长江经济带穿梭巴士网络,是降低运输成本和碳排放,提高运作效率的重要途径之一[1]。
在穿梭巴士网络优化方面,一类研究关注于内河穿梭巴士网络优化以链接海港,例如,CARIS等[2]以安特卫普港为服务对象,构建基于非线性整数规划的穿梭巴士网络优化模型,模型约束主要考虑了流量平衡约束。ZHANG 等[3]研究了基于枢纽港的穿梭巴士网络,考虑船队的经济规模和船型,以最小服务成本为目标建立双层优化模型。另一类研究围绕港口运营问题,派遣穿梭巴士出港,例如,FAZI等[4]以最小化运输成本为目标,优化从港口到腹地的集装箱运输问题,模型中考虑了流量平衡约束、船舶载重约束和返回时间约束等。相关综述类研究可参考BU 等[5],在已有的穿梭巴士网络研究中,大多以运输成本最小化或收益最大化为目标,考虑流量平衡、服务时间、船舶载重和需求满足等约束,进行基于往返的单航次优化。
在长江经济带集装箱运输网络优化方面,国内外学者进行了一系列研究。宫之光等[6]以长江上游出口集装箱运输为研究对象,构建考虑水运、陆运、海运和换装的超级网络,以运输费用最小为目标,优化设计集装箱网络。陈琛[7]通过长江航运大数据预测长江干线短期货运量和船舶在港停留时间,分别对长江干线班轮进行航线优化和船期优化。杜剑等[8]以班轮航线期望周期运营成本最小化为目标设计航线,考虑了承诺到港时间,并通过模拟仿真进行求解。NOTTEBOOM 等[9]从地理、宏观经济、制度等方面对长江经济带和莱茵河的集装箱网络进行了比较实证分析。YANG 等[10]建立整数规划模型优化长江经济带的集装箱网络,同时优化航线,挂靠港口及挂靠顺序和船舶配置。优化结果建议在长江中游使用大船,在上游和下游使用小船。ZHENG等[11]设计了长江经济带轴辐式内贸集装箱网络,研究结果符合长江经济带货物集中化和港口区域化的趋势。
上述研究多基于内贸集装箱或外贸集装箱运输进行网络优化,考虑内外贸同船运输模式的研究较少。在模型构建方面,大多数研究从单航次角度进行网络优化。本文松弛了内贸货物和外贸货物不能同船运输的约束,考虑可拆分的运输需求,并且保证每个港口的访问频率,构建内外贸同船运输政策下,轴辐式长江经济带穿梭巴士网络优化模型,优化一定周期内船舶多航次运输。并以长江经济带干线港口为例,对内外贸同船运输政策的经济效益及内外贸同船运输政策实施后,穿梭巴士网络结构的变化进行分析,为长江经济带干线港口发展提出建议。
1 问题描述与建模
1.1 问题描述
内外贸同船运输如图1所示。以图1中的例子对基于内外贸同船运输的穿梭巴士网络优化进行说明。如图1(a)所示,该例子中包含2 个内河港口1、2 和1 个海港3,仅考虑运输时间,从港口1 到港口2 的运输时间为2 d,从港口2 到港口3 的运输时间1 d,规划周期为1 周。从港口1 到港口3 的内贸集装箱运输需求为10 TEU,外贸集装箱运输需求为20 TEU,从港口2到港口3的内贸集装箱运输需求为30 TEU,外贸集装箱运输需求为90 TEU。假设穿梭巴士最大载箱量为80 TEU。传统的小型船舶内贸和外贸货物不能同船运输,需安排不同的船舶分别进行承运,如图1(b)所示。穿梭巴士1 装载20 TEU 外贸集装箱从港口1 到港口2,在港口2 装载40 TEU 外贸集装箱,于第3 天将60 TEU 外贸集装箱运抵港口3。穿梭巴士1 返回港口2,装载50 TEU外贸集装箱,于第5天运抵港口3。同理,穿梭巴士2 装载10 TEU 内贸集装箱从港口1 到港口2,在港口2 装载30 TEU 内贸集装箱,最终,将40 TEU内贸集装箱运抵港口3。
当内外贸货物可以同船运输时,可由1艘穿梭巴士完成承运,如图1(c)所示。10 TEU内贸集装箱和20 TEU外贸集装箱同时在1港装船,穿梭巴士1到达2 港后,装载40 TEU 外贸集装箱,穿梭巴士1继续将内外贸集装箱运至3港。穿梭巴士1返回港口2,装载30 TEU 内贸集装箱和50 TEU 外贸集装箱,运抵港口3。内外贸同船运输模式可以节约运力,提高舱位利用率,有利于加快货物的中转。
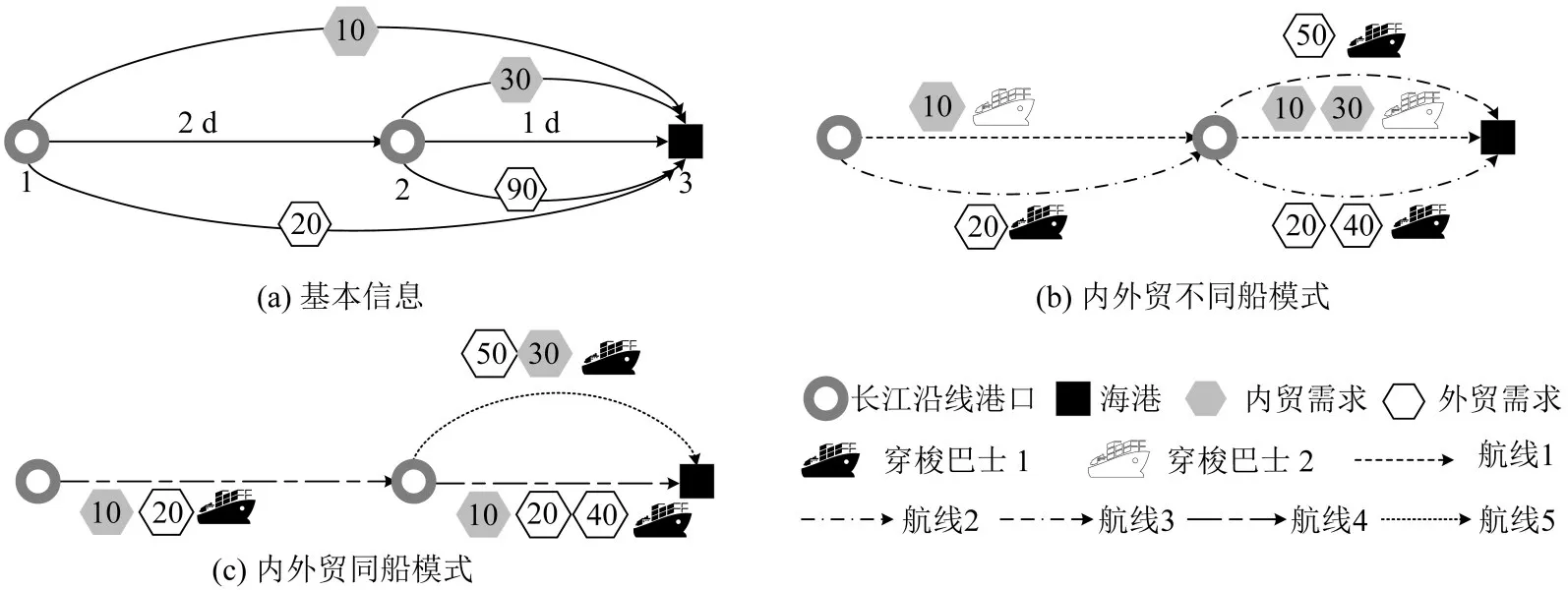
图1 内外贸同船运输示例Fig.1 Case of waterbuses engaging in domestic and foreign trade
1.2 模型构建
本文基于内外贸同船运输政策,以上海港为外部交换海港,进行从上海港和各长江经济带干线港口间的内外贸集装箱运输,优化长江经济带穿梭巴士网络。该问题等价于可拆分的车辆路径问题的变形,模型的目标函数为最小化运输成本,考虑服务频率、服务时间、转运等约束条件,优化1个周期内多艘船舶的多个运输航次。模型部分应用的变量及参数如表1所示。

表1 模型变量及参数Table 1 Variables and parameters
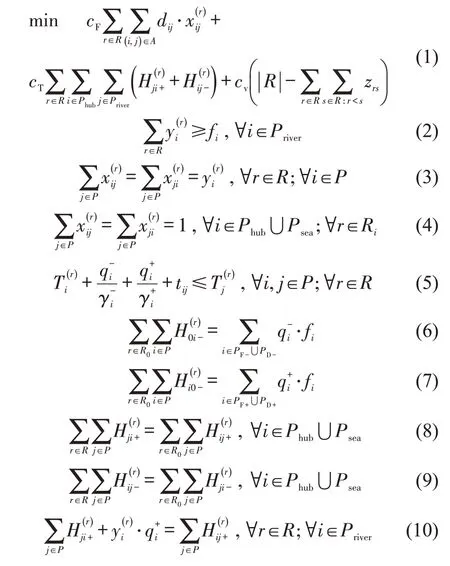

式(1)为目标函数,使运输总成本最小化,包括:燃油成本、转运成本和固定运营成本;式(2)表示航线服务频率应满足港口频率要求;式(3)和式(4)为路径平衡约束;式(5)表示穿梭巴士到达港口的时间;式(6)~式(11)为集装箱流量平衡约束;式(12)表示穿梭巴士的载箱量不能超过船舶载重量;式(13)表示从枢纽港出发的航线可以到达下一个枢纽港或其分配的支线港;式(14)表示在规划周期内经营航次;式(15)和式(16)为转运约束;式(17)表示当两个航次由同一艘船舶运营时,后一航次的开始时间不能早于前一航次的结束时间;式(18)和(19)表示同一船舶运营航次约束;式(20)表示总航线长度不能超过最大限度。
2 算法设计
大邻域搜索(LNS)算法是一种基于破坏和再修复机制的启发式算法。在LNS 的基础上,学者Ropke 和Pisinger 在一次迭代中考虑选择多个破坏和修复算子,破坏和修复算子被选择的概率取决于算法的权重,提出了自适应大邻域搜索(Adaptive Large Neighborhood Search,ALNS)[12]。本文模型是可拆分车辆路径问题的变形,虽然可以通过Cplex等求解软件进行求解,但是仅限于小规模算例。因此,本文设计自适应大邻域搜索算法求解该问题。自适应大邻域搜索算法的基本框架如图2所示。

图2 自适应大邻域搜索算法框架流程Fig.2 Framework of adaptive large neighborhood search algorithm
本文采用贪婪算法生成该问题的1 个可行解。在邻域搜索阶段,本文设计了5个破坏算子和2 个修复算子。每个算子被选择的概率正相关于该算子当前的权重。在一次邻域搜索迭代中,随机确定当前解的qI个中间港口,以及qS个始发港(枢纽港或海港),根据破坏算子规则从当前解中提取出来。然后,把这些港口按照选择的修复算子重新插入到当前解中,形成1 个新的可行解。最后,根据每个破坏算子和修复算子的表现,更新所有算子的权重,为下一次迭代选择哪些算子提供参考。初始化每个破坏算子di和修复算子ri的表现得分为0,在每一次邻域搜索迭代中,如果破坏算子di和修复算子ri被选择并产生了1 个新的可行解,那么算子的得分和取决于产生的新解S′的状态:
(1)若新解S′优于目前最优解Sbest,则算子di和ri的得分增加θ1;
(2)若新解S′劣于目前最优解Sbest且优于当前解S,则算子di和ri的得分增加θ2;
(3)若新解S′劣于当前解S,但被模拟退火准则接受,则算子di和ri的得分增加θ3;
(4)若新解S′未被接受,则算子di和ri的得分不变。
假设θ1>θ2>θ3,经过qI+qS次邻域搜索迭代后,算子di(或者ri)共被选择次,根据算子的得分,算子di(或者ri)的权重计算公式为

式中:μ为反应参数,表示上一次邻域搜索迭代的算子表现对其权重影响程度。根据每个算子的权重,通过轮盘赌的方法,选择下一次被选择的算子,每个算子di(或者ri)被选择的概率为

式中:OD为所有破坏算子的集合。
2.1 生成初始解
采用基于贪婪思想的插入算法生成1 个初始可行解。在初始解中,只考虑始发港为海港的航线,以确保找到的解总是可行的。将所有港口按照距离海港的航行距离降序排列,记为P′。首先构造1 条只有从海港发出并且返回海港的空载航线{0,0,0}。
令Δfig为将港口i插入航线g的最佳位置所带来的成本增加值,如果将港口i插入船舶路径g中不满足约束,则Δfig=∞。依次将港口i插入到当前解的航线池G( )S中,所获得的成本增量的最小值为。每次都从P′中选择1 个港口插入到当前航线池G(S)的最佳位置,保证满足载重量约束、航次长度约束和服务时长约束。
当未被访问的港口P′均因为服务时长约束(所有内外贸集装箱运输必须在1 个规划周期内完成)无法插入到现有航线的任何位置时,可以考虑构造1 个新的航线,该航线不再从海港发船,而是从1 个枢纽港发船。构造初始解的具体过程如算法1所示。

算法1 构造初始解S输入:港口集合P;P′←将P 按照距离海港的距离降序排列,G( )S ←∅;While P′≠∅do i ←从P′中取出第一个港口;If ∃Δfig<∞,g ∈G( )S then插入i 到航线arg min g ∈G( )S { }Δfig 的最佳插入位置;Else从距离i 最近的枢纽港出发访问港口i;End if P′←P′{}i,更新G( )S;End while输出:初始可行解S。
2.2 破坏算子设计
在本文中,破坏算子从当前解的构成航线中取出一定数量的中间港口和始发港口。在某次迭代中,移除的中间港口数量在中产生一个随机数qI,其中,ρI为移除中间港口数量的上限。同理,移除的始发港口数量在中产生一个随机数qS。本文设计了5 种破坏算子,。
(1)基于服务完成时间近似度的中间港口破坏算子(d1)
在Shaw 提出的基于近似度算子的基础上,本文根据装载量和服务完成时间,构成中间港口的近似度越小,表示两个港口的近似度越大。
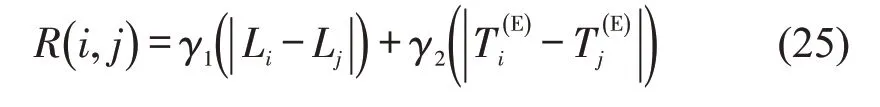
式中:γ1和γ2分别为装载量和服务完成时间在近似度中的权重;Li为当前解中,穿梭巴士到达i港口时船上的总装载量;为当前解中,i港口的外贸进口和内贸卸货集装箱到达i港口的时间,或者i港口的外贸出口和内贸装载集装箱到达海港的时间。
基于上述对两个中间港口近似度的定义,假设当前解为S,需要移除的中间港口数量为qI,移除的中间港口集合为R(I),则移除算子的步骤如算法2所示。
(2)基于移除成本最高的中间港口破坏算子(d2)
当把港口i从当前解S中移除后,模型的目标函数会有所下降。使目标函数下降最小的港口被认为是当前解S中“最差”的中间港口。破坏算子d2试图将其移除,并用修复算子将其重新插入到1个更好的航线中。令为从解S中移除港口i后对应的目标函数值。港口i从解S移除的成本为
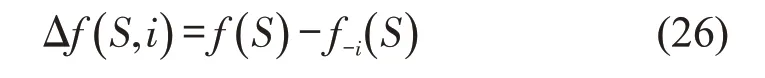
在该算子中,对当前解S中所有中间港口按照的升序排列,将移除成本最小的港口移除。移除港口i∗后,根据剩余港口的解结构,重新计算剩余港口的移除成本并按照Δf( )S,i的升序排序。不断重复此过程,直到共移除qI个中间港口。

算法2 基于服务完成时间近似度的中间港口移除算子d1输入:当前解S,需要移除的中间港口数量qI;在当前解S 中随机移除一个中间港口i,R( )I ←{}i;While ||R( )I (3)中间港口随机破坏算子(d3) 从当前解S中随机选择qI个中间港口并移除,设置该算子的目的是增加ALNS搜索的多样性。 (4)基于灵活时间的始发港口随机破坏算子(d4) 注意到,在该模型中每条航线是否可行取决于载重量约束、航线长度约束和服务时长约束。当1条航线上移除其始发港口并选择1 个新的始发港口出发,该航线的载重量约束始终满足。为提高新航线满足航线长度约束和服务时长约束的概率,本文引入灵活时间τg为w航线g中所有富裕航次时间(最大航次时间与某航次完成时间的差值)与航线富裕时间(周期长度与到达最后1 个港口时间的差值)。在该算子中,对当前解S中所有航线的灵活时间进行降序排序,依序选择前qS个航线,并移除选择航线上的始发港口。 (5)始发港口随机破坏算子(d5) 与破坏算子d3类似,从当前解S中随机选择qS个航线,并移除这些航线上的始发港口。 破坏算子是在当前解S中移除了qI个中间港口和qS个始发港口,修复算子旨在将这些中间或者始发港口重新插入到已修改的解结构中,产生新的或者更优的解。本文设计了2 种修复算子,。 (1)基于目标函数增加值的贪婪修复算子(r1) 该算子目的在于将移除的中间港R(I)按照一定顺序重新插入到它们的最佳位置。在本文中,每个中间港的插入顺序是根据插入前、后目标函数的增加值来计算。当前解S经过破坏算子移除操作后为S-,令表示在解S-的第l条航线的第k个位置插入港口i的目标函数。修复算子r1首先计算出每个中间港口i的最佳插入位置的目标函数,选择在最佳插入位置使目标函数增加最小的港口执行插入操作,再计算更新后的。重复以上过程,直到所有港口被重新插入到S-中。 插入一个中间港,该航线的载重量约束可通过在相应航次中加入插入中间港的装箱或者卸箱量来检验。转运约束可通过干线航次的当前运力是否能满足转运需求来检验。 (2)基于服务完成时间的贪婪修复算子(r2) 与基于目标函数增加值的贪婪修复算子类似,该算子同样是通过一定顺序将qS个被移除始发港的航线重新指定始发港。每个重新指定的始发港的表现则是通过整条航线的最早服务完成时间来衡量。寻找最早服务完成时间航线的优势是可以提高生成可行解的概率。注意到,为满足枢纽港与喂给港之间的从属关系(式(13)),若原本是支线航次,在重新指派始发港时,可指派原来的枢纽港或直接从海港出发。 为使自适应大邻域搜索算法能够搜索更大范围的邻域,增加跳出当前局部最优解的概率,本文利用模拟退火相关接受新解的规则进行设定。假设当前模拟退火温度为T,则可以根据如下准则判断是否接受新解S′:如果f(S′) 本文以上海港为枢纽海港,以上海和长江干线港口泸州、重庆、武汉、安庆、宜昌、黄石、九江、太仓、铜陵、南京、扬州、镇江、泰州、常州、江阴、张家港、南通、常熟、荆州等19 个港口间的内贸集装箱运输和外贸集装箱运输为(1 家航运企业)实例,分析内外贸同船政策对长江经济带穿梭巴士网络影响。本文选取重庆、武汉、南京和太仓作为枢纽港,假设其他港口只能喂给1 个枢纽港。枢纽港及其喂给港如图3所示。 图3 枢纽港及其喂给港Fig.3 Hub ports and feeder ports 泸州是重庆的喂给港,宜昌、荆州、黄石和九江是武汉的喂给港,安庆、铜陵、扬州和镇江是南京的喂给港,泰州、常州、江阴、张家港、南通、常熟是太仓的喂给港。本文规划周期为1周,受南京长江大桥和水深影响,假设穿梭巴士采用统一船型[11],即300 TEU,航速22 km·h-1,燃油成本550 元·h-1,固定运营成本21000 元·周-1。根据现有航线,最大航次长度为5100 km(包含下游到上游和上游到下游2个过程),转运成本为500 元·TEU-1。 内外贸同船运输重塑了长江经济带穿梭巴士的网络结构,实施该政策后,总运输成本下降23.6%,节约穿梭巴士13艘。当内外贸集装箱不能同船运输时,穿梭巴士的直达航次比例较低,为了提高舱位利用率,需要挂靠更多的港口,因而,穿梭巴士周转时间增加,需要投入更多的穿梭巴士以保证每个港口的服务频率。当内贸集装箱和外贸集装箱可以由同一船舶运输时,穿梭巴士不用经过太多港口就可以达到87%的舱位利用率,内贸集装箱和外贸集装箱相互补充,可以开通更多的直达航线,加快集装箱的流转。内外贸同船运输政策下,平均舱位利用率可达87%,穿梭巴士一周平均运营时长为149 h。 表2 内外贸不同船运输和内外贸同船运输的结果比较Table 2 Result comparisons of two transport policies 图4 长江经济带穿梭巴士网络Fig.4 Shipping Network Design in Yangtze River Economic Belt 长江上游至下游方向喂给港集装箱运输方式如图5所示。长江上游泸州港的内外贸集装箱运输量较少,52%需要在重庆转运,与重庆的运输需求进行整合,由重庆始发航线运往上海,剩余48%经泸州-重庆-上海航线运达上海。长江中游宜昌港、荆州港的内外贸集装箱运到武汉,经武汉中转,运达上海。而九江港的内外贸集装箱运输量相对较多,大部分通过黄石-九江-上海航线满足运输需求。长江下游设有南京、太仓两个枢纽港,除了江阴、铜陵、南通的内外贸集装箱运输需求较少外,其他港口的运输需求较大。在内外贸同船运输政策的作用下,经枢纽港直达上海的内外贸集装箱占66%,加密了太仓港到上海的直达航线。同时,长江上游、中游、下游枢纽港间的航线也有所增加。 图5 长江上游至下游方向喂给港集装箱运输方式Fig.5 Transport mode from upstream to downstream 长江经济带下游港口内外贸集装箱运输需求远大于上游和中游。本文主要针对下游枢纽港数量进行敏感性分析,研究枢纽港数量对穿梭巴士网络的影响,共设置4 种情境。情境1,只设置南京港;情境2,只设置太仓港;情境3,同时设置南京港和太仓港;情境4,同时设置南京港、南通港和太仓港。 本文通过EHHI指数衡量枢纽港数量对下游港口系统集装箱集中度的影响。 式中:n为下游港口数量;Ei为港口i的吞吐量。 当仅考虑南京港作为枢纽港时,长江下游港口EHHI值要低于仅考虑太仓港作为枢纽港时的EHHI值,如图6所示。 图6 不同枢纽港下长江下游港口EHHI 和穿梭巴士总成本Fig.6 EHHI and total costs with different hub port settings in downstream 长江下游仅考虑1个枢纽港时,穿梭巴士总成本增加了6%~17%。相对于南京港,太仓港距上海较近,具有区位优势,南京港与太仓港共同作为枢纽更有利于为中上游内外贸集装箱提供中转、集并和分拨服务,降低总运输成本。当考虑南京、南通、太仓共同作为枢纽港时,EHHI值和穿梭巴士总成本均有所下降,南通港位于南京港和太仓港之间,可承接长江中上游货物的中转,同时也有一定的挂靠南京和太仓间下游港口的区位优势。但是,新增加南通港后,84%的长江中上游内外贸集装箱仍通过南京港和太仓港进行中转。 本文对设计自适应大邻域搜索算法性能进行了分析,如表3所示。 表3 大邻域搜索算法性能Table 3 Performance of Adaptive Large Neighborhood Search 当港口规模为5时,自适应大邻域搜索算法和Cplex 获得的解相同,但自适应大邻域搜索算法的计算时间小于Cplex的计算时间。当港口规模超过5时,Cplex无法在3600 s内获得最优解。随着港口规模的增加,自适应大邻域搜索算法的计算时间虽然增加了,但是,均可获得优于Cplex 的解,算法的求解效率较好。 本文得到的主要结论如下: (1)提出内外贸同船运输政策下长江经济带穿梭巴士网络的优化模型。通过实例分析可得,内、外贸同船运输政策的实施有利于优化长江经济带穿梭巴士的网络结构,该政策实施后,内外贸集装箱运输需求相互补充,不再割裂,穿梭巴士航线可以减少挂靠港口,增加由枢纽港至上海港的航线密度,加快穿梭巴士的周转,直达航次比例由原来的15%增加到32%。另外,内、外贸同船运输政策为航运公司带来了经济效益和社会效益。政策实施后,节约23.6%总成本,平均舱位利用率可提升至87%,在保持服务频率和水平不变的情况下,降低了穿梭巴士的投入和穿梭巴士网络的碳排放。 (2)枢纽港的选择对长江经济带穿梭巴士网络的运营效率尤为重要。对于长江经济带下游,将南京港和太仓港同时作为枢纽港更有利于为中上游内外贸集装箱提供中转、集并和分拨服务。相比于设置1 个枢纽港,穿梭巴士总成本可节约6%~17%。在国内、国外双循环的背景下,长江经济带将承担更多的内外贸集装箱运输。这种情况下,航运企业可以考虑增加南通港作为枢纽港,分担部分南京港和太仓港的中转需求。2.3 修复算子设计
2.4 新解接受标准设定
3 实例分析
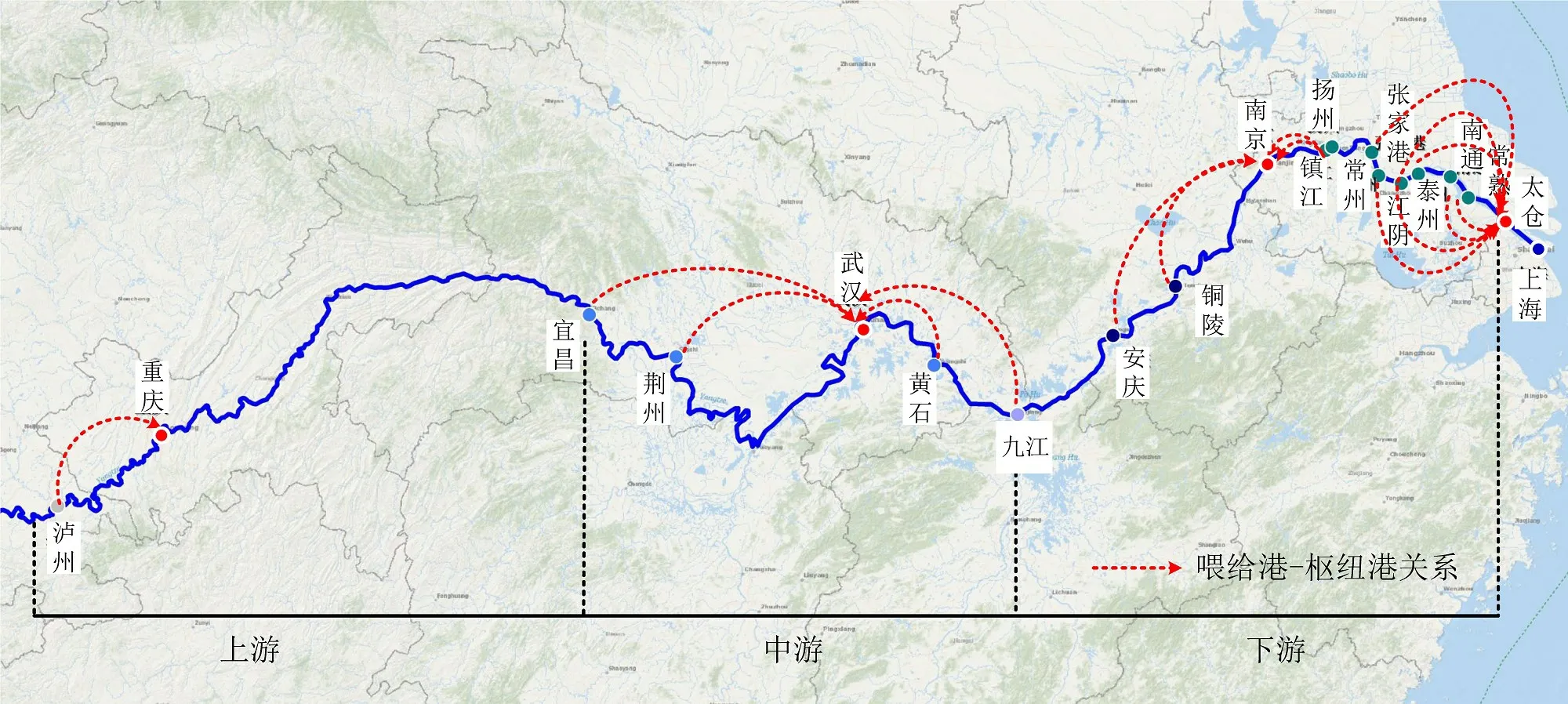
3.1 内外贸同船运输政策的影响分析


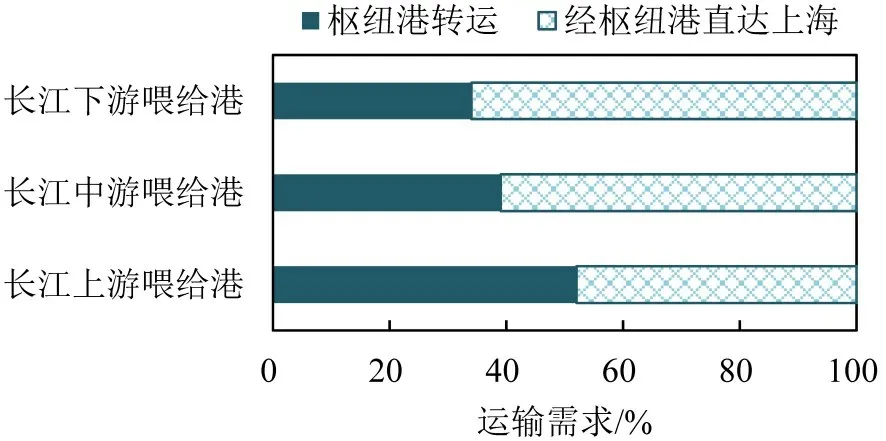
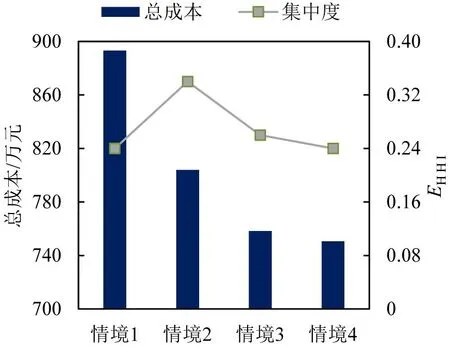
3.2 针对枢纽港数量的敏感性分析

3.3 算法性能

4 结论

