基于综合效用函数和动态策略空间的发电商竞价模拟方法

李洪波， 郭琦， 袁少卿， 吕小凡， 赵静

(1.内蒙古电网电力调度控制中心，内蒙古 呼和浩特 010020；2.北京清能互联科技公司，北京 100080)

0 引 言

电力市场的建设和运营是一项极为复杂的任务工程，为了降低市场运营给系统带来的风险，规避隐藏的试错成本，电力市场模拟系统的建设显得尤为重要。对此国内外工作者已经研发了多种电力市场模拟系统[1-5]，然而其主要集中在市场运营商的出清环节，对市场成员的竞价决策行为往往作了简化处理。随着电力市场的不断发展，如何有效模拟市场成员的竞价行为逐渐成为各学者关注的重要课题之一。

基于代理的模拟仿真技术是一种有效的试验工具[6-8]，可为上述问题提供可行的解决思路。文献[9]针对电力拍卖市场，提出了一种基于选择概率的强化学习算法的智能代理模型。文献[10]提出了基于猜测供给函数模型的发电公司代理模型，并构造了重复博弈电力市场的多代理模型。文献[11-13]基于Q学习算法构造了发电商决策代理模型，并分别在现货和中长期市场验证了模型的有效性。文献[14]72-73提炼出关键影响因子用于建立多输入决策因子模型，并应用RE-learning算法模拟发电商日前市场竞价行为。

综上所述，目前国内外基于智能代理的发电商竞价模拟研究已经取得了一定成果，但多集中于单一决策目标，缺少多重决策目标的分析建模，此外在代理进化学习过程中，策略空间一般是固定的，这在一定程度上限制了代理模型的灵活性。针对上述问题，本文提出一种基于综合效用函数和动态策略空间的智能代理方法，同时结合强化学习中的RE-learning算法，实现对市场成员竞价行为的模拟，并通过算例验证所提方法的有效性。

1 综合效用函数和动态策略空间

1.1 综合效用函数

理想情况下，发电商进行第二天申报时，往往追求的是个人收益的最大化。然而实际中，由于生产经营条件的不同，发电商追求的可能不仅仅是单一收益，还会考虑其他从属目标，如机组相对利用率和机组市场占有率等。此外，在衡量各策略的优劣性时，各发电商关注的可能不是整体收益，而是机组容量收益。因此，为了有效模拟发电商的上述真实行为，本文借鉴文献[14]73-75中的方法，综合考虑机组单容量收益和相对利用率等因素，构造一个综合的效用函数，具体如式(1)所示。

(1)

(2)

(3)

式中:plmp为机组所在节点的市场出清价格；Q为机组中标电量；C(Q)为机组的变动成本；CGu为固定成本分摊后的竞价成本；G为机组装机容量；Gω为市场总装机容量；Beq为系统负荷。

1.2 动态策略空间

基于强化学习的智能代理研究中，策略空间的构建是关键所在。在现有的研究中，通常采取简化处理，首先对机组的容量范围进行分段均分处理，并固定形成量的基准申报方式；其次基于边际成本函数，结合容量申报方式，从而得到一条基准的申报曲线即基准策略；最后基于上述基准策略，等比例考虑一定的利润率，从而形成对应的策略空间。显然，上述处理方式存在着不少问题:第一，各策略中量都是采取固定统一的分段均分方式，这显然无法模拟发电商的真实行为，也无法从量上体现各策略的优劣性和发电商在申报量上的博弈行为；第二，在进化学习过程中，各代理策略空间都是固定的，这在一定程度上限制了代理模型的灵活性，也难以体现其学习性和智能性。

实际中，为了实现自身决策目标最大化，在市场允许范围内，各发电商一般都会报满N(申报段数)个量价对即申报策略曲线。对此，为了模拟发电商在量价维度上的真实考虑和博弈行为，本文对各策略的优化空间进行了维度还原处理，各策略对应的优化维度不再是单一的利润率拉升比例，而是真实的N个量价对。

此外，针对上述所提的第二点不足，本文提出一种改进的动态策略空间。在每轮次学习过程中，对各策略评价系数重新进行排序，排序靠后的策略将会进行动态调整替换，其中替换更新思路主要有以下两种方式：第一，向本轮次最优策略进行动态学习；第二，基于本轮次最优策略随机扰动生成新策略。

1.3 竞价模型

各发电商向市场运营商提交申报信息，运营商根据购电成本最小或者社会福利最大化原则统一进行市场出清。每天电力市场的重复运营，使发电商根据当天的竞价经验不断动态优化后续的竞价策略成为可能。

策略进化过程如下：①各发电商提交报价信息给市场运营商；②市场运营商收到所有的报价信息后，在满足系统负荷需求等条件下，根据市场规则进行出清，即制订发电计划、计算电网各节点价格及各发电商的中标电量，并将这些出清结果反馈给各发电商；③各发电商根据反馈的出清信息，更新计算本轮交易的综合效用函数值；④各发电商根据综合效用函数值和竞价经验优化竞价策略，进行第二天即下一轮的报价。

2 智能代理求解算法

图1 算法流程图

本文采用强化学习中的RE-learning算法搭建各发电商的竞价模型，该算法首次由Roth和Erev在1995年提出，算法原理和相应的决策模块见文献[11]。此处以发电商i为例详细介绍该算法的具体求解过程，对应流程如图1所示。

所提方法中各策略包含了2N个优化变量，即对应N个量价对，其中N个变量为申报容量，另N个为对应的申报价格。对于各优化变量，其初始化方式具体如下：

Ck,j=Cj,min+rand×

(Cj,max-Cj,min)

(4)

式中:k、j分别为动作和变量下标，j∈2N;Cj,max、Cj,min分别为变量Cj的上下限值。基于随机初始化的量价变量，为了保持申报曲线中各段量价非单调递减特性，对量价变量分别重新进行排序处理。

以竞价模型的单次策略进化过程为一轮次，则第D轮市场出清后，根据反馈的市场出清结果计算式(1)的综合效用函数值，并利用其更新策略空间中各策略动作的学习参数，式(5)是对选择到的第m个动作进行更新，式(6)是对未选择到的动作进行更新。

(5)

(6)

根据D轮出清结果更新完原始策略空间的评价系数后，按照所提的改进思路动态调整更新策略空间，具体操作为：根据更新后的评价系数对各策略重新进行优先级排序，假设评价系数最高的动作k下标为b，排序最后m个动作下标集合为M，排序最后m～m+n个动作下标集合为N；对动作集合M采取向最佳策略n学习的改进策略，对动作集合N采取最佳策略b随机扰动替换策略，其策略变量及评价系数的更新方式具体如下：

(7)

(8)

式中:Cm′,j、qim′(D+1)分别为动态替换后的第m个策略动作及对应的评价系数；biasj、biasq分别为变量j和评价系数的扰动量；rand为(0,1)的随机量。

根据动态调整后各策略行为的评价系数更新其在轮盘赌中的概率系数，更新公式如式(9)所示。下一轮竞价时，重新以轮盘赌的方式随机选择对应的策略动作。

(9)

式中:c(D+1)为D+1轮冷却系数，决定评价系数对选择概率的影响程度。参数的选择根据每轮各策略评价系数进行如下调整：

(10)

式中:g为一个大于0的实数，一般设定的取值范围为(0,3)。g的取值会改变冷却系数c的取值，影响智能代理的收敛效率，g越大，智能代理收敛越慢。

3 仿真算例

3.1 场景设置

图2 3机9节点系统接线图

为了验证所提方法的有效性，以3机9节点系统为例，其网络拓扑如图2所示，可见其包含3个发电商、3台变压器、6条输电线路以及3个电力用户，各发电商的详细信息如表1所示，节点用户负荷和线路传输容量信息可详见表2和表3。

为了便于处理，仿真中假设各发电商代理模型采取相同的参数设置，策略动作总个数K=21、遗忘因子r=0.09、经验参数e=0.9、集合M和集合N个数均为2。

此外，仿真中以广东现货电力市场试结算规则为例，采取统一节点电价出清机制；各发电商最多可上报5个量价对，同时报价策略在全天24 h各时刻是统一的，不得中途变更。仿真中还要求各段价格须单调非递减，各段容量需要≥0，且各段容量之和不得超过机组最大出力。

表1 发电商技术经济参数

表2 节点负荷信息

表3 变压器及线路信息

3.2 仿真分析

3.2.1 算例1

本算例中为了验证所提动态策略空间的改进效果，发电商1～3均采用智能代理模型，但代理模型的决策从属目标仍设为单一的全天总收益。改进前后动态竞演过程分别如图3～图4所示，为了进一步对比效果，此处对市场均衡后各发电商代理的决策从属目标值作了统计，如表4所示。

由图3～图4及表4的仿真结果可以看出，所提的动态策略空间，会对市场均衡收敛速度有所影响。相比改进前有所变慢，但各发电商从属决策目标值有所提高，相比改进前市场能探索到一个更优的收敛点。这主要是由于动态策略空间中，对各策略优

图3 改进前动态竞演过程

图4 改进后动态竞演过程

表4 市场稳定后收益统计对比

化变量进行还原处理，因此各代理策略空间范围变大了。此外在迭代竞演过程中，对原始策略空间进行动态调整优化，这一定程度上也影响了整体的收敛速度，但同时得益于动态策略空间的改进优化，市场稳定后各发电商整体达到了一个更优的均衡状态。

3.2.2 算例2

本算例主要是为了模拟发电商决策从属目标由单一的全天收益，变为综合效用函数后，其动态竞演的变化过程。因此在本算例中，假定发电商2和3均按300元/MW满容量申报，而发电商1采取所提的改进代理模型，同时综合效用函数中机组相对利用率权重比例设为2，仿真结果如图5、图6和表5所示。

由图5～图6及表5的仿真结果可以看出，当发电商1采取综合效用函数后，其全天总收益将有所减小，总中标电量有所增加。这主要是由于改进后发电商决策目标不再是简单的收益最大化，而是收益和中标电量的综合效用值。

图5 全天总收益对比

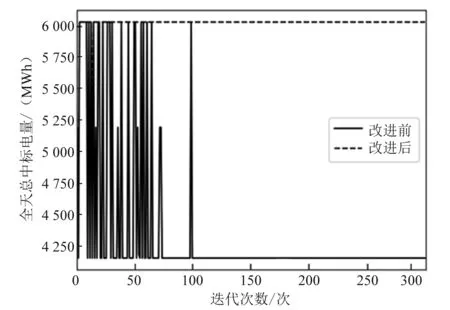
图6 全天总中标电量对比

表5 市场稳定后决策从属目标统计对比

4 结束语

为了有效模拟实际电力市场环境中各发电商的真实竞价行为，本文提出了一种基于综合效用函数和动态策略空间的竞价模拟方法。算例仿真结果表明，所提的动态策略空间稍有牺牲市场均衡的收敛速度，但能探索到一个更优的均衡点。此外，基于所提的综合效用函数，所提代理模型能一定程度上反映各发电商的实际竞价和对总体收益和机组相对利用率之间的综合考虑行为。