基于似然剖面分析的直驱风机变流器辨识建模方法
石天成, 汪可友, 舒德兀
(上海交通大学 电力传输与功率变换控制教育部重点实验室,上海 200240)
0 引 言
在风力发电机中,直驱风机具有低风速下效率高,噪音低,维护成本低等特点,因而得到了广泛的应用。直驱风力发电系统包含风力机、发电机及其控制系统、传动系统、变流器及其控制系统等模块。变流器为风电机组的核心组件,对风力发电系统的电能质量和维持稳定性具有重要作用。变流器的控制系统通常采用背靠背变流器,目前比较成熟的控制策略为基于矢量控制的串级双环控制。对于仿真而言,大型风电场的控制器参数往往不会给出,只提供风机外特性和性能指标,这对仿真研究带来了一定的困难。目前风电场建模方法通常采用等值和辨识来处理复杂的结构和未知的参数。
本文利用统计学中的似然剖面概念,提出一种针对变流器参数辨识的定量分析方法,结合差分进化辨识算法,不仅能够分析参数的可辨识性和结果的可信度,同时也可以对辨识数据的可用性进行评估,为变流器辨识建模提供指导。
1 直驱风电机组的数学模型
本文的研究对象为永磁直驱风力发电系统,其拓扑结构如图1所示。
当转子磁场恒定时,机侧电磁转矩与q轴电流成正比。机侧变流器的控制方程如式(1)所示。
(1)

(2)
式中:Kω、Tω分别为外环PI调节器比例和积分系数。
转速参考值ω*通常由桨距角控制给出。
网侧变流器的控制目标为维持变流器直流电压恒定,通常采用电网电压定向的方式,其控制方程为:
(3)


图1 直驱风力发电系统拓扑结构[1]

2 参数可辨识性与灵敏度分析
参数的可辨识性一般用来衡量模型中的一个参数在一定的激励和量测精度的条件下的准确辨识性。“参数可辨识”是指模型的参数有唯一解,且这个唯一解可以通过一定的算法来得到;“参数不可辨识”是指模型的参数无解或者有多个解。对于直驱风机系统,大多数模块都是非线性模型,因此很难一分为二地判断某个参数是可辨识的或者不可辨识的。因此需要定义一个辨识性指标,来准确地衡量参数的辨识难度,从而对模型设计和辨识参数的选择提供指导意义。
变流器控制模型参数的可辨识度可以利用灵敏度分析的方法来进行。常用的灵敏度分析方法为轨迹灵敏度分析[2]。在优化辨识的过程中,当一个参数变动时,其他参数并不会保持原数值不变,而是在辨识算法的作用下进行调整。因此,轨迹灵敏度的分析方法针对辨识算法未必是最为准确的。因而本文采用基于统计学概念的似然剖面法[3]进行灵敏度分析。这种方法与灵敏度分析的核心区别就在于计算灵敏度时优化其他参数以使得目标函数最小,从而使可辨识性分析的过程更加接近实际优化辨识的过程,也可以表现出不同的辨识数据对参数可辨识性的影响。
2.1 参数辨识原理
参数辨识本质上是一个优化拟合问题,即找到一组参数,使得待辨识模型的输出能够与给定输出数据尽可能吻合。
非线性系统的状态方程可以描述如下:

(4)
式中:x(t)为状态变量;y(t)为输出;u(t)为输入;p为模型结构参数;e(t)为量测噪声;θ为需要辨识的参数集合。
目标函数通常采用最小二乘误差来定义:
(5)
式中:W(θ)为目标函数值;yi为第i维输出的输出值;ypi为模型结构为p时的辨识输出值;σi为第i维输出的标准差,用以对数据进行归一化。
2.2 似然剖面法灵敏度分析原理
当测量误差满足正态分布时,加权最小二乘估计和极大似然估计的目标函数满足以下关系:
V(θ)=-2log[L(θ)]+const
(6)
式中:V(θ)为最小二乘目标函数;L(θ)为极大似然目标函数;θ为待辨识参数向量。
定义参数的似然剖面函数:
(7)

(8)
因此,在θi的显著性水平为α时,其最小二乘目标函数满足卡方分布:
(9)
式中:df为自由度,其值可取1。
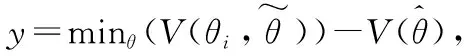
2.3 参数辨识算法
差分进化(differential evolution, DE)是一种基于群体差异的启发式随机搜索算法,它的特点是收敛迅速、鲁棒性强,且对初值依赖程度低。变流器参数众多,初值的选取是难以确定的,因此选取该算法作为辨识算法。
具体辨识流程如图2所示。

图2 差分进化法辨识流程图
3 永磁直驱风电场变流器参数辨识
采用如图3所示的仿真系统进行灵敏度分析验证,其永磁同步电机与控制器拓扑与上文描述一致。于35 kV出口处设置三相接地短路故障实现电压暂降,采集机侧、网侧变流器出口点的端电压和电流作为输入数据进行仿真分析。

图3 仿真系统示意图
3.1 辨识模型与灵敏度分析
风机出口处的d、q轴电压电流和线路及变压器等值阻抗视为已知。依据公式及变压器的变比,可以计算出变流器出口处的d、q轴电压和电流。根据网侧变流器的控制方程,选取观测量为:
(10)
由于本文使用的仿真模型中,网侧变流器d、q轴控制参数相同,因此只考虑扰动中变化较为明显的d轴控制环节进行辨识。
依据网侧和机侧变流器控制方程,按照梯形法对微分方程进行差分化,得到待辨识参数相关的差分方程为:
(11)

根据式(1)、式(2),得到机侧变流器的差分方程为:
(12)
网侧变流器和机侧变流器分别辨识,其辨识的目标函数都设置为观测目标y序列的测量值与估计值的最小二乘误差,即:
(13)
设置三相短路故障的短路位置,使得风机出口处电压降落分别为90%和50%, 对机侧变流器和网侧变流器参数进行辨识灵敏度分析,分析结果如表1~表4所示。同时,测试单相故障的辨识效果如表5所示。

表1 GSC参数灵敏度(90%压降)

表2 MSC参数灵敏度(90%压降)

表3 GSC参数灵敏度(50%压降)
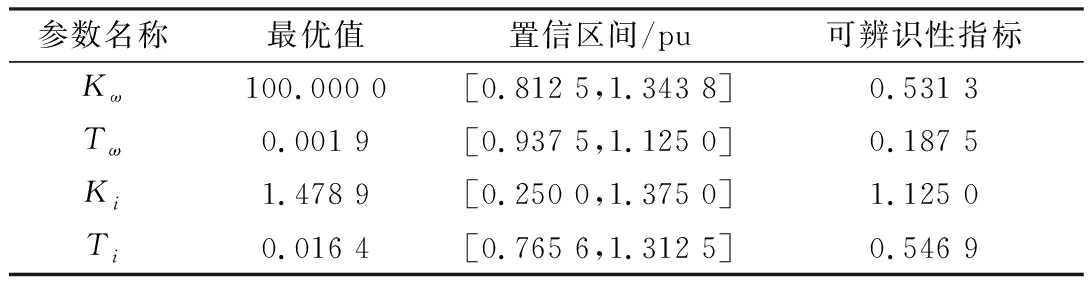
表4 MSC参数灵敏度(50%压降)

表5 GSC参数灵敏度(单相90%压降)
由表1~表4可以看出,在严重三相故障中,网侧变流器参数的可辨识性指标更小,因此网侧参数更易辨识。而故障较轻时,网侧变流器辨识困难,而机侧变流器仍具有可信辨识效果。在同一变流器中,外环参数相较内环参数,更易于辨识。因此在测量误差较大,辨识结果不可信时,可以对辨识模型进行优化,以时延模块代替内环参数。由表1和表5的对比可以看出,单相故障虽然也可以辨识,但是辨识结果的可信度远不如三相故障。
3.2 辨识方案与辨识结果
依据上节的灵敏度分析结论,对图3所示的直驱风机系统中,在靠近风机出口位置设置三相金属性短路故障。直驱风机输出额定功率为1.8 MW,直流侧额定电压为1.5 kV。三相故障使得网侧变流器出口处压降为90%,故障时间为0.5 s,对测量电气量加入幅值0.05 pu,均值为0的随机误差。按照2.3小节所述步骤进行机侧和网侧变流器参数的辨识,得到辨识结果如表6~表7所示。

表6 MSC参数辨识结果

表7 GSC参数辨识结果
从表中可以看出,机侧变流器的辨识误差是略高于网侧变流器的,此结果与灵敏度分析的结论相同。
对辨识模型设置与原模型相同的故障进行仿真,重要电气量波形与原模型对比如图4所示。从图4可以看出,辨识模型的输出电气量与原模型具有较好的匹配性。为了验证辨识模型的泛化能力,在t=5.0 s至t=5.5 s加入风速阶跃,风机的输入风速由14 m/s 突变至16 m/s,同时故障设置为单相金属性故障。验证辨识模型的电气量输出如图5所示。可以看出,辨识模型仍然能够具备与原模型相近的输出。

图4 辨识模型输出结果
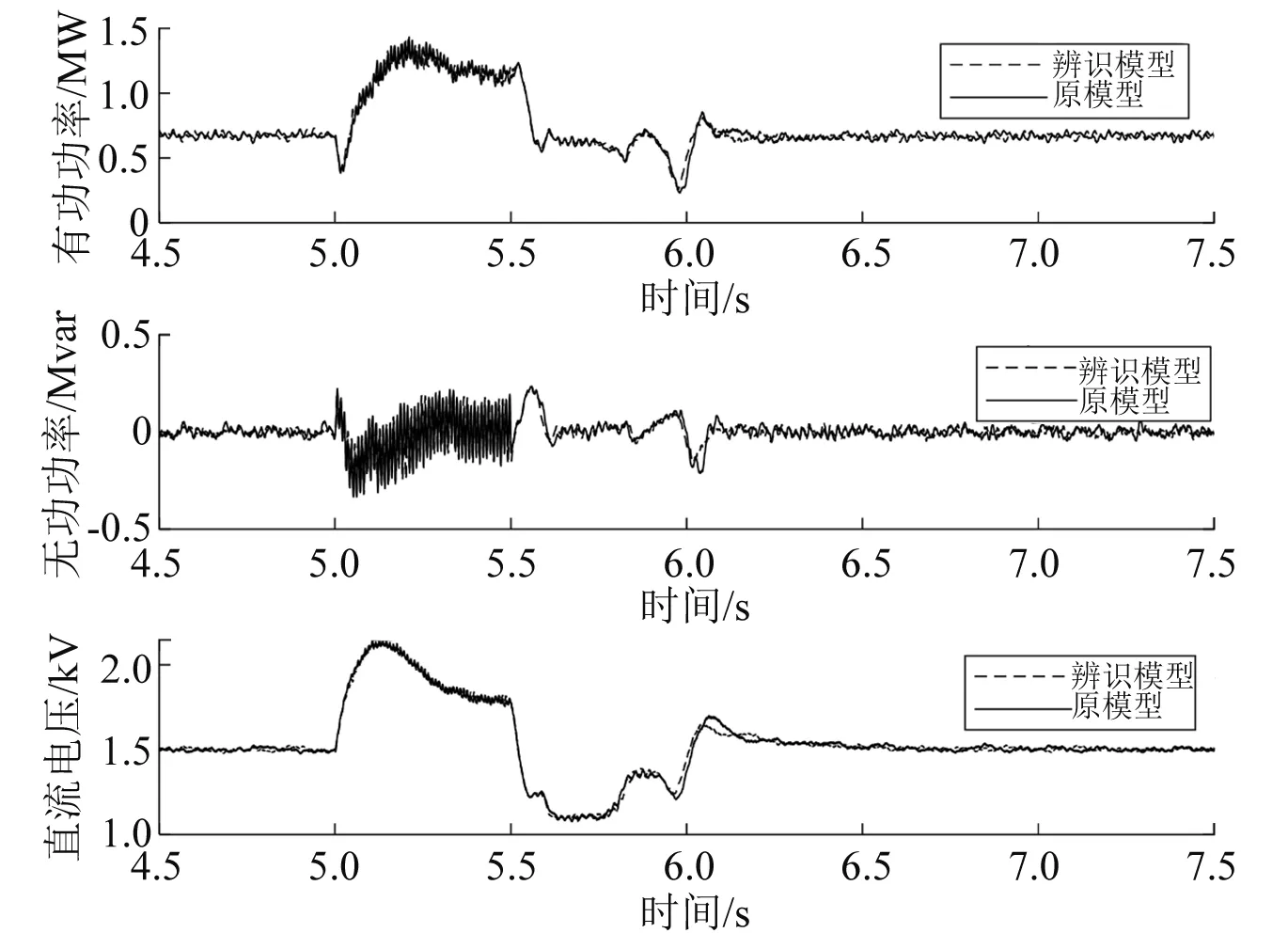
图5 风速阶跃扰动下辨识结果
4 结束语
本文提出了一种基于似然剖面灵敏度分析的直驱风力发电系统变流器辨识方案。相较于传统的灵敏度分析,似然剖面分析能够从模型和数据两个方面分析辨识的有效性,可以判断使用特定智能优化辨识算法时,何种扰动对辨识结果最为有利;同时也能量化模型参数的辨识灵敏度,可以根据灵敏度的特性选择是否对模型进行优化。在最后的仿真试验中,采用了对辨识有利的三相故障扰动波形段进行参数辨识,并在不同情况下分析了模型的泛化能力,证明了本文所提出的辨识方案的有效性。

