基于滑块自助法与长短时记忆网络的电力负荷区间预测研究

刘义艳， 于太珊

(长安大学 电子与控制工程学院，陕西 西安 710064)

0 引 言

智能电网是电力系统发展的必然趋势，在“十三五”规划纲要中明确指出: 加强智能电网建设，提高电网与发电侧、需求侧交互响应能力[1]。负荷预测技术通过已有历史负荷数据的分析处理，实现对未来负荷的准确预测，可以合理地控制电网内各设备的启停，增强网内设备响应能力。

负荷预测的方法有很多种，如小波分析法[2]、马尔可夫链[3]、支持向量回归(support vector regression, SVR)[4]、循环神经网络(recurrent neural network, RNN)[5]以及一些组合算法[6-7]。这些算法在负荷预测精度上表现不错，但仍有很大不足，基于历史负荷样本进行点预测，只能计算出一个值。

针对上述现象，本文以斯洛伐克东部某电厂真实数据为数据来源，通过Bootstrap(自助法)与长短时记忆(long short-term memory, LSTM)网络的组合预测方法对未来负荷进行区间预测，设计一种量化描述未来负荷不确定性的算法。

1 电力负荷的区间预测

1.1 区间预测模型构建

基于Bootstrap建立样本，可直接利用原始样本数据辅助观测信息来进行统计推断，无需假设总体分布或做任何限制。构建步骤如下：

(1) 获取电力负荷原始数据集，建立时间序列样本X={x1,x2,…,xn},nòN+。

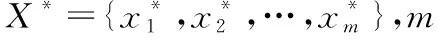
(3)对每个Bootstrap样本构建点预测模型。

(4) 预测值序列计算，通过上一个步骤中点预测模型分别对N个测试样本进行预测，获得包含M个预测值的序列。

(5) 利用区间估计法对M进行区间预测，即可得到电力负荷的区间[MIN，MAX]。

由于步骤(2)为随机抽样，但负荷数据具有时间连续性，随机抽样会破坏这种特性，由此引入滑块Bootstrap概念，将负荷数据按一定时间长度划分为块，形成新的时间序列样本，在此样本上进行上述步骤采样，获取Bootstrap样本。

1.2 预测模型评价指标

点预测模型评价指标：

(1) 平均绝对误差(mean absolute error, MAE)

(1)

(2) 均方根误差(root mean square error, RMSE)

(2)

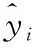
区间预测模型评价指标如下：

(1) 预测间隙覆盖率 (prediction interval coverage probability,

PICP)

(3)

式中:Lt和Ut为预测区间的上限和下限。PICP的值越大，说明落在预测区间的负荷值越多。

(2) 平均预测区间宽度 (mean prediction interval width,

MPIW)

(4)

式中:N为预测区间的个数。在保证PICP尽可能大的前提下MPIW的值越小越好。

(3) 综合指标(coverage width based criterion, CWC)

CWC=MPIW×[1+γ×e-η×(PICP-μ)]

(5)

2 数据处理及算法原理

2.1 数据预处理

数据点时间间隔为30 min。根据3σ准则，若负荷数据满足式(6)，则认为该数据为异常数据，将其填补为前后两个时间点的负荷平均值，计算公式如式(7)所示。

(6)

(7)

式中:σ为负荷数据方差；ε为阈值，通常取1～1.5。

为简化计算对负荷数据进行归一化，如式(8)所示。

(8)

2.2 LSTM预测模型

LSTM[8]是一种基于 RNN改进的网络，标准RNN结构如图1所示。

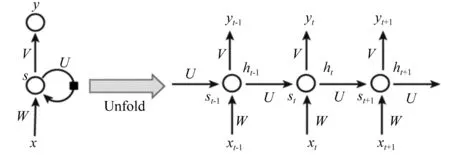
图1 RNN单元

图1中：xt为t时刻的输入；st为t时刻隐藏层的状态；yt为输出；W、U、V为参数。对于标准的RNN架构来说，由于门结构不变，伴随网络层数增多，会出现“梯度消亡问题”。

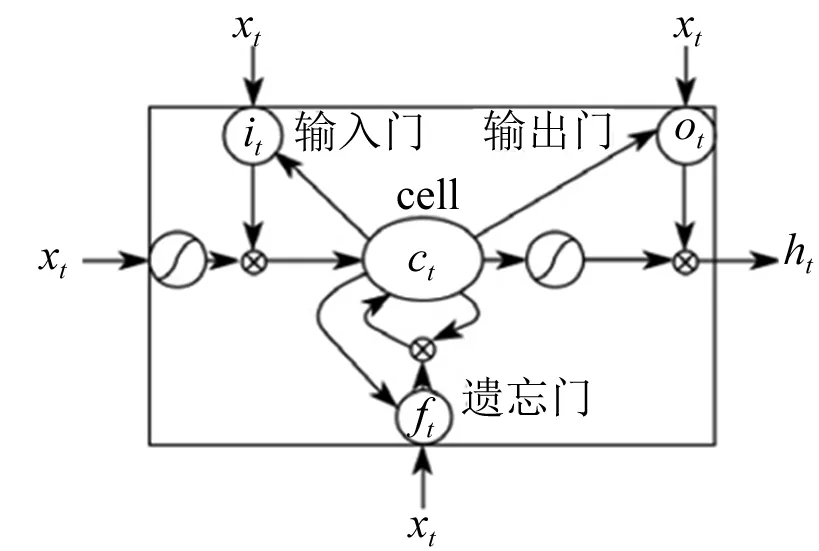
图2 LSTM单元

LSTM通过对RNN门结构的改善，对处理时间序列数据有很好的效果，结构如图2所示。

图2中，LSTM在每个RNN细胞元ct内加入了三个门控制单元，用来对关键节点的信息进行筛选操作。其中：xt为t时刻的输入；it为输入门用来控制当前时刻信息输入；ft为遗忘门用来选择当前细胞历史状态信息的保留；ot为输出门用来控制当前信息输出。按结构可表示为：

(9)

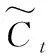
2.3 算法参数寻优

粒子群优化[9](particle swarm optimization,PSO)算法是一种群体智能的优化算法。PSO算法首先初始化空间中的一群粒子，每个粒子都代表极值优化中一个潜在的最优解，用位置、速度和适应度值三项指标表示该粒子特征。通过比较与极值点的适应度值更新粒子属性来推动粒子朝着个体最优值和群体最优值方向迭代直到全局最优解。

点预测模型与粒子群算法结合进行预测的流程如图3所示。

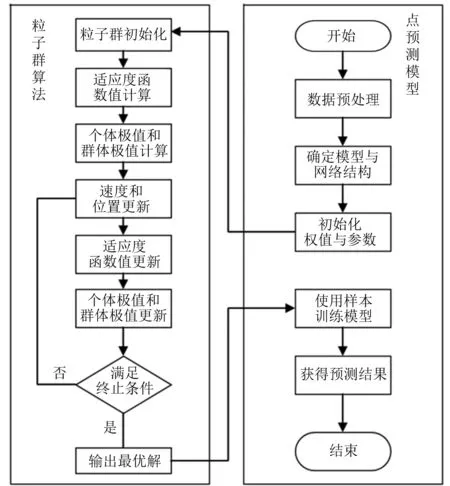
图3 模型预测流程

3 实例分析

本文以斯洛伐克东部某电厂一年内的真实负荷数据预测未来24 h内的负荷数据。数据划分为训练集85%，验证集15%。区间预测数据按1.1小节构造，抽样次数N=1 000。

3.1 确定点预测模型

针对不同算法模型中影响精度的超参数，采用PSO方法进行寻优。对LSTM模型，选取隐藏层第一层L1及第二层L2的神经元个数、学习率和迭代周期作为寻优特征参数。参数寻优结果如图4所示。故LSTM的特征参数选择为神经元L1=53个，L2=95个，学习率为0.04，迭代周期为42。

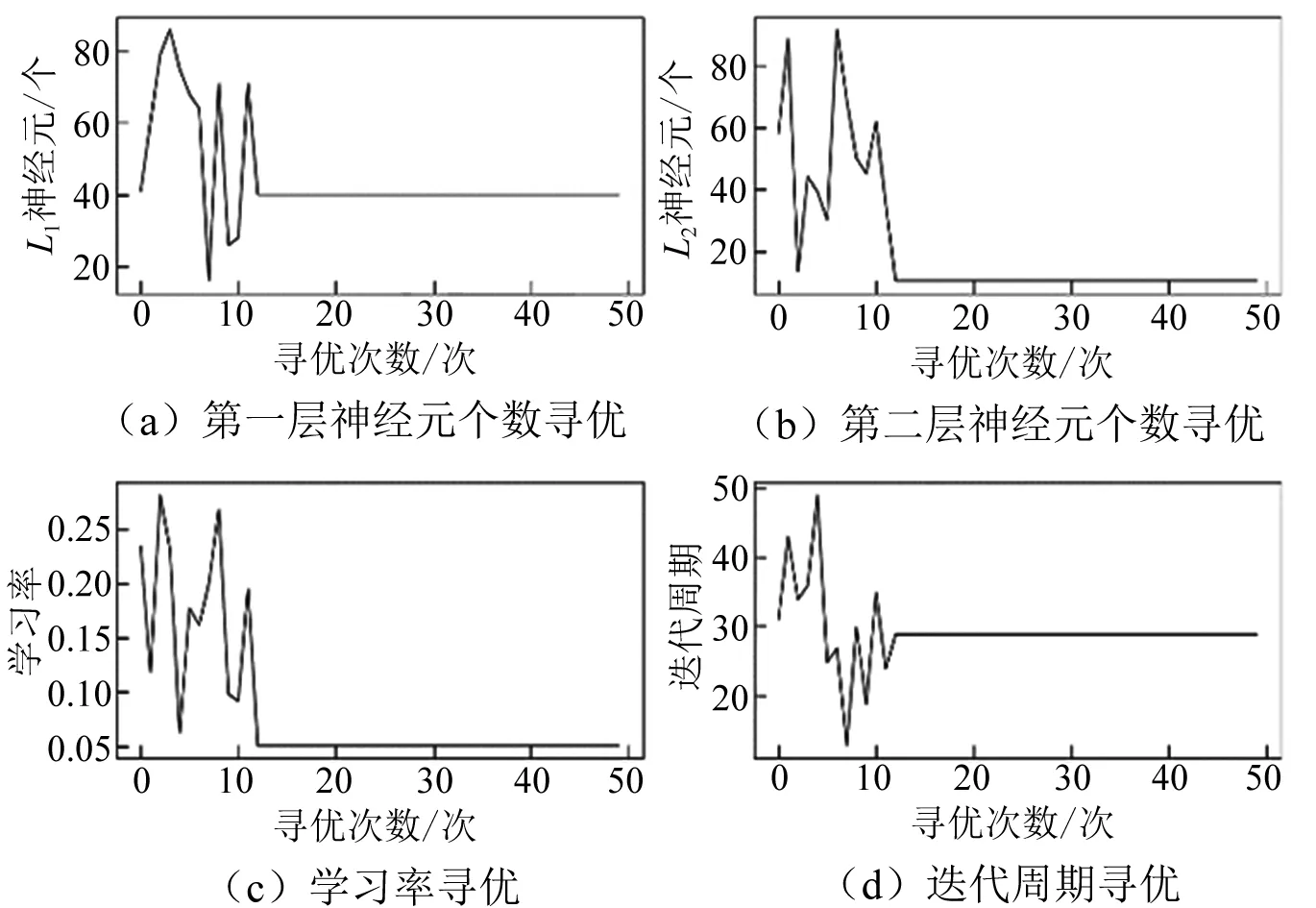
图4 LSTM参数粒子变化

在算法模型选取最优参数情况下，对不同预测算法模型输入相同的原始电力负荷数据进行预测，基于不同点预测模型的结果如图5所示。图6为图5的局部放大。

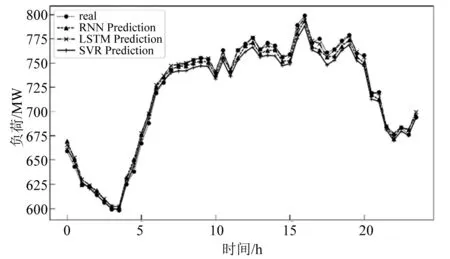
图5 SVR、RNN、LSTM点预测结果对比

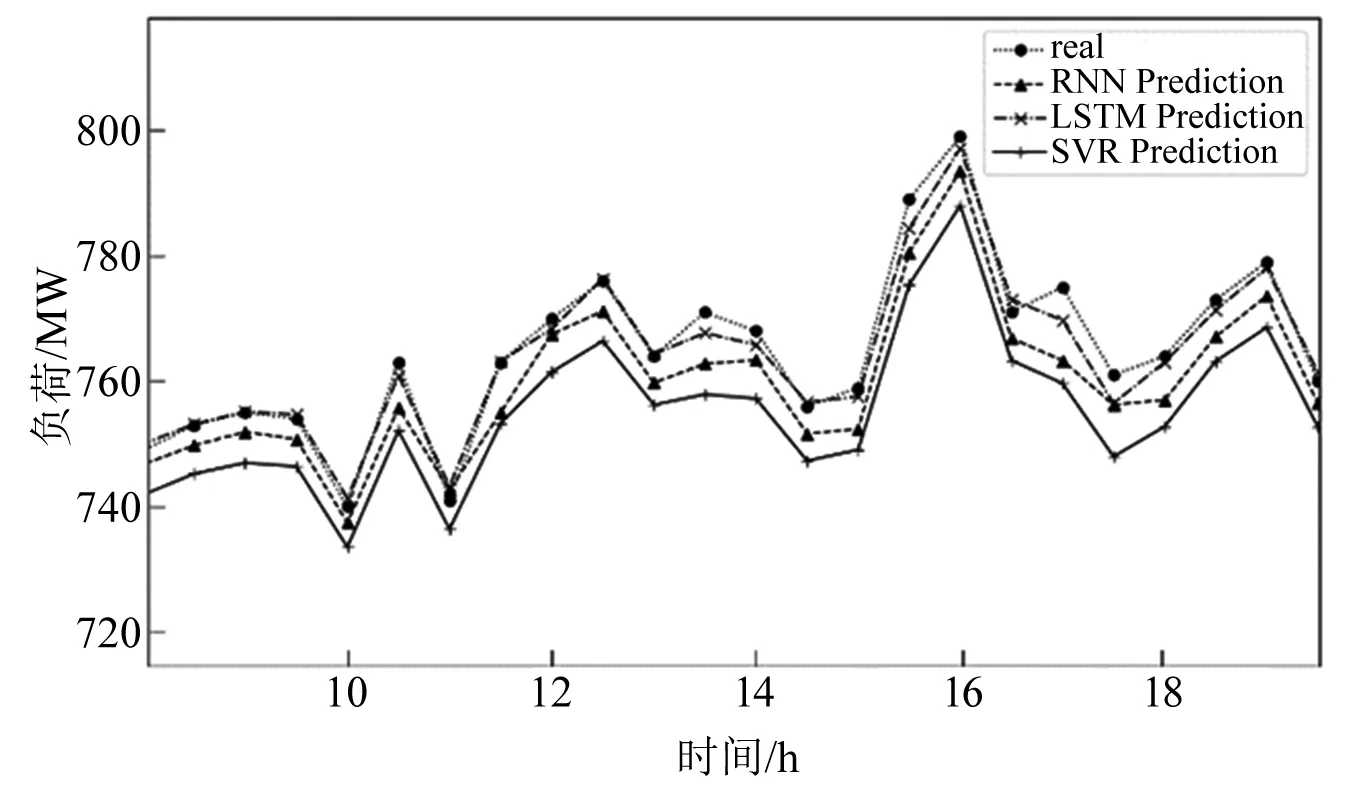
图6 点预测结果对比图局部放大

从图6可以看出，LSTM算法的预测结果更接近真实值。对比表1关于点模型的评价指标，MAE、RMSE，LSTM模型在预测精度具有显著优势，故选用LSTM作为点预测模型。

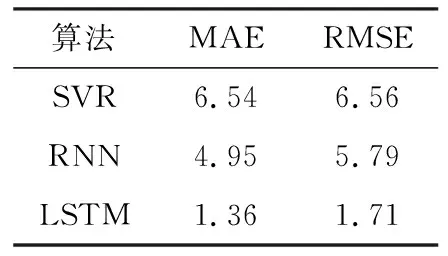
表1 误差对比

3.2 大子样区间预测

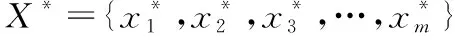
图7为LSTM模型不使用Bootstrap方法采样构造的预测值序列产生的区间估计结果，图8为图7的局部放大。图9为通过采用Bootstrap法采样获得预测值序列后产生的区间估计结果。图10为图9的局部放大，其预测结果如表2所示。

从图7～图10可以看出，B-LSTM法与LSTM法在MPIW相近条件下，PICP更高。由表2可知，B-LSTM组合的算法的置信区间CWC值明显小于单独使用LSTM算法。由此说明，基于LSTM与Bootstrap组合构建的预测区间为最优。

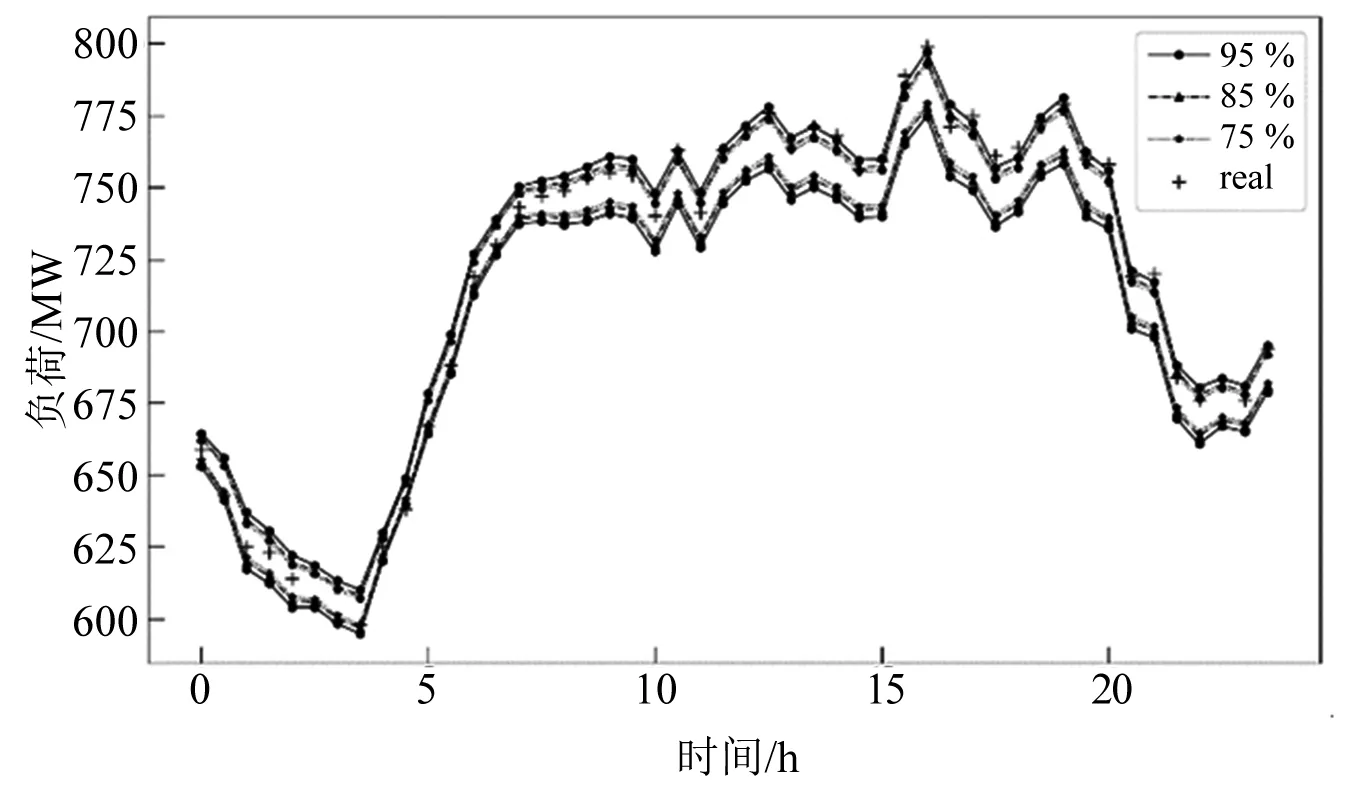
图7 LSTM区间预测结果

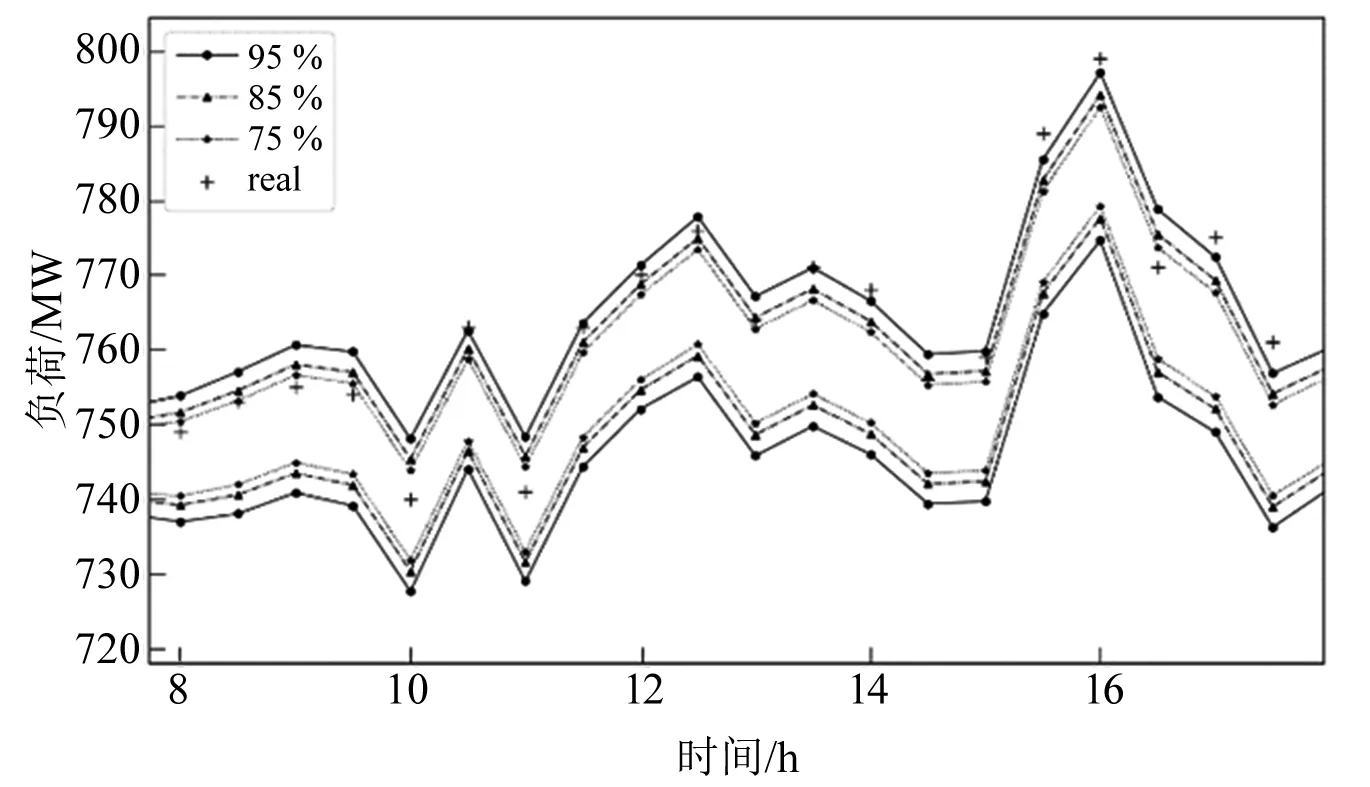
图8 LSTM区间预测结果局部放大

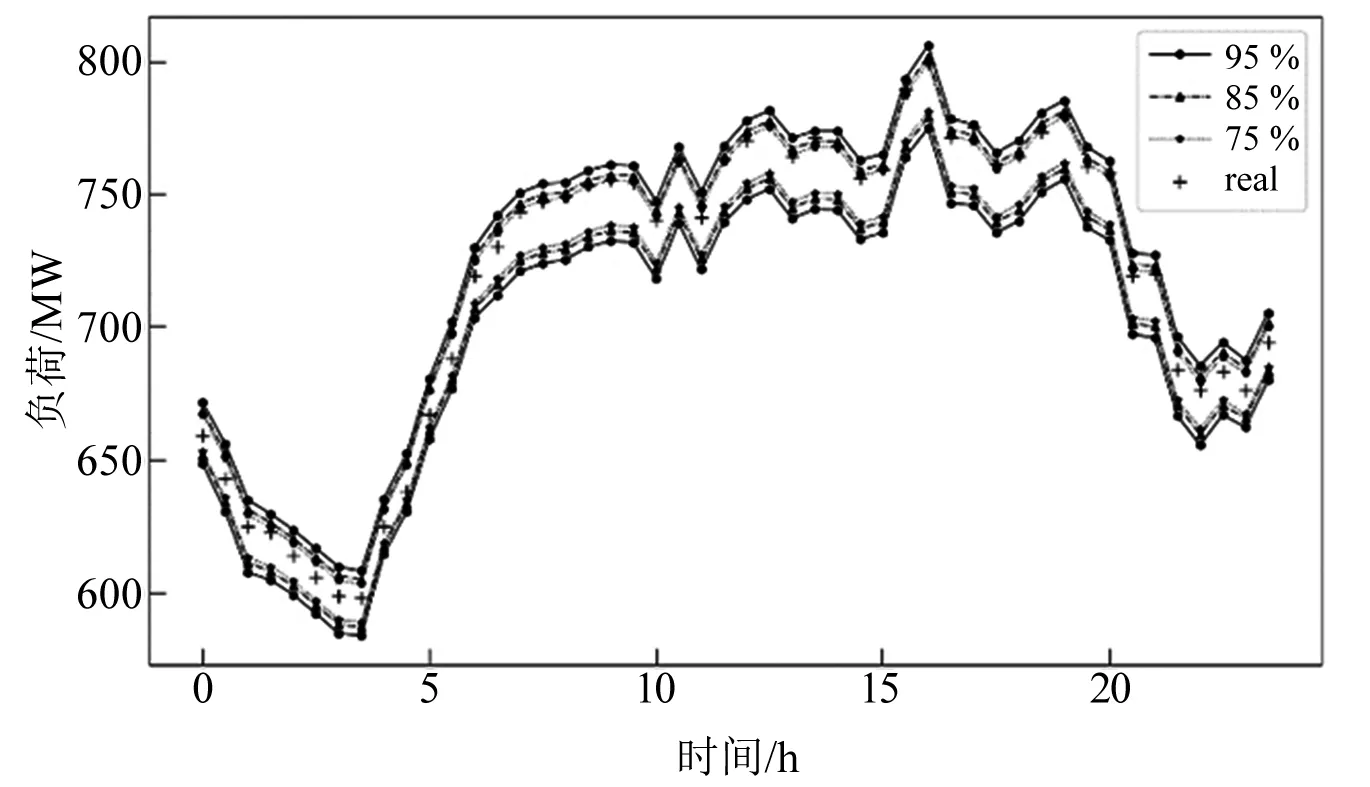
图9 B-LSTM区间预测

4 结束语

本文提出Bootstrap-LSTM方法进行区间预测，通过试验可知，提出的区间预测模型在所有对比算法中CWC值最小，说明所提模型在对比算法中最优。但区间预测模型仍需改进，如监督学习算法SVR与半监督学习算法LSTM的预测结果在PICP、MPIW评价指标表现上各有优势，用PICP指标评价这两个模型则LSTM优于SVR方法，而用MPIW指标评价模型则SVR方法更优。但希望的理想模型是PICP值尽可能大，同时MPIW值尽可能小，这也是区间预测方法未来需要改进的方向。

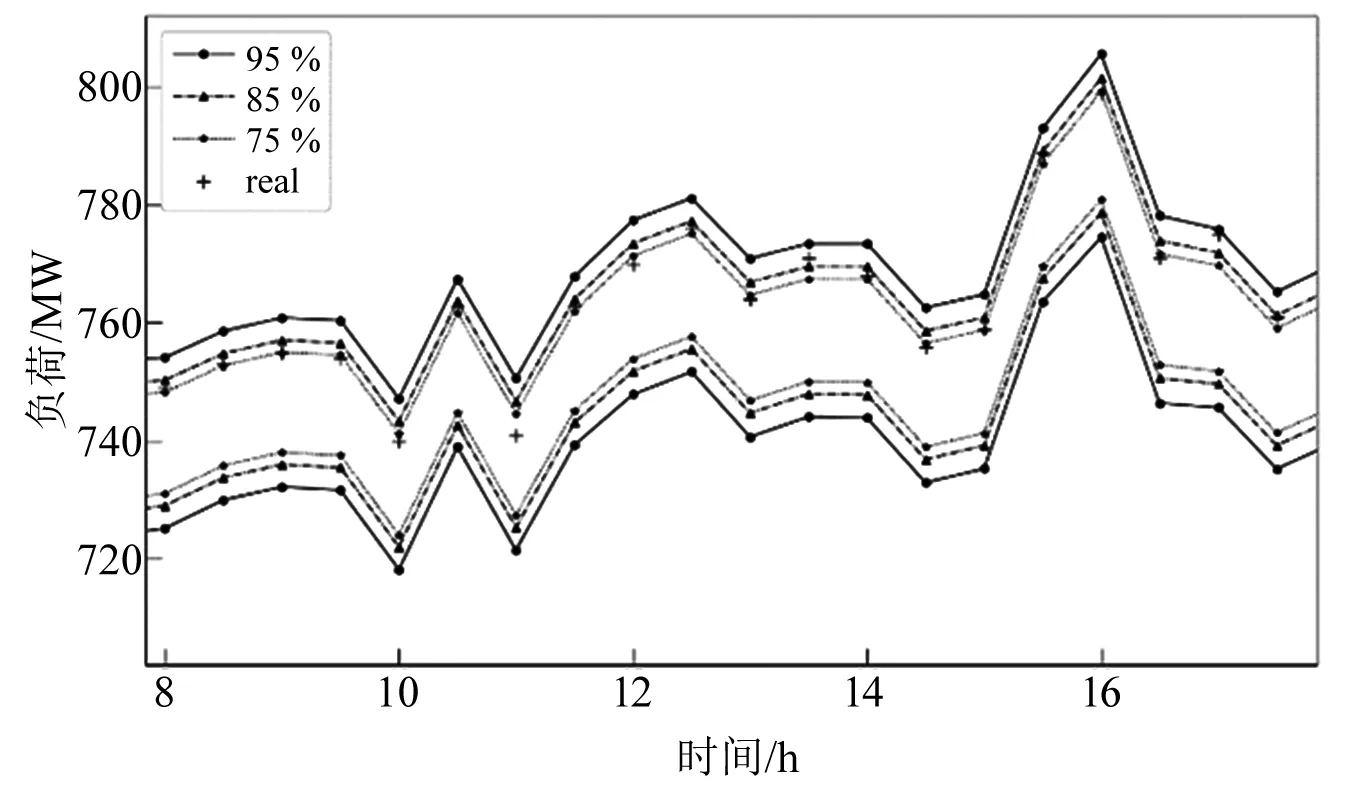
图10 B-LSTM区间预测局部放大图

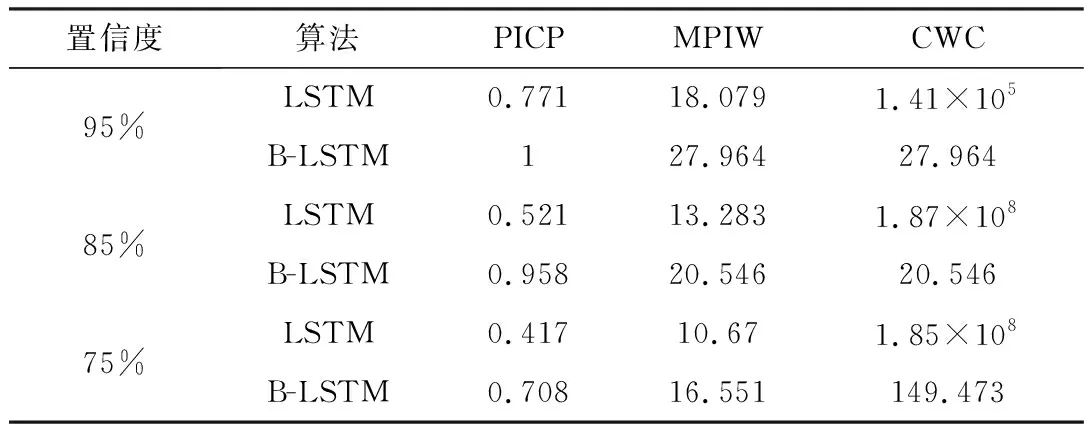
表2 不同模型区间预测指标对比