考虑微凸体侧接触的结合面法向接触刚度建模

王世军,杨昭,吴敬伟,李鹏阳

(1.西安理工大学机械与精密仪器工程学院,710048,西安;2.西安昆仑工业(集团)有限责任公司技术部,710043,西安)

在结合面的接触刚度研究中,通常将微凸体之间的接触视为峰对峰的正接触,这种方法的缺点是不能充分考虑到微凸体侧接触对于整个结合面接触刚度的影响。结合面中的微凸体之间的接触,大多为侧接触,而非正接触[1],通过只考虑微凸体正接触获得的两个结合面之间的接触刚度模型,与实际有一定差别。

在微凸体侧接触研究中,Gorbatikh假设了接触角度θ的分布函数[1]。Sepehri和Farhang(SF模型)将微凸体假设为椭球体,研究了微凸体之间侧接触对结合面接触特性的影响[2-3]。庄艳和朱林波补齐了微凸体接触状态中的弹塑性阶段,并对基于不同模型下的微凸体侧接触状态进行了对比[4-5]。ZHAO等基于微凸体侧接触模型,通过模拟微凸体真实接触,再结合统计方法,得到两个接触面的法向接触刚度[6]。高志强(GZQ模型)基于Gorbatikh提出的接触角度分布规律,构建了结合面间的接触能耗模型[7]。

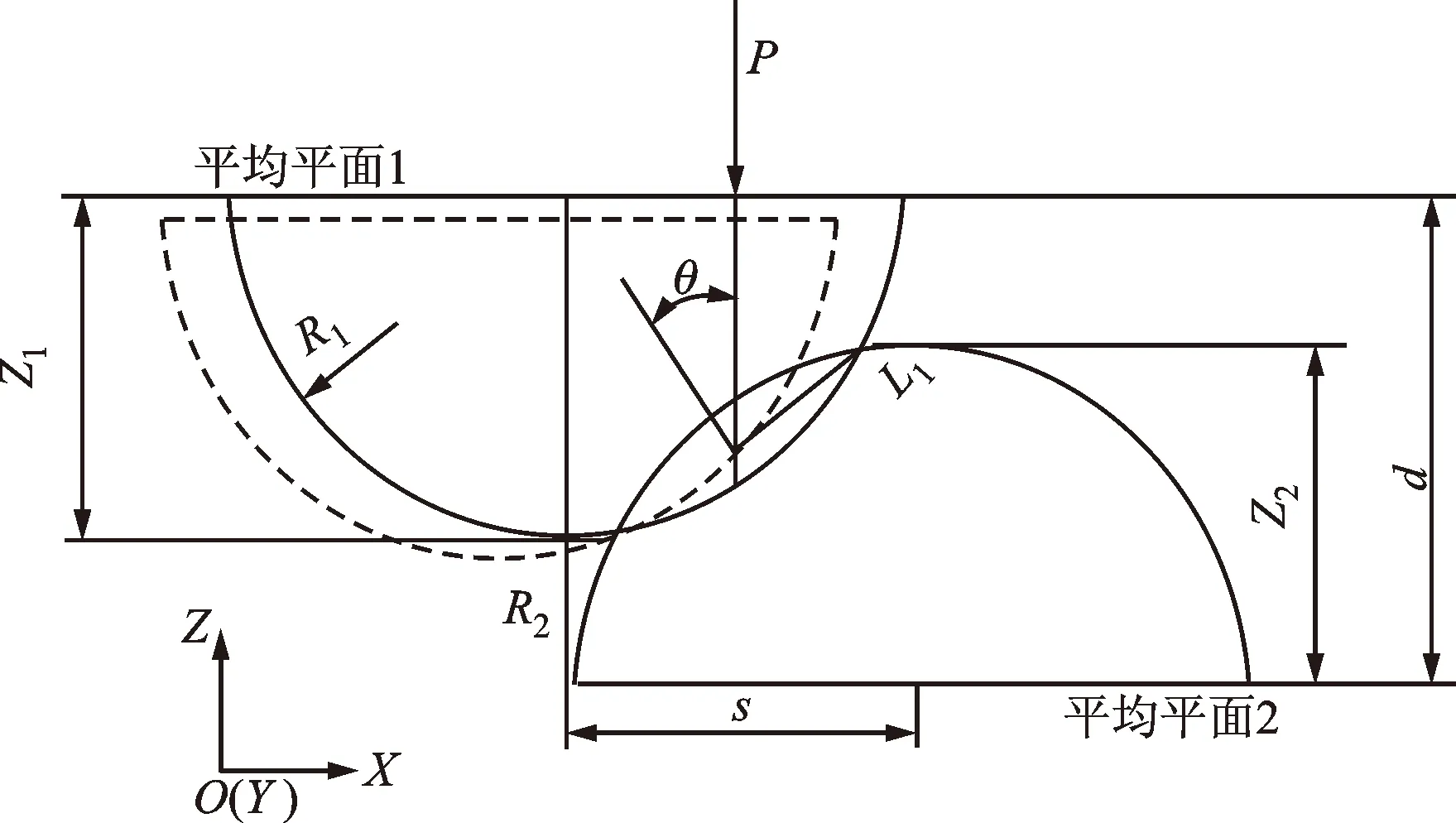
图1 微凸体侧接触模型Fig.1 Side contact model of asperities

上述研究都存在一个问题:如图1所示的微凸体侧接触模型,微凸体中心水平距离s和接触角θ并不是单独存在,两者之间应该有一定的关系。在目前的研究中,都是将参数设为固定值来研究结合面之间的接触特性,这显然不符合实际。在结合面中的微凸体中心水平距离s并不是定值分布,接触角度θ也不是定值,而是跟s的变化有关系。虽然Gorbatikh假设了接触角度θ的分布函数,并没有给出理论依据,也未曾做过试验来证明假设的分布函数的合理性和正确性。

综上,本文采集了接触试样的表面轮廓,分析了微凸体水平距离的分布规律,并提出了一种考虑微凸体水平距离分布的侧接触结合面的法向刚度建模方法。

1 微凸体中心水平距离分布规律

通过图2所示的Keyence的超景深三维显微系统VHX-5000获取磨削试样的三维轮廓数据,采样间隔在x、y方向均为1 μm,对获取的数据进行处理,使得高度方向的均值为0,图3和图4为样本表面的轮廓。

图2 超景深显微系统VHX-5000Fig.2 Ultra-depth of field microscopy system VHX-5000

图3 上试样表面轮廓图Fig.3 Surface profile of the upper sample

根据获取的三维轮廓数据,在上、下试样分别选取6个断面上的二维轮廓数据点,采样长度为1 000 μm,如图5～图16所示。

图4 下试样表面轮廓图Fig.4 Surface profile of lower sample

图5 上试样第1组随机二维轮廓线Fig.5 First set of random two-dimensional contours of upper sample

图6 下试样第1组随机二维轮廓线Fig.6 First set of random two-dimensional contours of lower sample

图7 上试样第2组随机二维轮廓线Fig.7 Second set of random two-dimensional contours of upper sample

图8 下试样第2组随机二维轮廓线Fig.8 Second set of random two-dimensional contours of lower sample

图9 上试样第3组随机二维轮廓线Fig.9 Third set of random two-dimensional contours of upper sample

图10 下试样第3组随机二维轮廓线Fig.10 Third set of random two-dimensional contour lines of lower sample

图11 上试样第4组随机二维轮廓线Fig.11 Fourth set of random two-dimensional contours of upper sample

图12 下试样第4组随机二维轮廓线Fig.12 Fourth set of random two-dimensional contours of lower sample

图13 上试样第5组随机二维轮廓线Fig.13 Fifth group of random two-dimensional contours of upper sample

图14 下试样第5组随机二维轮廓线Fig.14 Fifth group of random two-dimensional contours of lower sample

图15 上试样第6组随机二维轮廓线Fig.15 Sixth group of random two-dimensional contours of upper sample

图16 下试样第6组随机二维轮廓线Fig.16 Sixth group of random two-dimensional contours of lower sample

采用“一峰对两峰”的形式,获取微凸体中心水平距离,如图17所示。

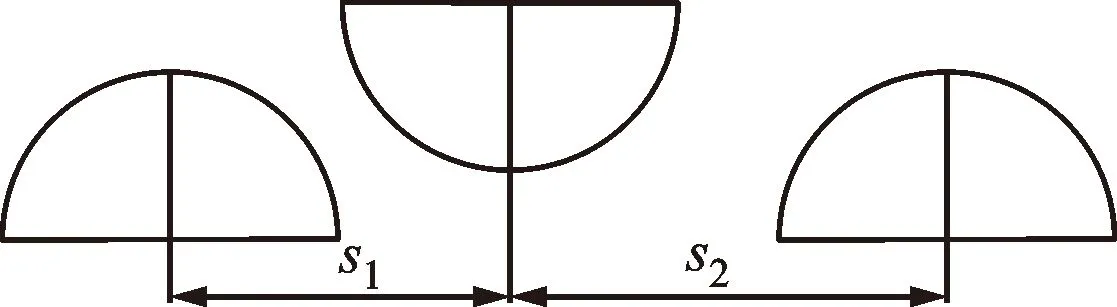
图17 采用“一峰对两峰”的形式获取微凸体中心水平距离Fig.17 The horizontal distance of the center of the micro convex body is obtained in the form of “one peak to two peaks”

采用“三点峰”[8]的形式读取各断面上的二维轮廓峰值点及其坐标。以上试样的峰为基准,采取下、上试样离该峰最近的一左一右的两个峰值点及其坐标,则上试样峰与下试样的两个峰之间的横坐标差值就是两个微凸体中心的水平距离。根据3个峰的坐标点数,左边两个微凸体之间的水平距离s1为正值,右边的微凸体距离s2为负值,正、负号只代表距离方向。

得到6组微凸体中心距离之后,对距离分布图进行数据拟合,发现近似呈正态分布,如图18～图23所示。

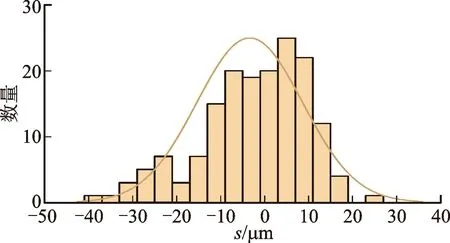
图18 第1组微凸体中心距离分布Fig.18 Center distance distribution of first group of asperities

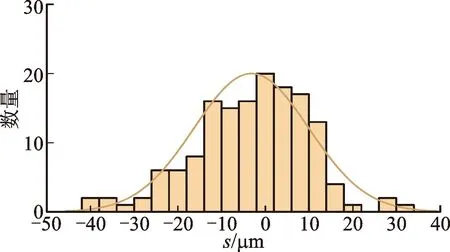
图19 第2组微凸体中心距离分布Fig.19 The distance distribution of the center of the second group of asperities

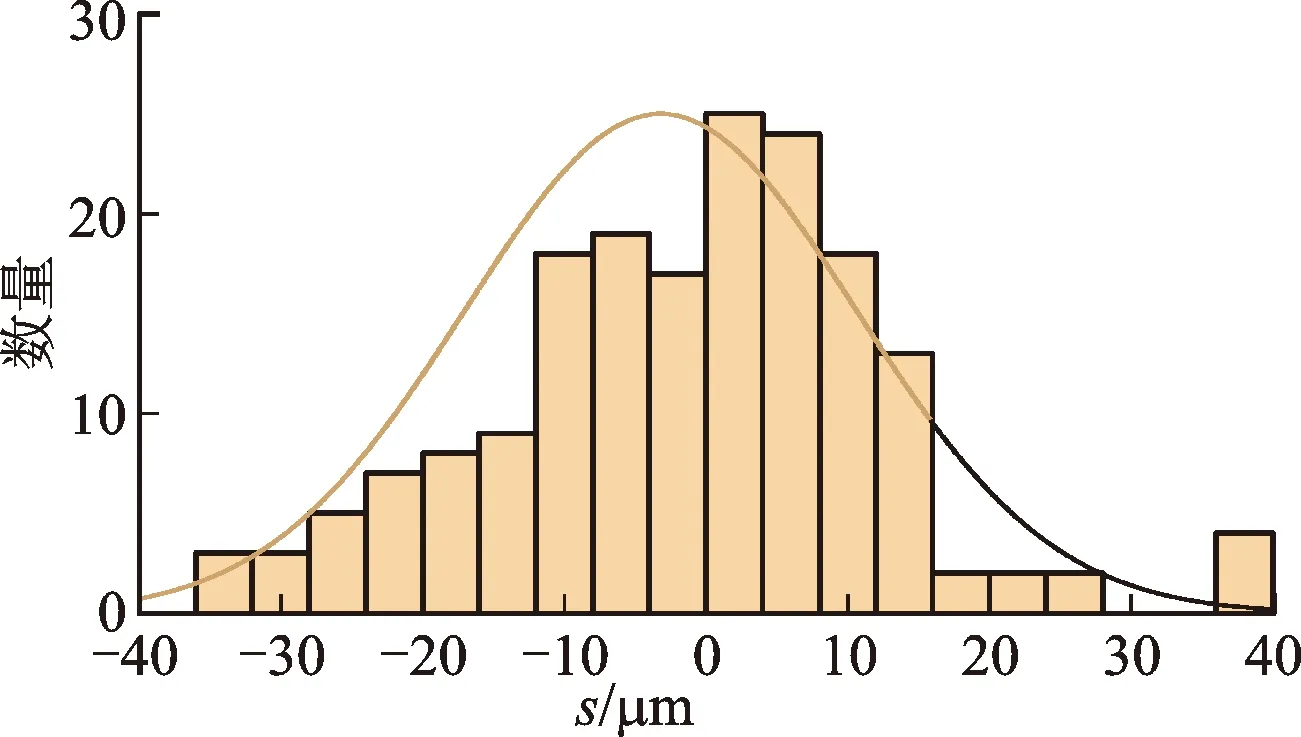
图20 第3组微凸体中心距离分布Fig.20 Third group of micro convex center distance distribution

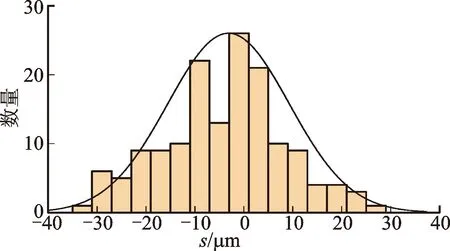
图21 第4组微凸体中心距离分布Fig.21 Center distance distribution of fourth group of asperities

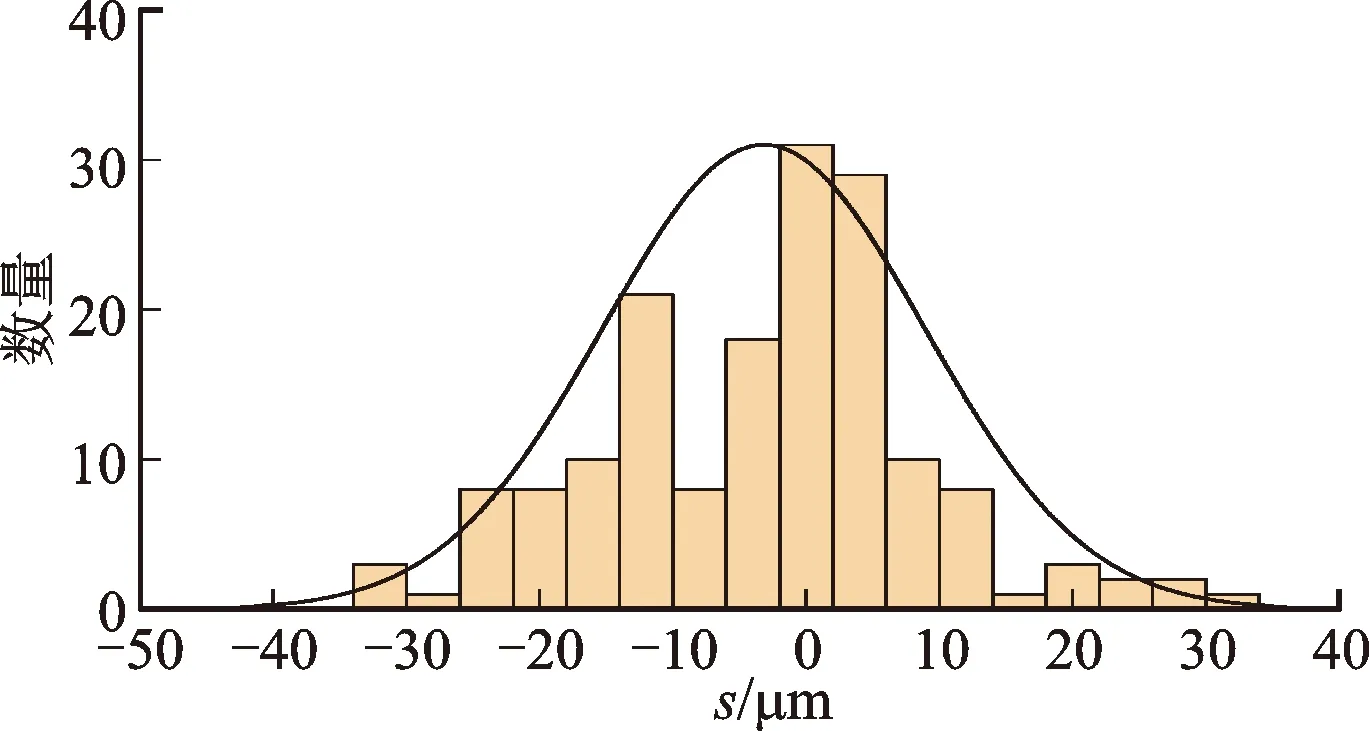
图22 第5组微凸体中心距离分布Fig.22 The center distance distribution of the fifth group of asperities

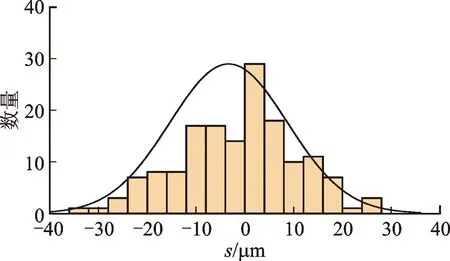
图23 第6组微凸体中心距离分布Fig.23 Center distance distribution of sixth group of micro-convex bodies

正态分布的概率密度函数为[9]

(1)

式中:σ′为微凸体中心水平距离的标准偏差,分布曲线的幅度由其决定;μ′为微凸体中心水平距离的均值,决定着分布曲线的位置。

从图18～图23可以看出,微凸体中心水平距离分布并不是呈左右对称的,而是向某一侧有偏斜,这种不对称用偏斜度Rsk来度量,计算公式[10]如下

(2)

式中:n为样本个数;σs为微凸体中心水平距离的标准偏差;μs为微凸体中心水平距离平均值。

偏斜度Rsk可以为正值也可以为负值,如果偏斜度为0,说明微凸体水平距离分布对称且均匀。如果粗糙表面侧接触的微凸体水平距离分布不对称或者不均匀,微凸体水平距离的分布曲线的偏斜度Rsk就是正值或负值。

峰度是反映一组数据的平均值所处的峰值高低,公式[9]为

(3)

峰度和偏斜度是检验一组分布数据跟正态分布之间的偏离程度,也是判断该组数据是否近似正态分布的重要判断依据。

偏度系数和峰度系数检验公式如下[11]

(4)

(5)

当zsk、zku绝对值小于1.96时,即显著等于0,也就是该组数据呈正态分布,正态分布假设得到验证。

由式(4)(5)计算得出,采样间隔为1 μm的微凸体水平距离分布曲线的偏斜度系数和峰度系数如表1所示。由表中数据可以看到偏度系数为0.634,峰度系数为0.576,因此可以认为微凸体中心水平距离分布近似呈正态分布。

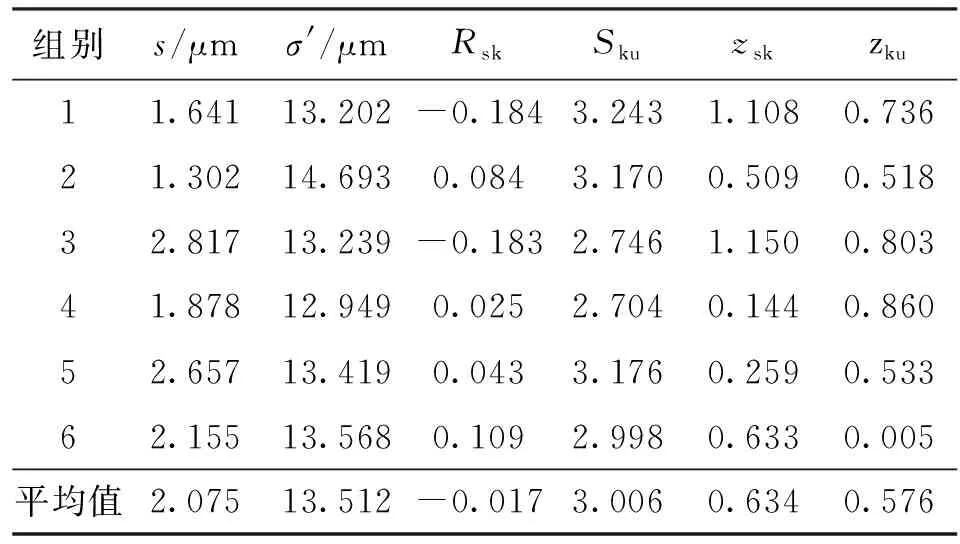
表1 采样间隔为1 μm微凸体中心水平距离分布统计

2 微凸体侧接触模型

将结合面的微凸体等效为球体,在法向力P作用下,接触情况如图24所示。其中Z1和Z2为两微凸体的高度,R1和R2为两微凸体的曲率半径,s为两微凸体的中心水平距离,θ为微凸体之间的接触角,d为结合面的平均间距。将两个微凸体的接触表面作为一个基准,建立OX′Y′Z′坐标系,以Z′方向为法向,以Y′方向为切向,则法向作用力可以分解为沿Z′方向的Pn和沿X′方向的Pτ。在Pn作用下,微凸体在Z′方向发生变形,变形量为δZ′;在Pτ作用下,微凸体在X′方向发生滑移,滑移量为ζX′。将结合面当做一个基准,建立OXYZ坐标系,令结合面法向为Z轴,结合面切向为X轴。ζZ为ζX′相对在Z轴上的变形量,δZ为δZ′相对在Z轴上的变形量,则在Z轴的总变形量为δ。

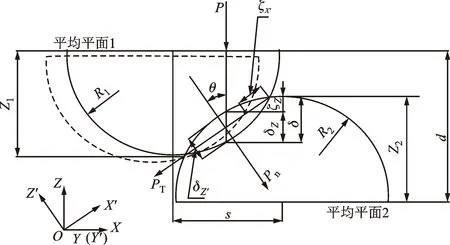
图24 微凸体侧接触示意图Fig.24 Schematic diagram of side contact of asperity

根据几何关系,可知

(6)

(7)

δZ=δZ′cosθ

(8)

ζZ=ζX′sinθ

(9)

(10)

式中:Rs=R1+R2。微凸体上的受力满足

Pτ=Pntanθ

(11)

P=Pncosθ+Pτsinθ

(12)

2.1 弹性阶段

在Z′方向,当微凸体变形量0≤δZ′<δZ′ec时,进入弹性阶段,δZ′ec为临界变形量,表达如下

(13)

式中:E为当量弹性模量;K=0.454+0.41ν,其中ν为泊松比;H为硬度。E、H都取材料中相对较软的一方的值。

根据赫兹理论[12],法向分力Pn与Z′方向上变形量δZ′之间的关系为

(14)

切向分力Pτ为

(15)

则法向合力为

Pe=Pnecosθ+Pτesinθ=

(16)

根据Pn=Pcosθ,可获得弹性阶段Z′轴方向的变形量相对与Z轴方向的总变形量δZ′e=δecos3/2θ,则法向合力为

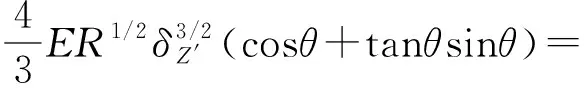
(17)

微凸体在该阶段内接触刚度为

(18)

2.2 塑性阶段

根据文献[12]可知,当微凸体变形量δZ′<110δZ′ec,进入塑性阶段。此时,单对微凸体的法向分力与变形之间的关系为

Pnp=2πHRδZ′

(19)

切向分力为

Pτp=Pnptanθ=2πHRδZ′tanθ

(20)

法向合力为

Pp=Pnpcosθ+Pτpsinθ=

2πHRδZ′(cosθ+tanθsinθ)

(21)

根据Pn=Pcosθ,可获得弹性阶段Z′轴方向的变形量相对与Z轴方向变形量的关系δZ′p=δpcosθ,则法向合力为

Pp=Pnpcosθ+Pτpsinθ=

2πHRδZ′(cosθ+tanθsinθ)=

(22)

则在塑性阶段微凸体的接触刚度为

(23)

2.3 弹塑性阶段

根据KE模型[13],当微凸体变形量δZ′ec≤δZ′<110δZ′ec,微凸体进入弹塑性阶段。

文献[13]中,当δZ′ec≤δZ′<6δZ′ec时,弹塑性区分为Ⅰ区,有

(24)

当6δZ′ec≤δZ′<110δZ′ec时,弹塑性区又可分为Ⅱ区,有

(25)

本文弹塑性Ⅰ区,法向分力为

(26)

Pτep1=Pnep1tanθ=

(27)

则在弹塑性Ⅰ区的法向合力为

Pep1=Pnep1cosθ+Pτep1sinθ=

(28)

根据Pn=Pcosθ,可获得弹性阶段Z′轴方向的变形量相对Z轴方向变形量的关系δZ′ep=δepcos1/1.425θ,则法向合力

Pep1=Pnep1cosθ+Pτep1sinθ=

(29)

弹塑性Ⅰ区的接触刚度为

(30)

同理,可得弹塑性Ⅱ区的接触刚度为

(31)

3 结合面间的法向接触刚度

根据研究表明[10],粗糙峰高度z在接触面上近似呈正态分布

(32)

则结合面间接触的微凸体数量为

(33)

式中:N=Anη;η为粗糙峰密度;An为名义接触面积。

两粗糙表面接触时,微凸体水平距离s分布可以近似看成正态分布,即

(34)

则根据统计理论,可以得到结合面间所有微凸体在3种不同接触状态下的法向接触力,分别为

(35)

(36)

(37)

(38)

(39)

则总的接触载荷P为

P=Pe+Pep1+Pep2+Pp

(40)

结合面在不同状态下的法向接触刚度为

(41)

(42)

(43)

(44)

总的接触刚度K为

K=Ke+Kep1+Kep2+Kp

(45)

为了方便后期模型的计算及验证,需要对建立的新模型进行无量纲化。无量纲化接触载荷P*为

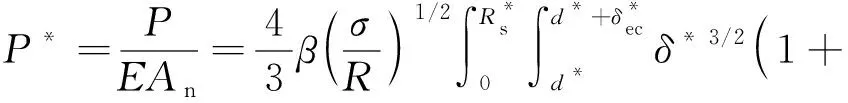
(46)

(47)

式中

(48)

(49)

(50)

4 理论结果与分析

对式(46)(47)进行仿真,并且与GZQ模型和KE模型对比。表面形貌参数β、σ/R都与塑性指数ψ[14]相关,塑性指数ψ是判断微凸体接触变形的重要依据。假设接触面为两钢制物体,所用材料参数[15]分别为E1=E2=207 GPa,H=1.96 GPa,v1=v2=0.29;表面形貌参数为R=2.5 μm,σ′=1.2 μm,ψ与参数β、σ/R之间的关系见表2[16]。

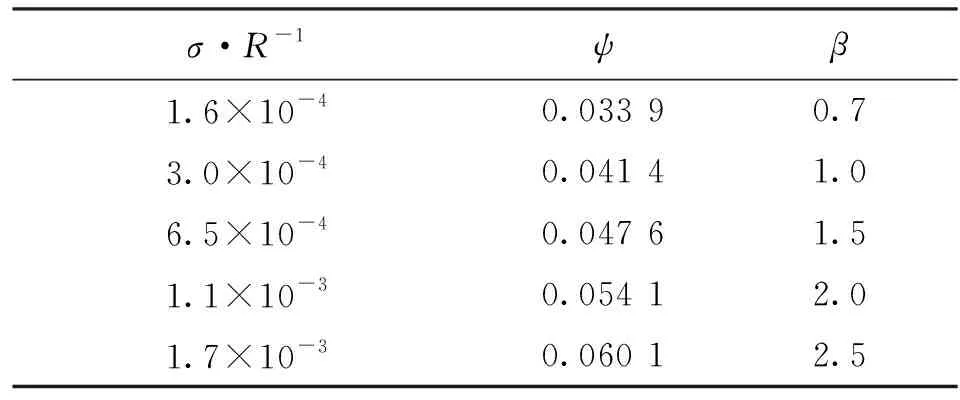
表2 表面形貌参数和可塑性指数

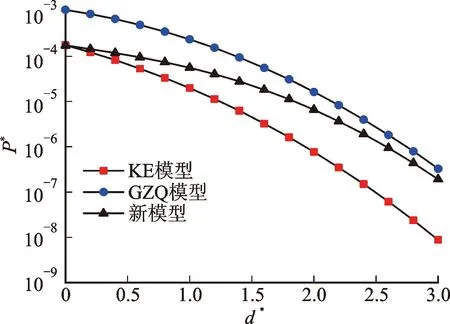
如图25所示,各模型在3种塑性指数下的趋势都是一样的,因为随着d*的增大,两接触表面的距离增大,结合面间接触微凸体数量会减少,因此P*会变小。

(a)ψ=0.7

GZQ模型、KE模型和本文模随着ψ的增加,P*也随之增大。这是因为ψ的增加,越来越多的微凸体会处于弹塑性和完全塑性状态,致使P*增加,这跟实际情况相符。从图25还可以看出,随着结合面平面间距d*的增加,本文模型和KE模型的无量纲法向接触载荷相差越来越大,而在结合面平均间距较少时,两者相差越来越小。这是因为:间距较小时,结合面间接触的微凸体变多,而且接触状态也大多都进入了弹塑性和塑性阶段;随着接触状态由弹性向塑性过渡,微凸体接触角度会越来越接近90°,角度对接触载荷的影响在下降,表现出的就是在间距为0时,两者的接触载荷相差较小。

GZQ模型和本文模型与没有考虑微凸体侧接触的KE模型比较,无量纲接触载荷ψ*都较大。这是因为侧接触中,微凸体接触面不仅存在法向载荷,还存在切向载荷,两者合力为结合面法向接触总载荷。在塑性指数ψ=1.5、d*=0.8时,本文模型、GZQ模型和KE模型预测的P*分别为2.817×10-4、7.364×10-3和1.127×10-4,可以看出,本文模型的预测结果比KE模型别大了149%,比GZQ模型小了161%。

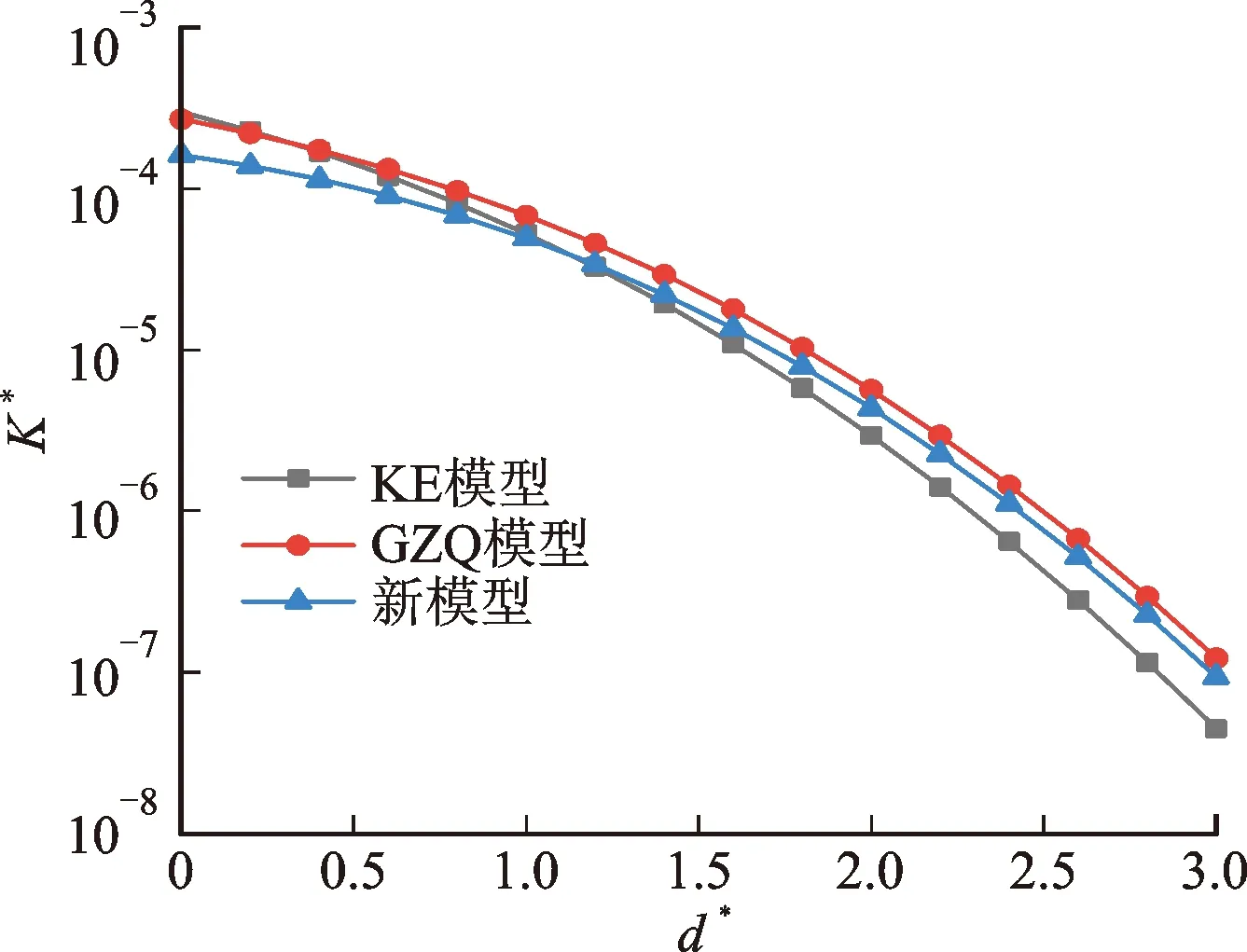
如图26所示,随着d*的增大,K*越来越小,各模型在不同塑性指数下的趋势都是一样的,结合面间接触微凸体数量会减少,结合面的无量纲法向接触刚度变小。

(a)ψ=0.7

在不同塑性指数下,本文模型、GZQ模型都与KE模型在不同的d*下的无量纲接触刚度K*相等。这是因为GZQ模型和本文模型考虑了微凸体侧接触,微凸体侧接触是跟角度和微凸体中心水平距离有关系的,在90°和中心水平距离为Rs时,微凸体侧接触跟微凸体正接触表现一样。即在某个d*下,无量纲接触刚度K*相等。与KE模型相比,GZQ模型和本文模型在d*较小时,接触刚度小于KE模型的接触刚度;在d*较大时,呈现出接触刚度大于KE模型的接触刚度。

在塑性指数ψ=1.5、d*=1.6时,本文模型、GZQ模型和KE模型预测的K*分别为5.43×10-5、6.666×10-5和4.430×10-5,可以看出,本文模型的预测结果分别比KE模型别大了22.5%,比GZQ模型小了22.6%。

5 有限元仿真与试验验证

试验装置如图27所示,由两个半环试样组成。两个半环试样在端面上通过M10螺栓联接起来,形成一个完整的圆环,端面的法向接触压力由螺栓预紧力提供。两个半环试样尺寸相同,内径为275 mm,厚度为35 mm。试验过程中,在两个试样的外圆上布置加速度传感器,通过锤击法获得结构的振型及固有频率。

图27 结合面固有频率测定试验装置Fig.27 Test device for natural frequency measurement of joint surface

在端部结合面上分别施加法向接触载荷0.6、0.8和1 MPa,然后记录试样在3种不同接触载荷下的前三阶振型和固有频率。

图28为通过ANSYS软件建立的有限元模型。为了引入新的接触刚度解析模型,应用虚拟材料法[17-21]模拟结合面之间的接触特性,在半环的接触区域构建一个含有虚拟材料的薄层。半环试样模型选取solid185单元,总数为99 866个。由不同的理论接触模型计算出接触刚度,再通过参数设计语言APDL语言导入虚拟材料中,供有限元分析使用。有限元分析中的材料参数和试验材料参数保持一致,如表3所示。

图28 包含结合部的有限元模型Fig.28 Model including joints

表3 接触试样的材料参数

根据文献[22-24]方法得到的接触表面的轮廓统计参数为:表面轮廓高度偏差σ=1.01 μm,曲率半径R=4.3 μm,微凸体中心水平距离分布偏差σ′=12.1 μm,塑性指数ψ=40。根据这些统计参数和所施加的法向面压力,利用本文模型就可以计算出表4所示的法向接触刚度Kn。为了对比,表4中也列出了KE模型和GZQ模型的法向接触刚度。

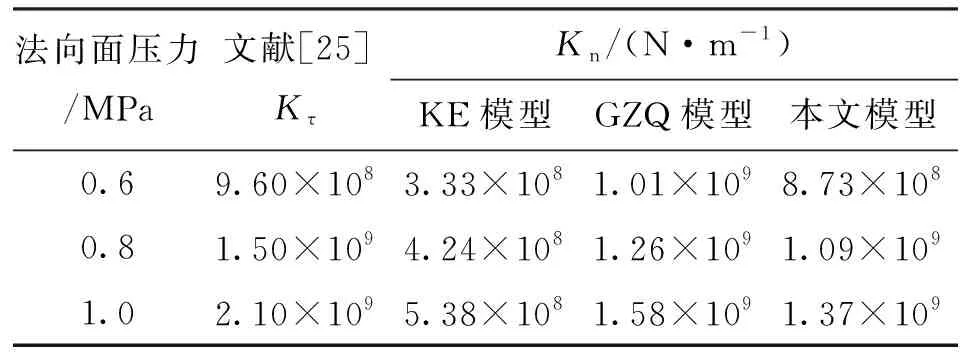
表4 结合面接触刚度

采用文献[25]所建立的切向刚度模型获得切向接触刚度Kτ。通过功率谱密度法获取本文试样表面轮廓的分形参数,试样的分形参数D为1.809,G为1.302×10-11,将其代入文献[25]的切向刚度模型,即可获得表4所示的切向刚度Kτ。

法向面压力为0.6 MPa时,本文模型与试验模型固有频率的对比见图29。

(a)一阶振型

如表5所示,在不同法向面压力下,本文模型仿真得到的固有频率与试验固有频率之间的最大相对误差为8.2%,GZQ模型仿真的最大相对误差为17.64%,KE模型仿真的最大相对误差为18.9%。

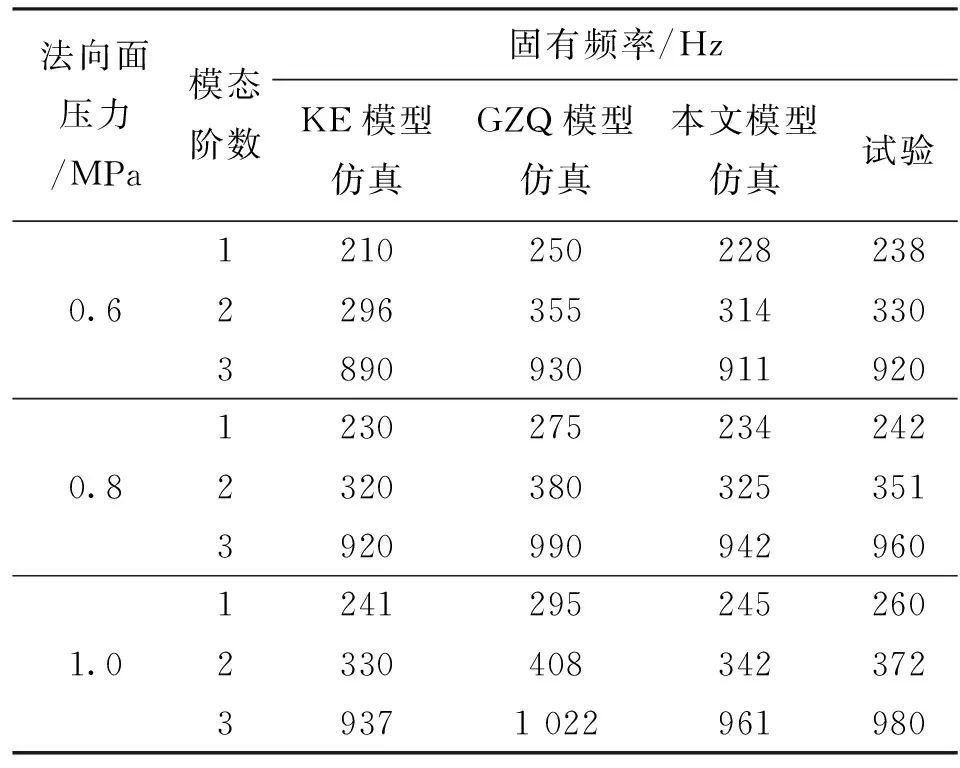
表5 不同模型的仿真和试验固有频率对比

6 结 论

(1)微凸体侧接触中,微凸体中心水平距离分布规律影响着最终扩展到结合面上的接触特性。本文对接触表面的微观形貌进行的研究表明,微凸体中心水平距离近似呈正态分布。

(2)基于统计理论和微凸体水平分布规律建立的本文模型与其他两种模型进行的对比发现,本文模型相较于KE模型,法向接触刚度呈现出先减小后增加的趋势,相较于GZQ模型,法向接触刚度则小于GZQ模型。

(3)有限元分析和试验结果显示,本文模型与GZQ模型和KE模型相比,固有频率与试验值的相对误差最小,证明本文模型更符合实际,能更准确地预测结合面间的法向接触特性。