具有休假的退化可修系统维修策略研究

李延玲, 傅 华

(1.青海民族大学 数学与统计学院,西宁 810007；2.福建警察学院，福州 350007)

近年来,随着经济的快速发展,对系统可靠性提出了更高的要求,因为有些系统一旦发生发生故障,将会造成不同程度的损害,如信号灯设备系统的不可靠会导致动车追尾事故,导航系统的不可靠可能会导致飞机坠毁等等.因此,在走向现代化的过程中,在各个方面提高和改善系统的可靠性越来越受到重视,在这方面的研究[1-5].为了提高系统的可靠性,系统的维修策略成为了重要的研究内容[6-11],本文讨论了带有单重休假的两相同部件冷储备系统的维修策略,假设两个部件故障之后都不能修复如新,特别的,由于修理工带有单重休假,故两部件故障之后,如果修理工休假结束在系统时,则故障部件就会立即得到修理;如果修理工正在休假,则故障部件的修理就会被延迟.在如上假设下,研究了基于部件1故障次数的N策略替换(在一个更新周期内部件1和部件2的故障次数是相当的).

1 数学模型

这部分关于退化系统中几何过程的定义可以参考文献[1]，下面给出关于该模型的基本假设：

假设1 系统是由两相同部件构成的冷备系统，修理工带休假，刚开始部件1工作，部件2冷储备，修理工开始休假；

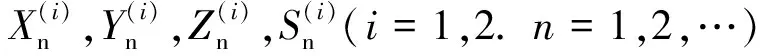
Hn(t)=1-exp(-vt)，

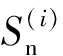
假设3 根据部件1故障次数实行N策略替换,即,当部件1的故障次数达到N*时，系统被替换.

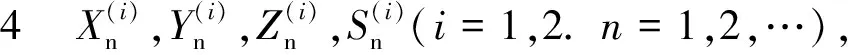
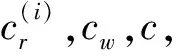
由系统假设条件及分析，该系统可能的运行过程如图1所示.

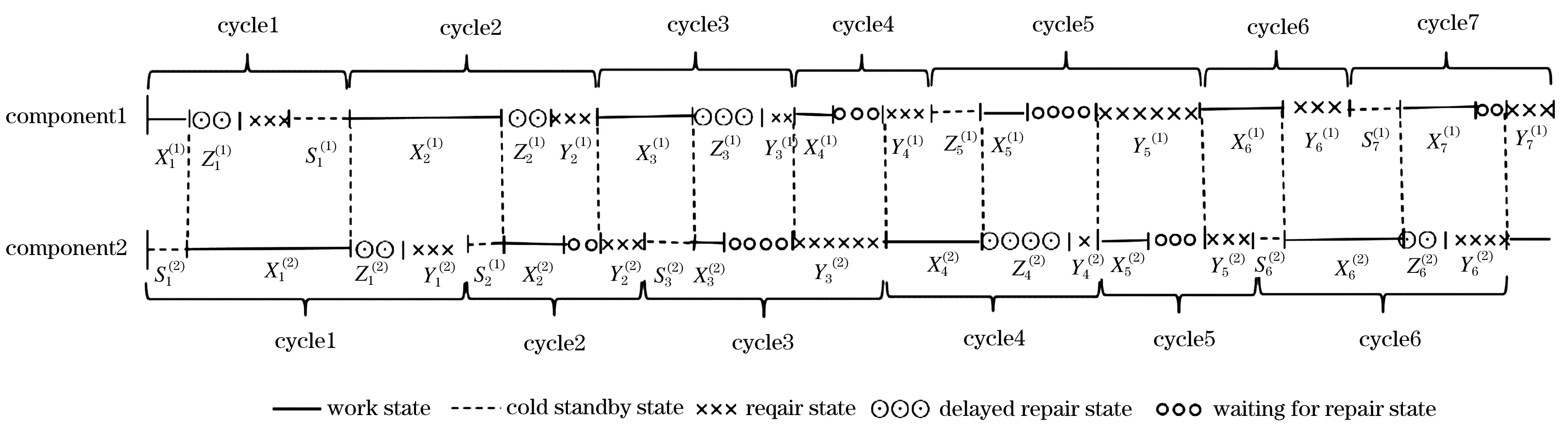
图1 两相同部件的冷储备系统的运行过程Figure 1 Apossible course of the cold standby system with two similar components

说明 假设条件3中提到的系统替换是指部件1和部件2同时替换，因为从系统的进程图1可以看到，在一个更新周期内部件1和部件2的故障次数是相当的，所以基于部件1的故障次数实行N策略替换是合理的.

2 N策略

设τ1为系统的第一次更换时间,τn为系统第(n-1)次更换完成与第n次更换完成之间的时间间隔, {τ1,τ2,…}形成了一个更新过程.则由更新理论得到在N策略下系统平均费用C(N)：

(1)

其中:D和W分别表示更新周期内的平均费用和平均长度, 由系统的工作进程可得如下表达式：

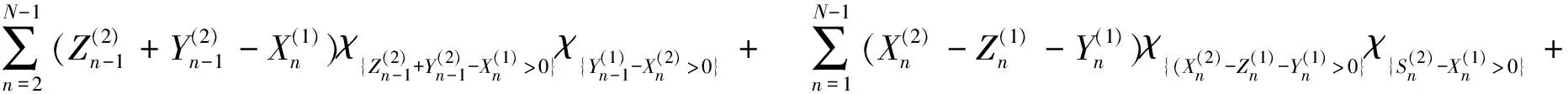
(2)

由假设条件可知：

(3)

进一步，由卷积定义得如下变量所对应的分布函数：

[1-F(-an-1t)]

从而有

(4)

将式(3)、(4)代入(2)式得到：

(5)

通过假设条件及图1的分析，系统总的工作时间如下：

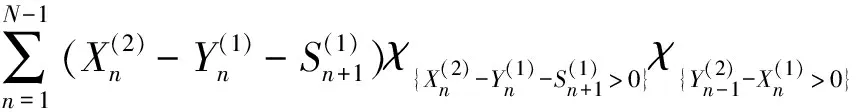
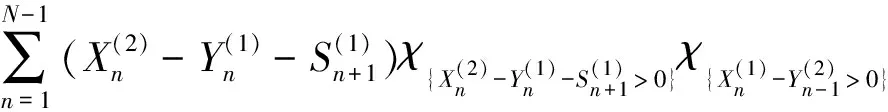
从而有

(6)

将式(5)、(6)带入式(1)得到系统在N策略下平均费用C(N)的精确表达式：

(7)

其中,

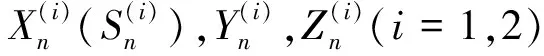
ψn(t)=gn-1(t)*sn(t)*fn(-t)=

ωn(t)=gn-1(t)*sn(t)*hn-1(t)*fn(-t)=

kn(t)=zn-1(t)*gn-1(t)*fn(-t)=

pn(t)=fn(t)*gn(-t)*zn(-t)=

wn(t)=fn(t)*gn(-t)*sn+1(-t)=

rn(t)=fn(t)*zn(-t)*gn(-t)*sn+1(-t)=

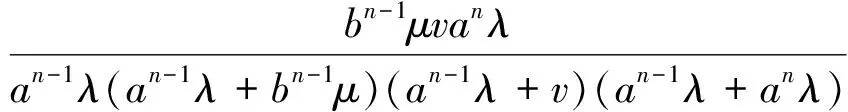
最后, 由以上结果及假设条件2,式(7)为：

C(N)=

(8)

其中，

进一步,为了说明N*的存在性与唯一性，给出如下参数值：

a=1.1,b=0.9,λ=0.01,μ=0.1,v=0.11,cr=10,c=2 500,cw=9

将如上参数值带入式(8)，见表1.

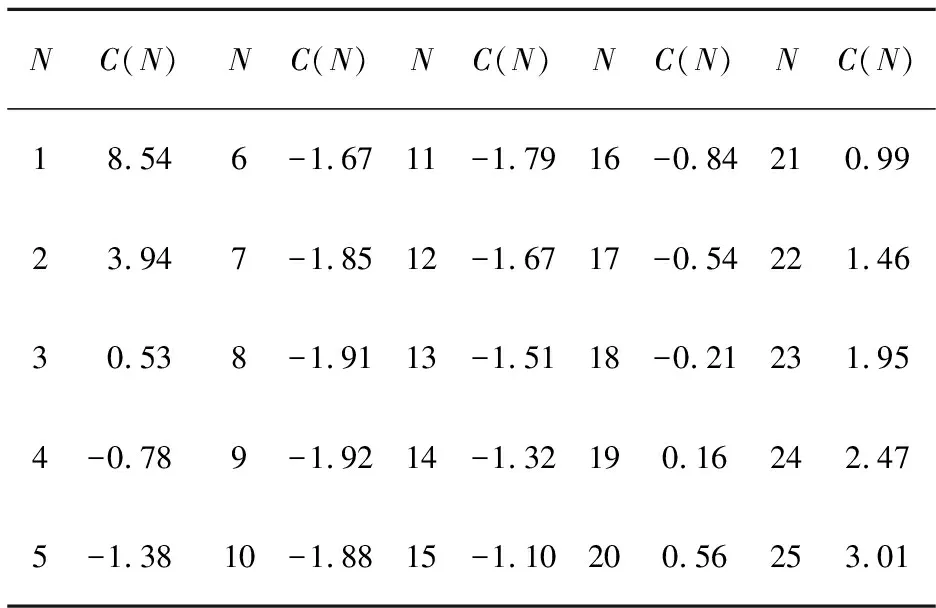
表1 系统的平均费用率C(N)

从表1可以看出系统的最优替换策略N*=9存在且唯一,相应的费用C(N*)=-1.92最少, 也就是说, 当部件的故障次数达到9次时,系统中部件1和部件2将同时被替换， 此时系统费用最少。

3 结 语

本文主要研究带有单重休假的两相同部件冷储备系统的维修策略,假设系统中的两相同部件故障后都不能修复如新，由于修理工带有单重休假，故部件故障后的修理有可能延迟也有可能不延迟，基于以上假设，主要研究了基于部件1的故障次数的维修策略(部件1和部件2在一个更新周期内的故障次数是相当的)，并通过数值分析找到了系统的最优替换策略N*，当部件1 的故障次数达到N*时，整个系统将被替换。