模糊随机BAM神经网络的固定时间同步
刘 宇,刘 铭
(东北林业大学 理学院,哈尔滨 150040)
1988年,Kosko提出了双向联想记忆神经网络,简称为BAM神经网络[1].BAM神经网络具有较为复杂的结构,其神经元分布在两层里,每一层中的每一个神经元都与另一层中的所有神经元相连接,而同一层中的所有神经元之间则互不连接.在此基础上,Yang[3]等人在1996年将模糊逻辑加入到神经网络中,构造了模糊神经网络,由于其在模式识别等领域有广泛的应用,因此有许多学者对其进行了深入的研究[4].此外,在实际系统中,不可避免地会受到白噪声的干扰,因此有许多学者研究了带有随机扰动的BAM神经网络的动力学行为[5-9].同步作为神经网络的一种重要的动力学行为,有很多学者对其进行了研究,早期研究了指数同步[10]和渐近同步[11],上述两种同步只能在无限时间内达到,然而许多实际系统要求在有限时间内达到同步,因此人们进一步研究了有限时间同步[12],但是有限时间同步的不足在于其收敛时间依赖于系统的初值,使得在应用中不可避免的要计算系统的初始值,但许多系统的初值难以测量,因此学者们开始研究了一种特殊的有限时间同步即固定时间同步[13].固定时间同步既可以使系统在有限时间内达到同步,而且其收敛时间只与一些参数有关,而与系统的初值无关.
基于以上,本文将研究带有随机扰动的时滞模糊BAM神经网络的固定时间同步,所构建的网络模型如下:
(1)
其初值为
(2)
系统(1)由两层组成,即x层和y层,xi(t)表示x层中的n个神经元的膜电位,yj(t)表示y层中的m个神经元的膜电位.τ是离散时滞,αi>0和βj>0其中i=1,2,…,n,j=1,2,…,m表示神经元的自抑制率,f(·)和g(·)表示激活函数,aji,bji,rij,hij表示连接权重,cji和kij是t时刻的模糊反馈最小模板元素,dji和lij是t时刻的模糊反馈最大模板元素,Gji和Wij时刻t的模糊前馈最小模板元素,Jji和Qij时刻t的模糊前馈最大模板元素,∧和∨分别记作模糊AND和模糊OR算子,pj和qi分别为第j个和第i个神经元的输入量,Ai和Bj表示外部输入,σi和σj是白噪声强度.将此系统作为驱动系统,则相应受控的响应系统为:
(3)
其初值为:
(4)
(5)
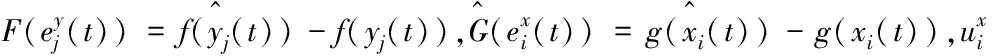
(6)
其中:κi,ωji,μi,ηi,χj,γij,ϖj,ζj是大于0的常数,0<δ<1,λ>1.
1 准备工作
下面给出本文将用到的定理、定义和基本假设.
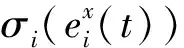
假设2:激活函数f(·)和g(·)满足有界性和Lipschitz条件,对于任意的s1,s2∈R+,存在常数L1>0,L2>0使得:
f(s1)-f(s2)≤L1|s1-s2|,
g(s1)-g(s2)≤L2|s1-s2|
(7)
引理1[14]:假设x1和x2是系统(1)的两个状态,那么我们有:
(8)
引理2[15]:如果p1,p2,…,pn≥0,并且0<δ<1,λ>1,那么以下不等式成立,
(9)
引理3[16]: 对于系统
dx(t)=f(t,x(t))d(t)+g(t,x(t))dB(t),
(10)
其初值x0(t)>0,为如果存在正定的且径向无界的Lyapunov函数V(t,x(t))∈C2,1(n×+,+),并且存在实数ξ1>0,ξ2>0,0<δ<1,λ>1,对于V(t,x(t))∈C2,1(n×+,+)有
LV(x)≤-ξ1Vδ(x)-ξ2Vλ(x),
那么我们就说系统的零解是依概率随机固定时间稳定的,且有
Tò=
定义1:对于系统(10)的任意初值x0(t)>0,存在给定的常数Tmax,M使得以下条件成立:
1)系统的零解是依概率有限时间稳定的;
2)稳定时间T(x0,B)的数学期望是以M为界的并且不依赖于初始条件的,即:Tò=则系统(10)的平凡解是依概率随机固定时间稳定的.
2 主要内容
定理1:设假设1)、2)成立,若以下不等式成立,
Ω1≤0, Ω2≤0, Ω3≤0, Ω4≤0
其中
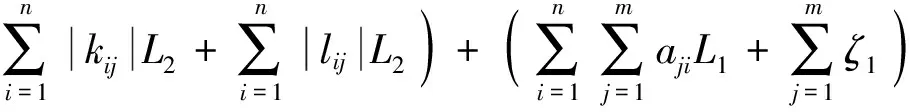
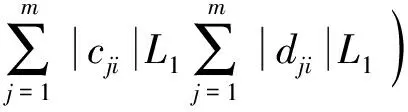
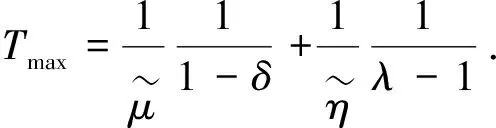
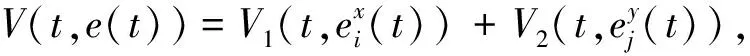
(11)
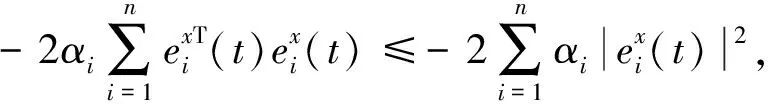
(12)
(13)
因此可得:
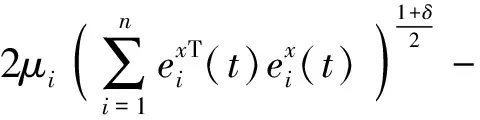
(14)
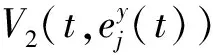
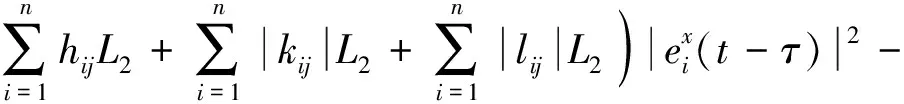
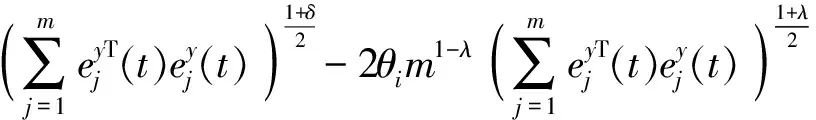
(15)
由以上可得
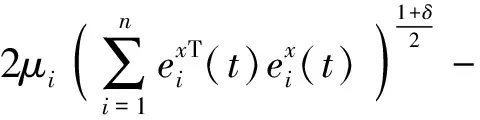
(16)
若定理中的条件成立,则可以得到
(17)
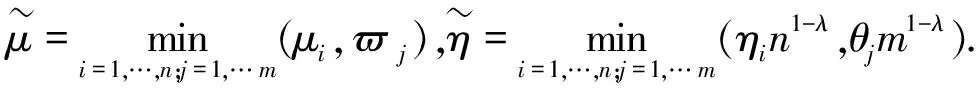
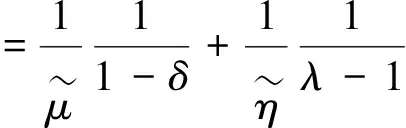
证明完毕.
3 数值模拟
本节对网络和控制器之中的参数取适当的值,利用Matlab软件进行数值模拟,来验证理论结果的有效性.
我们取n=m=6,即每一层网络由六个节点构成,αi=βj=1.7,cji=0.02,dij=0.018,rij=0.5,hij=0.6,kij=0.024,lij=0.022,aji=0.6,bji=0.7,τ=0.1,L1=L2=ζ=ζ1=0.1,κi=χj=50,pi=qj=0.1,ωji=γij=1.1,i,j=1,2,…,6.经过验证,可以知道定理中的条件是成立的.
如下所示,图1、2是驱动系统的两层网络的轨迹,图3、4是响应系统中两层的轨迹,从图中可以看出随机扰动的影响.图5、6分别是误差系统ex和ey的轨迹,可以容易地看出误差系统的轨迹都在固定时间内趋近于0,说明两系统之间的误差趋近于0,两系统达到同步.说明我们设置的控制器是有效的,本文所得到的理论结果是正确的.
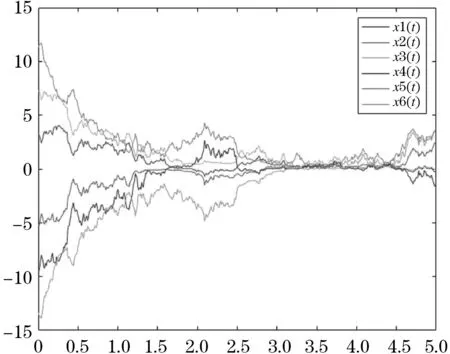
图1 驱动系统x层的轨迹Figure 1 Trajectory of the x-layer of the drive system
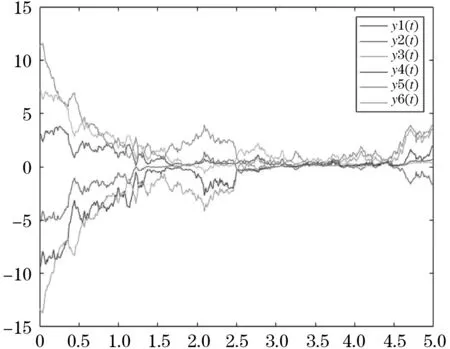
图2 驱动系统y层的轨迹Figure 2 Trajectory of the y-layer of the drive system

图3 响应系统层的轨迹Figure 3 Trajectory of the of the response system
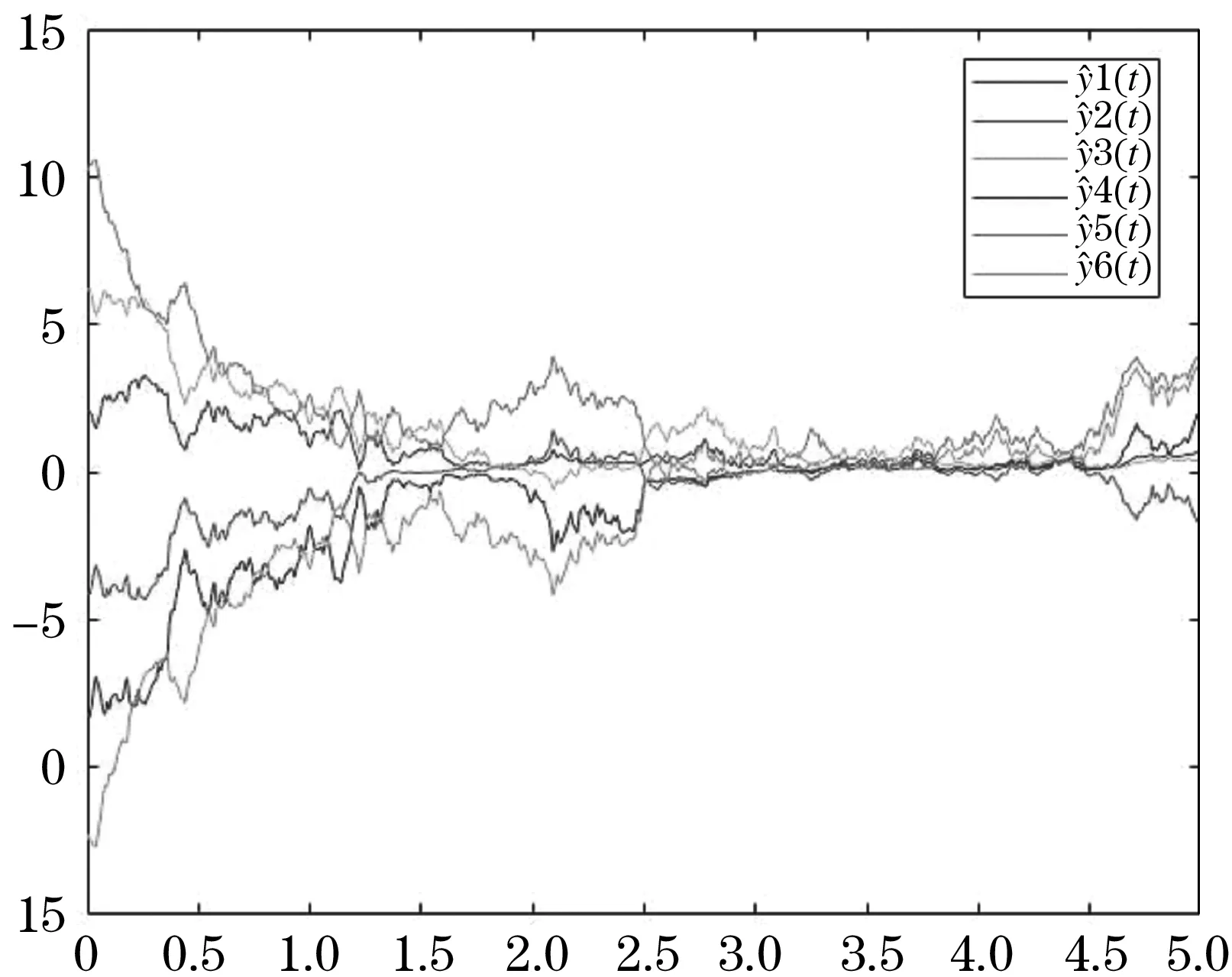
图4 响应系统层的轨迹Figure 4 Trajectory of the of the response system
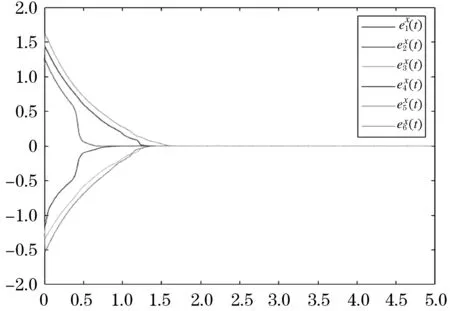
图5 误差系统ex的轨迹Figure 5 Trajectory of the ex-layer of the error system
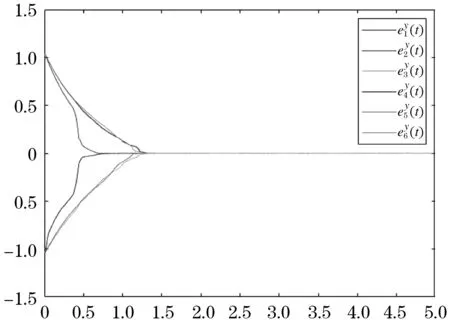
图6 误差系统ey的轨迹Figure 6 Trajectory of the ey-layer of the error system
4 结 语
本文首先构造了一个具有随机扰动和离散时滞的模糊BAM神经网络模型,进而设计了合适的反馈控制器,使得驱动系统和响应系统达到了固定时间同步.最后进行了数值模拟验证了理论结果的有效性.

