混合灰色预测模型HGM(1,1)
适越通,秦华,白成昊,刘子祥
(山东理工大学 物理与光电工程学院,山东 淄博 255049)
灰色理论首先由邓聚龙教授[1]提出,国际上给予了很高的评价。灰色系统为部分清楚、部分未知的数据信息[2-5],此理论认为尽管信息复杂、朦胧,但有一定的发展趋势和整体功能。本文研究分析了GM(1,1)[1]、基于缓冲算子和时间响应函数优化的GM(1,1)[2]、VWGM、FGM(1,1)[3]等理论有关的诸多模型,发现它们存在的不足之处,并采用FGM(1,1)和VWGM的混合模型即HGM(1,1)对数据处理。混合的模型不仅将变权缓冲算子引入灰色模型,并且基于灰色关联分析和粒子群优化算法确定模型最优参数,不仅解决传统缓冲算子作用强度不可调的问题[6],还可能实现对原始数据的动态预处理,改善模型预测精度,保证预测结果尽可能地保持原有序列的内在趋势以及变化规律,提高模型拟合和预测的稳定性和综合性能。
1 传统GM(1,1)
灰色预测方法的特点:首先把离散数据看作连续曲线上的离散值,由于连续函数可微分,从而转变为微分方程处理这些数据;其次由原始数据产生累加生成数,对累加生成数使用微分方程模型,以便找到数据的规律性。灰色系统理论的微分方程模型为GM(1,1)[1],表示1阶的、1个变量的微分方程。
设有原始数据列X(0)为
X(0)={x(0)(1),x(0)(2),x(0)(3),…,x(0)(n)} ,
(1)
式中n为数据个数。根据X(0)数据列建立GM(1,1)来实现预测功能,得预测后数据为
(2)
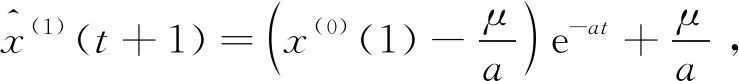
可得
(3)
式中:a为灰色发展系数;μ为灰色作用量。
2 首输入GM(1,1)
2.1 传统GM(1,1)原始数据列的首项x(0)(1)无效
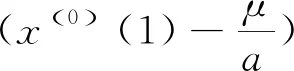
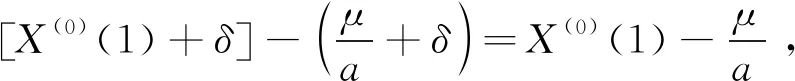
(4)
因此,由GM(1,1)得到的模拟值以及预测值,均与任意常数δ和原始数据列的首项无关。
2.2 FGM(1,1)建模方法
在原始数据首项前加入任意常数,以便获取原始数据列首项的信息。FGM(1,1)的具体建模方法如下:设原始序列为
X(0)={X(0)(0),X(0)(1),X(0)(2),…,X(0)(n)},
其中首项X(0)(0)为任意常数。由最小二乘法得
t=1,2,…,n。
这样原始数据的首项信息也被利用,原始数据的整体性不被破坏,FGM(1,1)预测得到的数据更加准确。
3 变权缓冲GM(1,1)
3.1 基于变权缓冲算子的数据预处理
传统缓冲算子是一恒量,缓冲效果不是过弱就是过强,因此对于数据预处理适应性不强。把缓冲算子进行变权弱化以及运用背景值优化对传统GM(1,1)进行改进[8],可实现对原始数据预处理动态化,增强数据适应性。设X=[x(1),x(2),…,x(n)]为原始数据列,有
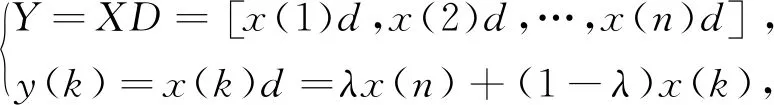
(5)
式中:0≤λ≤1;x(k)>0,k=1,2,…,n。当X为单调增、单调减或振荡序列时,称D为变权弱化缓冲算子,λ为变权缓冲系数。设原始数列为非负序列系统,r(k)表示数据序列X中从x(k)到x(n)的平均变化率,X经缓冲算子D作用后的数据序列为,XD=[x(1)d,x(2)d,…,x(n)d],则称
(6)
为缓冲算子D在k点的调节度[9]。缓冲算子D在各点调节度均为常数,且与变权缓冲系数相等,即δ(k)=λ。
3.2 变权缓冲GM(1,1)建模过程
构建变权缓冲GM(1,1)(VWGM)建模,使用变权缓冲算子D对原始数据预处理,并构造变权背景值Z(1)
(7)
式中η为背景值生成权重系数,0≤η≤1。通过最小二乘法求解,累减还原得预测值
(8)
上述模型是传统GM(1,1)的拓展,当λ和η取0.5时,模型退化为传统GM(1,1)。
3.3 基于灰色关联分析和粒子群优化算法的模型参数优化
为寻找最优λ和η值,用粒子群优化算法求解[10],可得到最优解。为确保预测结果最大限度保持原有数据内在变化规律,避免陷入局部最优,基于灰色关联分析,以拟合值与实际值的灰色关联度最大构建适应度函数。
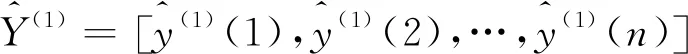
(9)
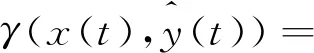
(10)
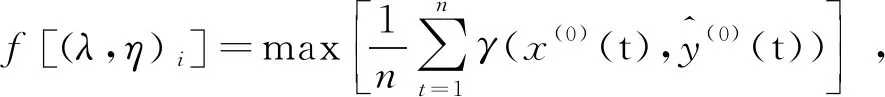
4 混合GM(1,1)
由以上论述知,FGM(1,1)以及VWGM各有其优点和其不足,经分析验证,其优缺点是可以互补的。将以上两模型整合得到混合GM(1,1)(HGM(1,1)),这就可以充分利用两者的优点,避免缺点影响预测结果。HGM(1,1)的具体建模步骤如下:
1)基于灰色关联分析和粒子群优化算法优化模型参数。
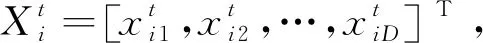
(11)
式中:t为粒子当前更新迭代次数;c1和c2为加速因子,均为常数;r1和r2为[0,1]区间的随机数;ω为惯性权重因子。粒子通过式(11)不断更新速度和位置,直到到达最大迭代次数或搜索到的位置满足预定适应度值时停止搜索;
2)利用FGM(1,1)对原始数据列处理,步骤如3.2中所述。
3)利用1)中求解的最优参数λ和η,对原始数据列进行预处理并求出预测。
(1)使用变权缓冲算子D对原始数据列预处理,弱化随机性增强趋势性,得处理后
(12)
(2)一次累加生成,将预处理后的数据进行累加得
(13)
(3)构造变权背景值Z(1)
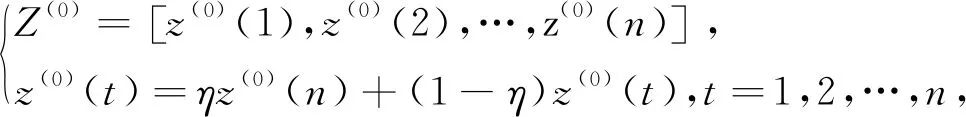
(14)
式中η为背景值生成权重系数,0≤η≤1。构建GM(1,1)模型y(0)(t)+az(1)(t)=μ式中a和μ为模型的灰色发展系数和灰色作用量,可通过最小二乘法求解,求得模型的解,累减还原得预测值
5 实例分析
为了检验分析HGM(1,1)模型在中长期预测中的有效性,用文献[11]中的数据对模型进行验证。以某地1998—2005年负荷数据为建模数据(表1),对2006—2008年的负荷进行预测。由表1可知建模负荷数据既有逐年增长的趋势,也有不确定的波动。分别使用4种模型建模预测,拟合结果见表1,预测结果见表2。
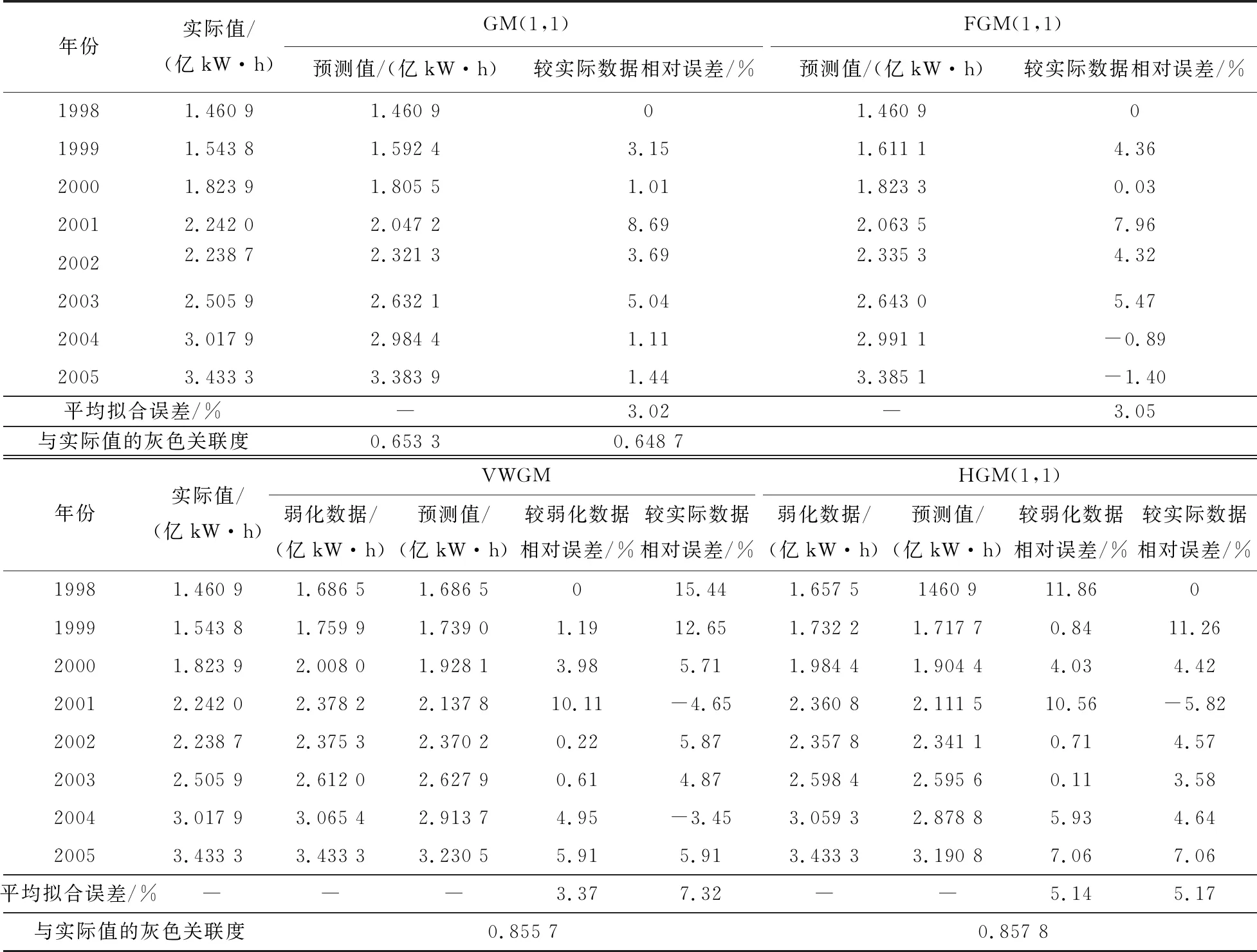
表1 四种模型的拟合结果

表2 四种模型的预测结果
模型1为传统GM(1,1),平均模拟相对误差为3.02%,拟合效果不错,但没有把握和弱化原始数据的波动性,平均预测相对误差达到了12.43%,预测效果不好。
模型2为改进模型FGM(1,1),平均模拟相对误差为3.05%,拟合效果也不错,但是平均预测相对误差达到了12.04%,较传统GM(1,1)有所改进,预测效果仍不好,但它有充分利用原始数据列的优点。
模型3 用粒子群优化算法选择最优的变权缓冲系数,粒子群算法基本参数设置为:种群规模m=30,最大迭代次数tmax=2 000,c1=c2=2,ωmax=0.9,ωmin=0.4,寻得模型最优参数为λ=0.1144,η=0.756 7。拟合值较实际值的平均拟合相对误差为7.32%,灰色关联度为0.855 7,平均预测相对误差为3.38%,拟合与预测效果较稳定,对于中长期预测精度较高。
模型4 仍采用模型3运用的粒子群优化算法选择最优的变权缓冲系数,粒子群优化算法基本参数设置相同,寻得模型最优参数为λ=0.099 7,η=0.754 6。然后与模型2进行整合优化,形成混合HGM(1,1)模型,由表可知,拟合值较实际值的平均拟合相对误差仅为5.17%,灰色关联度为0.857 8,平均预测相对误差仅为2.93%。拟合与预测效果较以上模型均更加较稳定可靠,与以上所有模型相比,无论在实际值拟合误差,预测值拟合误差,平均拟合误差,灰色关联度等等性能指标均优于以上所有模型,非常适用于中长期预测,性能改进明显。
6 结束语
提出的模型引入粒子群优化算法、变权缓冲算子以及FGM(1,1)模型,先对原始数据进行动态预处理,再通过变权缓冲系数对算子作用强度实现微调,这样就有效解决了传统缓冲算子作用强度不可调、缓冲效果过强或过弱的问题,以及忽略首项原始数据信息造成的信息不完整等问题,增强了模型的适应性,充分利用原始数据信息,提高模型的预测精度,实用性很强。
其次,提出的模型以拟合值与实际值的灰色关联度最大为目标进行参数优选,运用灰色关联分析和粒子群优化算法,充分运用所有原始数据信息,最大程度地保持了原始数据的内在变化规律,实现了数据预处理与原有预测问题的有机统一,模型拟合与预测效果均更加稳定可靠。模型可以运用到环境管理、资源管理、城市规划等实际生活当中。

