Reliability Evaluation of All-User Terminals in LEO Satellite Communication Network Based on Modular Reduction

Yangyang Du,Sifeng Liu,Zhigeng Fang,Su Gao

1 College of Economics and Management,Nanjing University of Aeronautics&Astronautics,Nanjing 211106,Jiangsu Province,China

2 Institute of Telecommunication Satellite China Academy of Space Technology(CAST),Beijing 100094,China

Abstract: LEO satellite communication network has a large number of satellites distributed in low orbits,which leads to multiple coverage of many areas on the ground.It is hard work to describe and evaluate the reliability of LEO satellite communication network.To solve this problem,the reliability of all-user terminals in LEO satellite communication network is defined,and the corresponding reliability evaluation method is proposed in the paper.Due to the large scale of the interstellar network, a modular reduction algorithm using the modular network instead of the original network for state decomposition is proposed in this paper.Case study shows that the calculation time of the proposed method is equivalent to 6.28% of the original state space decomposition algorithm.On this basis,the reliability of LEO satellite communication network is further analyzed.It is found that the reliability of LEO satellite network was more sensitive to the reliability of Inter-Satellite link and the satisfaction of global coverage in the early stage,and it is more sensitive to the reliability of the satellite in the later stage.The satellite-ground link has a relatively constant impact on of LEO satellite network.

Keywords: reliability evaluation; LEO satellite communication network;modular approach;full probability formula;all-user terminals

I.INTRODUCTION

The LEO satellite communication network is a realtime system composed of multiple small satellites flying on the 200-2000km LEO plane.These small satellites have the advantages of simple fabrication,low cost and mass production.Additionally, the network has more diverse track, wider coverage, higher space-time resolution and synchronous precision compared with MEO and GEO satellite communication networks.Therefore, it shows incomparable superiority and application prospect in natural disasters,remote areas, civil aviation, offshore operations and other scenarios.

At this stage,a number of large-scale LEO satellite communication networks have been proposed in the world, such as StarLink, Iridium Next and OneWeb.Among them, StarLink of SpaceX launched two test stars.Microsat2-A/B formed a constellation system of 12000 tiny satellites on February 2, 2018.Iridium Next successfully completed the last set of satellite launches on January 11,2019,and announced the completion of the constellation network and operation officially on February 6, 2019.The first six satellites from OneWeb were also successfully launched by the Soyuz ST-B/Fregat-MT carrier rocket on February 28,2019.All of these reflect the rapid development of LEO satellite network.

Reliability is an important indicator for evaluating the performance of LEO satellite communication network,reflecting the ability of LEO satellite communication systems to provide users with the services they need.On one hand,reliability evaluation can provide reference for the comparison and selection of LEO satellite communication systems.On the other hand,it can identify the weakness for improvement and provide reference for decision makers.

1.1 Related Work

Network reliability was firstly proposed by Lee C Y in 1955 for communication network[1].It considered node failures and link failures,and studied 2-terminal reliability,k-terminal reliability and full-terminal reliability [2].The classic network reliability model has two basic assumptions.The first assumption is that the link has only two states: normal and faulty.The other assumption is that link failures in the network are independent of each other.According to literature research,the reliability evaluation methods of the network mainly include disjoint product sum [3, 4],factorization algorithm[5,6],binary decision diagram[7], ordered binary decision diagram [8], delimiting methods [9], simulation algorithms [10], etc.Some new methods such as deletion and reduction[11]were also proposed to calculate network reliability.

Compared with network reliability, the research of satellite network reliability started later.At the beginning,it focused on the use of satellite in-orbit data and test data for research.The hot issues were the reliability modeling and the analysis of satellite’s key components and subsystems.Castet J F et al.used data from NASA to perform non-parametric analysis on the reliability of earth orbiting satellites, and studied the reliability of satellite subsystems, and identified the key subsystems which easily caused the failure of the whole system[12].Kumar B P et al.analyzed the different failure conditions of the satellite spherical active phased array antenna and carried out a fault-tolerant design [13].Yu B et al.used the Wiener process of time scale transformation to capture battery capacity decay to estimate the reliability of satellite lithiumion batteries at points and intervals [14].Wayer JK et al.found that the failure of the attitude control subsystem was very important for on-orbit operation,and the degradation and failure of the attitude control subsystem in the LEO system were more frequent, more difficult, and earlier than GEO [15].On this basis,Damircheli M et al.proposed the concept of Fault Assessment Logic Model, using simulation methods to analyze the reliability of the low-Earth orbit flexible spacecraft attitude control subsystem[16].In addition,some scholars conducted research on the reliability of satellites at the entire satellite level.Wang Chan et al.established the reliability evaluation system of the ZDPS-2 satellite based on the test data[17].Guo J et al.used Bayesian/Markov chain Monte Carlo method to model satellite reliability based on on-orbit failure data[18].Engelen S et al.established Markov model and Monte Carlo analysis to analyze and compare the lifetime of nanosatellites and classic large satellites[19].

As the characteristics of satellite network become more prominent,the reliability of satellite network research tends to be at the constellation level.Ma J K et al.proposed a reliable satellite real-time data transmission scheme based on the RTP transmission protocol [20].He X studied the reliability of satellite communication systems from the perspective of survivability, and proposed a survivability evaluation method based on natural connectivity [21].Zhang J N et al.used the analysis method of probabilistic risk assessment,combined with network risk and fault tree theory, and proposed a satellite fault tree barbell risk model [22].Zhou S S et al.established the relationship model between constellation availability and satellite reliability from the perspective of the replacement mode of the backup satellite[23].Based on the link cost measurement and the established reliability model,Qing C et al.established the inter-satellite link reliability model[24].He S et al.considered the impact of mobility and dynamic environment, and improved the adaptive protocol to deal with the problem of time-varying channels in the air-to-ground link[25].Nie Y et al.used different types of queuing theory models to calculate LEO satellite network communication performance indicators,and then combined cost planning to construct the network utility function to evaluate the LEO satellite network’s survivability under natural failure conditions [26].Under the limitation of QoS indicators of different services,Cai R et al.derived a set of disjoint reliability road sets that meet the QoS constraints of the business to obtain network end-to-end reliability[27].

1.2 Contributions

However, these algorithms are not suitable to calculate the overall connectivity reliability of LEO satellite communication network.

Firstly, it can be observed that LEO satellite communication network has a three-dimensional complex structure which is different from the flat network.Satellite-Ground link (SGL) is too important in LEO satellite communication network to be ignored when considering the reliability.

Secondly, we need to pay special attention to the performance of the ground coverage using the satellite tool kit in LEO satellite communication network.Because the network only serves for the users in the coverage.To compute the overall connectivity of the network,we should consider about the coverage characteristics in the view of users.Besides, we should focus on the multiple coverage which exists in LEO satellite communication network.

Thirdly, the modularized method of the reliability of satellite interstellar communication network is proposed.The state of network modularization is simplified, and the state considered in the proposed method is only equivalent to 0.54%of the original state space decomposition.The calculation time is equivalent to 6.28% of the original State Space Decomposition algorithm and 3.18%of the KNR/KW algorithm.

This paper is composed of five parts which introduces the all-user terminals reliability to describe the performance of any two user terminals to communicate at any time.LEO satellite network needs to be transformed into network diagram on the basis of its structural in part II.And a series of models about the all-user terminals reliability of LEO satellite network considering the network connectivity and coverage are formed.The part III is about the interstellar network reduction,which turns the original large-scale network into the combination of smaller network.In this part,we should focus on the change of the new nodes and edges after the reduction.The next part is the case study which includes the algorithm comparison, reliability calculation and analysis of LEO satellite network.The last part is conclusion and future work.

II.RELIABILITY MODEL OF SATELLITE NETWORK

The basic structure of LEO satellite communication network includes space stations, ground stations and user station.The space station provides a connection between the network user and the gateway station.The ground station is mainly composed of a signal station,a network control center and a satellite control center.The user station is consisted of various user terminals.

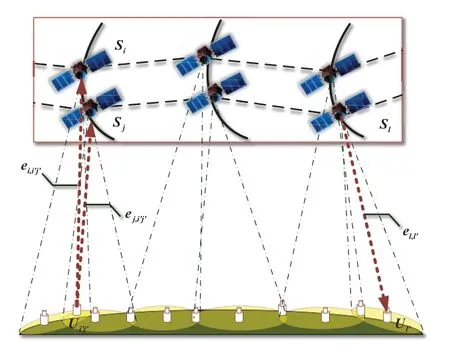
Figure 1. Schematic diagram of LEO satellite network structure.

2.1 Network Nodes and Links

This paper mainly studies the space-based LEO satellite network, without considering the links of the ground gateway station.Because in this mode, satellites are connected through Inter-Satellite link (ISL),and communication between terminals in the network can be realized directly without the support of ground gateway stations.According to the basic structure of LEO satellite network,the satellite network has an obvious three-dimensional structure, which consists of two parts.The first one is the interstellar network formed by regular connection between satellites, and the second one is the network formed by the interconnection between satellites and users in their coverage area.

It is assumed that the satellites and links in the LEO satellite communication network only have normal and failed states,and each part fails independently of others.

In the LEO satellite communication network,satellitemis abstracted into nodemof the graph, which are respectively recorded asS1,S2,...,Sm.The link between nodeSiandSjis denoted asei,j.The area only covered by the satelliteiis recorded as nodeUi′, and the area covered by the satelliteiand satellitejis nodeUi′j′, for the same reason, The area covered by the satellitei,j,...,lcan be recorded asUi′j′...l′.The link between nodeSiandUi′j′...l′is recorded asei,i′j′...l′.

So,the Interstellar network graphGI={S,EI},Sis the node set andEIis the edge set ofGI.And the network graphG={V,E},Vis the node set andEis the edge set ofG.

Among them, the quantity of areas covered by only one satellite isn1, the quantity of areas covered by only two satellites isn2,...,the quantity of areas covered by only m satellites isnm.

2.2 Network Connectivity and Reliability

In order to indicate the connection relationship between nodes, a reachability matrix is introduced to determine whether nodes can communicate with each other.

Definition 1.Adjacency matrix

Suppose G={V,E} is a simple graph, V={V1,V2,...,VN},N-order square matrix A(G)=[aij]is called the adjacency matrix of G.

Among them,

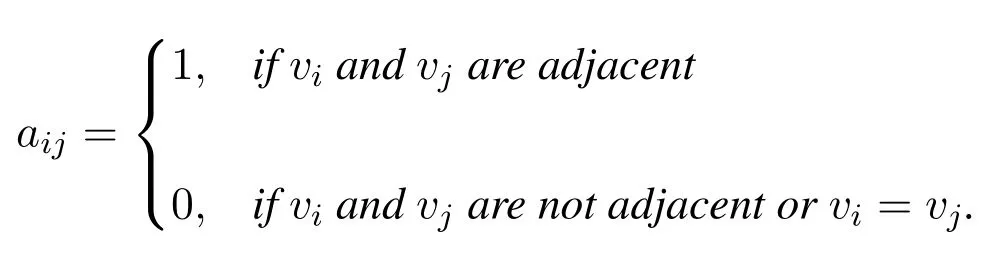
Theorem 1.Suppose S is a graph with n nodes{v1,v2,...,vn},and its adjacency matrix is A,then the(i,j)= (k=1,2,...)is thetotal number of paths whose length from node vi to node vj is equal to k.

Proof.Use mathematical induction onk.

Whenk=1,A1=A.From the definition ofA,the theorem is clearly established.

We suppose that the theorem 1 holds whenk=l,

Then whenk=l+1,

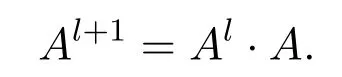
Therefore,

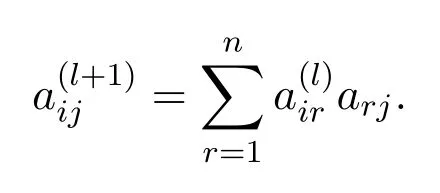
According to the definition of the adjacency matrix,arjis the number of roads with length 1 connectingviandvj,andis the number of roads with lengthlconnectingviandvr.Each item on the right side of the above formula means thatvipasses throughledges tovrandvrpasses through 1 edge tovj.Summing allr,which is the total number of paths with lengthl+1 fromvitovjcan be gotten.Therefore,the proposition holds forl+1.

Theorem 1 is proved.

Definition 2.Reachable matrix

The graph G={V,E}, V={V1,V2,...,VN}, the reachable matrix P of the graph G is N-order square matrix, and P= [pij]n∗n.If vi can reach vj directly,pij=1.Otherwise,pij=0.

The reachable matrix indicates whether there is a path between any two nodes in the graphGand whether there is a loop at any node.If there is a path between any two nodes, there must be a basic loop whose length does not exceed n,so the reachable matrixPcan be obtained from the adjacency matrixAofG.The method is to setP=A+A2+A3+...+An,change the non-zero elements to 1 and keep the zero elements remained inP.In this way,the resulting matrix is the reachable matrix[28].

Referring to the structure of the Iridium,each satellite is connected to the two satellites on the same orbit,the two nearest satellites on the left and right adjacent orbits,and the corresponding coverage user group.So the corresponding adjacency matrix can be obtained.

Select any node and edge in the graphG, and the combination of states where these nodes and edges exist or fail can be regarded as a state vector of onedimension space composed of such vectors.The combination is called state space, and all state space sets areT.

In the state space,each state vectortcan correspond to a specific state of the graphG, which is called sub graphG′.The set of nodes in the state space isVG′,where the set of nodes in the working state isVG′s,and the set of nodes in the failed state isVG′f.The set of edges in the state space isEG′,where the set of edges in the working state isEG′s,and the set of edges in the failed state isEG′f.

Since each sub graph contains invalid nodes and edges,in order to judge the connectivity of the graphs after these nodes and edges fail, the concept of sub graph connectivity probabilityR(TG′)is introduced.

Definition 3.If the sub graph G′ is capable of making all nodes in the graph G connected,R(TG′)is 1.Otherwise,R(TG′)is 0.

Assume that the reliability of the nodes areαvand the reliability of the edges areβe, then the reliability of sub graphG′

Therefore,the reliability of graphG

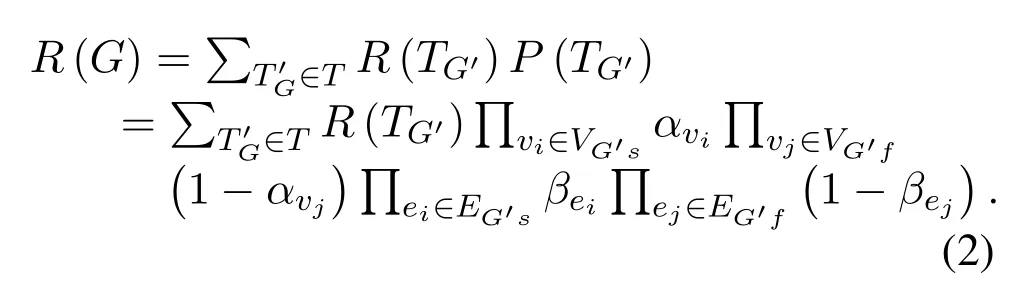
2.3 LEO Satellite Communication Networks Coverage

This part introduces the probability that the user group is covered by several satellites at the same time,to consider the situation of multiple coverage in the evaluation of the reliability of the communication of LEO satellite network.

The user groups are covered by satellites and recorded as an eventH.If only one satellite covers the user groups,it is recorded as One-coverageH1.If only two satellites cover the user groups,it is recorded as two-coverageH2.If onlyk(k ≤m)satellites cover the user groups, it is recorded ask-coverageHk, and so on.

One-coverageP(H1)= area covered by only one satellite/total service area

Two-coverageP(H2)= area covered by only two satellites/total service area

...

K-coverageP(Hk)= area covered by only k satellites/total service area

2.4 All-user Terminals Reliability of LEO Satellite Communication Network

Considering the connectivity and coverage of LEO satellite communication network, the concept of alluser terminals reliability is defined from the perspective of users.It is convenient for evaluating the ability of to make any two users communicate with each other at any time via LEO satellite network.

Definition 4.the reliability of all-user terminals

All-user terminals reliability means that the service area can be connected to each other at any two points.Since the users of LEO satellite communication network communicate with each other through the interstellar network,the reliability of the entire LEO satellite communication stereo structure can be simplified into that each user terminal can communicate with the interstellar network.In this way,every satellite has to be able to communicate with each other.

All-user terminals reliability of LEO satellite communication networks is recorded as eventB.Then,one-coverage of all-user terminals reliability can be recorded asB|H1,two-coverage of all-user terminals reliability can be recorded asB|H2,...,k-coverage of all-user terminals reliability can be recorded asB|Hk.

According to the full probability formula, all-user terminals reliability of the network

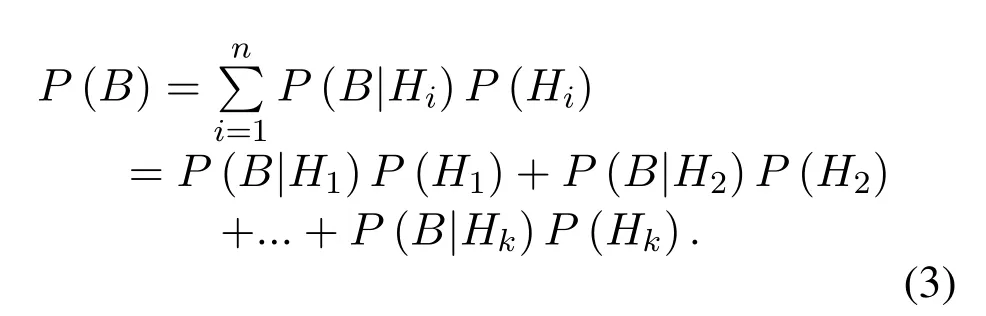
Among them, all-user terminals reliability of onecoverage

All-user terminals reliability of two-coverage

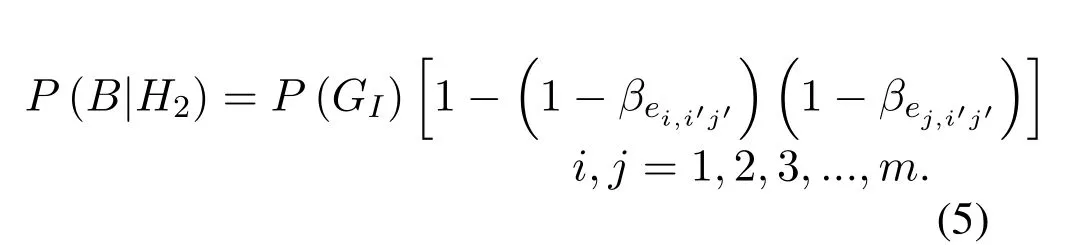
In the same way, all-user terminals reliability ofkcoverage

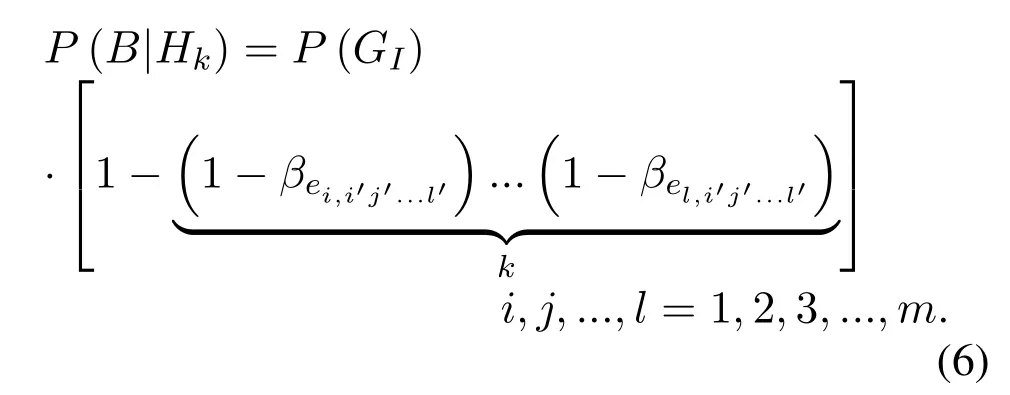
All-user terminals reliability of the Interstellar network which will be discussed in the next chapter is the most important part in these models.

III.INTERSTELLAR NETWORK REDUCTION

Due to the large number of satellites composed of LEO satellite communication networks, it is difficult to evaluate the reliability of large-scale network.This part proposes a method for evaluating the reliability of LEO satellite interstellar communication networks based on network modularization.

3.1 Interstellar Network Modularity

The structure of space-based LEO satellite communication network represented by iridium satellite is in the form of grid.This kind of network has a large number of similar structures.By dividing the large-scale network into multiple small network modules with similar structures,the evaluation can be simplified.

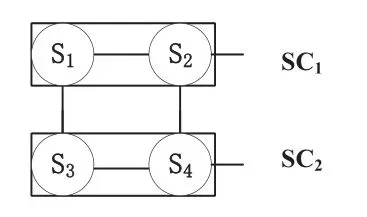
Figure 2. Four satellites modular.

If the Interstellar network is divided into some small network modulesSC1,SC2,...,SCw, the edge betweenSCrandSCtcan be recorded asecr,ct,r,t ∈ {1,2,..,w}.The spatial stateT1={SC1,SC2,...,SCw,ec1,c2,...,ecw−1,cw}is corresponded to the connected sub graph of the modular interstellar network graph.

So,the state space of the Interstellar network can be divided intoT1and its complementT1.

T=T1∪T1

={SC1,SC2,...,SCw,ec1,c2,...,ecw−1,cw}

∪{any one element is invalid in T1}

∪{any two elements are invalid in T1}

∪...

3.2 Reliability of the Network Modules

When the interstellar network is modularized, the reliability of the network modules should be recalculated.Each module of the network can be regarded as a small-scale network.The reliability of these modules can use the method above to evaluate.

The network module has the node set{sc1,sc2,...,sj}and the edge set{ec1,c2,ec2,c3,...,ecj−1,cj}.Find a connected sub graphand the corresponding state spaceTc0to evaluate the reliability.

For example, a 2*2 grid networkGI={s1,s2,s3,s4,e1,2,e1,3,e2,4,e3,4}is divided into two 2*1 modular networksSC1={s1,s2,e1,2}andSC2={s3,s4,e3,4}as Figure 2.

This resultp(SC1) =αs1αs2βe1,2andp(SC2) =αs3αs4βe3,4can be gotten.

3.3 Reliability of Links Between the Network Modules

The connection of the network has changed with the modularization of the network.The connection of the original network is between nodes, and the modular network is between modules.Therefore, the connection between nodes needs to be transformed into the connection between modules.

If regular modules are selected, there are certain rules between the modules because LEO satellite network has the shape of grid.The connection between modules can be regarded as the parallel structure of the inner node of the module and the inner node of the other module.This means that if three nodes in one module relate to three nodes in another module, the connection between the two modules is regarded as a parallel structure with three links.

About the network in Figure 2, the link between modular networksSC1andSC2is a parallel structure withe1,3ande2,4, so the reliability ofec1,c2is available.

βec1,c2=1−(1−e1,3)(1−e2,4)

3.4 Reliability of Interstellar Network

Combined with the above content,the network reduction is mainly through the following four steps:

a.Select the reduction module;

b.Recalculate the reliability of the module after the reduction;

c.Calculate the reliability of the edge between the modules after the reduction and combination;

d.Use the state decomposition method reduced modules.

According to the above steps,the network reliabilityR(GI)can be calculated.

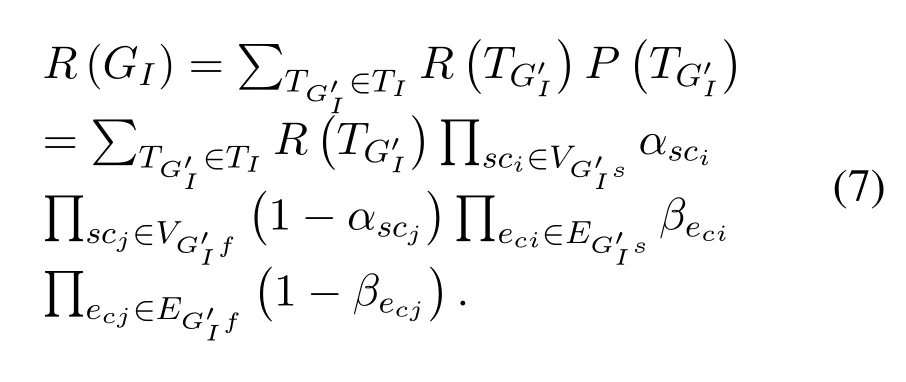
IV.CASE STUDY

4.1 Algorithm Comparison

For example,a 4*4 grid networkG1,as shown in the Figure 3, has 16 nodes and 24 edges.The reliability of the nodeSiisαi, and the reliability of the edge between nodesSiandSjisβi,j.

a.Select the reduction module.

Figure 3. 4*4 grid network G1.

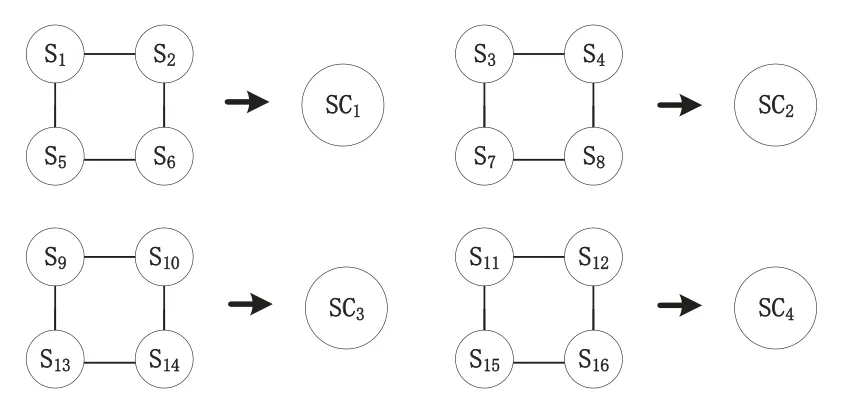
Figure 4. Modular process.

Node set{S1,S2,S5,S6}is reorganized intoSC1,{S3,S4,S7,S8}is reorganized intoSC2,{S9,S10,S13,S14}is reorganized intoSC3, and{S11,S12,S15,S16}is reorganized intoSC4.

Then,the original 4*4 grid network

can be reorganized to 2*2 grid networkGC1={SC1,SC2,SC3,SC4}.

b.Recalculate the reliability of the module after reduction.

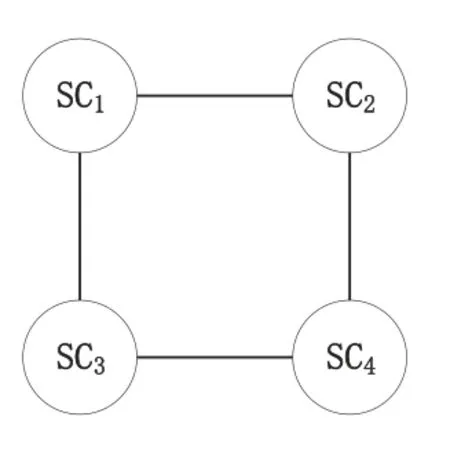
Figure 5. 2*2 grid network GC1 after modularization.

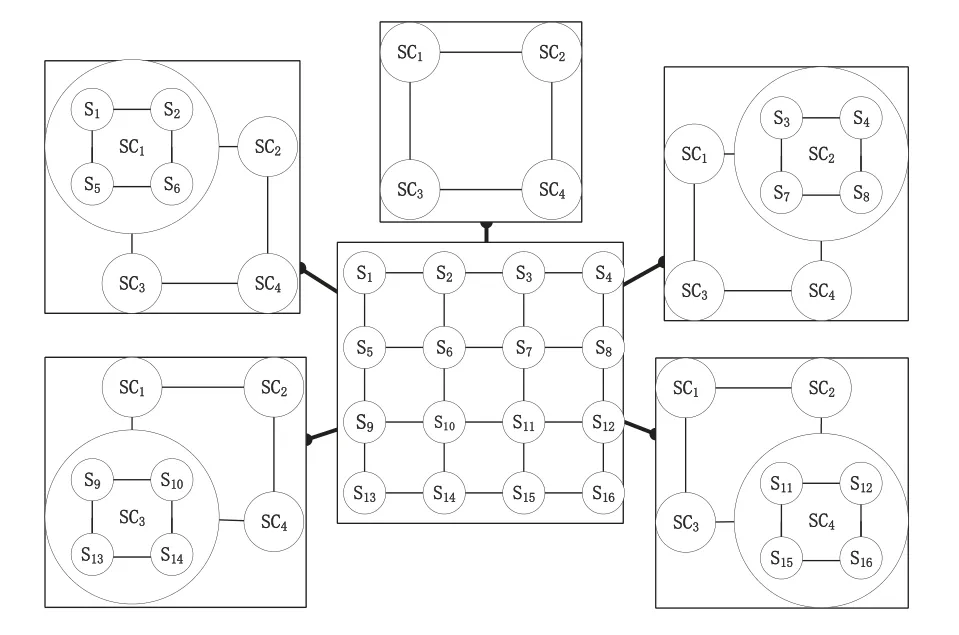
Figure 6. Schematic diagram of the original 4*4 network state decomposition.

c.Calculate the reliability of the edge between the modules after the reduction and combination.

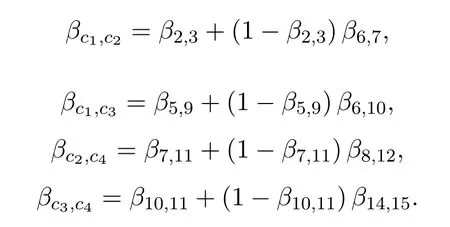
d.Use the state decomposition method reduced modules.

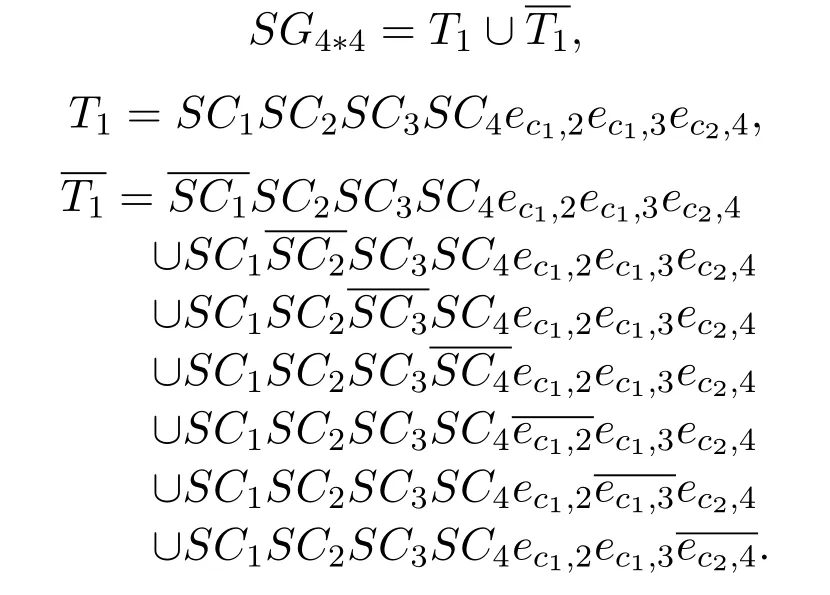
Assume thatαi=0.99 andβi,j=0.90,the reliability ofG1can be calculated andR(G1)=0.75142760.The network diagram should deal with 16777216 state vectors.After the state space decomposition, 203294 state vectors are processed.Compared with 737354 events of KNR/KW algorithm, the processing quantity is only 27.57%of that of KNR/KW algorithm[5].After the network modularization,only 1088 state vectors need to be processed, and the quantity is equivalent to 0.54% of that of only state space decomposition.Moreover,the operation speed of modular reduction method is 6.28%faster than the original network state space decomposition.

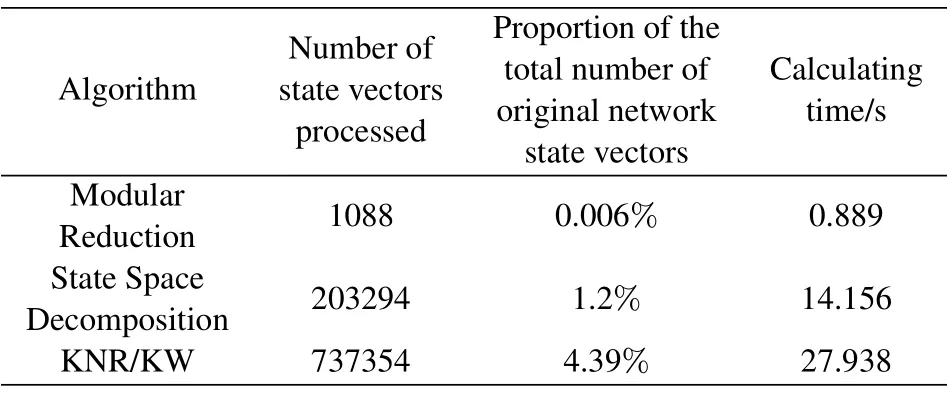
Table 1. Comparison of different algorithms.

Figure 7. LEO interstellar network structure.

4.2 Reliability Calculation of LEO Communication Satellite All-user Terminals

The LEO satellite communication network in Figure 7 consists of 72 satellites distributed on 6 near-polar orbits, and the cone half angle of each satellite sensor is 57.5 degrees.Each satellite has four inter-satellite links, which are respectively connected to two satellites in the same orbit and two satellites adjacent to the left and right orbits.

Similarly, calculate the reliability of the 6*12 grid networkGIaccording to the above method.

Assume thatαi= 0.996,βi,j= 0.98 andβi,i′...=0.85,

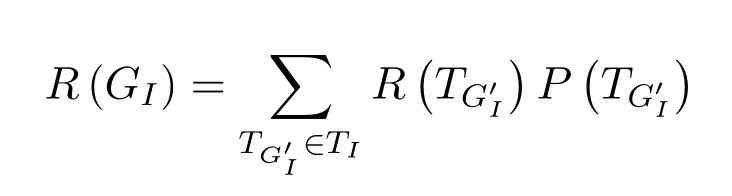
Figure 8. Coverage simulation of 72 satellites distributed on 6 near-polar orbits.

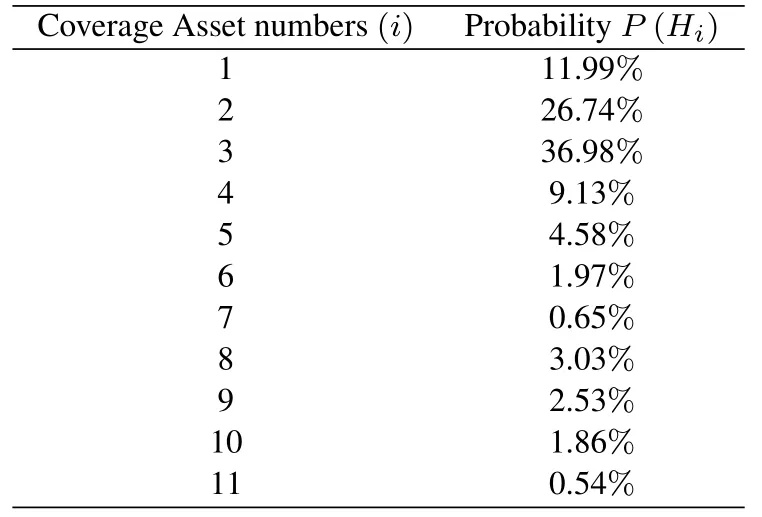
Table 2. The satisfaction of global coverage.

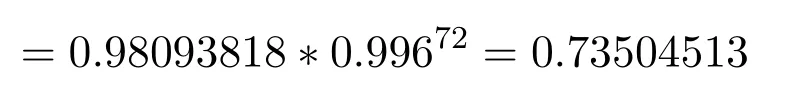
Then generate satellite coverage simulation map based on the coordinate information of the LEO satellite as Figure 8.Satellite Tool Kit is used to construct the LEO satellite network in this part,and the probability ofisatellites coverageP(Hi)can be obtained.

The results are shown in the Table 2.It can be seen the LEO satellite communication network exists 11-coverage.

Plug this into formula 6,we can get the results fromP(B|H1) toP(B|H11).And the all-user terminals reliability of the networkP(B)can be calculated according to the formula 3.

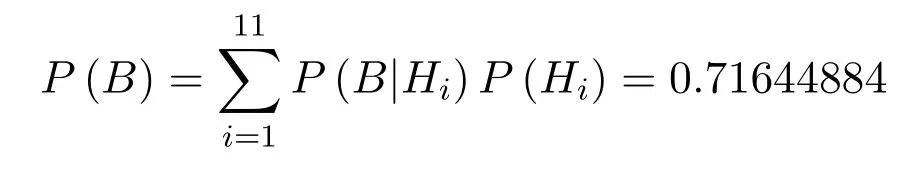
4.3 Reliability Analysis

Observe the LEO satellite communication network in Figure 7 running for 24 hours and sample the satisfaction of global coverage every minute.The reliability of all-user terminals of LEO satellite communication network is shown in Figure 9.It can be seen that the reliability curve fluctuates around 0.7165 in 24 hours,and the maximum difference does not exceed 0.004.The reliability of LEO satellite communication network is relatively stable.

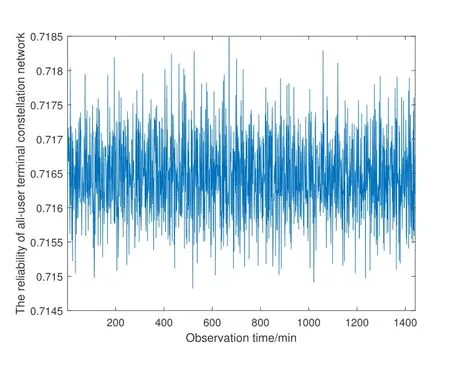
Figure 9. The reliability of all-user terminals in the LEO satellite communication network within 24 hours.

If LEO satellite network adopts different schemes,its all-user terminals reliability will be changed.Taking the LEO satellite communication network in Figure 7 as an example,the network is re-networked into 8 orbits, and 9 satellites in each orbit.The reliability of the re-networked LEO satellite communication network is shown in Figure 10.It can be observed from Figure 10 that the reliability of LEO satellite network after re-networking is relatively scattered, the central area of the reliability curve drops to 0.509, and the fluctuation of the reliability curve also increases 0.01.It can be clearly seen from the comparison that the 72-satellite network using 6 orbits has higher reliability and better stability than 8 orbits.

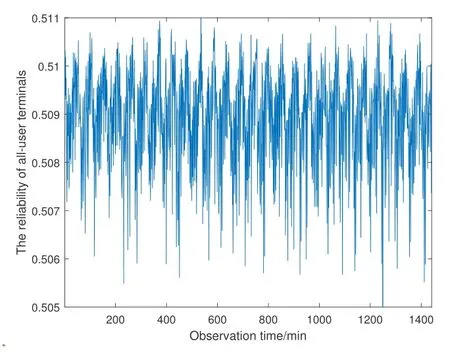
Figure 10. The reliability of all-user terminals in the renetworked LEO satellite communication network within 24 hours.

Not only does the satellite networking mode affect the reliability of LEO satellite communication network,the reliability of the satellite,ISL,SGL,and the satisfication of global coverage will also affect the reliability of LEO satellite network.These factors are analyzed below.

When the reliability of the links are constant,the reliability of all-user terminals in LEO satellite communication network shows an exponential increase trend with the increase of satellites reliability in Figure 11.At this stage, with the upgrading of satellite research technology,the reliability of satellites has been continuously strengthened, and it is very important to overcome difficulties and further guarantee the reliability of satellites in late period.

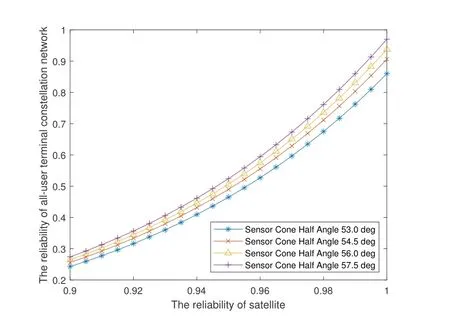
Figure 11. The influence of satellite reliability on the reliability of all-user terminals under different coverage.

This article mainly considers to the satisfication of global coverage by changing the cone half angle of the satellite sensor.The larger the cone half angle of the satellite sensor, the more the satellite covers, and the higher the reliability of the communication network is.When the reliability of the communication network is not high, the difference is not obvious.When the reliability of the satellite network increases to 0.96,if the cone half angle of the satellite sensor is increased,the reliability of the communication network will be significantly improved.

When the reliability of the satellites and SGL are constant, the reliability of all-user terminals in LEO satellite communication network changes with the reliability of ISL as shown in Figure 12.The increase in the reliability of ISL has led to a gradual increase in the reliability of satellite communication network,but the rate of increase has continued to slow down.When the reliability of ISL is greater than 0.94,the increase rate of the network reliability is significantly reduced.Therefore,improving the reliability of ISL in the early stage is the most meaningful for the reliability of the entire communication network.The influence of the satellite sensor on the network reliability is the same as the Figure 8.The network reliability is more sensitive to the cone half angle when the reliability of ISL is higher.

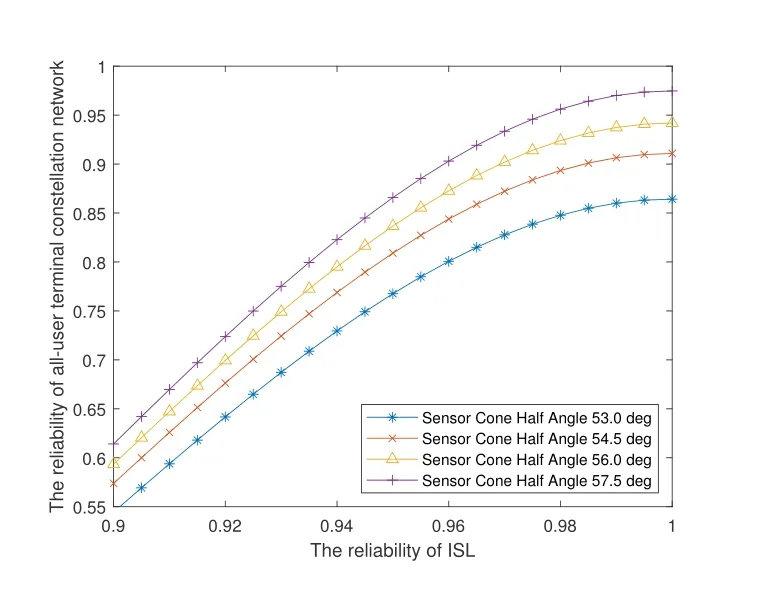
Figure 12. The influence of ISL reliability on the reliability of all-user terminals under different coverage.

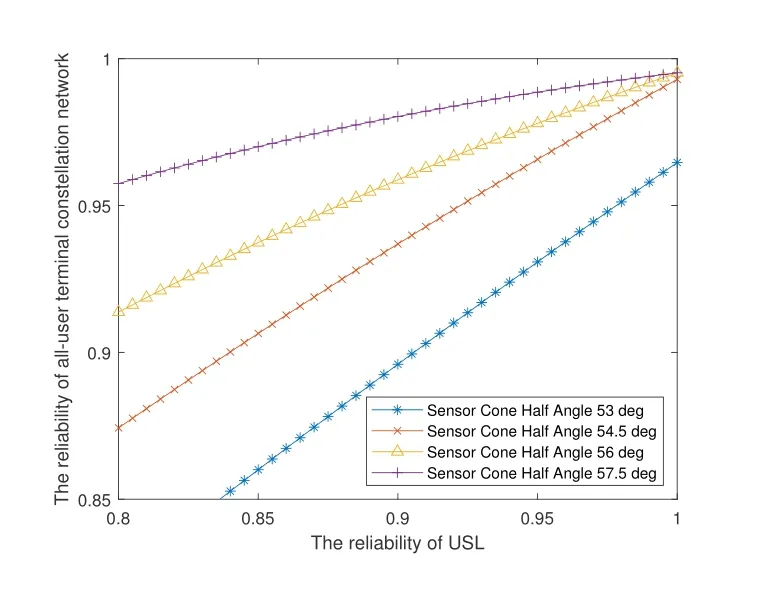
Figure 13.The influence of SGL reliability on the reliability of all-user terminals under different coverage.

When the reliability of satellite and ISL are constant,the increase in SGL reliability continues to promote the increase of the reliability of all-user terminals in LEO satellite communication networks in Figure 13.For SGL,since the propagation of radio waves needs to pass through the troposphere, stratosphere,ionosphere and outer space,there are many factors to affect the reliability of SGL, including multipath and shadow effects caused by ground obstacles[25].The reliability of SGL is lower than that of ISL.When the cone half angle of satellite sensor is 53 degrees, the communication network cannot guarantee full coverage of the world, and its reliability is lower than others.Therefore, the satellite parameter configuration should ensure that the cone half angle is greater than 53 degrees.The reliability of the communication network increases with the reliability of SGL at a relatively constant rate,so it is necessary to pay attention to the reliability of SGL throughout the stage.

V.CONCLUSION AND FUTURE WORK

This paper presents a method for calculating all-user terminals reliability of LEO satellite communication network.This method considers both the structure and the service function of LEO satellite communication network.At the same time, network modularity can effectively reduce the size of LEO satellite interstellar network.The comparison proves that this reduction has high accuracy and less computation,and it is suitable for large-scale LEO satellite communication network.The application of LEO satellite communication network consisted of 72 satellites proves the practical value of the method.And it can provide reference for the survivability evaluation of LEO satellite communication networks.Through reliability analysis,it is obvious that the reliability of ISL and the satisfaction of global coverage should be focused in the early stage, the satellite reliability should be focused in the later stage,and the reliability of SGL should be paid attention to throughout the stage.This is very important to get the key point for the reliability of LEO satellite communication networks.

About the future work,the dynamic changes of LEO satellite network should be considered instead of the static network.In the process of the continuous operation of LEO satellite communication network,the position of the satellite, the links between satellites and the overall connectivity of LEO satellite communication network changes dynamically.It is also possible to evaluate the service reliability of LEO satellite communication network considering the traffic,delay and so on.In addition, because LEO satellite communication network provides the communication service with the help of the MEO satellite network and the GEO satellite network,the combined reliability of LEO, MEO and GEO satellite networks can be considered in the actual work.

ACKNOWLEDGEMENT

This work was supported by the projects of the National Natural Science Foundation of China entitled“Reliability growth evaluation and prediction model of large aerospace (72071111)”, “Reverse multi variable CF-GERT model and its application for complex equipment development schedule under the background of multi project mixed batch(71801127)”and“Research on network of reliability growth of complex equipment under the background of collaborative development(71671091)”.It is also supported by a joint project of both the NSFC and the RS of the UK entitled “On grey dynamic scheduling model of complex product based on sensing information of internet of things”(71811530338).At the same time,the authors would like to acknowledge the partial support of the Fundamental Research Funds for the Central Universities of China(NC2019003,NP2019104),Postgraduate Research & Practice Innovation Program of Jiangsu Province(KYCX210239)and support of a project of Intelligence Introduction Base of the Ministry of Science and Technology(G20190010178).