Removal of Ocular Artifacts from Electroencephalo-Graph by Improving Variational Mode Decomposition

Miao Shi,Chao Wang,Wei Zhao,Xinshi Zhang,Ye Ye,Nenggang Xie,*

1 Department of Mechanical Engineering,Anhui University of Technology,Anhui,Ma’anshan 243002,PR China

2 College of Civil Engineering and Architecture,Anhui Polytechnic University,Anhui,Wuhu 241000,PR China

3 Department of Computer Science and Technology,Anhui University of Technology,Anhui,Ma’anshan 243002,PR China

4 Institute of Artificial Intelligence,Hefei Comprehensive National Science Center,Anhui,Hefei,230000,PR China

5 Department of Management science and Engineering,Anhui University of Technology,Anhui,Ma’anshan 243002,PR China

Abstract: Ocular artifacts in Electroencephalography(EEG)recordings lead to inaccurate results in signal analysis and process.Variational Mode Decomposition (VMD) is an adaptive and completely nonrecursive signal processing method.There are two parameters in VMD that have a great influence on the result of signal decomposition.Thus, this paper studies a signal decomposition by improving VMD based on squirrel search algorithm (SSA).It’s improved with abilities of global optimal guidance and opposition based learning.The original seasonal monitoring condition in SSA is modified.The feedback of whether the optimal solution is successfully updated is used to establish new seasonal monitoring conditions.Opposition-based learning is introduced to reposition the position of the population in this stage.It is applied to optimize the important parameters of VMD.GOSSA-VMD model is established to remove ocular artifacts from EEG recording.We have verified the effectiveness of our proposal in a public dataset compared with other methods.The proposed method improves the SNR of the dataset from-2.03 to 2.30.

Keywords: ocular artifact; variational mode decomposition; squirrel search algorithm; global guidance ability;opposition-based learning

I.INTRODUCTION

EEG recroding is the expression of electrophysiological activity of brain nerve cells in the cerebral cortex,which contains a lot of information[1].By decoding electrical signals in the brain, researchers build communication between the brain and external devices[2].EEG recording is a weak electrical signal, they are easily polluted by noise in the process of collection due to various factors such as environment,equipment and subjects themselves [3, 4].Ocular artifact is the most common disturbance in EEG recording.Removing ocular artifacts and extracting effective information from EEG recording are always important parts in EEG recording research.Many methods have been proposed to remove the ocular artifact from the EEG recording.At present,the main approaches of removing ocular artifact from EEG signal include independent component analysis(ICA)[5],wavelet transform(WT) [6] and empirical mode decomposition (EMD)[7].ICA does not work well for signals with a small number of channels.The WT has a good application in time series signal because of its characteristics in time domain and frequency domain.However the choice of wavelet basis can only rely on experience [8, 9].In addition,it is easy to generate modal aliasing in EMD[10].

At present, there are few researches on the application of VMD in EEG.VMD was proposed by Dragomiretskiyet al.[10] in 2014, which is a new adaptive signal decomposition method.VMD has great advantages in signal analysis and processing.It has no requirements on the number of channels,does not require the selection of a wavelet basis, and does not generate modal aliasing.VMD still has two parameters to determine, namely the number of decomposition modesKand the quadratic penalty factorα.Too large a value ofKleads to overdecomposition, and too small a value ofKleads to under-decomposition.Too large a penalty factorαwill narrow the bandwidth of the decomposed component of the orignal signal and vice versa.Improper setting of parameters results in under-decomposition or over-decomposition of VMD [11].Therefore, it is very important to optimize the parameters of VMD.Although researchers have made some discussions on the parameter selection of VMD in practical applications,most of them choose the trial-and-error method or the method of fixing one parameter to optimize another parameter.These methods either require a lot of computation time or ignore the coupling between the parameters.So there is still room for improvement.

In fact, the meta-heuristic intelligent optimization algorithm performs well in this kind of parameter optimization problem[12,13].The advantage of this kind of optimization algorithm is that they don’t need complicated formula derivation for the objective function,and have self-regulation on the search direction [14].Influenced by Darwinian evolution,Hollandet al.[15]first proposed genetic algorithm(GA)in 1975,which is a typical heuristic optimization algorithm.After GA was proposed,meta-heuristic optimization algorithms are like all flowers bloom together.Many researchers have come up with many different optimization algorithms to solve different practical problems.Lately,Mohit [16] proposed squirrel search algorithm(SSA)and this algorithm imitated dynamic foraging behavior of squirrels in southern forest.This paper proposed an improved squirrel search algorithm named GOSSA based on global optimal guidance and Oppositionbased learning,which is used to optimize VMD.

In this paper,GOSSA-VMD model is applied to decompose EEG recordings.First,GOSSA is used to optimize the parameters of VMD.Then the VMD model with the optimal parameters was used to decompose the EEG recording.The components related to the ocular artifact are filtered out by threshold method and then deleted, and the remaining components were reconstructed to get the processed signal.The method proposed in this paper can be applied to EEG recordings with few channels or even single channel.In addition, this method does not require additional eye electrical signals as a reference.The paper is organized as follow-section II mainly introduces the related work.In view of the part that can be further optimized in the squirrel search algorithm (SSA), an improved squirrel search algorithm named GOSSA is proposed in section III.In addition, it describes how to combine GOSSA and VMD.Section IV describes how to use this method to remove the ocular artifact.A practical example is used to illustrate the process of this method,and we test it’s performance in a dataset.Finally,Section V concludes the paper.

II.RELATED WORK

ICA is a kind of blind source separation, which can separate the source signals from the linear mixed signals of multiple source signals.ICA is based on mutual statistical independence between source signals,which does not require much prior knowledge and has better performance than traditional filtering.Mannanet al.[17] proposed a hybrid framework that combines ICA, regression and high-order statistics to identify and eliminate artifactual activities from EEG data.For improving the convergence speed and performance of ICA, Kimet al.[18] proposed a new ICA-AF method.The method combines ICA and adaptive filtering (AF), which can remove OAS in EEG without measuring EOG.WT is an effective tool for time-frequency analysis of signals.On the basis of the WT,researchers propose wavelet decomposition[19],wavelet packet decomposition[20],wavelet threshold[21] and other methods for signal analysis.Zikovet al.[22] used stationary WT to correct ocular artifact in EEG recordings.The advantage of this method is that there is no need to record the electroophthalmogram(EOG)signal itself.Venkataramananet al.[23]analyzed EEG recordings by haar wavelets of high orders.These ocular artifacts can be accurately detected by using the sharply discontinuous haar wavelets,thus completing the removal of ocular artifacts and accurate reconstruction of EEG signals can be achieved.EMD as part of Hilbert-Huang Transform(HHT)was proposed by Huanget al.[24]in 1998.EMD is widely used in time-frequency analysis of various signals,such as audio recordings [24], climate analysis [25]and biomedical signals [26, 27].Yanet al.[28] decomposed EEG recordings using EMD and screened components using threshold value to remove ocular artifact.

VMD has more advantages than other algorithms in overcoming modal aliasing and enhancing filtering effect.The core of VMD is to construct and solve a variational problem.Assuming that the original signalfis decomposed intoKeffective components.The decomposition sequence is guaranteed to be a modal component with a limited bandwidth of the central frequency, and the sum of estimated bandwidth of each modal component is minimized.The constraint condition is that the sum of all modes is equal to the original signal.The corresponding constraint variation expression is constructed as follows:

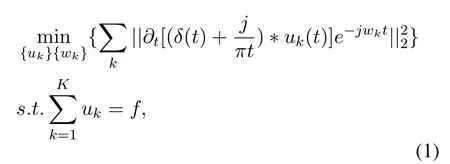
whereKis the number of modes decomposed,ukandwkare the corresponding kthmodal component and its center frequency, respectively.δ(t) is the real part ofuk,∗is the convolution operator.

The values of decomposition parameters are given in advance, which makes it difficult to achieve satisfactory analysis results.Many scholars have done some researches on these two parameters in some practical applications.Liuet al.[29] applied VMD to the time-frequency analysis of seismic timing signals.The optimal values ofKandαin this article are obtained through repeated experiments.The results show that the proposed method can effectively reduce the redundant component and improve the timefrequency representation of the components.Zhanget al.[30] used a parameter-adaptive VMD based on grasshopper optimization algorithm (GOA) to analyze vibration signals from rotating machinery.The weighted kurtosis index is defined as optimization objective function.Comparisons with the conventional fixed-parameter VMD method,this approach has more advantages.Xuet al.[31] improved VMD into a recursive mode algorithm based on the energy cutoff method.Particle swarm optimization(PSO)algorithm is used to take the optimal value of the penalty factor with bandwidth constraint ability to form the optimal recursive variational modal decomposition.Compared with the traditional VMD,the computational efficiency of this method has been greatly improved.

III.IMPROVED SQUIRREL SEARCH ALGORITHM AND ITS APPLICATION

3.1 Improved Squirrel Search Algorithm

3.1.1 Analysis of Squirrel search algorithm SSA has a simple structure and a high effectiveness.The initial location of the population was generated by using Eq.(2), wherepopmaxandpopminwere the upper and lower bounds of the search space respectively.FSi= [FSi1,FSi2,FSi3···FSin]was ann–dimensional vector, representing the position of the squirrel in then–dimensional search space.ndepended on real problems.U(0,1)was an uniform random number in the range[0,1].

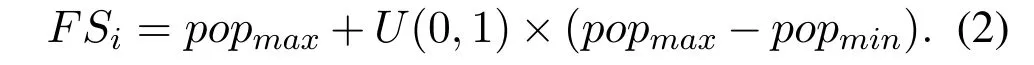
In SSA, the population is divided into three categories by ranking the fitness values of individuals.The position of squirrels was updated according to the following three cases:

Case 1.Squirrels on oak trees may move towards hickory trees:

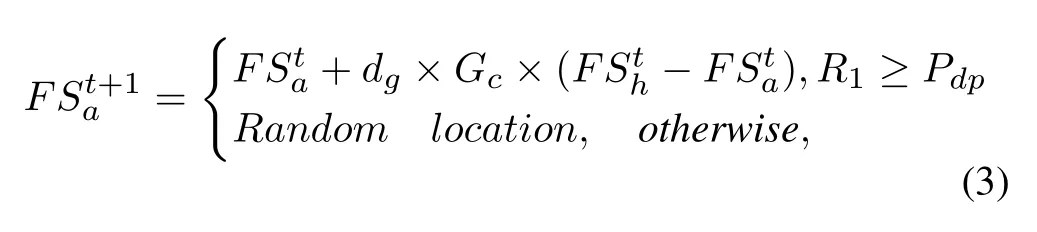
Case 2.Squirrels on normal trees may move towards oak trees:

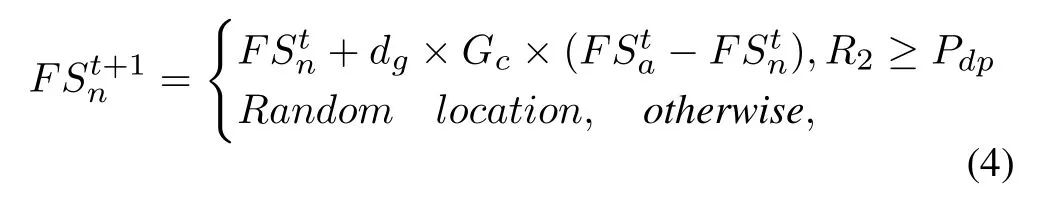
Case 3.Squirrels on normal trees may move towards hickory trees:

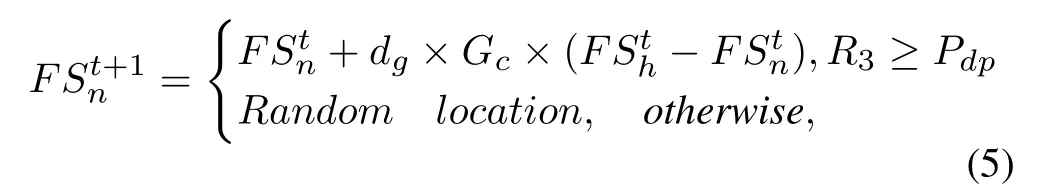
wherePdpis predator presence probability and its value is set to 0.1[16].R1,R2 andR3 are the random numbers in the range of [0,1].dgis random gliding distance of squirrel in forest.Generally, the general value ofdgis in the range of[9,20],but it is too large to interfere with results of the algorithm.Therefore,the value ofdgis scaled down to [0.5,1.1] by a scaling factor [16].FSh,FSa, andFSnare the position vectors of squirrels on the hickory tree, the oak tree and the normal tree respectively, andtrepresents the current iteration.Gcis a sliding constant and its value was considered as 1.9[16].

The category with better fitness affects the optimization direction of the category with inferior fitness.This multiple guidance method greatly increases the exploration ability of the algorithm, and makes the algorithm have a faster convergence speed.In order to avoid the algorithm falling into the local optimal solution, Mohitet al.[16] added the seasonal monitoring condition strategy into the algorithm and usedL´evyflight to reposition the individual position.It can be noticed from position updated formula, individual with optimal solution has great influence on the search direction of population.

In SSA, the current global optimal solution is generated by sorting the fitness values, which does not have the search ability.In this paper, the current optimal solution is disturbed during each iteration.The new current optimal solution generated by choosing the better one between the current optimal solution and the solution produced by perturbation.For enlarging the global guiding force of the optimal solution, the original seasonal monitoring conditions are improved.A counter is set in the algorithm.If the current iteration does not successfully update the current optimal solution, the count value of this counter is incremented by one.The condition is satisfied if the count value satisfies the threshold.Opposition-based learning is employed to relocate all squirrels except optimal solution in the population.Opposition-based learning was proposed by Tizhooshti [32], where the current candidate solution with its opposite individual was considered simultaneously to avoid immature convergence.Many scholars have used this method to the optimization algorithm and have achieved satisfactory results[33–35].Xiaet al.[36]solved the convergence and population diversity of PSO by obtaining backward learning mechanism.Simultaneously,a satisfactory performance on high-dimensional function was obtained.Donget al.[37] proposed a reverse learning particle swarm optimization algorithm based on niching technology.Better search efficiency and convergence speed on verification of trial functions than other algorithms were demenstrated.

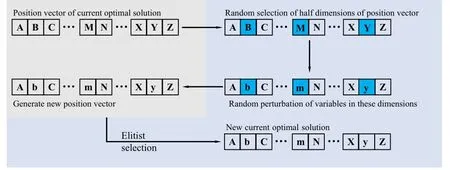
Figure 1. The perturbation process of the current optimal solution.

3.1.2 Disturbance optimal solution

In SSA,The current optimal solution didn’t participate in the population search process.It was in a passive state during the population update process.The current optimal solution was randomly perturbed once in each population renewal process.It can carry out an active local search.Sometimes it is easier to find a better solution near the current optimal solution.The perturbation process of the current optimal solution is shown in the figure.1.First,half of the dimensions in the position vector of the current optimal solution are randomly selected.Then, the values of variables on these selected dimensions are disturbed, the method of disturbance is shown as Eq.(6).Where (FSh)jis thej-thvariable of the current optimal solution.(popmax)j, (popmin)jrepresents the maximum and minimum of thej-thdimension of the search space.Finally, between the original current optimal solution and the new solution generated by perturbing the current optimal solution,a new optimal solution with better fitness is selected as the new optimal solution.

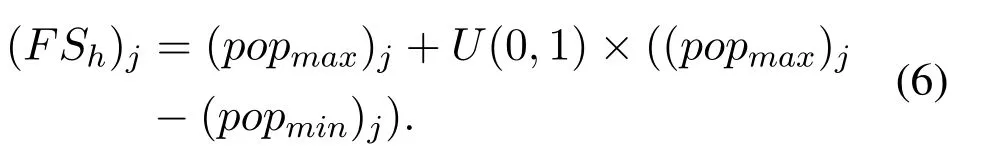
3.1.3 Feedback of updating the current optimal solution

In this paper,two-dimensional search space is taken as an example to analyze the individual update of SSA.It can be seen from Eqs.(3)to(5)that the three renewal formulas are similar.Taking the case 3 as an example,the process of individual update is shown in figure.2.

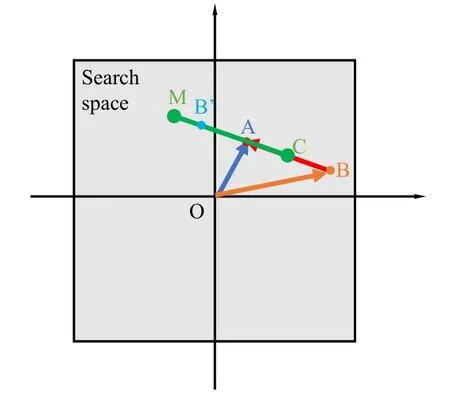
Figure 2.Schematic diagram of the position update formula for the case 3.

We assumed that pointAis the position of the current optimal solution),and pointBis the normal solution(According to the Eq.(5),pointB′on lineisIn the process of updating population position,pointBwill gradually approach pointA.The current optimal solution can guide the updating of the suboptimal solution and the general solution.When the current optimal solution is not updated in a certain period of time,the population will quickly converge to its vicinity.In intelligent optimization algorithms, there are two situations if optimal solution continually stagnates at the same value: 1) The algorithm has achieved the optimal solution.2)The algorithm has being trapped in local optimal solution.The optimal solution will not change under any circumstance, if it is in the former possibility.For the latter,a method is needed to help the population jump out of the local optimal solution.Seasonal monitoring condition is improved and the way of relocating squirrels in the end of winter by using opposition-based learning.In this paper,we compare the optimal value with that of the previous time after each update.If the optimal value does not change, we will count the number of unchanged times.

If the count value meets the threshold,then the positions of all squirrels are relocated by using oppositionbased learning except squirrels with the current optimal solution.Opposition-based learning was proposed by Tizhooshti [32], where the current candidate solution with its opposite individual was considered simultaneously to avoid immature convergence.Opposition-based learning can effectively help the algorithm jump out of the local optimal solution, the calculation is shown in Eq.(7) and Eq.(8), whereFShrepresents the current optimal solution,andrepresent the current candidate solutions.andare new locations produced by equations.Pseudo-code for improve seasonal monitoring conditions is in Algorithm1.Fitarrayis history optimization solution,tdenotes the value of current iteration.

Algorithm 1. Pseudo-code for improve seasonal monitoring conditions.1: if Fitt+1array ==Fittarray then 2: count=count+1 3: Whether trigger season detection conditions to determine.4: else 5: count=0 6: Eliminate the last ten squirrel individuals and use opposition-based learning to generate new positions.7: end if

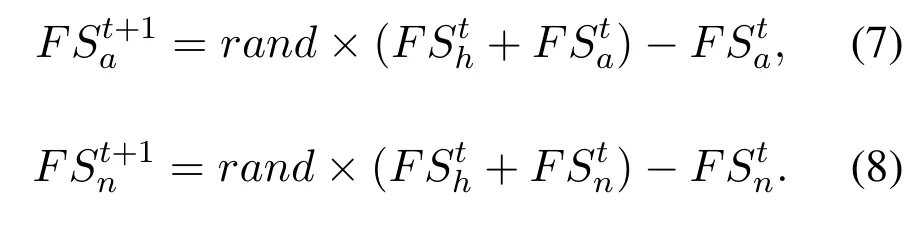
As shown in the figure.3, we assumed that pointArepresentsFSh,and pointBrepresentsFSaorFSn.PointB′′generated by Eqs.(7)and(8)falls randomly on lineEven if pointBconverges to the vicinity ofA,pointB′′still has a large search range.This method can help the algorithm to jump out of the local optimal solution effectively.The fitness of newly generated population is calculated and ranked and the population is divided into three subgroups.

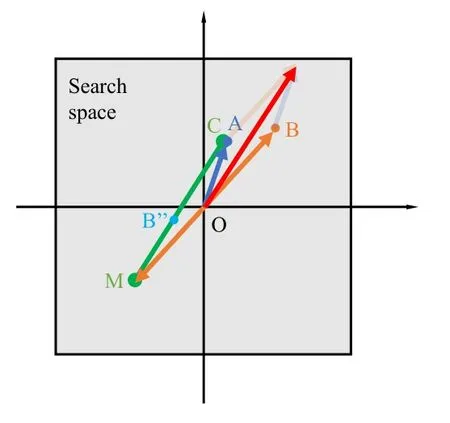
Figure 3.Schematic diagram of the position update formula(7)and(8).

If the current global optimal solution is continuously updated in the calculation process, it means that the seasonal detection conditions will not be triggered.In order to ensure the competitiveness of population in this case, the last 20% of the individuals will eliminated each time.Then,new individuals are generated by Eq.(8),which can directly enter the next generation population without calculating the fitness value.New individuals are added to the population to form the catfish effect,which makes the population more competitive.This strategy keeps the population diversity to some extent, and also enhances the global searching ability.Pseudocode for the improved algorithm is in Algorithm2.

3.2 Time Complexity

This paper analyzed the time complexity of the improved squirrel search algorithm (GOSSA).Population size, search dimension and maximum number of iterations are assumed to beN,dimandTrespectively.The time complexity is calculated in Eqs.(9)to (11), whereO1andO2are the time complexity of the squirrel routine search and the search that satisfies the seasonal detection conditions.The search times in these two cases areTaandTbrespectively,andTa+Tb=T.

Then she sat down on a stone, desired the young man to come near, and, giving him an affectionate kiss, she said, My long-hoped-for deliverer, kind heaven has led you to me, and has at length put an end to all my sufferings

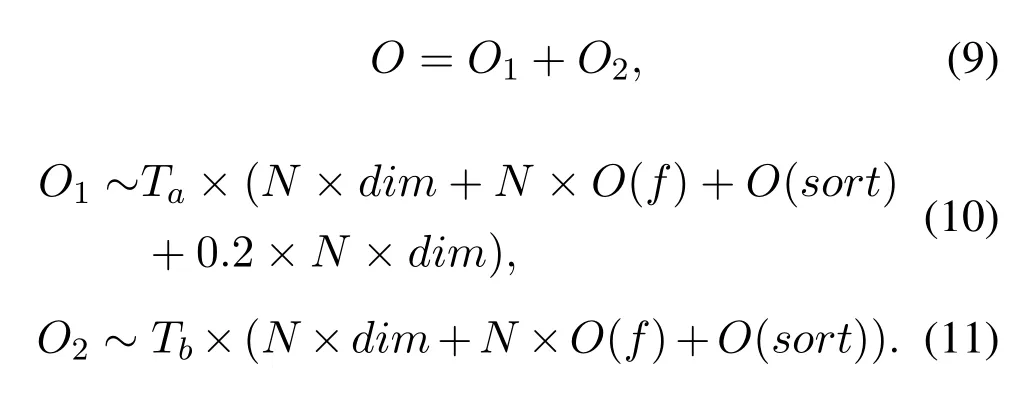
In Eq.(10),N×dimrepresents the time complexity of individual renewal in Eqs.(3)to(5)and Eq.(6).The time complexity for the operation of the last 20%of individuals in each replacement sorting is 0.2×N×dim.In Eq.(11),N×dimrepresents the time complexity of individual renewal in Eqs.(7)and(8).O(f)is the time complexity for the fitness calculation,and the specific value is determined by the objective function.O(sort)represents the sorting operation,and the specific value is N.To summarize, the final results is as Eq.(12).The time complexity of SSA is shown in Eq.(13).As shown in Eqs.(12) and (13), the time complexity of GOSSA is still on the same order of magnitude as that of SSA.The main time complexity of both depends on the time complexity of the fitness function, which isO(f).

Algorithm 2.Squirrel search algorithm based on opposition-based learning and global optimal guidance(GOSSA).Require: Iterations: tmax;Population: popsize;Dimension: dim;Ensure: the optimal solution;1: Set parameters and initial population location;2: Calculate the fitness of the population, and rank the initial population in increasing order according to fitness.According to the sorting,the population is divided into three groups.The first one is the optimal solution, the second to fourth is considered to be the suboptimal solution, the rest is considered a normal solution;3: for each i →tmax do 4: Update the squirrel position using Eqs.(3) to(5);5: The perturbation process of the current optimal solution;6: Repeat steps 2;7: if Fitt+1array ==Fittarray then 8: count=count+1 9: Whether trigger season detection conditions to determine.10: else 11: count=0 12: Eliminate the last ten squirrel individuals and use opposition-based learning to generate new positions.13: end if 14: end for 15: Determine whether the number of iterations is met.If the condition is met,end the iteration and output the current best position;16: The current best position is the final solution;

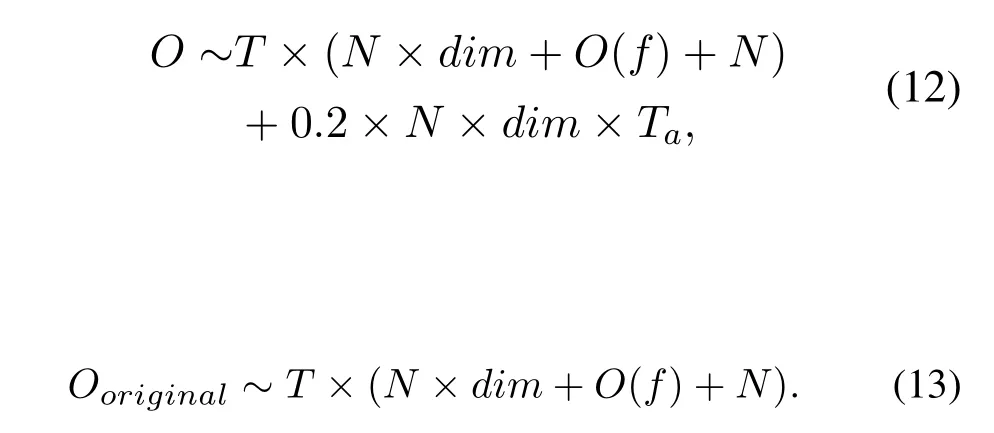
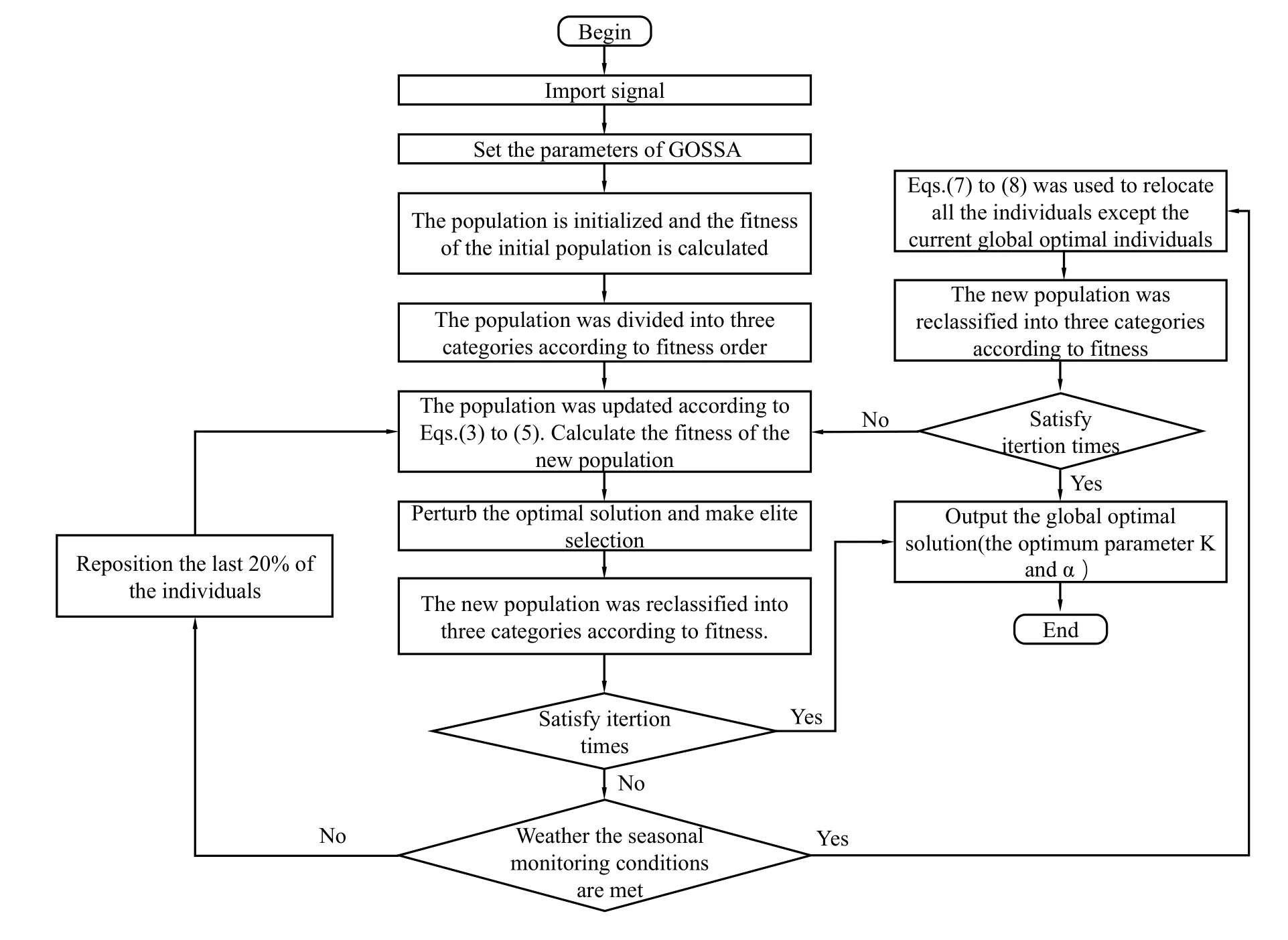
Figure 4. Flowchart of GOSSA-VMD.

3.3 GOSSA-VMD

It can be seen from VMD in Section 2 that the parametersKandαhas important influence on the algorithm performance.Therefore, choosing a reasonable set of parameters is the key to make the result of signal decomposition reasonable [38].The key of VMD based on GOSSA is the selection of the fitness function.Many scholars have studied this problem by using the cross-correlation coefficient [11, 38, 39] in Eq.(14), wherex(n) andy(n) are two sequences of lengthT.andrepresent the average values of the corresponding sequences.Crefers to the crosscorrelation coefficient betweenx(n)andy(n),which measures the similarity between them.

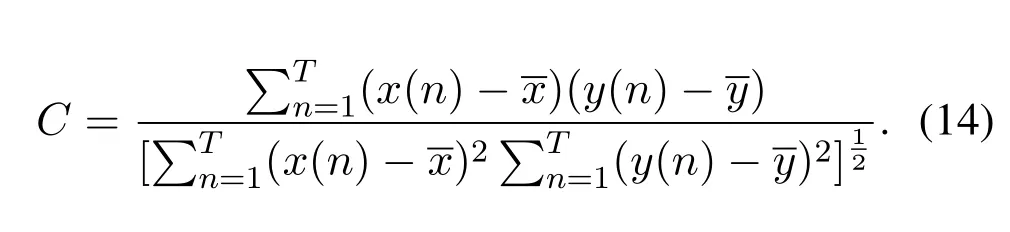
However, most scholars consider the crosscorrelation coefficient between the components and the original signal or the reconstructed signal(Sum of all components) and the original signal.In fact, the cross-correlation coefficient between the components is also noteworthy.Note that the distortion degree of the signal decomposed decrease with valueC.The correlation between the components is expected to be minimal while ensuring that the signal is decomposed without loss of truth.

This ensures that each component represents a different frequency band of the signal, which is conducive to the analysis of each component in the later stage.Therefore,the fitness function in this paper also considers valueCbetween each component after considering valueCbetween the reconstructed signal and the original signal.In addition, we perform spectral analysis of the signal.And the amplitude spectrum of the signal is used to replace the time sequence of the signal to calculate the cross-correlation coefficient.The fitness function proposed in this paper is shown as follows:

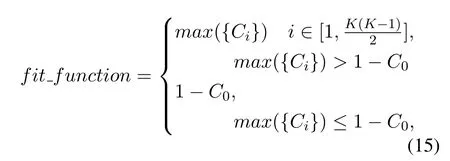
wheremax({Ci}) represents the set of crosscorrelation coefficients between the amplitude spectrum of components.Choosing two components fromkcomponents to calculate cross-correlation coefficient.The result is a set containingcrosscorrelation coefficients.C0refers to the crosscorrelation coefficient between the amplitude spectrum of reconstructed signal and the amplitude spectrum of original signal.The parameter combination that makesfitfunctionminimum is the optimal parameter combination.The flowchart of GOSSA-VMD is shown as figure.(4).

IV.GOSSA-VMD FOR REMOVAL OF OCULAR ARTIFACTS

The EEG recording is decomposed by GOSSA-VMD to obtain components.After each component is analyzed, The components of the ocular artifact were removed and the remaining components were reconstructed to obtain the EEG recording without ocular artifact.Normally, the ocular artifact has the characteristics of large amplitude.We conduct spectral analysis of the components obtained by signal decomposition and screen the components by using the difference between amplitude-frequency characteristics.Through analysis, it is found that the ocular artifacts components are mainly concentrated in the low-frequency components and the amplitude is obviously abnormal.This paper presents a threshold-based method to screen the effective components.The two metrics associated with the threshold are calculated as Eqs.(16) to (17), whereApsiis the largest value of each component.MApsis the average of the maximum values of all the components.

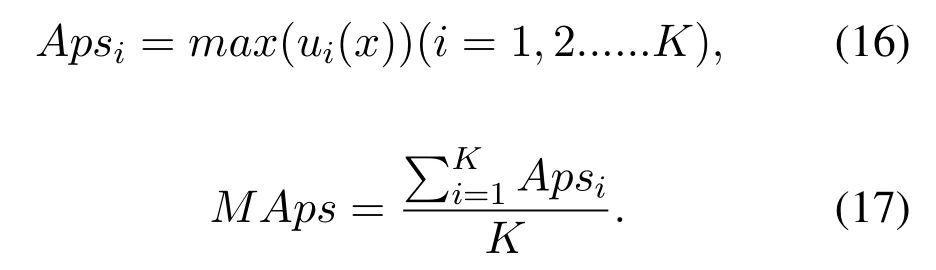
The threshold conditions are set as follows:

b) The central frequency of the component is less than 3Hz.

The flow chart of EEG recording removal the ocular artifacts based on GOSSA-VMD is shown in figure.5.

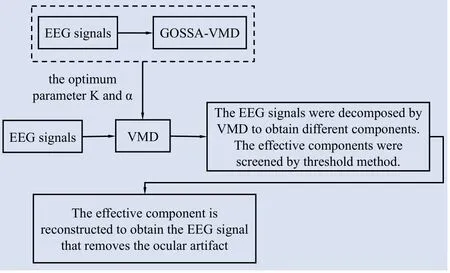
Figure 5. Technical route of GOSSA-VMD for removal of ocular artifacts.

4.1 A Case Study of GOSSA-VMD for Removal of Ocular Artifacts

In this section, the operation process of the method proposed in this paper is demonstrated through an EEG recording containing an ocular artifact.figure.6 shows the time-domain graph and amplitude spectrum of a pure EEG recording and the time-domain graph and amplitude spectrum of the signal mixed with ocular artifact.The population of GOSSA-VMD is set as 50, and the number of iterations is 15.The search range ofKandαis [2,20] and [20,10000], respectively.The optimal parameter is [15,9516].The results obtained by using the optimal parameters to decompose the signal are shown in figure.8.It can be seen from figure.8 that the maximum values of VMF1 and VMF2 are significantly larger than the other components.We analyze the spectrum of each component and draw spectrums in figure.9.In figure.9, the black line represents the amplitude spectrum of pure EEG recording, and the bule line represents the amplitude spectrum of the components resulting from the VMD.It can be seen from the figure.9 that the amplitude spectrum of VMF1 and VMF2 has almost no overlap with the amplitude spectrum of the pure EEG recording.

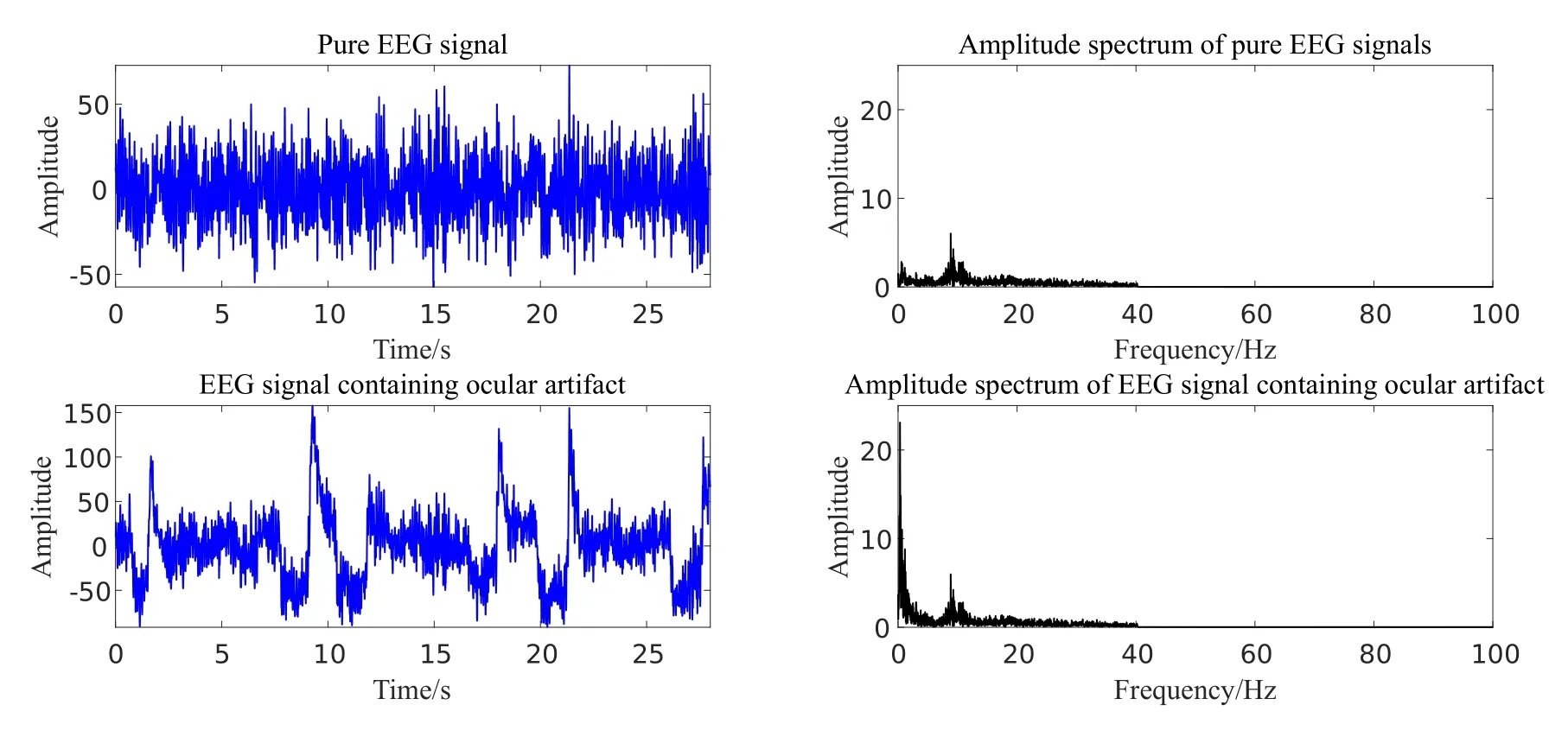
Figure 6. EEG recording and its containing ocular artifact.

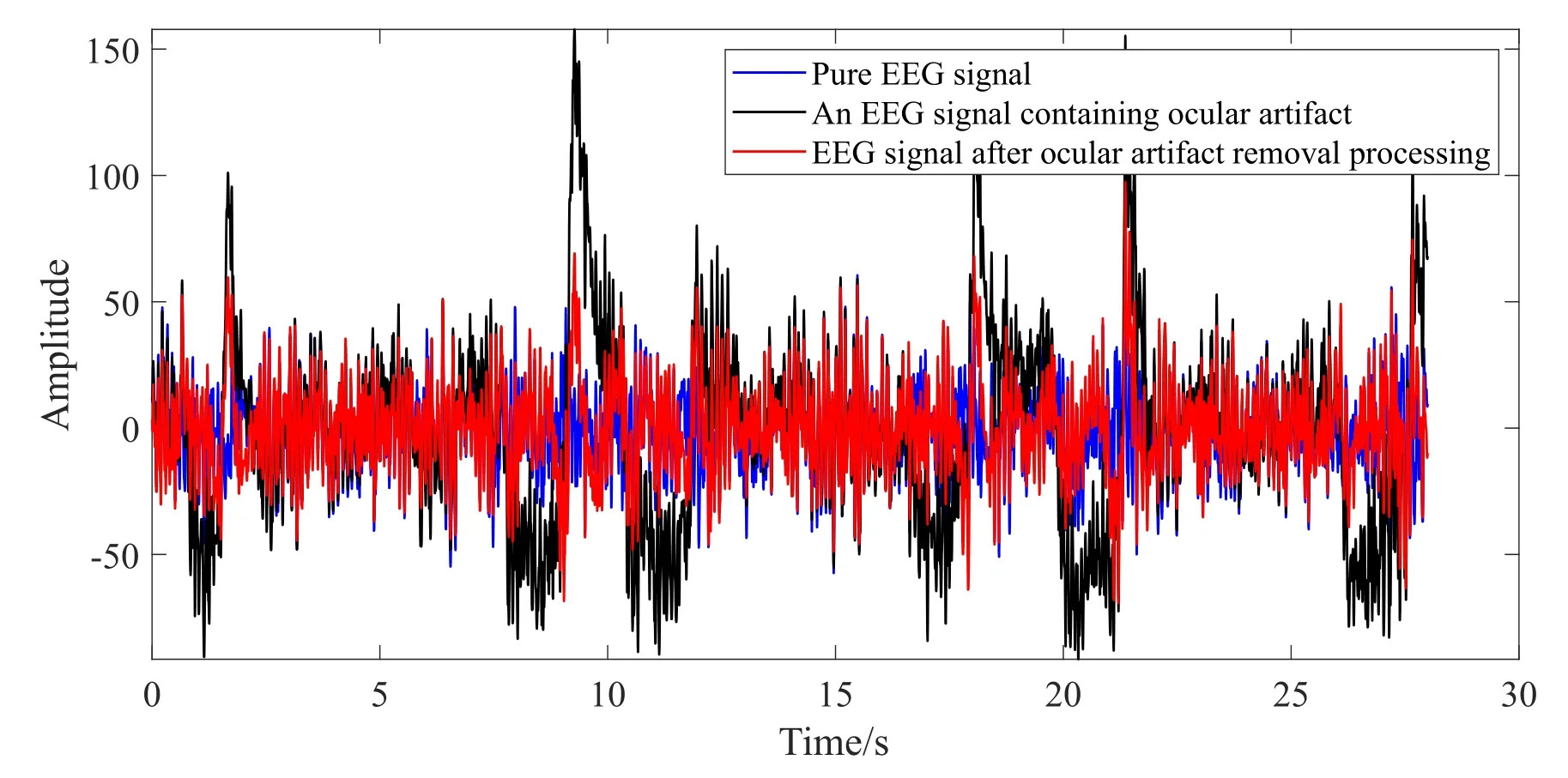
Figure 7. Time-domain graph of the EEG recording after the removal of the ocular artifact.

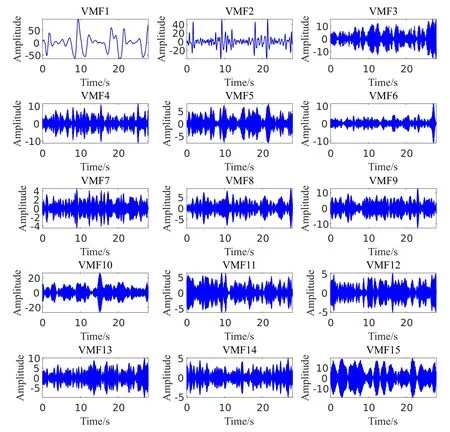
Figure 8. The result of signal decomposition.

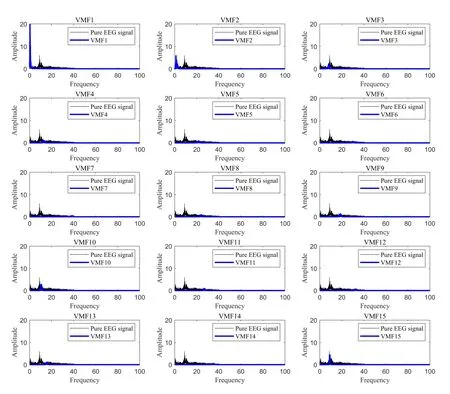
Figure 9. Amplitude spectrum of each component.

When a component satisfies both conditions a)and b), it is considered to be the component that mainly contains the ocular artifact.Signal-to-noise ratio(SNR)[40],root-mean-square error(RMSE)[41]and the cross-correlation coefficient were used to measure the removal effect of the ocular artifact.The calculation of these indicators is shown in Eqs.(18) to (19)and Eq.(14) respectively, wherexis the pure signal andyis the signal after processing.Nis the length of the signal.

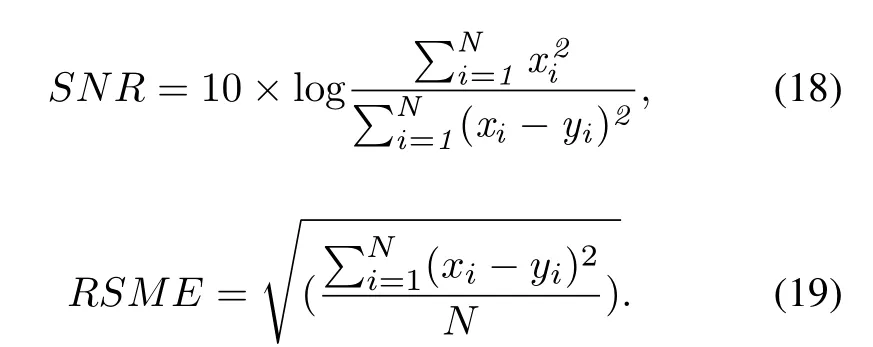
As present from Table.1,the method presented in this paper has a good effect in removing the ocular artifact.The final reconstructed signal is shown in figure.7.

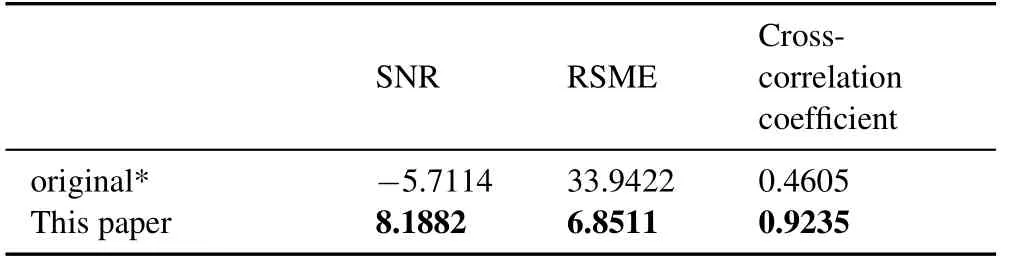
Table 1.Comparison of evaluation indexes before and after removal of eye electrical artifact.

4.2 Performance of GOSSA-VMD

We compare are proposal with other methods.FastIca is widely used for ocular artifact removal in EEG recordings.Castellanoset al.[42] proposed a novel wavelet enhanced ICA method(wICA).Advantage of wICA is its automation.These two methods are used to compare with the method proposed in this paper.

4.2.1 Dateset Description

Kladoset al.[43] presented a semi-simulated EEG dataset.This dataset used the model in [44] to mix ocular artifacts with artifact-free EEG.Because this dataset contains pure EEG recordings,it can be used to evaluate our algorithm.The EEG dataset was obtained from 27 healthy subjects, including 14 males and 13 females.19 EEG electrodes were used in the signal acquisition experiment, which were based on the 10-20 international system.The sampling frequency of the signal is 200Hz.All signals are filtered by band pass of 0.5-40Hz.In addition, the EOG signals were obtained from the same subjects.In order to obtain the semi-simulated EEG dataset, Kladoset al.[43] used the contamination model proposed by[44].

4.2.2 Results and Discussion

The first subject’s EEG recording is shown as a graphical example.figure.11 shows the pure EEG recordings of the first subject.figure.12 shows the EEG recordings mixed with ocular artifacts.It can be seen from figure.12 that the electrode channels closer to the eye is more seriously interfered by the ocular artifacts.This is in line with the channel distribution rule of the acquisition system in figure.10.These 6 channels are close to the eye, so it is reasonable that they are seriously disturbed by the ocular artifacts.These 6 channels were selected for ocular artifact removal.ICA and wICA[42]are used to compare the performance of the methods presented in this article.The mean value of SNR, RSME and the cross-correlation coefficient are used as evaluation indexes,and the resultes are shown in Table.2.It can be seen from Table.2 that our method is superior to ICA and wICA.It can be seen from figure.13 that the method proposed in this paper has good stability.Although the stability of SNR and Crosscorrelation coefficient is not the best, the overall results are better than ICA and wICA.

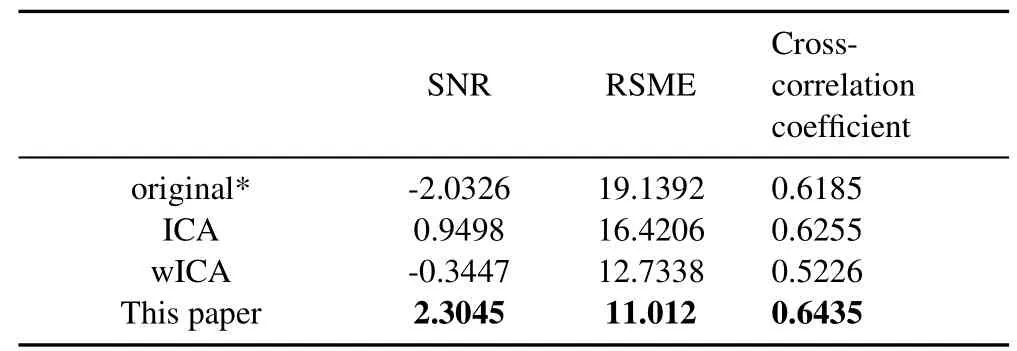
Table 2. An indicator of the EEG after the removal of the ocular artifact.

Figure 10. Brain conductance distribution.

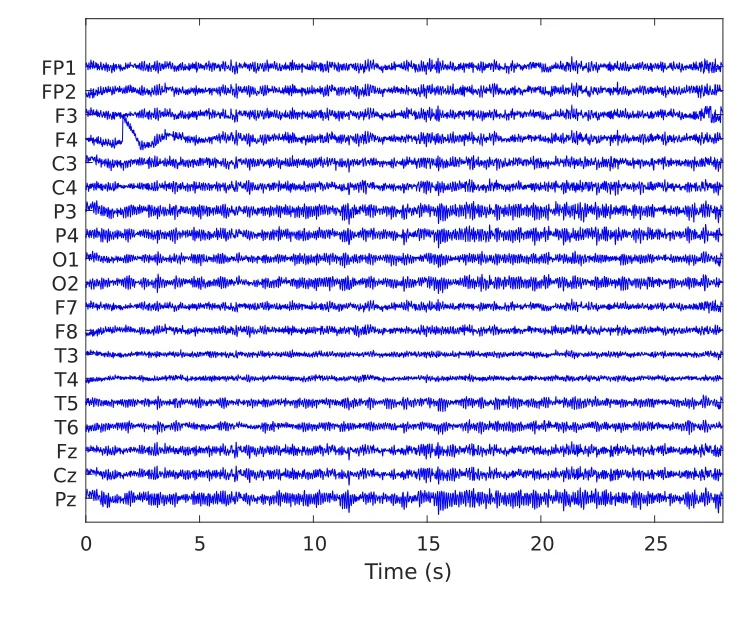
Figure 11. Pure EEG recordings.

Figure 13. A boxplot of the results for all subjects.

The most traditional ocular artifacts removal algorithms needs to record EOG itself, and then remove the ocular artifacts from the EEG signal through analysis and comparison.a series of methods based on ICA, require a large number of channels.Other WTbased methods need to choose a suitable wavelet basis,which requires a lot of prior knowledge.EMD does not require the number of channels, nor does it need to select wavelet bases, but the decomposed components are easy to produce modal aliasing.VMD has the advantages of EMD and overcomes the problem of modal aliasing between components.GOSSA is used to optimize VMD parameters, which enables the selection of VMD parameters to be adaptive rather than manual.From the analysis of the results,it can be seen that the method proposed in this paper can effectively remove ocular artifacts.

V.CONCLUSION

Aiming at the problem of removing ocular artifacts in EEG recordings,this paper proposes a GOSSA-VMD model.On the basis of the SSA, the influence of the current optimal solution in the iterative process is improved.In each iteration,the current optimal solution is mutated once, and elite selection is made between the new solution obtained by mutation and the current optimal solution.Feedback on whether the current optimal solution is successfully updated during each iteration is used to establish new seasonal monitoring conditions.Opposition-based learning is introduced into this stage for the relocation of individual positions.This method effectively prevents the algorithm from falling into the local optimal solution.We combine GOSSA and VMD for the removal of Ocular artifact.A fitness function based on the cross-correlation coefficient is introduced.After the signal is decomposed,the threshold method is used to filter out the components related to the ocular artifacts to achieve the removal of the ocular artifacts.The method GOSSAVMD proposed is effective for the removal of ocular artifacts.

There is still a part of the research content of this article worthy of further study.At present, with the development of brain-computer interface technology,the speed of EEG signal from signal acquisition to communication with external devices is required to be faster.How to improve the calculation speed of the method in this paper is also a question worthy of further consideration.

ACKNOWLEDGMENT

This work was supported in part by the Science and Technology Major Project of Anhui Province (Grant No.17030901037), in part by the Humanities and Social Science Fund of Ministry of Education of China(Grant No.19YJAZH098), in part by the Program for Synergy Innovation in the Anhui Higher Education Institutions of China (Grant Nos.GXXT-2020-012,GXXT-2021-044), in part by Science and Technology Planning Project of Wuhu City, Anhui Province,China(Grant No.2021jc1-2), and part by Research Start-Up Fund for Introducing Talents from Anhui Polytechnic University(Grant No.2021YQQ066).