Robust Trajectory and Communication Design for Angle-Constrained Multi-UAV Communications in the Presence of Jammers

Yufang Gao,Yang Wu,Zhichao Cui,Wendong Yang,*,Guojie Hu,Shiming Xu

1 The College of Communications Engineering,Army Engineering University of PLA,Nanjing 210007,China

2 The College of Communications Engineering,Rocket Force University of Engineering,Xi’an 710025,China

Abstract: This paper studies a multi-unmanned aerial vehicle (UAV) enabled wireless communication system, where multiple UAVs are employed to communicate with a group of ground terminals (GTs)in the presence of potential jammers.We aim to maximize the throughput overall GTs by jointly optimizing the UAVs’ trajectory, the GTs’ scheduling and power allocation.Unlike most prior studies, we consider the UAVs’ turning and climbing angle constraints, the UAVs’ three-dimensional (3D) trajectory constraints, minimum UAV-to-UAV (U2U) distance constraint,and the GTs’transmit power requirements.However, the formulated problem is a mixed-integer non-convex problem and is intractable to work it out with conventional optimization methods.To tackle this difficulty, we propose an efficient robust iterative algorithm to decompose the original problem be three sub-problems and acquire the suboptimal solution via utilizing the block coordinate descent(BCD)method,successive convex approximation (SCA) technique,and S-procedure.Extensive simulation results show that our proposed robust iterative algorithm offers a substantial gain in the system performance compared with the benchmark algorithms.

Keywords: anti-jamming; angle constraints; robust design;multi-UAV communications;3D trajectory optimization

I.INTRODUCTION

Due to the characteristics of high altitude, high maneuverability and the desirable unmanned aerial vehicle(UAV)-ground line-of-sight(LoS)channels,UAVenabled wireless communications have gained considerable attention in the fields of social sectors,such as meteorological detection,remote photography,traffic supervision, package delivery, and forest fire prevention[1–4].Compared with terrestrial communication nodes, UAVs can achieve flexible and rapid deployment,thereby provide services to wireless communication without restriction of geographic location.For instance, [2] have presented four representative application scenarios, i.e., UAV as flying BSs, mobile relays,motorial energy sources,and aerial caches,showing the potential of UAV-enabled communications.

Extensive research efforts studies concentrated on the setup with single UAV-enabled communication networks[5–9].[10–14]have confirmed the fact that the multi-UAV enabled wireless communication system can provide a significant performance gain.Reference [10] investigated the trajectory design for a multi-UAV enabled system, which has demonstrated the latter’s effectiveness for improving the system performance by comparing the cases of using a single UAV and its counterpart for multi-UAV.[11]and[12]considered the utilization of full dimension UAV-to-Everything(U2X)communications in the cellular Internet of UAVs,in which the UAVs can support various sensing applications with high transmission rate by adjusting their communication modes full dimensionally.However, the performance enhancements come at a cost.The design of multi-UAV systems are more complicated and need to consider more restrictions,e.g., the collision avoidance constraints, the association, and scheduling considerations between UAVs and ground terminals (GTs).In general, to further enhance the system’s performance, it is a great necessity to investigate the dispatch of multiple UAVs for cooperative communication.In multi-UAV enabled communications,the application of GT-to-UAV(G2U) communication is particularly universal.For example, a mission of survey and data acquisition in sensitive areas(e.g.,real-time crater or battlefield sensor data acquisition),where UAV equipped with sensing devices performs data collection from different GTs to track and capture changing situations in the environment.As a critical factor in determining communication performance,the communication link,i.e.,the channel state,between the GTs and UAVs is most probably depends on UAVs’spatial positions.Therefore,the UAVs’trajectory planning and design is crucial and desirable.

Existing literature on the optimization of UAV networks mainly focuses on the UAV deployment/placement optimization in static-UAV enabled wireless networks[15–17], resource allocation and trajectory optimization in mobile-UAV enabled wireless networks.Furthermore, it has been investigated that the system performance can be vastly improved via the joint optimization of UAV trajectory and relevant wireless resources[10,18–21].For instance,the authors in[10]maximized the minimum throughput in the downlink communication, by jointly optimizing UAV’s trajectory, power control, and ground users scheduling and association.In literature [18] and [19], the system energy efficiency was maximized by jointly optimizing the resource allocation strategy and the trajectory of the information UAV.Reference [20] investigates the multicarrier solar-powered UAV communication systems, which realized the maximization of the system sum throughput by jointly designing the 3D UAV trajectory and the wireless resource allocation.The authors in [21] maximized the system’s throughput via jointly optimizing UAV’s trajectory and transmit power.

However, the attacks from ground transmitters and link interference between UAVs are usually ignored,which is making the trajectory optimization framework effective only in a very narrow scene range.On account of UAVs usually appear at high altitudes and accompanied by the broadcast and the inherent open characteristics of wireless transmission,the UAV-enabled communication systems easily suffer damage from various security threats (e.g., jamming,eavesdropping,and spoofing attacks),which has been theoretically studied[22]and verified by field experiments[23].Among the various security threats, jamming is an active means of attack.A jammer sends a message simultaneously as a legitimator is sending or receiving data, thereby disrupting the transmission of useful data and rendering it impossible for a legitimator to communicate.To be specific, the malicious nodes on the ground or in the air jammer result in the deterioration of communication quality by the same frequency interference worsening the signal-tointerference plus noise ratio(SINR)of the legal communication link.

Recently,some emerging researches have been done to withstand jamming attacks in UAV-enabled communications.The authors in [24] with the aid of cognitive radio and machine learning, proposed a dynamic spectrum anti-jamming(DSAJ)technique withstand increasingly advanced and efficient jamming devices.Reference [25] studied the Bayesian Stackelberg game, which is proposed to formulate the competitive relations between UAVs (users) and the jammer.In order to better characterize the practical scenario, the positional uncertainty of the jammer was considered [26], which is usually resulting in the opposing jammer’s characteristics of camouflage and concealment.However,location uncertainty may lead to channel uncertainty,which will make UAVs trajectory planning more challenging.In this context,robust optimization[27,28]and stochastic optimization theories[29]can be utilized.Among them,the theory of robust optimization involves uncertain parameters in a finite size set, which characterize the error range between the estimated result and the actual value,and it guarantees the feasibility of the solution to all parameters in the finite size set.In addition, the worst-case method is commonly adopted in robust optimization to transform difficult problems into an easy-to-handle form [28].For instance, reference [30] ensured the communication quality of the system via the robust trajectory optimization, and [26] illustrated the superiority and indispensability of robust optimization by the combination of theory and case analysis.

All the above mentioned multi-UAV enabled communications ignored the UAV’s angle constraints.In fact,the UAV’s angle constraints are significant factors for UAV’s behavior, especially concerning the fixedwing UAVs [31, 32].The angle between the UAV’s previous direction and the current direction is called turning angle in the horizontal dimension.The climbing angle has the same role as turning angle in the vertical dimension.For fixed-wing UAVs, their turning angle and climbing angle are limited by the maximum/minimum acceleration.In addition,their trajectory is constrained by nonlinear equations, which results in a fewer degree of freedom of UAV trajectory change.In particular, the scenario that only allows a limited angle change (e.g., a UAV in tight formation,cannot make severe turns and a sharp climb without causing a higher risk of collision),UAVs cannot arbitrarily adjust their flight direction,simultaneously system performance will also be limited.A recent study[33]has studied UAV-to-UAV(U2U)communications with turning angle constraints.The information transmission time was minimized by appropriate optimization of UAVs trajectory and communication resource.Different from [33], in this paper, we investigate the throughput maximization problem for multi-UAV enabled G2U communications in the presence of potential jammers and concurrently consider the turning and climbing angle constraints.The main contributions of this paper are summarized as follows:

• We propose a general multi-UAV enabled optimization framework with potential jammers.By devoting to the uplink information transmission,our target is to maximize the throughput overall GTs via considering the UAVs’ turning and climbing angle constraints, 3D trajectory constraints, GTs’ scheduling constraints, transmit power constraints, the minimum U2U distance,and the location uncertainties of jammers.This work fully considers the UAVs’ maneuverability constraints,the complex conditions in the realistic environment, and takes full advantage of UAVs’high mobility characteristic, which significantly expands the applicable range of UAVs and gives full play to its potential.

• Due to the coupling of the variables, the nonlinearity of the turning and climbing angle constraints, the binary variables for GTs’ scheduling,the uncertainty of the jammer’s location,and the non-convexity of the objective function, it is challenging to solve the design optimization problem.To overcome the difficulties, we develop a robust iterative algorithm.By leveraging the block coordinate descent(BCD)method,successive convex approximation (SCA) technique,Sprocedure,Young inequality,and introducing the slack variables, we receive the suboptimal solution of the original problem.In addition,We testify the convergence and the complexity of the proposed algorithm.

• Further, extensive simulations are provided to show the influence of the angle constraints and uncertain position of jammers on the UAVs’ behavior and system performance.The simulation results demonstrate that the robust iterative algorithm offers a substantial gain in the system performance compared with the benchmark algorithms, which gives a specific practical significance for multi-UAV networks’ trajectory and communication design.

The remainder of this paper is organized as follows.In Section II and Section III,we introduce the system model for the multi-UAV enabled uplink communications and formulate the optimization problem.In Section IV,the robust iterative algorithm is proposed,and the convergence and complexity are illustrated simultaneously.Section V provides extensive simulation results to verify the effectiveness of the proposed algorithms.Finally, Section VI summarizes the conclusions of this paper.

Notations: Boldface lower-case letters are used to denote vectors.RM×1denotes theM-dimensional real-valued vector.Given a vectorξ,∥ξ∥andξ†denote its Euclidean norm and transpose,respectively.

II.SYSTEM MODEL

We consider a UAV-assisted uplink system illustrated in Figure 1,where UAVs gather information from GTs in the presence of jammers.The locations of GTs are knowable for UAVs, while only the estimated locations of jammers can be obtained, which is more practical for most application scenarios.LetK,JandUdenote the sets of GTs, jammers, and UAVs,respectively, where|K|=k,|J|=jand|U|=u.We consider the 3D Cartesian coordinate system,and denote the positions of GTs, jammers and UAVs as qk ∈R3×1, qj ∈R3×1and qu ∈R3×1.Concretely, the positions given as qk={xk,yk,zk},qj={xj,yj,zj}, and qu={xu,yu,zu}, respectively.We assume a hemisphere as the jammers’ uncertain region [26].Suppose that only the estimated position of jammers,i.e.,the center of the hemisphere,can be obtained as qjc={xjc,yjc,zjc}.Hence, we have

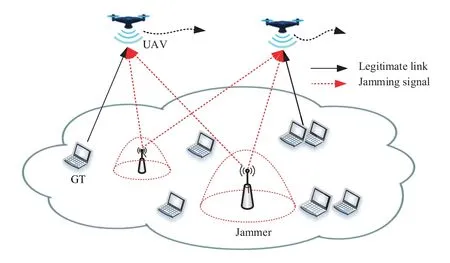
Figure 1. System model.

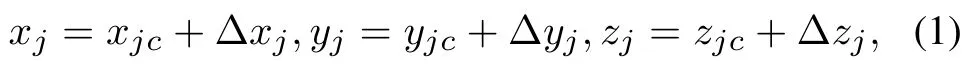
where (∆xj,∆yj,∆zj)∈∆qjis the errors between the estimated position and the exact position,which is limited by

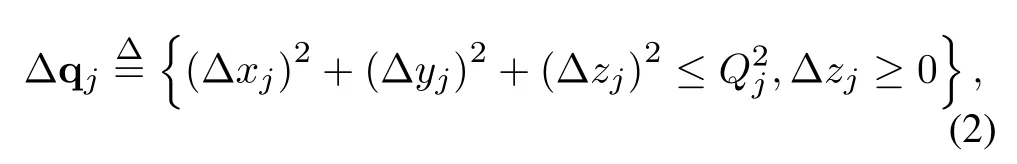
whereQjis the radius of the hemisphere.

Each UAVu ∈|U|is scheduled to complete the given collection task within a limited time periodT.We denoteandas the UAV’s starting-point and ending-point,respectively.To tackle the challenge of the continuous nature of the variableT, we discretizeTintoNequal quasi-static time slots ∆t,i.e.,T=N∆t.We can express the UAV’s trajectory as

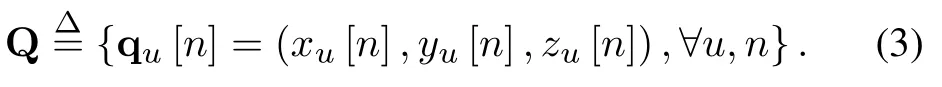
In this paper, a proactive trajectory optimizing scheme is considered, and we assume that LoS links dominate the channels from the GTs and jammers to the UAV.On account of the practical field measurements for air-to-ground (A2G) channels have shown that the A2G communication channels are mainly dominated by the LoS links when the UAV is beyond a moderate height[1,34,35].The LoS probability of A2G links in a rural environment exceeds 95 percent for a horizontal ground distance of 2 kilometers when UAV’s height is beyond 80 meters[36].In this paper,the UAV is arranged at an altitude between 100 meters and 200 meters around a rural-like area for its flying mission.It can be assumed that the channel quality depends only on the distance from the UAV to GTs,which is highly predictable.Thus, we consider LoS propagation between the GTs and the UAV.The channel power gains at the time slotncan be modeled as the free-space path loss model,i.e,

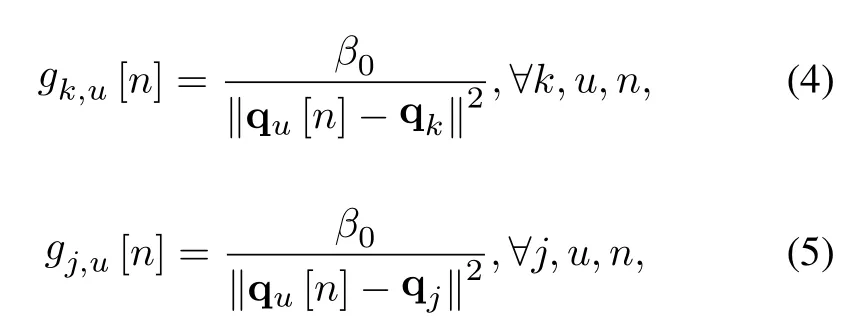
whereβ0represents the channel power gain at 1 meter.We assume that the Doppler effect can be eliminated by adopting relative technical measures[37].

The UAV’s 3D trajectory constraints are given as

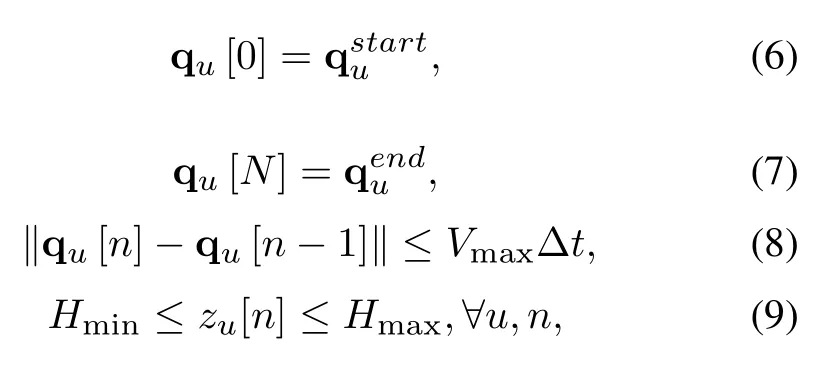
whereVmaxis the UAV’s maximum flying speed,Hmindenotes the minimum flying altitude, andHmaxdenotes the maximum flying altitude.Assume that the UAVs operate at orthogonal frequency channels for their communications with the GTs.At each time slot,one GT can be scheduled transmitting information to at most one UAV and one UAV can gather information from at most one GT.Define a binary variable B{bk,u[n],∀k,u,n},wherebk,u[n] = 1 indicates that the GTkcommunicates with the UAVuat time slotn,andbk,u[n] = 0,otherwise.Then,we have the scheduling constraints as

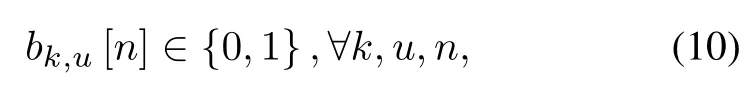
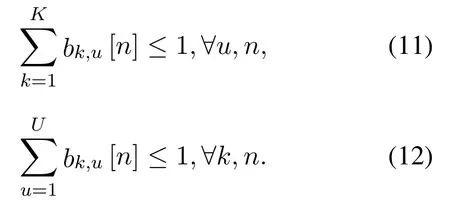
Taking into account the energy constraint of GT,we denote P{Pk[n],∀k,n}as the GT’s transmit power in time slotn.Then,the GT subject to the transmit power constraints

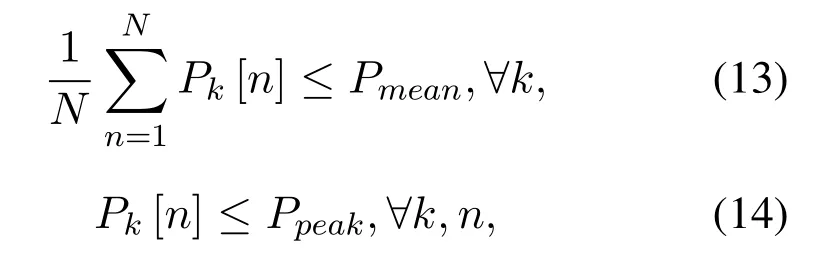
wherePmeanis the average GT transmit power andPpeakis the peak GT transmit power.Constraint(13)means that the GT has a limited total energyNPmean.

Letαandϕbe the UAV’s turning and climbing angles.Set

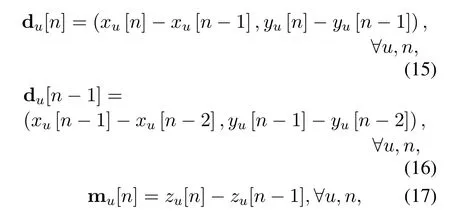
then by the definitions of turning angle and climbing angle,we have

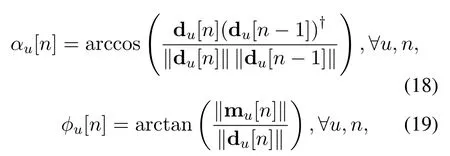
where 0≤α ≤180◦and 0≤ϕ ≤90◦.Specifically,α=180◦andϕ=90◦is the case of no turning and climbing angle constraints, which correspond to rotary-wing UAVs.Thus, we can express the UAV’s turning and climbing angle constraints as

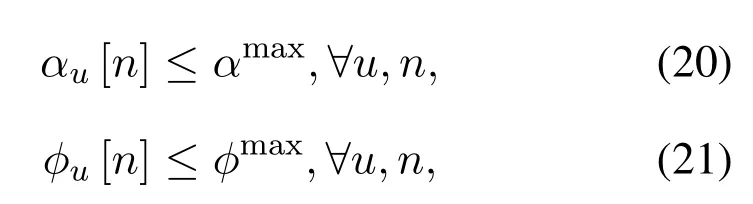
or the following equivalent form

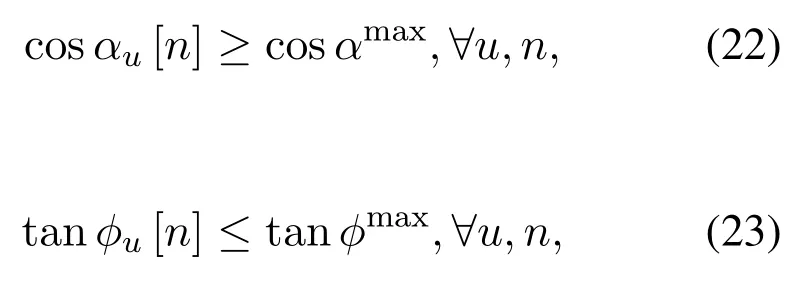
whereαmaxandϕmaxare the UAV’s maximum turning angle and climbing angle.

Ensuring UAVs’safe operation is the basic premise of multi-UAV enabled networks, e.g., sufficient safe distance should be kept between UAVs.To this end,a minimum distance is set as

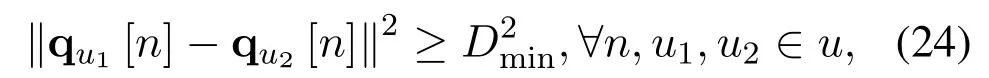
whereDminis the minimum distance allowed between UAVs.

The instantaneous uplink throughput in time slotncan be expressed as

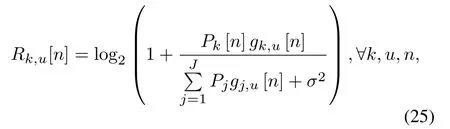
whereσ2denotes the power of additive white Gaussian noise(AWGN)at the receiver,andPjdenotes the jammer’s transmit power.

III.PROBLEM FORMULATION

In the presence of malicious jammers,the system performance will be seriously degraded.It is indispensable to design the UAVs’ trajectory to keep it away from malicious jamming but not too far from the GTs.Meanwhile,by optimizing the transmit power,the GTs can allocate the transmit power as much as possible to the time slot at the best position of the UAV for information transmission, thereby improving the system’s performance.Thus,we jointly design the UAVs’trajectories,GTs’scheduling,and power allocation to maximize the system’s throughput.Based on(25),the achievable throughput of the system in time periodTis written as

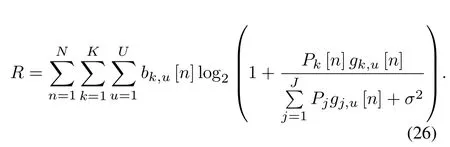
Then, the problem of maximizing the throughput can be denoted as(27):

Due to the coupled optimization variables and the estimation error of the location of jammers in (27a),the binary variables for GTs’ scheduling in (27f),(27g) and (27h), the angle constraints which consist of nonlinear functions in(27k)and(27l),and the nonconvexity of the function in (27a), (27m), it is intractable to work out the problem(27).Thus, finding the optimum solution effectively for (27) is challenging.

IV.ROBUST ITERATIVE ALGORITHM

We can notice that the original optimization problem can be divided into three blocks by utilizing the BCD method.We solve(27)by iteratively solving the three sub-problems: optimizing Q with given P and B,optimizing B with given Q and P, and optimizing P with given Q and B.Until the objective function’s value increases below an accurate tolerance.In the following work, we will put forward a robust iterative algorithm and elaborate on it.In addition,we will summarize the overall algorithm and illustrate its convergence and computational complexity.

Since the non-convexity of the objective function,we introduce a slack variableη.Without loss of optimality,the problem(27)can be reconstructed as(28)

(27b)−(27m).

4.1 Sub-problem 1: Optimizing Trajectory with Given Scheduling and Transmit Power.

For given the GTs’ scheduling B and transmit power P,the problem(28)can be denote as

(27b)−(27e),(27k)−(27m).

The angle constraints in(27k)and(27l)are nonlinear.They can be reformulated as

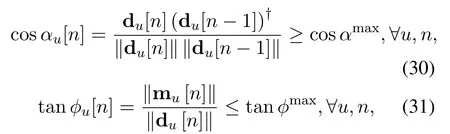
or the following tractable form

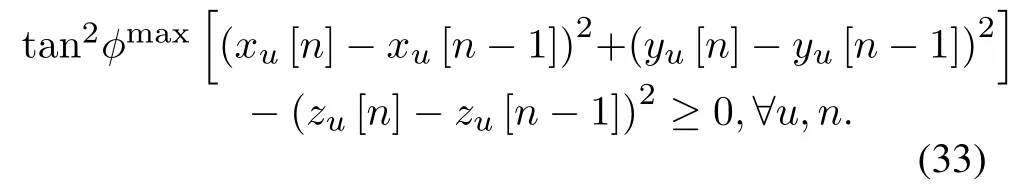
In (32), the terms du[n](du[n −1])†and∥du[n]∥∥du[n −1]∥can be addressed by the following proposition and Young inequality,respectively.

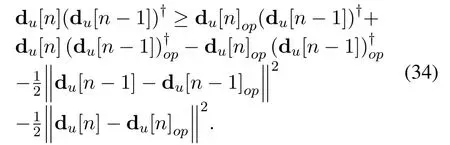
Proof.: Please refer to Appendix C of[38].

Young inequality[39]: DenoteG,Θ,τandςas the conjugate function,l×lpositive definite matrix and arbitrary variables, respectively.For anyτandς, the following equation hold

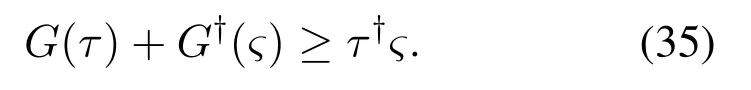
DenoteG(τ)=(1/2)τ†Θτ,there is

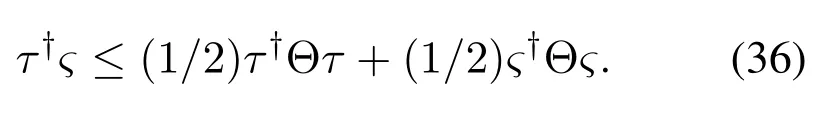
For∥du[n]∥∥du[n −1]∥cosαmax,by applying the Young inequality(36),we have

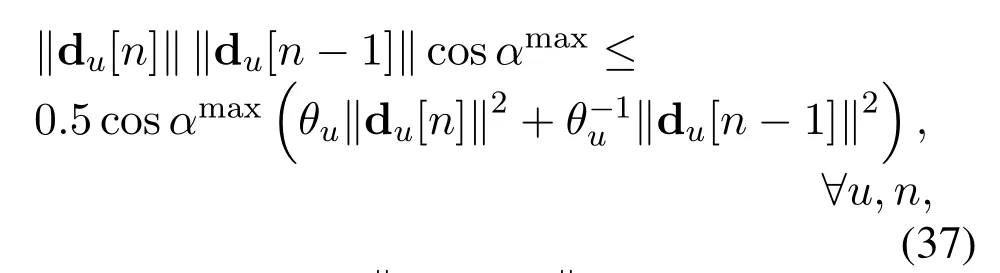
whereθucan be∀u,n.By leveraging(34)and(37),the constraint(27k)can be rewritten as

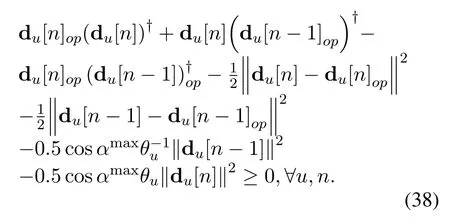
Regarding (33), the termξ2is a convex function w.r.t.ξ, by applying the first-order Taylor expansion to the terms (xu[n]−xu[n −1])2,(yu[n]−yu[n −1])2and (zu[n]−zu[n −1])2, the lower bound of(33)can be obtained as

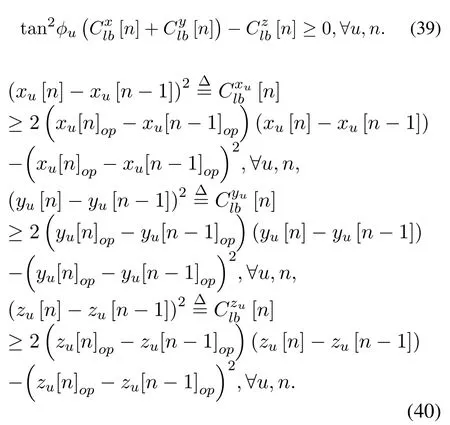
The minimum U2U distance constraint in (27m)also is non-convex,and can be rewritten as

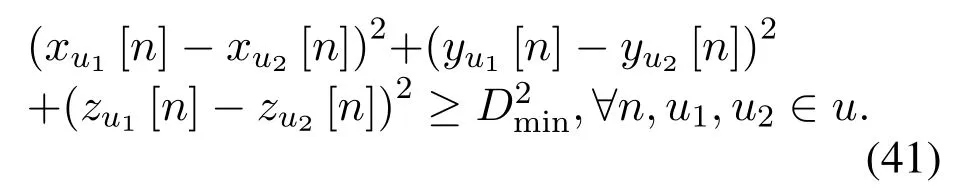
By applying the first-order Taylor expansion to the terms (xu1[n]−xu2[n])2, (yu1[n]−yu2[n])2, and(zu1[n]−zu2[n])2, the lower bound can be obtained as

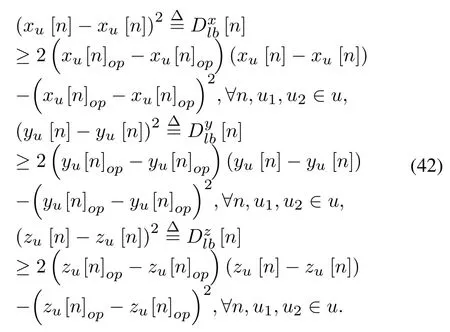
Then,constraint in(27m)is lower bounded by

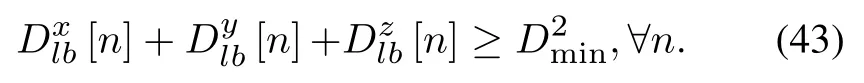
Thus,(29)can be written as:

(27b)−(27e),(38),(39),(43).

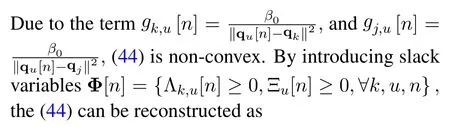
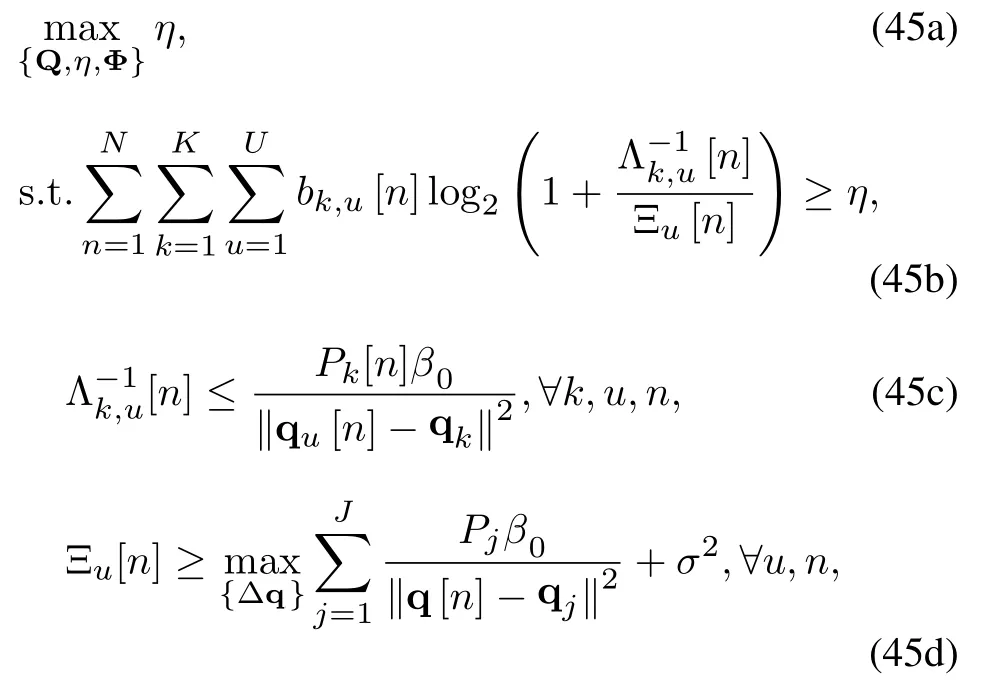
(27b)−(27e),(38),(39),(43).

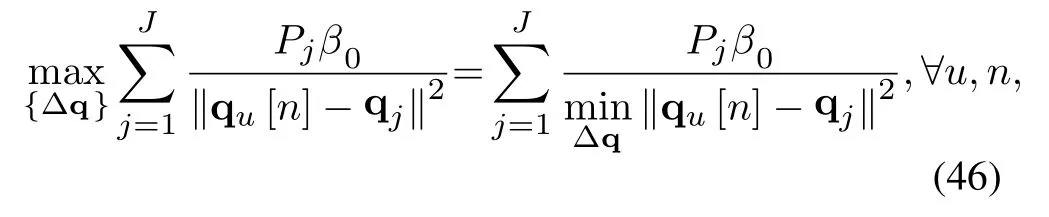
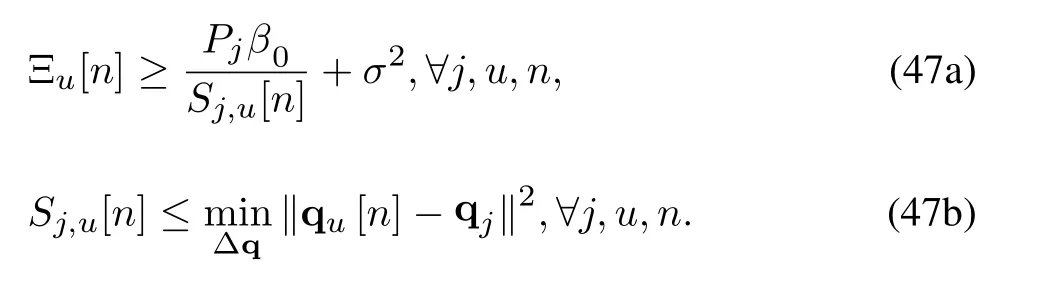
Further,(47b)is equivalent to

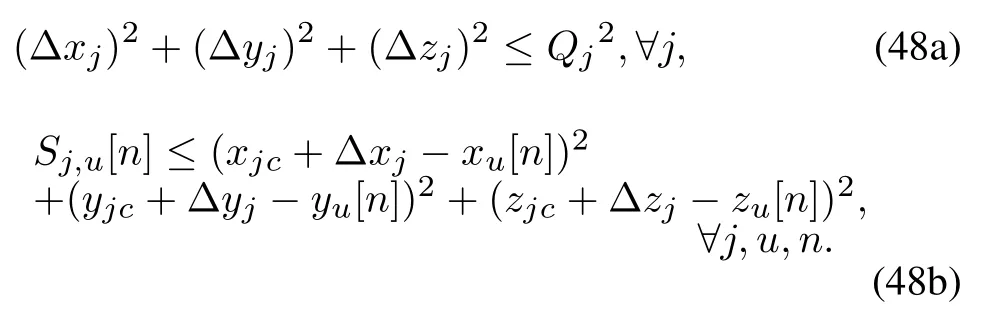
S-Procedure [39]: LetFi, ri,andhias thew×wsymmetric matrix,wdimensional column vector,and real number, respectively.We suppose there existswith

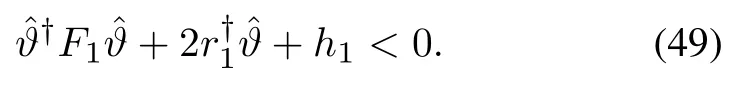
Then there existsϑsatisfying

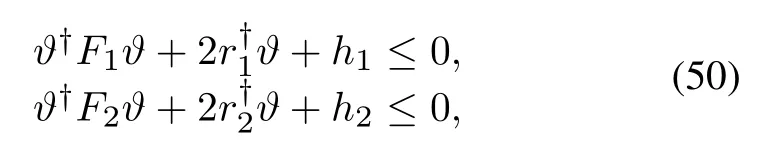
if and only if there is aλ≻0 such that

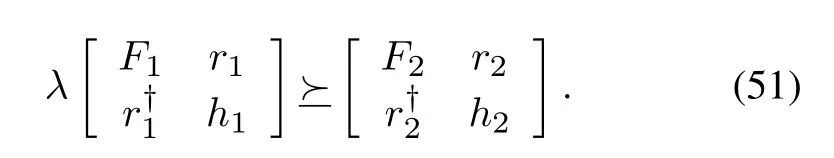
Thus, by leveragingS-Procedure, we can hold the following implication

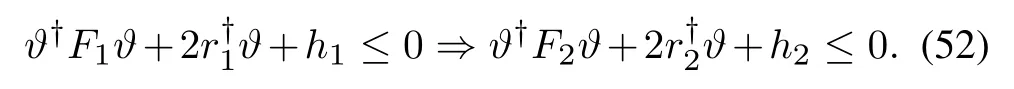
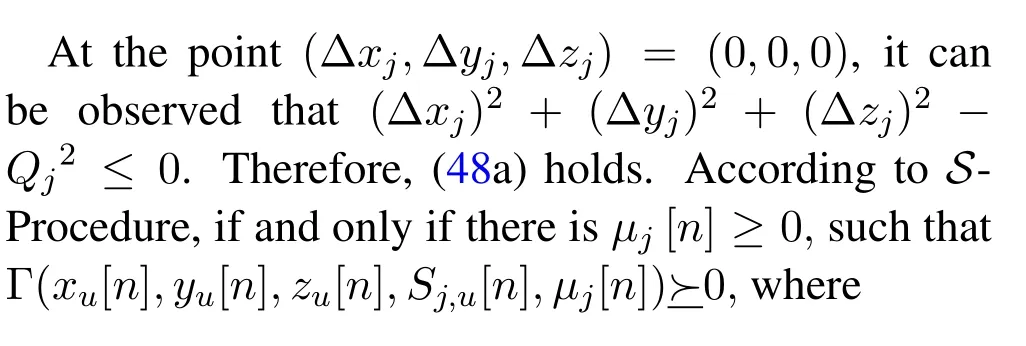
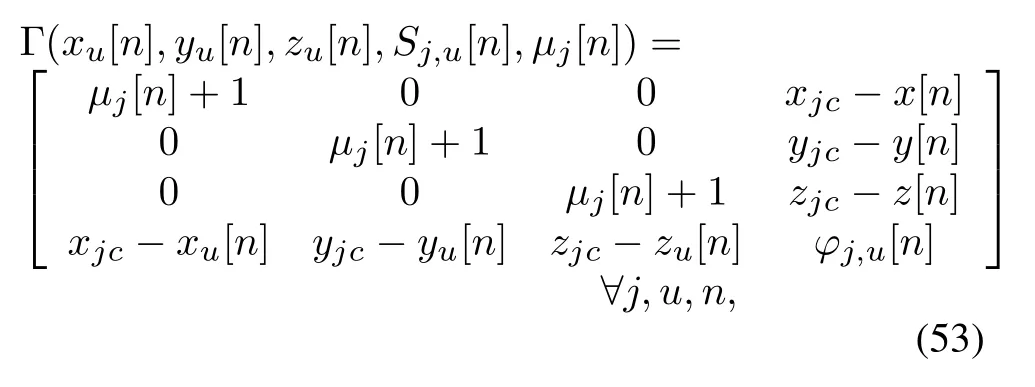
with

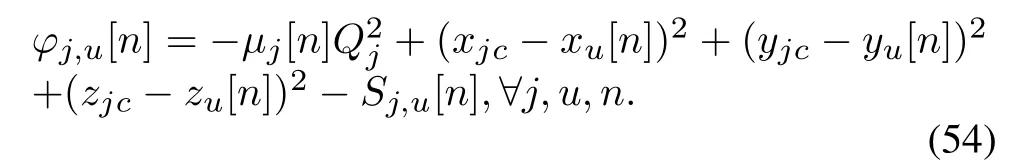
(48a)implies(48b).

By introducingS-Procedure, we transformed the uncertain position constraint(45d)into a definite constraint.To proceed, we can work out the original problem by dealing with a semidefinite programming problem.(53) is still tricky since the non-convexity.The termξ2is a convex function w.r.t.ξ, at a given point (xu[n]op,yu[n]op,zu[n]op),the lower bound of the terms[n],[n],and[n]can be obtained by utilizing the first-order Taylor expansion,i.e,

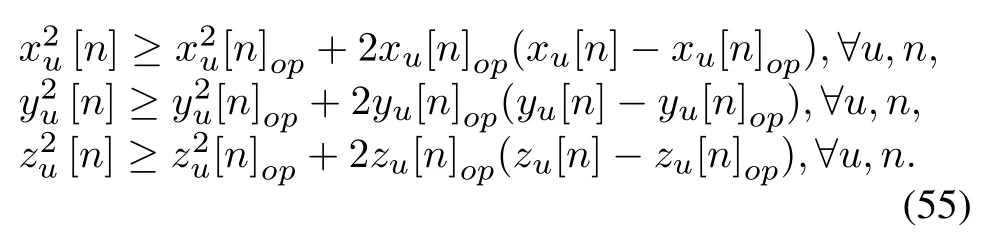
Thus,(54)can be reformulated as

Lemma 1.The term

implies that

where

Proof.Please refer to Appendix B in[37].

For constraints(45b)and(45c), since the log2(1+is a convex function w.r.t.xandy,there have

where

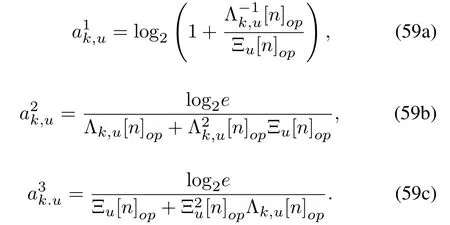
To proceed,(45c)can be converted into

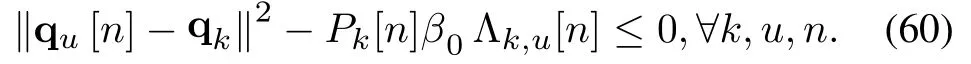
Hence,(45)can be reformulated as:

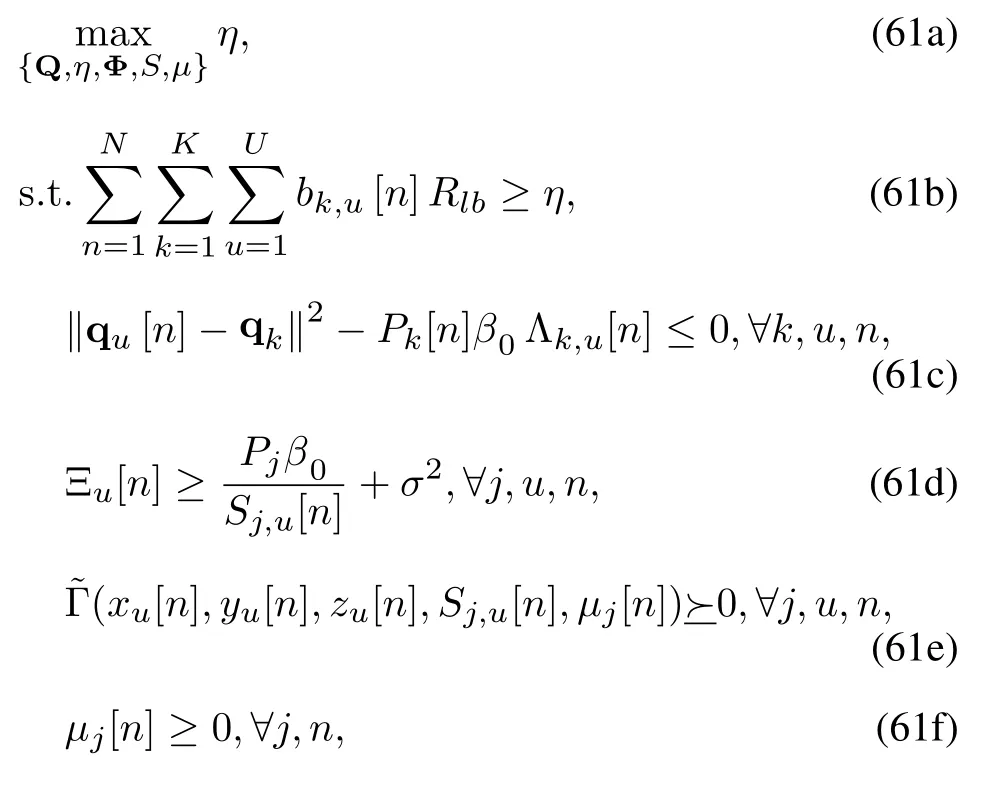
(27b)−(27e),(38),(39),(43).

Problem (61) is a semidefinite optimization problem.We can solve it effectively by optimization solvers,such as CVX[40].

4.2 Sub-problem 2: Optimizing Scheduling with Given Transmit Power and Trajectory.

For given Q and P, to deal with the uncertainty of the jammer’s location, we consider scheduling optimization under the worst-case, where the jammer is located closest to the UAV in the range of uncertainty.Next, in order to tackle the binary variables B, we relax it into continuous variablesTherefore,problem(28)can be rewritten as

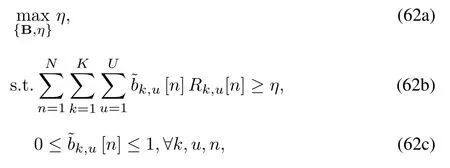
(27g),(27h).

This relaxation implies that the optimal solution to(62) provides an upper bound for that of (28).Then,we introduce a penalty term to the objective function(62a) [27], which guarantees[n] approaches to 0 or 1.Hence,problem(62)can be transformed as

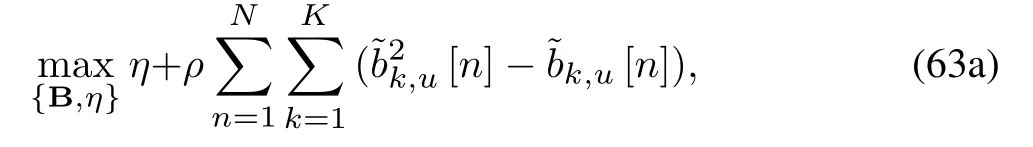
s.t.(27g),(27h),(62b),(62c),

Thus,(63)can be reformulated as

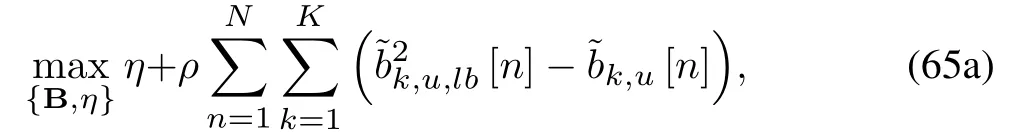
s.t.(27g),(27h),(62b),(62c).

Problem(65)is a standard linear programming(LP)problem, which can be solved via existing optimization tools such as CVX[40].

4.3 Sub-problem 3: Optimizing Transmit Power with Given Trajectory and Scheduling.

For given Q and B, like Sub-problem 2, we deal with the uncertain region by considering the worstcase, i.e., in the uncertain region, the jammer is always located closest to the UAV.Problem(28)can be expressed as

(27i),(27j),

It is a normative convex optimization problem.We can solve it effectively by CVX[40].

4.4 Overall Algorithm

In summary,we divide the original problem(28)into three blocks by utilizing the BCD method.In addition, with the aid of slack variables, SCA technique andS-procedure,Sub-problem 1,Sub-problem 2 and Sub-problem 3 are solved as shown in(61),(65),and(66), respectively.We solve them until the objective function’s value increase below an accurate tolerance.Algorithm 1 gives the proposed algorithm.

Algorithm 1. Robust iterative algorithm for Problem(27).1: Initialization: set the iteration number i = 0,initialize a feasible solution(Q(i),B(i),P(i))and the accuracy tolerance ε.2: Repeat:3: Solve the semidefinite optimization problem in(61) and obtain the optimal solution Q(i+1) with given P(i)and B(i).4: Solve the standard linear programming problem in(65)and obtain the optimal solution B(i+1)with given Q(i+1)and P(i).5: Solve the standard convex optimization problem in(66)and obtain the optimal solution P(i+1)with given Q(i+1)and B(i+1).6: Update i=i+1.7: Until the objective function’s value increases below the accurate tolerance ε.

4.4.1 Convergence Analysis of Algorithm 1

Because of the constraint (27i) in problem (27), i.e.,the GTs’transmit power can not increase unlimitedly,thereby the target value has an upper bound.To proceed,we will demonstrate that the lower bound of the target value will not decrease in each iteration.We assume that the objective values of (61), (65) and (66)areR(Q(i+1),B(i),P(i)),R(Q(i+1),B(i+1),P(i))andR(Q(i+1),B(i+1),P(i+1)), respectively.Firstly,for given B(i)and P(i), and the initial pointR(Q(i),B(i),P(i)) in (28), based on (40), (42), (55)and(58),we obtain

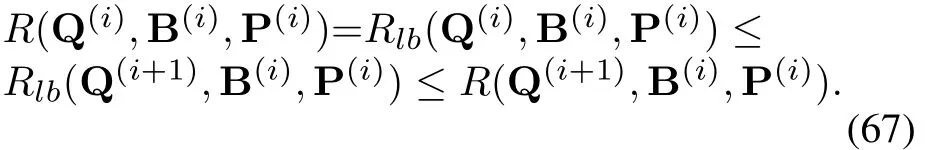
Secondly, for given Q(i+1)and P(i), for the same reasons,we have

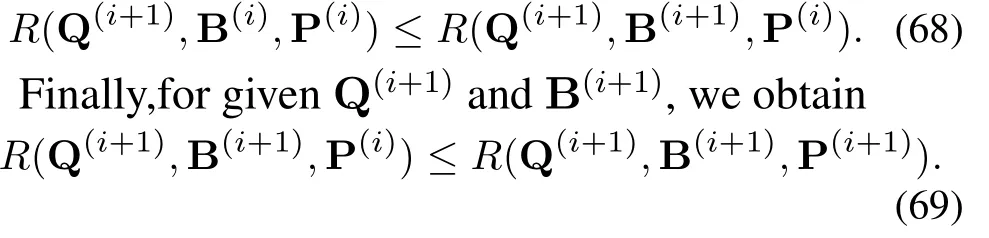
According to(67)-(69),we can receive

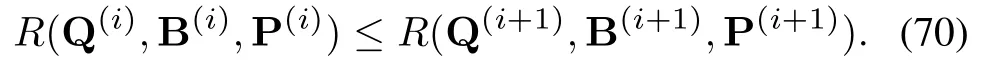
(70)indicates that the target value of(28)has not decreased after each iteration.The convergence of Algorithm 1 is guaranteed.

4.4.2 Complexity Analysis of Algorithm 1

V.NUMERICAL RESULTS

In this section,simulation results are presented to confirm the effectiveness of the proposed robust iterative algorithm.To show the UAVs’ trajectory clearly and concisely, we assumeU= 2,K= 4, andJ= 2 in this paper.Notice that the proposed algorithm works well with any numbers of UAVs and GTs,which can be extended into the case where the number of UAVs and GTs are different.The starting-points and the ending-points of UAV 1 and UAV 2 are set as (50,100,200), (450,−100,200), (50,−100,200),and (450,100,200), respectively.Consider an initial path to start the proposed algorithm where the UAVs fly from the starting-points to the ending-points in a straight line.Furthermore, UAV 1 is associated with GT 3 and GT 4, and UAV 2 is associated with GT 1 and GT 2, respectively.Simultaneously, each GT is transmitting information with the average power, i.e.,Pmean.Four benchmark algorithms are introduced as comparisons.The initial path is denoted as“No opt.”,which is used as a benchmark scheme.The algorithm that only optimizes the trajectory is called“Only Tra.”.In addition, we consider the scenarios “Jammers appear with estimated locations” and “No error exists”.Specifically, when we assumeQ1= 0 andQ2= 0, the scenario of “Jammers appear with estimated locations”degrades to the exceptional scenario,i.e.,“No error exists”,which is one of the benchmark algorithms.When there are no angle constraints, i.e.,α=180◦andϕ=90◦,which is denoted as“No angle”.Note that we denote Algorithm 1 as“Joint”.Other system parameters are given as follows.We assume that the G2U channel is allocated with a unit bandwidth.We setT= 20 s and ∆t= 0.5 s,thereby the number of discrete values isN= 40.The positions of GT 1 to GT 4 are set as (100,−200,0),(200,50,0), (100,200,0), and (400,−200,0), respectively.The estimated position of jammer 1 and jammer 2 are (100,−50,0) withQ1= 30 m, and(400,50,0)withQ2=60 m,respectively.The UAVs’flying altitudes and speed are assumed asHmin=100 m,Hmax= 200 m,andVmax= 60 m/s,respectively.The jammers’ transmit power and the GTs’ transmit power are set asPm= 0.4 W,Pmean= 0.2 W,andPpeak= 0.5 W, respectively.The noise power isσ2=−169 dBm/HZ.The channel power gain at the reference distance 1 meter is set asβ0=−30 dB.The collision avoidance minimum distance and convergence accurate tolerance are set asDmin= 10 m andε= 10−3, respectively.In addition, we assumeαmax=ϕmax= 45◦as the maximum turning angle and climbing angle constraints.

5.1 Trajectory and Communication Design

Figure 2 shows the UAVs’ behaviors under the settings ofQ1= 30,Q2= 60,αmax=ϕmax= 45◦.The following behaviors can be observed: It is first observed that the UAVs fly in a curve.The UAVs reach the vicinity or right above the GTs.That is to say, the UAVs tend to approach the GTs and fly at a lower flying altitude to enhance the information transmit by reducing the distance between each other.Simultaneously, the UAVs also use their best efforts to avoid the jammers to mitigate the effects of jamming signals.The reason is as follows: the channel states are closely related to the distance between the UAVs and the GTs.The channel states are of better quality with a reducing distance and vice versa.Therefore,the UAVs will hover at the minimum flying altitude while directly above the associated GTs, where much more information can be transmitted with the better channel states.In addition,the instantaneous distance between UAV 1 and UAV 2 is shown in Figure 3,which demonstrates the flying security of the proposed algorithm.It can be obviously observe that the distance between the UAV 1 and UAV 2 varied with time and always exceeded the minimum security distance.Therefore,the trajectories of UAVs satisfied the collision avoidance constraint in every time slot.

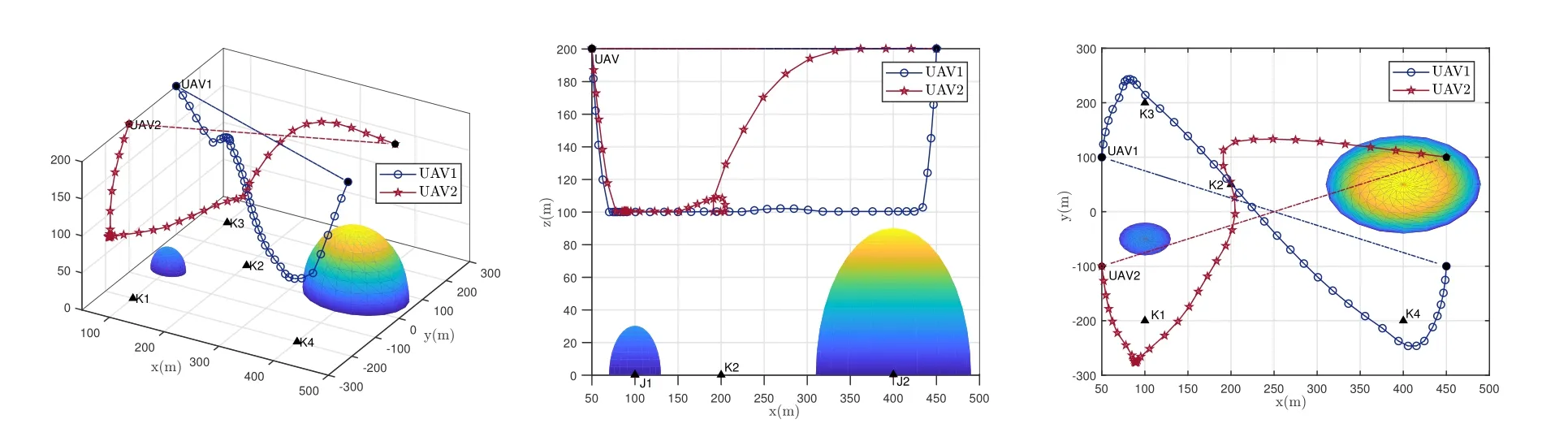
Figure 2. UAVs’behaviors under the cases of Q1 =30,Q2 =60,αmax =ϕmax =45◦in different views.

Figure 3. The distance between the two UAVs under the case of Q1 =30,Q2 =60,αmax =ϕmax =45◦.

Figure 4 shows the impact of turning and climbing angle constraints on UAVs’behaviors.Setting the maximum turning angle and climbing angle parameters asαmax= 180◦,ϕmax= 90◦(“No angle”) andαmax=ϕmax= 45◦,which correspond to fixed-wing and rotary-wing UAVs, respectively.We can observe that the trajectory change ofαmax=ϕmax= 45◦is more smooth compared withαmax= 180◦,ϕmax=90◦.Furthermore, in both horizontal and vertical dimensions,drastic trajectory changes are avoided with the settings of angle constraints, which demonstrates the effectiveness of our proposed algorithm.Consider the maneuverability restriction of UAVs,it is desirable to reduce the collision risk in the cases of tight formation, thereby the design of angle constraints is indispensable.Figure 5 shows the trajectories of UAVs while faced with different jamming uncertain ranges,for instance,Q1= 0, Q2= 0 (“No error exists”),Q1= 30, Q2= 60 andQ1= 30, Q2= 90.It can be seen that with the range of uncertainty increases,the UAVs will fly farther away from the jammer.That can be construed as the following perspectives.On one hand, within the uncertainty range, the presence of jamming signals is assumed, which is the lower bounded of our proposed robust iterative algorithm in practice.Furthermore, the larger the radiuses of the uncertain range, the greater the effects of jamming signals.On the other hand, whenQ1= 0,Q2= 0(“No error exists”),which corresponding to the nonrobust scenario, it is the upper-bounded in all cases.The UAVs’trajectories in Figure 5 are consistent with expectations,which verifying the effectiveness of our proposed robust optimization.

Figure 4. UAVs’ behaviors under the cases of αmax =180◦,ϕmax = 90◦and αmax = ϕmax = 45◦with Q1 =30,Q2 =60 in different views.

The optimizing design of the transmission power and the scheduling of GTs under the setting ofQ1=30,Q2= 60,αmax=ϕmax= 45◦are investigated,which are plotted in Figure 6 and Figure 7, respectively.(Figure 7 converted the GTs’scheduling to different colors according to their values,and dyed with these colors at corresponding positions on the coordinate axis.For instance, when the schedule value is 1, the color block appears blue, and when the schedule value is 0,it appears red).Combined with the trajectories in Figure 2, it is first observed that the GTs’transmission power will be at or near the maximum for information transmission once they are associated with the UAVs.Specifically, GT 1 is associated with UAV 2 in the first half of the whole time slots and then associated with UAV 1 in the rest time slots for a period of time.When GT 1 is associated with UAV 2,the UAV 2 is hovering over GT 1,and GT 1 transmits information with maximum transmit power, which is as expected.However, when GT1 is associated with UAV1,no information is transmitting during this time.This is mainly due to the fact that the deterioration of the legitimate communication link as a consequence of the comparative distance between GT 1 and jammer 1,GT 1 and UAV 1.For the same reason, when UAV 1 and UAV 2 fly to the ending-points in the last 5 to 10 time slots, the transmission power of GT 2 and GT 4 are reduced to the minimum.

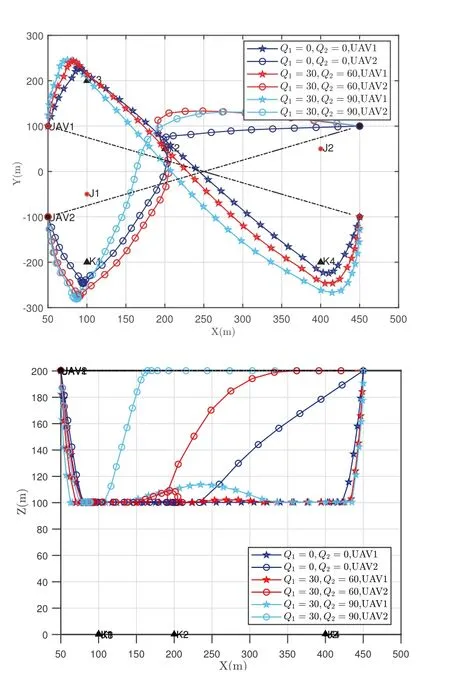
Figure 5. UAVs’ behaviors under the cases of Q1 = 0,Q2 = 0,Q1 = 30,Q2 = 60 and Q1 = 30,Q2 = 90 with αmax =ϕmax =45◦in different views.

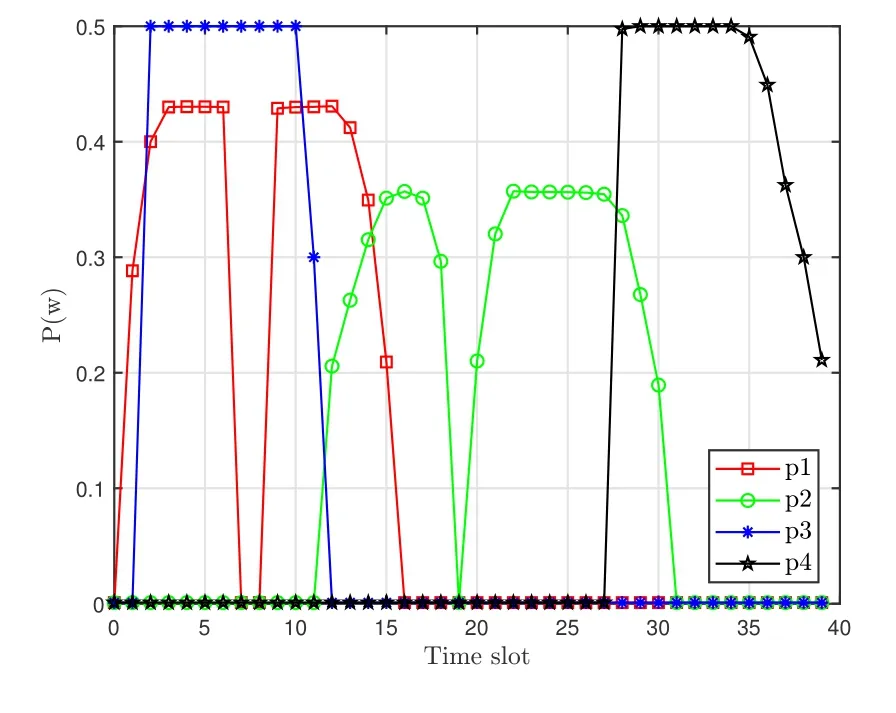
Figure 6. GNs’transmit power under the setting of Q1 =30,Q2 =60,αmax =ϕmax =45◦.

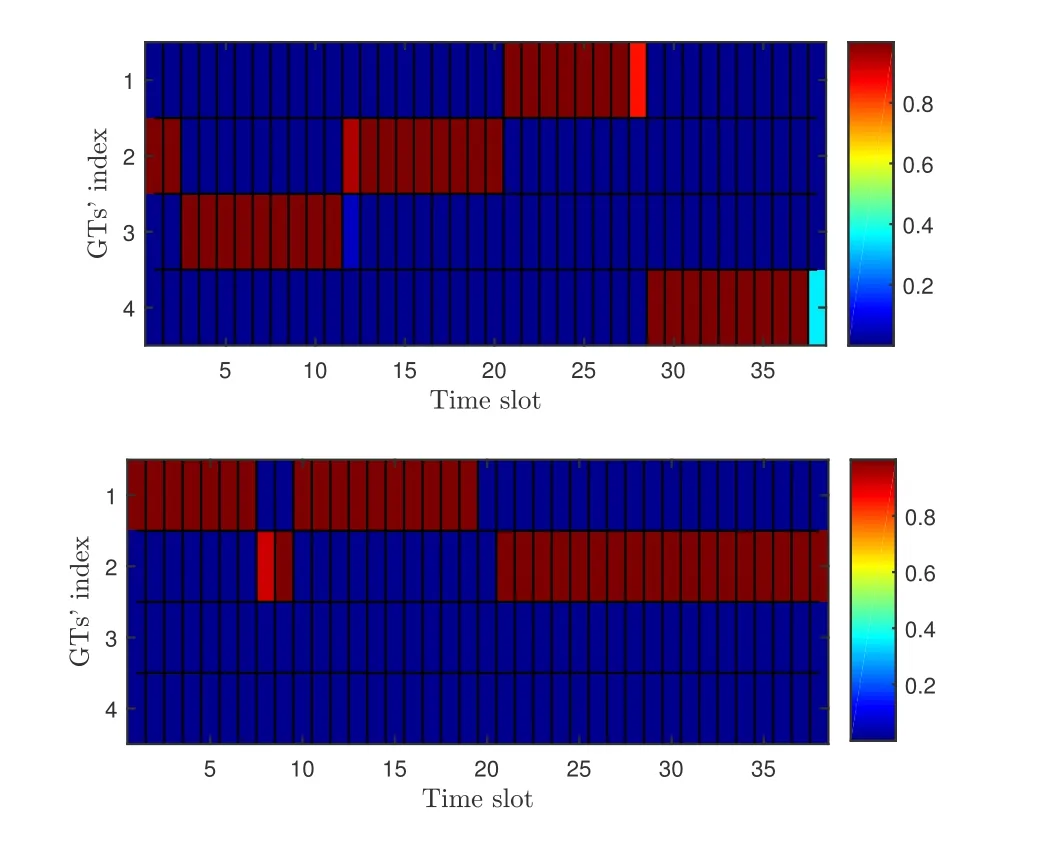
Figure 7. GTs’ scheduling with UAVs under the setting of Q1 =30,Q2 =60,αmax =ϕmax =45◦.

5.2 Performance Comparison and Verification

Figure 8 illustrates the convergence behavior of the proposed robust iterative algorithm under different parameter settings.It illustrates that with the number of iterations increasing, our proposed algorithm converges to the optimal values.Within ten iterations,Algorithm 1 achieves convergence.In addition,the optimal value is non-decreasing over the iteration number.Therefore, the simulation results satisfy our expectations and verify the convergence of the proposed algorithm.

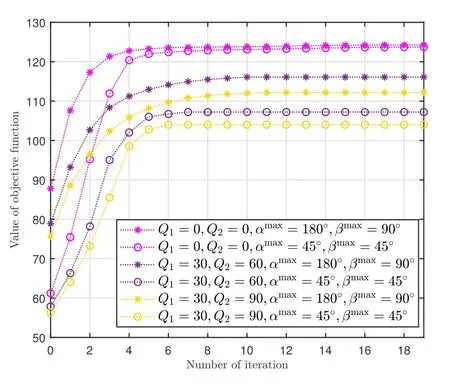
Figure 8. Convergence behaviors of Algorithm 1.

Figure 9 shows the throughput overall GNs’derived by different algorithms (“No error exists”, “Joint”,“No opt.”, “Only Tra.”), and investigates the impact of the uncertain position of jammers under different parameter settings.It is first observed that the throughput is improved as the task completion time increases in all cases.Further, it can be found that the “Joint”algorithm significantly outperforms the benchmark algorithms of “No opt.” and “Only Tra.” in all settings, which illustrates the superiority and effectiveness of Algorithm 1.Moreover, Figure 9 presents the throughput under the cases ofQ1= 0,Q2= 0,Q1= 30,Q2= 60, andQ1= 30,Q2= 90, which correspond to“No error exists”and“Jammers appear with estimated locations”, respectively.Contrasted with the “Jammers appear with estimated locations”,the scenario of“No error exists”vastly enhances the system’s throughput, which indicates the fact that the imperfect location of the jammers will degrade the system performance.All the above mentioned conclusions imply the indispensability of the joint optimization of UAVs’trajectories,GTs’scheduling and power allocation.

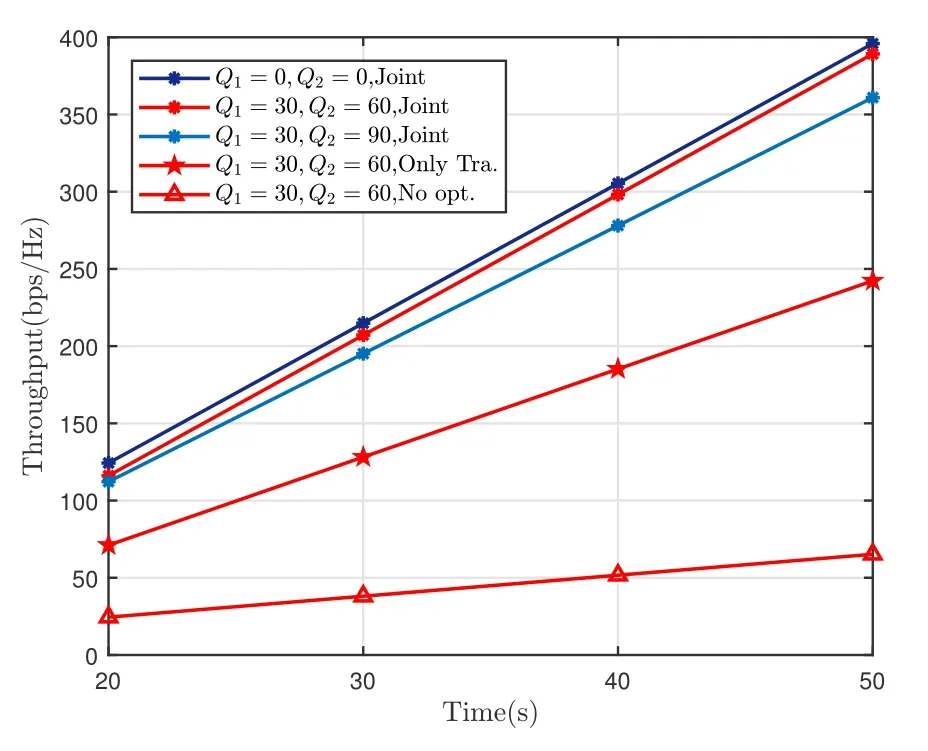
Figure 9. System performance versus time with αmax =180◦,ϕmax =90◦.

Finally, we compare the relationship between system performance and the jammers’ transmit powerPm.From Figure 10, we can observe that the performance under all parameter settings have a decrease when the jammers’ transmit power increase, which demonstrates the devastating effect of jamming on information transmission of wireless communications,and simultaneously confirms our conclusions in Figure 2 and Figure 9.

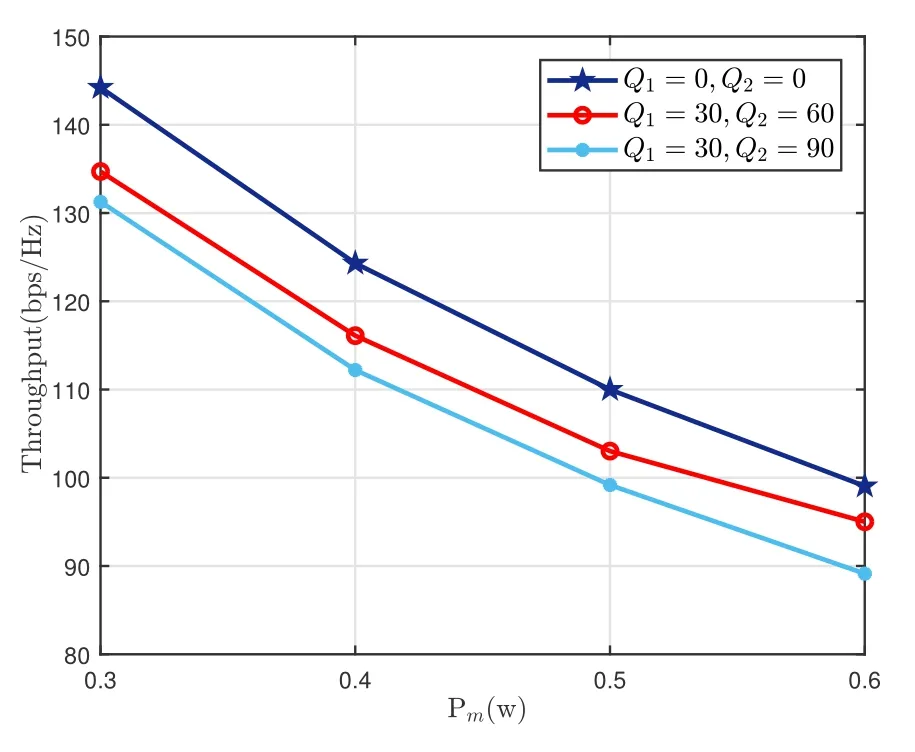
Figure 10. Throughput under different settings versus Pm with αmax =180◦,ϕmax =90◦.

VI.CONCLUSION

In this paper, we investigated the multi-UAV enabled wireless communications with the presence of potential jammers, where the GTs were transmitting information to the UAVs with turning and climbing angle constraints.With the utilization of BCD method,SCA technique, andS-Procedure, a robust iterative algorithm via jointly optimizing UAVs’trajectories, GTs’scheduling and power allocation has been developed.Simulation results demonstrated that contrasted with the benchmark algorithms, our proposed robust iterative algorithm can significantly improve the system performance.Instructively,it was also confirmed that the angle restrictions are considerable for the multi-UAV enabled wireless communication networks.In the future, we will extend the results of this paper to the energy-efficient UAVs’ trajectories design and communication resource allocation by considering the UAVs’stringent size,weight and power(SWAP)constraints[1].