Successive Interference Cancellation and Alignment in K-User MIMO Interference Channels with Partial Unidirectional Strong Interference

Long Suo,Hongyan Li,Shun Zhang,Jiandong Li

1 State Key Laboratory of Integrated Service Networks,Xidian University,Xi’an 710071,China

2 Guangzhou Institute of Technology,Xidian University,Guangzhou 510000,China

Abstract: Recently cellular networks have been densely and heterogeneously deployed indoors and outdoors to expand the network capacity,and thus the in-building propagation loss and the transmit power diversity of access points will exacerbate link heterogeneity and result in partial unidirectional strong interference.To make full use of the strong interference feature, we propose the successive interference cancellation and alignment(SICA)scheme in the K-user interference channel with partial unidirectional strong interference.SICA is designed to transmit two kinds of data streams simultaneously,the alignment streams and superposition streams.The alignment streams will follow the interference alignment criterion to maintain the optimal degrees of freedom (DoF) performance;the superposition streams are handled via successive interference cancellation at all the strongly interfered receivers to improve the overall achievable rate.The joint transceiver designs for SICA is modeled as a weighted sum rate(WSR)maximization problem,and then can be alternately solved for a local optimum according to the optimality equivalence between WSR and its corresponding weighted mean square error(WMMSE) problem.Simulation results have confirmed the sum rate improvement and DoF optimality of the proposed SICA scheme.

Keywords: interference alignment; successive interference cancellation; interference management; ultra dense networks

I.INTRODUCTION

To cope with the challenge of 1000 fold increase in mobile data traffic, the fifth generation (5G) has adopted nework densification as one of the key techniques to expand the wireless network capacity.Dense small cell networks and distributed antenna system,deployed in urban indoor and outdoor scenarios, will complement the macro cell coverage in edge areas and dead zones,and help offload mobile traffic from macro base stations [1].The indoor deployment is vital for 5G since 70-80 percent of mobile data traffic originates indoors[2].Indoor ultra dense small cell deployment enables flexible plug and play fashion, and can provide enormous improvement in both network spectral efficiency and energy efficiency.Accordingly,the operators’capital expenditures and operating expenses can be saved[3].Besides the dedicated indoor deployment, there are also outdoor-to-indoor and indoor-tooutdoor service provisioning strategies as the complements for indoor and outdoor users[4,5].In those deployment scenarios, the influence of path loss resulting from in-building penetration can not be ignored.The in-building penetration loss includes the propagation attenuations through outer walls, interior walls,glass windows, and other obstructions.Especially in modern buildings,engineers tend to choose advanced construction materials to achieve thermal isolation and energy-efficiency goals, making the penetration loss 20-25dB higher than old buildings[6–8].

The influences of penetration loss on interference links or desired links are different.If added only on the interference links,the penetration loss will weaken the interference power,and thus bring about better isolation between receivers.It has been confirmed in[9]and[10]that the wall loss would shield small cell users (SUE) from the interference of macro cells and other small cells,and increase the admitted SUE number and indoor throughputs.Thus the penetration loss has a positive impact on indoor interference mitigation.However,the situation is more complicated when the desired link experiences penetration loss.First,since the penetration loss will weaken the desired signal power, extra link budget should be considered to guarantee the target user’s quality of service, or the SUE may switch to another access point (AP) with better direct link quality.This is reasonable since one SUE usually attaches to the AP with the lowest path loss.Second,the penetration loss can cause unidirectional strong interference to some receivers.Considering one indoor ultra dense small cell deployment scenario where multiple APs are deployed on the ceilings of rooms and corridors, the indoor AP will be under saturated traffic load if multiple users in the same room are requesting for service simultaneously.Thus, one indoor SUE may seek for access from outside-serving APs, including outdoor macro base stations, outdoor small cell APs, and indoor small cell APs deployed in neighbor rooms or corridors, if they can provide more satisfactory data rate than the nearest but overloaded indoor AP.Depending on whether attached to a outside-serving or outside AP,SUEs in the same room can be classified into two types: the outside-served SUE and the inside-served SUE.Since the transmitted signals from the outside-serving AP experience much more penetration loss than that from the inside-serving AP, the outside-served SUEs may suffer strong interference from the inside-serving AP, while the insideserved SUEs may receive relatively weak interference from the outside-serving AP.This kind of interference relationship can be described by theK-user interference channel (IC) model with partial unidirectional strong interference.Besides the indoor dense small cell deployment,the partial unidirectional strong interference may also exist in outdoor heterogeneous networks,due to the diverse transmit power levels of different kinds of APs and the link heterogeneity resulting from the irregular deployment of APs and users.

ForK= 2, in two-user interference channel,the capacities with different interference cases have been widely discussed[11].The unidirectional strong interference case in two-user IC is also called the mixed interference case; its currently known capacity achieving scheme is to decode interference when it is stronger than signal and to treat weak interference as noise [12, 13].The two-user IC with mixed interference is quite common in device to device(D2D),ad-hoc,and homogeneous/heterogeneous cellular networks.With successive interference cancellation (SIC), concurrent connections and network throughputs can be effectively increased in those network scenarios[14–18].However,for the generalKuser IC with partial unidirectional strong interference withK ≥3, the achievable capacity is more complicated.In theK-user interference channel IC, when all receivers experience moderate interference, interference alignment is the existing optimal transmission strategy to achieve the maximum degrees of freedom(DoF) [19, 20] .When strong interference exists, we naturally expect to benefit more from decoding the strong interference than from just aligning them,as the two-user IC with mixed interference does.

So far, there has been little work about how to deal with unidirectional strong interference in generalK-user IC.In [21] Huang H.and Vincent K.N.Lau considered decoding and removing strong interuser interferences,and those strong interference links can be treated as interference-free.Thus theK-user IC with some strong interference links can be transformed into the partially connected interference channel, the alignment feasibility constraints can be relaxed,and more transceiver pairs can communicate simultaneously [22–24] .However, considering practical deployments, the mutual strong interference case discussed in [21] is more common in D2D or ad-hoc networks but infrequent in cellular scenarios, since each user tends to access to its nearest AP.Instead,the partial unidirectional strong interference is more commonly seen in indoor and heterogeneous cellular networks, for example, an inside-serving AP and a macro BS may generate unidirectional strong interference to outside-served UEs and SUEs, respectively.Another important but unconsidered problem is the achievable rate from the strong interference link.Since one strong interference signal should be decoded successfully at its desired receiver and all the strongly interfered receivers, its achievable rate is naturally limited by the minimum decodable rate at all those receivers involved.This constraint determines how much rate gain we can benefit from the strong interference,and should be taken into consideration in designing the transmission strategy.Recently some works have focused on combing IA and SIC to suppress interference in single cell broadcast channels, homogeneous/heterogeneous multicell interfering broadcast channels, and cognitive networks [25–28].Those works usually choose users with different path losses to form multiple clusters, and utilize SIC to enhance the achievable sum rate of cluster users.The application of SIC in cluster users, also called the Non-Orthogonal Multiple Access (NOMA), has been widely discussed in single cell broadcast or access channels when the users’pathlosses differ significantly[29,30].Thus,IA are usually adopted to cancel inter-cell and inter-cluster interference, while SIC handles the intra-cell or intra-cluster interference.In those works,SIC deals with the superposition of user signals within the same cluster, rather than the strong interference from different clusters, and therefore the unidirectional strong interference between APs are not considered.Motivated by those,this paper aims at integrating the advantages of SIC and IA to design new transmission schemes appropriate for the practical cellularK-user IC with partial unidirectional strong interference.

The main contributions of this paper are concluded as follows.First, we propose the Successive Interference Cancellation and Alignment (SICA) scheme in theK-user IC with partial unidirectional strong interference.In SICA,two types of data streams are transmitted simultaneously,i.e.,the alignment streams and the superposition streams.The alignment streams follow the IA design criterion to guarantee the overall DoF;the additional superposition streams,sent by the strong interference source transmitter,are handled via successive interference cancellation at all strongly interfered receivers.Next, the joint transceiver design for SICA is modeled as a weighted sum rate (WSR)maximization problem,and then the optimality equivalence condition between WSR and its corresponding weighted mean square error(WMMSE)problem is derived, based on which the original WSR problem can be alternately optimized for the local optimum solution.Finally, we use simulation to confirm the effectiveness of the proposed SICA scheme to find its dominant region.

The remainder of this paper is organized as follows.The system model is presented in Section II, and the SICA scheme is discussed in Section III.Section IV shows and interprets the simulation results, and Section V concludes the paper.

Notice that in the following notations,normal letters denote scalar values, boldface lowercase letters and boldface uppercase letters separately represent vectors and matrices.AHdenotes the conjugate transpose operator for matrix A.

II.SYSTEM MODEL

Let us consider theK-user IC model with partial unidirectional strong interference shown as Figure 1,whereKtransmitters send independent data simultaneously to their corresponding receivers, generating non-ignorable interference with each other.Specifically, one transmitter generates strong interference to the other receivers,labelled in red in Figure 1.As discussed previously, this scenario is common in dense indoor small cell network and outdoor heterogeneous networks.One possible practical deployment case is illustrated in Figure 2,where UE 1 is the inside-served SUE and the other users are all outside-served SUEs.

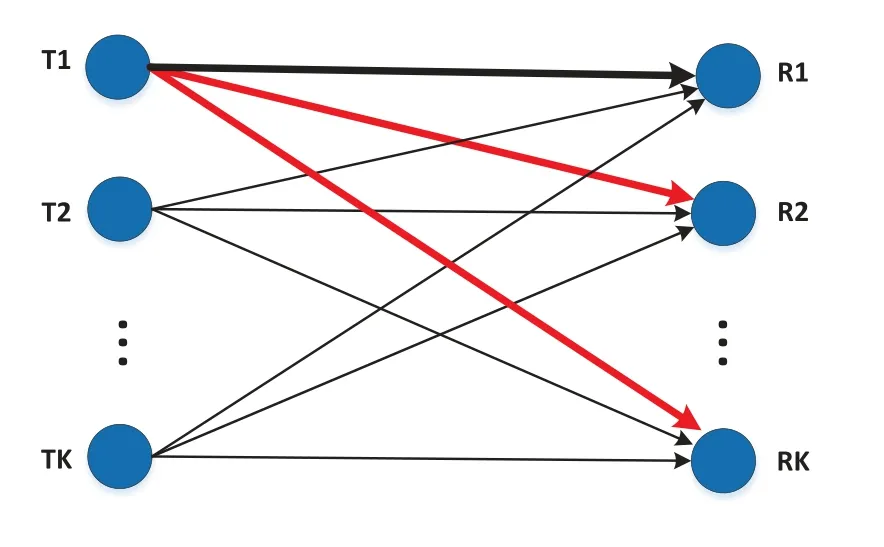
Figure 1. K-user IC with partial unidirectional strong interference from T1.

Figure 2. Practical indoor deployment scenario for 4-user IC with partial unidirectional strong interference.

The transmitters and their desired receivers are denoted byT1,T2,...,TKandR1,R2,...,RK, respectively.All transmitters and receivers are separately equipped withMandNomnidirectional antennas.TransmitterTisendsdidata streams to receiverRi.Thus the received signal vector atRkcan be written as

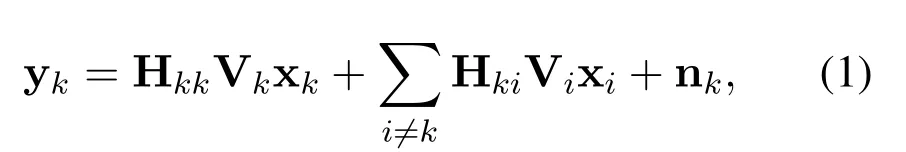
For generality,we assumeT1causes strong interference to the other receivers,Lk1=1, andLki <1 for1.The magnitude ofLkiindicates how much the penetration loss has weaken the signals for the outsideserved SUEs, and also represents the extent to whichT1strongly interferesRkfor1.

III.TRANSCEIVER DESIGN IN SUCCESSIVE INTERFERENCE CANCELLATION AND ALIGNMENT SCHEME

In this section, we propose the joint transceiver design of SICA, including the fundamental principle,weighted sum rate maximization modeling,feasibility condition and iterative solutions.

3.1 Weighted Sum Rate Maximization for SICA

In the classicK-user interference channel model,symmetrical interference links are usually taken into consideration.However,in practical scenarios,the inbuilding penetration loss and the heterogeneous transmit power levels from different kinds of APs will exacerbate the interference links’asymmetry and heterogeneity.In the classic two-user IC with mixed interference,SIC has been utilized to combat the strong interference and increase the throughput.In a similar manner,we also design to benefit from the strong interference relationship.Besides,the DoF region ofK-user IC should be achieved.Thus, on the basis of fundamental interference alignment,the strong interference source,T1, can be assigned with extra superposition streams,which is decoded in priority and cancelled at its strongly interfered receivers.After the superposition streams are removed, the left alignment streams will still follow the alignment criterion.

ForT1,we separately denote the precoding matrices for the superposition streams and alignment streams as P1∈CM×dsand V1∈CM×d,wheredsanddare the numbers of the superposition streams and alignment streams,respectively.Thus the received signal expression atRkcan be rewritten as

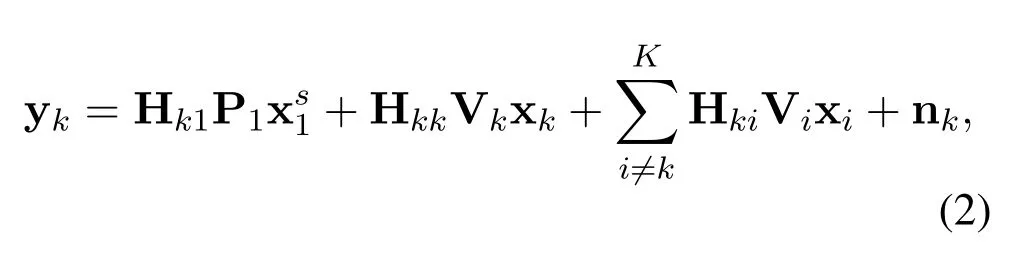
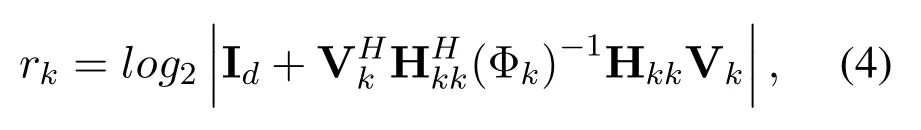
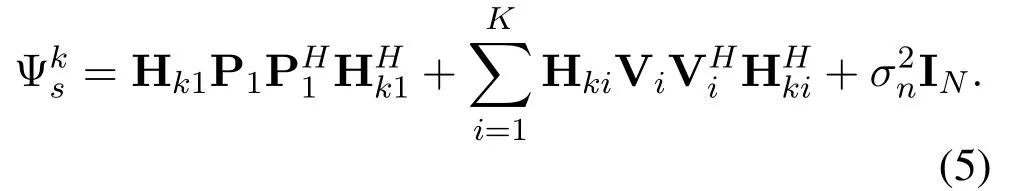
Then the corresponding MSE matrix ofatRkis denoted by

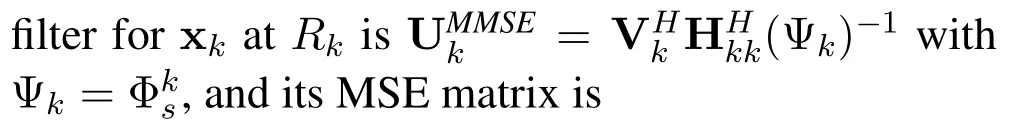
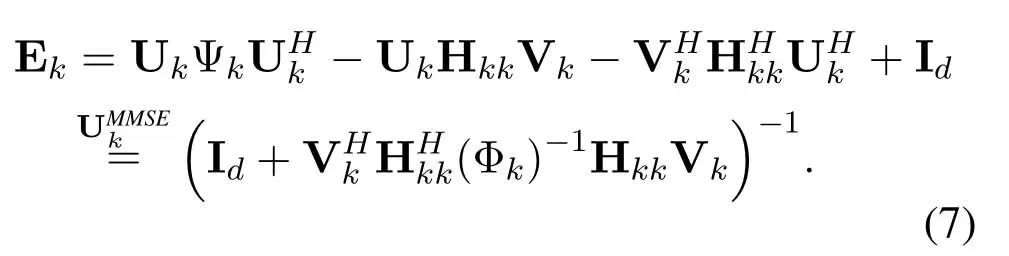
Thusrkcan be rewritten as

The optimal precoding and decoding matrix design in SICA can be modelled as the corresponding WSR problem in(8)

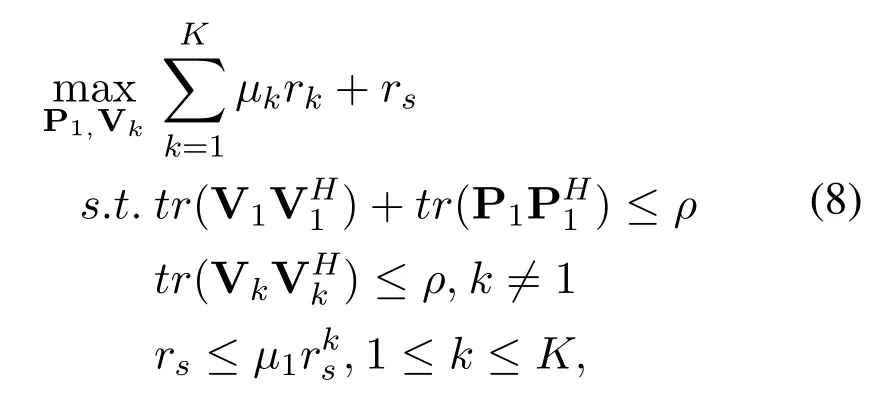
whereµkis the rate weight forTk.WSR is already known as NP-hard problem and difficult to obtain the global optimal solution[31].An alternative approach is to solve its corresponding WMMSE problem for local optimums.The optimality equivalence of WSR and WMMSE problems has been proved in broadcast channels (BC), interfering broadcast channels (IBC)and generalK-user IC [32–34].Similarly, we reveal that the optimality equivalence relationship is also applicable in SICA.

3.2 Optimality Equivalence Between WSR and WMMSE

The WMMSE problem corresponding to(8)is formulated as

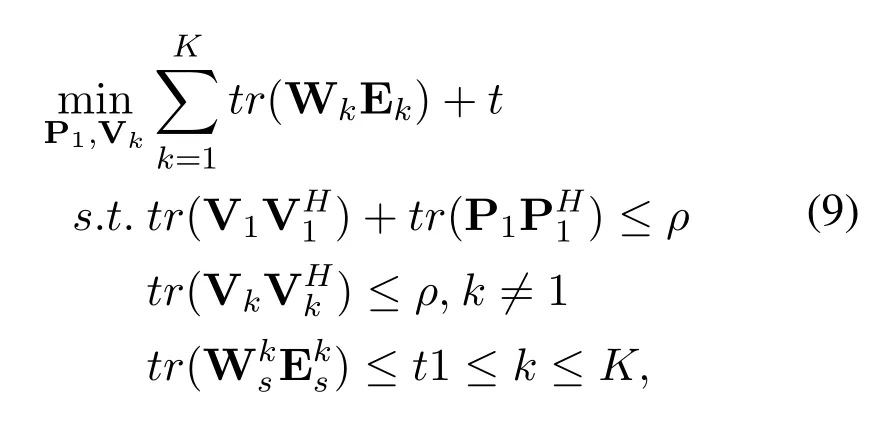
where Wk ∈Cd×dand∈Cds×dsare the weight matrices associated with xkandatRk,respectively.

The Lagrange functions of WSR problem (8) and WMMSE problem (9) are separately written as (10)and (11).

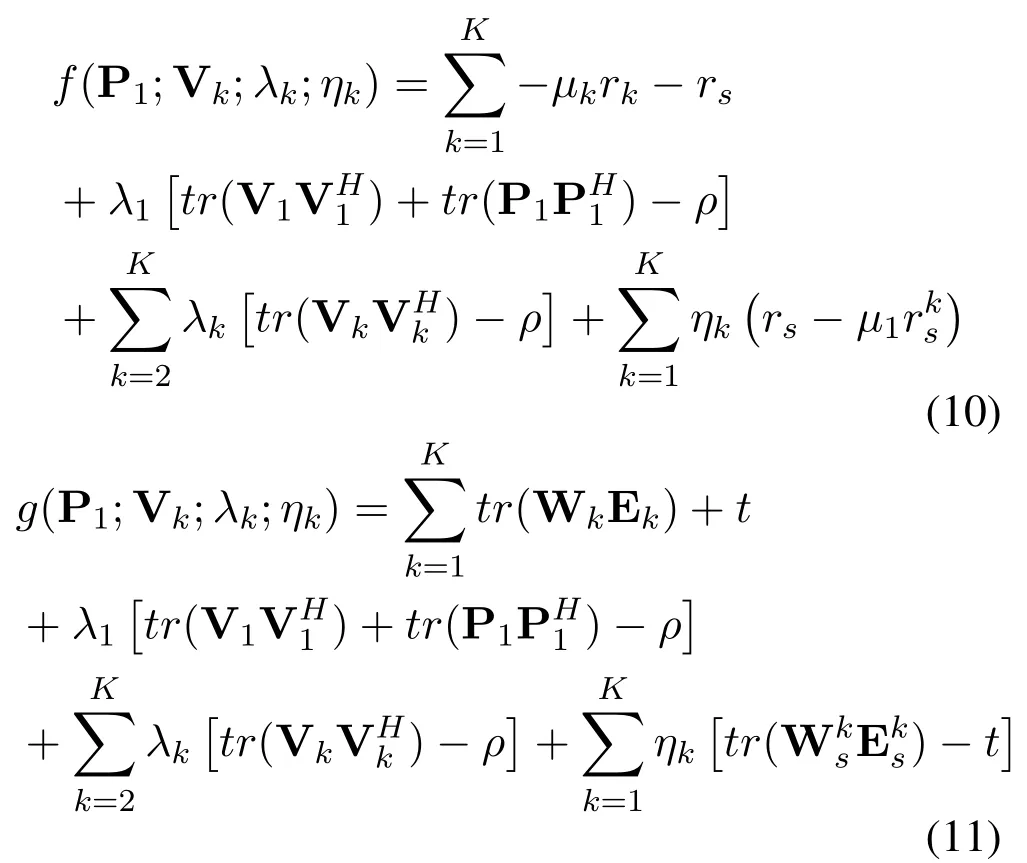
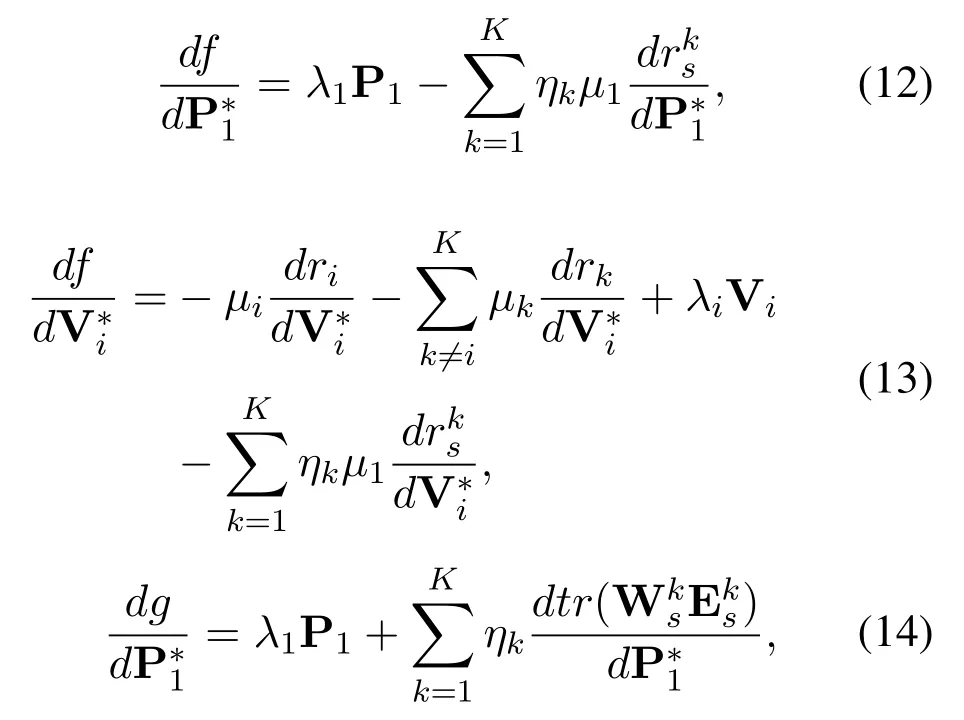
and

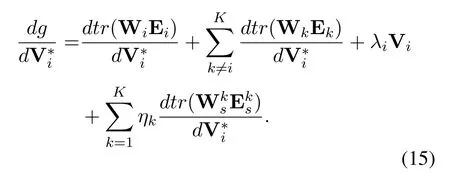
3.3 Alternating Optimization for WMMSE

Though the WMMSE problem(9)is still non-convex,we can reach a local optimal solution by alternately optimizing the precoding and decoding matrices.According to the expression ofin (6),is in the quadratic form of Qk,Vkand P1.Therefore,thoughtr()is not jointly convex on Qkand P1,it is separately convex on Qkand{P1,Vk}.In the same way,tr(Ek)is separately convex on Ukand Vk[35].

Treating Qkas constants,we can rewritetr(in the second order cone format of{P1,Vk}as Eq.(16)

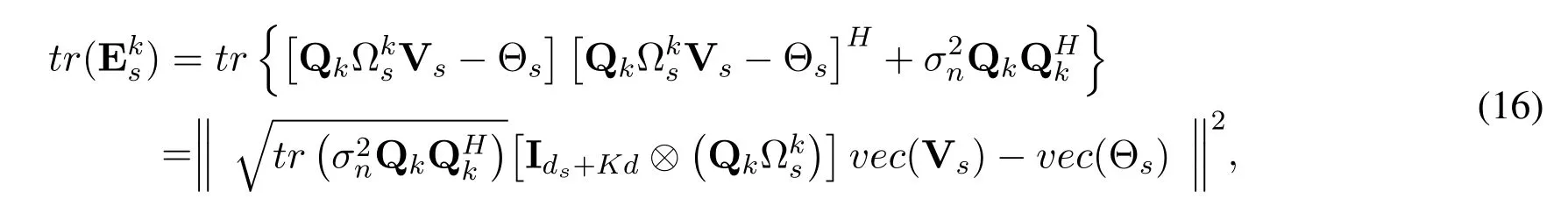
With Uktreated as constants,tr(Ek)can be rewritten in the second order cone format of Vkas Eq.(17)

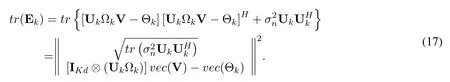
In (17), Ωk= [Hk1,Hk2,...,Hkk,...,HkK],

Therefore, the WMMSE problem with known decoding matrices Qkand Ukcan be rewritten as Eq.(18)with auxiliary variableslk,1≤k ≤K,landy.

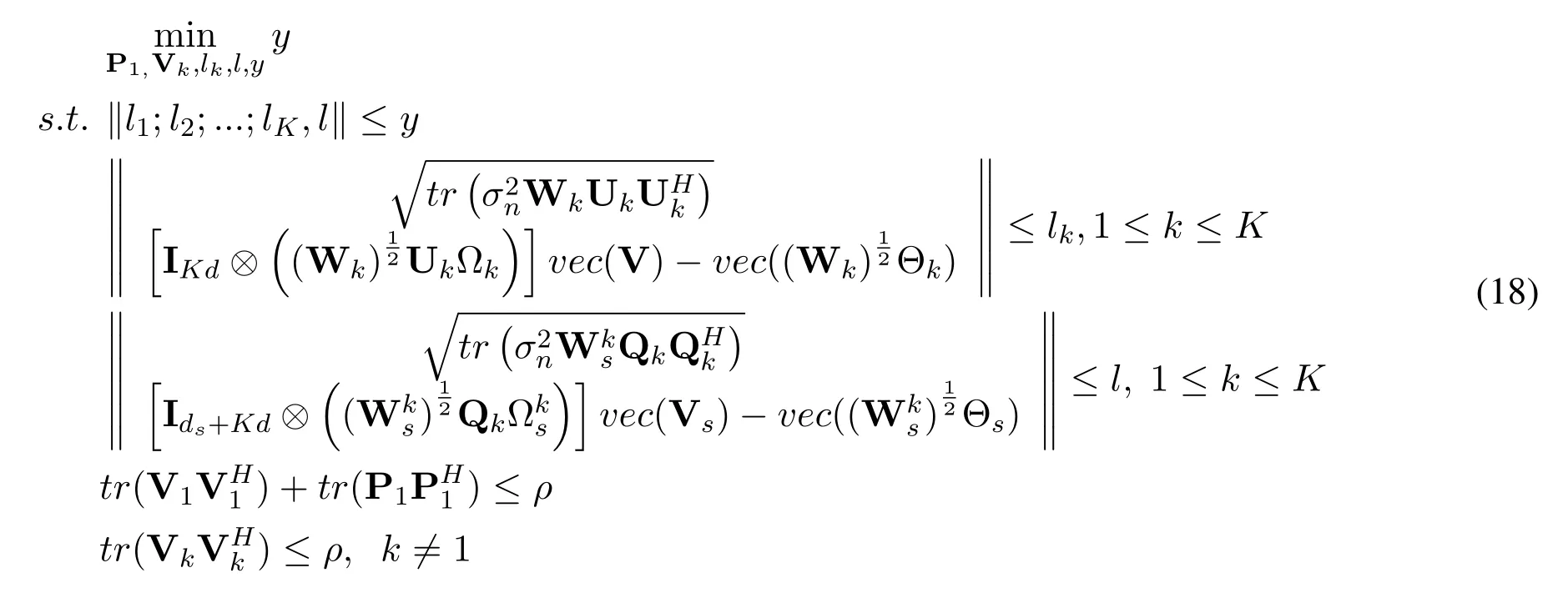
Equation (18) is a second-order cone optimization problem, and can be efficiently solved by some convex solvers,like CVX.Based on the optimality equivalence condition between WSR and WMMSE, the weight matrices Wkandcan be iteratively updated.

The detailed iterative SICA algorithm based on a sequence of WMMSE problems is given as follows.In the initialization step, Vk(0) is from the distributed interference alignment (DIA) algorithms in [36], and P1(0)is set to be orthogonal to V1(0).

3.4 Convergence Analysis

Here the brief proof of SICA’s convergence is given by reference to the convergence analysis in[31].Consider the two new cost functions Eq.(19)and Eq.(20),

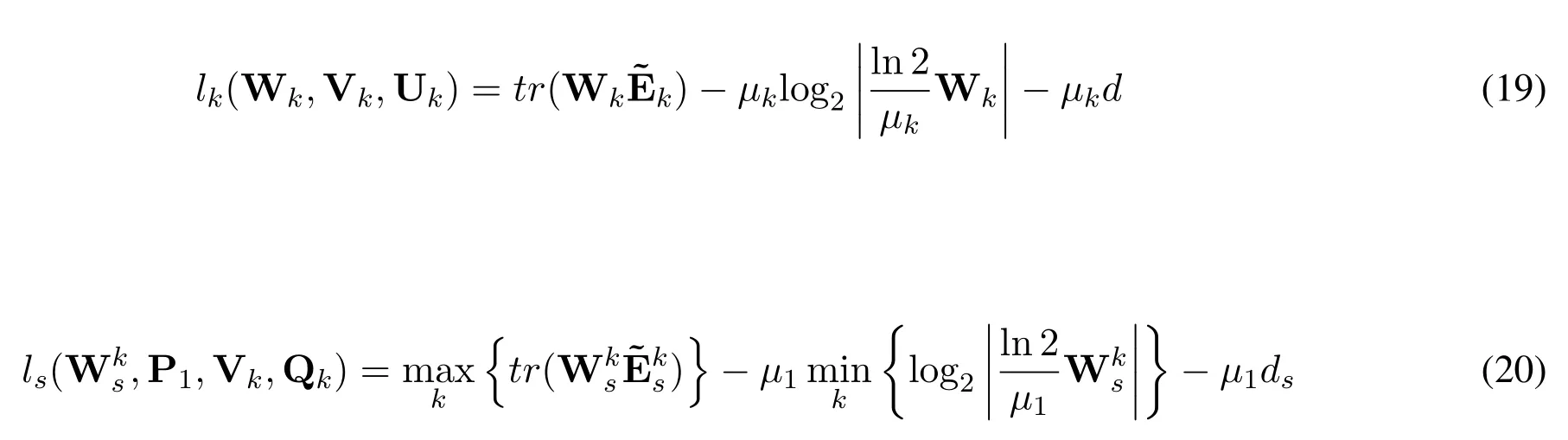
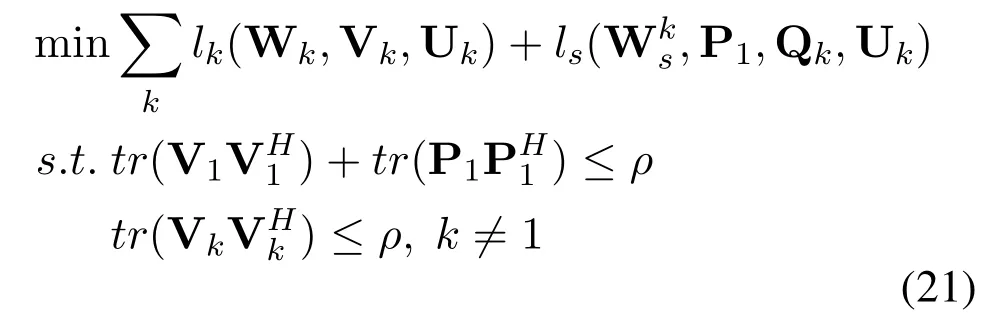
3.5 Computational Complexity

?

whereεis the algorithm precision of interior-point methods.

IV.NUMERICAL RESULTS

In this section, numerical results are presented to evaluate the proposed SICA’s sum rate performance by monte carlo simulation.We evaluate the performance of SICA in three typical cases,i.e.,(2×2,1)3,(3×2,1)4 and(3×3,1)5.All noise covariances are normalized,σ2=1;all transmitters have the identical normalized transmit power levelρ.The penetration lossLki=PLfori1 simulates the extent of the interference heterogeneity in those scenarios.We focus on the sum rate performance with equal weighting factorµk= 1,and then the basic principles are applicable to general weight settings.The detailed parameter settings involved in the simulation are illustrated in Table 1.

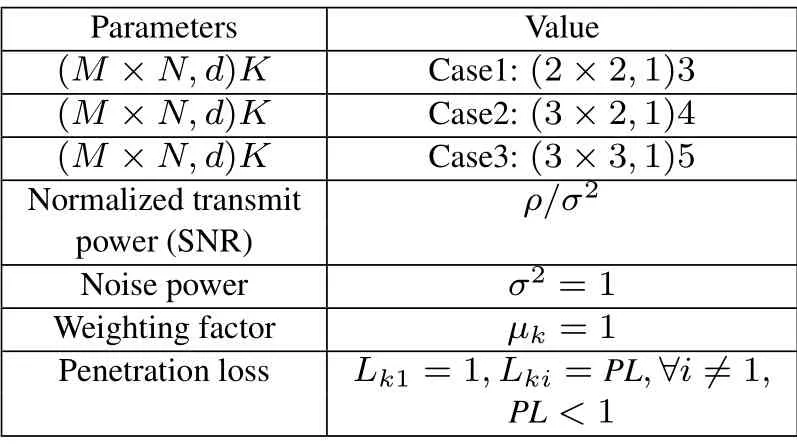
Table 1. Simulation parameter configuration.

4.1 Convergence Performance

At first,we examine the convergence properties of the proposed iterative algorithms.The iteration convergence results of one channel realization for weighted sum rate (WSR) and SICA in case (3×2,1)4 are shown in Figure 3.The WSR algorithm is from [33]with no superposition streams,and the two algorithms all adopt the same initial Vk(0) from the distributed IA(DIA)algorithm in[36].The normalized transmit power and pathloss are separately set asρ/σ2=30dB andPL=-20dB.From Figure 3, WSR and SICA can converge to their local optimums, and SICA achieves better local optimums than WSR.The influence of different initial iteration steps on convergence is also compared.Generally the more iterations in DIA, the higher converge speed those three algorithms have.Considering that a convex problems is solved in each iteration step of those three algorithms, it is preferable to prepare enough iterations of DIA to determine the initial point.As a result, we can significantly reduce the computation complexity and also guarantee the DoF performance in high SNR regime.

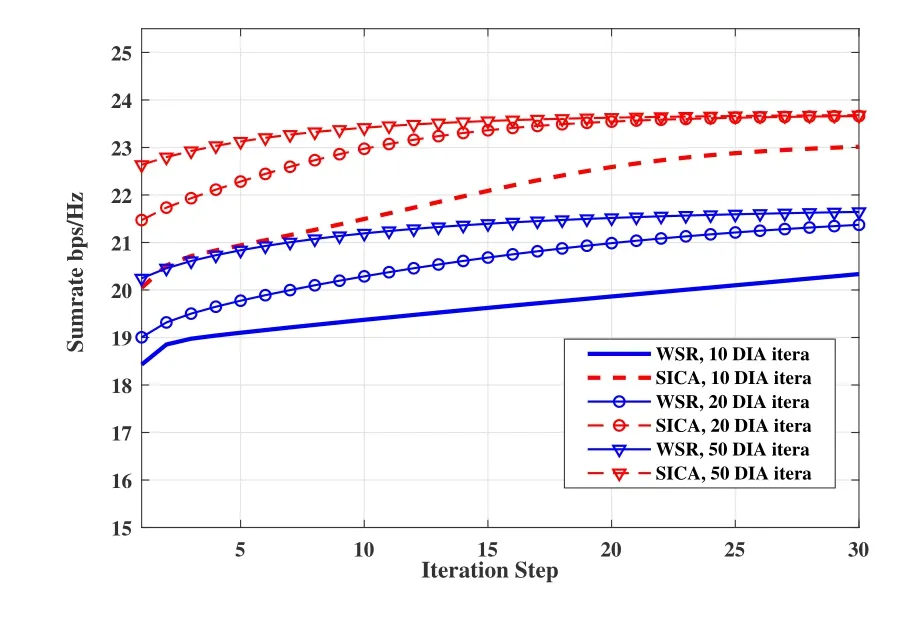
Figure 3. Convergence performance of WSR,and SICA in(3×2,1)4,ρ/σ2=30dB,PL=-20dB.

4.2 Sum Rate Performance

In this subsection we compare the sum rate of SICA with existing transmission strategies like DIA, WSR,single user (SU)-MIMO and multiple user (MU)-MIMO.The average achievable sum rates of SUMIMO,DIA,WSR,and SICA in(2×2,1)3 with different pathloss values are plotted in Figure 4-7.The sum rate of each transmission strategy with given SNR and PL is the average performance from 1000 snapshots.In each snapshot,the Rayleigh fading channelsare randomly generated according toCN(0,1),and then the achievable rate for a transmission strategy under each channel realization is calculated.In SU-MIMO, all receivers follow a TDMA rule to accessT1, and two data streams are sent.In DIA and WSR,each transmitter sends one data stream.As for SICA, four data streams are sent simultaneously, including three alignment streams and one superposition stream.DIA runs enough iteration steps to guarantee its DoF performance at high power level.In addition,DIA’s result is taken as the initial point for WSR and SICA.

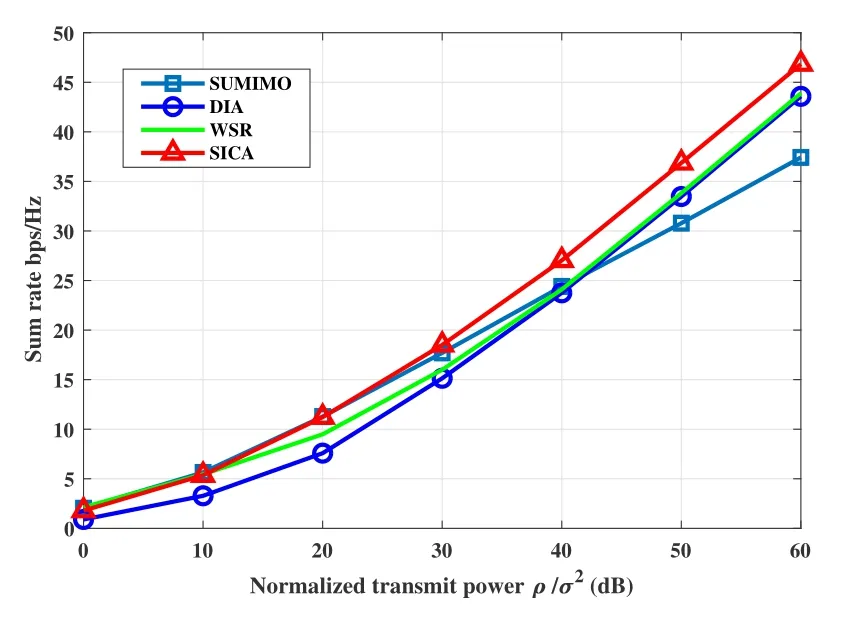
Figure 4. Sum rate performance of different transmission strategies in(2×2,1)3,PL=-20dB.

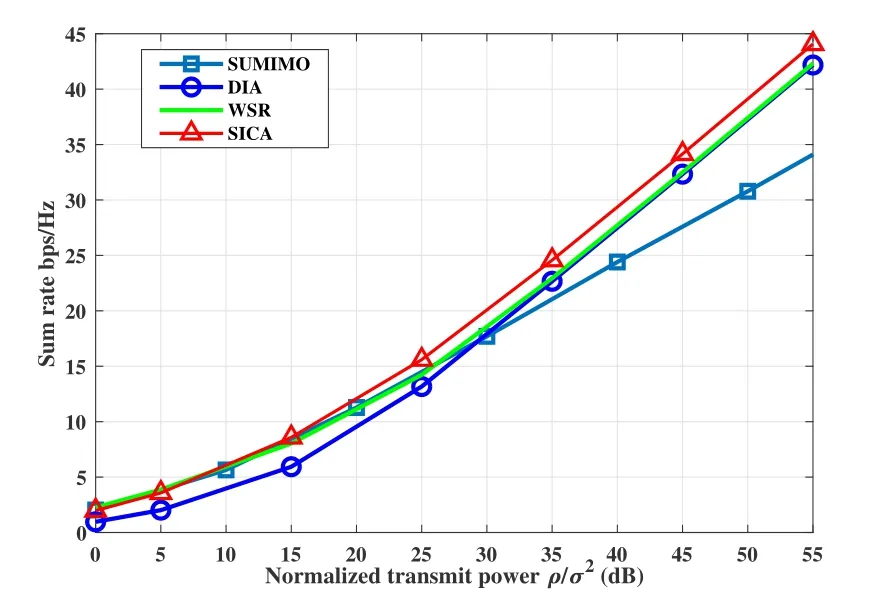
Figure 5. Sum rate performance of different transmission strategies in(2×2,1)3,PL=-15dB.

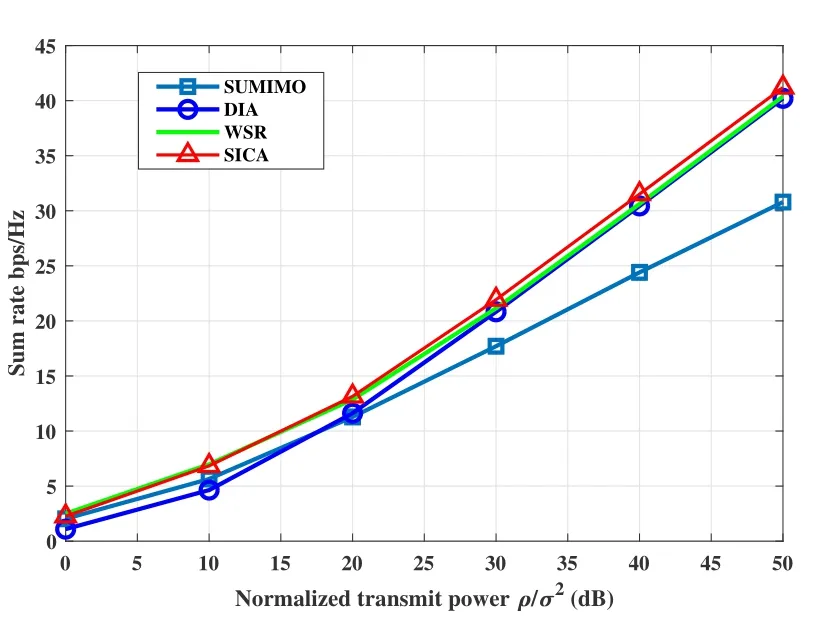
Figure 6. Sum rate performance of different transmission strategies in(2×2,1)3,PL=-10dB..

Figure 7. Sum rate performance of different transmission strategies in case(3×2,1)4,PL=-20dB.

Figure 4 shows the sum rate performance of case(2×2,1)3 withPL=-20dB.Among those existing transmission strategies,SU-MIMO achieves the highest sum rate during the SNR range of 0-40dB, while WSR and DIA outperform SU-MIMO when SNR is above 40dB.Though DIA and WSR transmit one more data stream than SU-MIMO, their DOF advantage is not obvious when the transmit power is not large enough,since two of the alignment streams are sent to the outside-served users with extra propagation loss.WSR and DIA begins to exceed SU-MIMO with SNR higher than 40dB.Nevertheless, the proposed SICA can hold the dominant position almost in the whole SNR regime, benefiting from the extra rate from the superposition stream.Moreover,SICA still obtains the same DoF as WSR and DIA in high SNR regime.The sum rate performances of (2×2,1)3 with otherPLvalues are shown in Figure 5 and Figure 6.With the decrease of|PL|, on one hand WSR and DIA gradually expand their dominant SNR regime compared with SU-MIMO, but on the other hand the sum rate gain of SICA gradually shrinks.In summary,for case(2×2,1)3 with partial unidirectional strong interference, we can directly adopt SICA as the universal transmission scheme in the whole SNR regime,without considering the critical point among other candidates.

Figure 7 compares the sum rates of SU-MIMO,MU-MIMO,DIA,WSR,and SICA in case(3×2,1)4 withPL=-20dB.Different from case (2×2,1)3, the transmitters and receivers have asymmetric antenna numbers,and thus MU-MIMO can be utilized.In the simulation, the MU-MIMO follows the zero forcing criterion in [39], and three data streams are simultaneously transmitted.In Figure 7, SICA also outperforms both SU-MIMO and WSR among the whole SNR regime.Since the slope of rate plot indicates the DoF at high power region,it can be seen that the DoFs of SU-MIMO and MU-MIMO are separately two and three while the DoFs of DIA, WSR, SICA and SICA all are four.Though having higher DoF,SICA’s rate is still inferior to MU-MIMO for SNR lower than 55dB,which is the critical point between SICA and MUMIMO.

The sum rate comparisons of candidate transmission strategies in case(3×3,1)5 are shown in Figure 8 withPL=-20dB.Similar to case(2×2,1)3,SICA achieves both the optimal DoF and sum rate in the whole SNR regime.Combining those comparisons, we can conclude that MU-MIMO is vital for cases with unequal transceiver antenna configuration,especially when the transmit power is not high enough.Due to the inbuilding propagation loss, in low to medium SNR regime, the sum rate performance depends largely on the achievable rate of the strong interference source transmitterT1.In SICA,the total number of the superposition streams and alignment streams sent byT1is limited by the receiver antenna number,while in MUMIMO the sent stream number equals to the transmit antenna number.Therefore,when the antenna number of transmitters is larger,MU-MIMO is more effective at low to medium SNR regime.The sum rate and DOF performance of SICA is more remarkable with high enough SNR and symmetric transceiver antennas.

Figure 8. Sum rate performance of different transmission strategies in case(3×3,1)5,PL=-20dB..

Figure 9 plots the sum rate gain of SICA over WSR in different cases to demonstrate how much we can benefit from the superposition stream rate.With fixed link heterogeneity valuePL, the sum rate gain increases with the transmit power at first and then remains almost constant.Obviously, more sum rate increment will result from stronger partial interference.The sum rate gain from the superposition stream is also influenced by the transceiver antenna settings.If the sum DoF is fixed,the symmetric antenna case generally achieves more rate improvement than the asymmetric antenna case.

Figure 9. Sum rate gain of SICA over WSR in different cases.

V.CONCLUSION

In this paper, we aimed at theK-user IC with partial unidirectional strong interference, and designed new transmission strategy SICA,which combines the principles of IA and SIC to cope with moderate interference and strong interference, respectively.Besides utilizing alignment streams,SICA supports additional superposition streams which are treated as strong desired signal or strong interference and dealt with SIC.The coexistence of these two streams can not only enhances the achievable sum rate when significant link heterogeneity exists,but also achieve the optimal DoF as IA.Therefore,SICA is suitable for indoor small cell network and heterogeneous network scenarios where strong inter-user interference exists with high probability.The WSR optimization problem was used to model the joint transceiver designs in SICA, and was alternatingly optimized by solving a sequence of equivalent WMMSE problems for a local optimum.Simulation results showed that SICA achieves better sum rate performance than existing WSR, DIA and SU-MIMO schemes especially in equal transceiver antenna cases.

ACKNOWLEDGEMENT

This work was supported by the National Natural Science Foundation of China(62101415)and the Guangdong Basic and Applied Basic Research Foundation(2020A1515110757).