基于改进分水岭算法的结核感染T 细胞菌斑检测

吕铭轩，陈兆学

（上海理工大学 医疗器械与食品学院，上海 200093）

0 引言

结核病是因机体感染结核分枝杆菌所引起的一种慢性传染病。据统计，中国每年因结核病死亡的人数高达13 万。因此，对结核病潜伏期感染的诊断以及防治工作十分重要。研究表明，结核感染T 细胞检测，对结核病具有较低的不确定性和良好的特异性，是近年来国内外结核感染诊断的一种可靠方法。该方法中，T 细胞斑点数量是诊断患者是否结核感染的依据，快速且准确地检测出菌斑数量是临床研究的一个重点和难点问题。随着计算机技术高速发展和图像处理技术日趋成熟，利用计算机自动计数来取代耗时长、效率低的传统人工计数已是大势所趋。

针对于此，研究人员提出了各种菌落自动分割和计数算法。如：Mohammad I Shah提出了一种基于分水岭分割的细菌自动检测和分类方法，在分水岭分割之前加入预处理技术，用于去除大于或小于细菌的伪影和干扰目标，最终对结核阳性图像细菌检测的灵敏度和精确度达到90.3%和77%。桑艳艳等提出了一种针对菌落图像改进的分水岭分割算法。在分割之前先对图像进行倒角距离变换和形态学处理，再利用区域合并算法聚集图像相似区域，很好地抑制了分水岭算法的过分割现象。张力新等提出了一种基于改进水平集的全自动菌落分割计数方法。该方法利用偏置场对背景建模来消除背景灰度的不均匀性，并构造了多相水平集算法，实现菌落目标的自适应分割。虽然以上算法在各自的实验对象上都取得了不错的分割效果，但由于在T细胞斑点试验中，形成的不同菌斑区域之间的灰度及形状大小往往会存在很大差异，而当前已有的菌斑自动计数算法大多是针对特定类型的菌斑图像进行研究的，针对性较强但鲁棒性差，难以对T 细胞菌斑图像实现自适应和精准的分割。

为解决T 细胞粘连菌斑图像的分割和计数问题，本文设计了一种基于改进分水岭算法的全自动T 细胞菌斑分割的计数算法。

1 算法流程

在T 细胞斑点试验中，抗原刺激诱导的斑点特征是清晰的深色圆点，实际计数应忽略小的及不清晰的斑点，仅对清晰的斑点进行计数。图1 所示为人工计数的6 组样例。

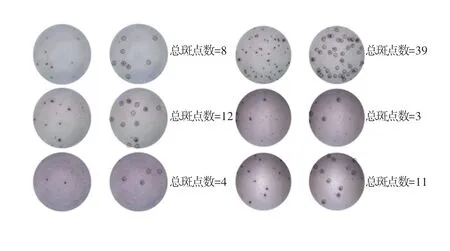
图1 计数规则示例图Fig.1 Example diagram of counting rules

根据T 细胞菌斑图像的特点和相关计数规定，本文设计的改进分水岭分割方法的过程主要包括以下3个基本步骤：

（1）预处理：包括消除背景和对图像进行滤波降噪，主要目的是去除无效区域和噪声干扰，增强图像质量。

（2）粘连区域识别：通过阈值分割、形态学处理和面积滤波等方法，找出图像中的大面积菌斑区域。

（3）分割计数：将图像分为大面积菌斑区域和小面积菌斑区域，利用标记分水岭算法分别对两类区域进行分割，合并分割结果并统计连通域数目得到最终计数结果。系统整体流程如图2 所示。

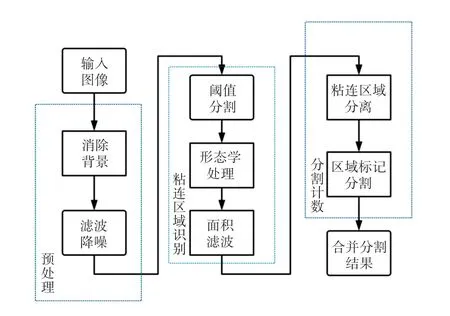
图2 T 细胞菌斑图像自动分割和计数算法流程Fig.2 Algorithm flow for automatic segmentation and counting of T cell plaque images

2 算法实现

2.1 消除背景

原始菌斑图像如图3（a）所示。原始菌斑图像常包含环境背景，如显微设备光源对细胞图像的镜像反射部分及其干扰区域。为了避免这些因素对图像处理的影响，同时减少计算负担、提高算法效率，需先将目标培养皿识别并提取出来。本文使用霍夫变换提取出培养皿区域，消除背景干扰。霍夫变换是图像处理中常用的检测算法，能够从较大的噪声环境中提取出图像里具有某种相同特征的几何形状（如直线、圆等）。本文基于霍夫变换实现圆形图像目标检测方法实现原理为：首先对原始图像进行二值化处理，通过边缘检测获取图像边界点。如果图像中存在圆形，那么圆的轮廓一定属于边界点。圆的边缘点的一般表达式为：

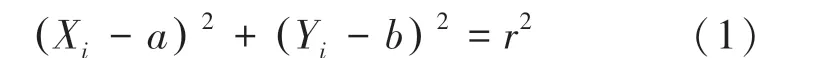
其中，（，）为圆心，（X，Y）为圆上的点，即待检测圆所对应边界点。

若转换一下视角，把（X，Y）看成圆心坐标，（，）理论上当对应以各边缘点为圆心、半径为的一系列圆的公共交点。因为数字图像中圆形表达的误差和边界点检测误差的存在，各圆之交点实际上分布在以（，）点为中心的一个小区域中，而半径也有微小误差。因此，霍夫变换常常首先限定一个包含圆心坐标的二维区域，基于枚举其中（，）组合，并针对所有边缘点（X，Y）依照式（1）进行计算，对所得的在预估的（，，）参数空间中的对应位置进行投票，最后选取得票数最多的（，，）参数组合，作为图像中所检测到的圆的参数。本文基于该方法可以确定培养皿所对应圆的圆心和半径参数，进而获得有效的培养皿区域。经霍夫变换得到的结果如图3（b）所示。

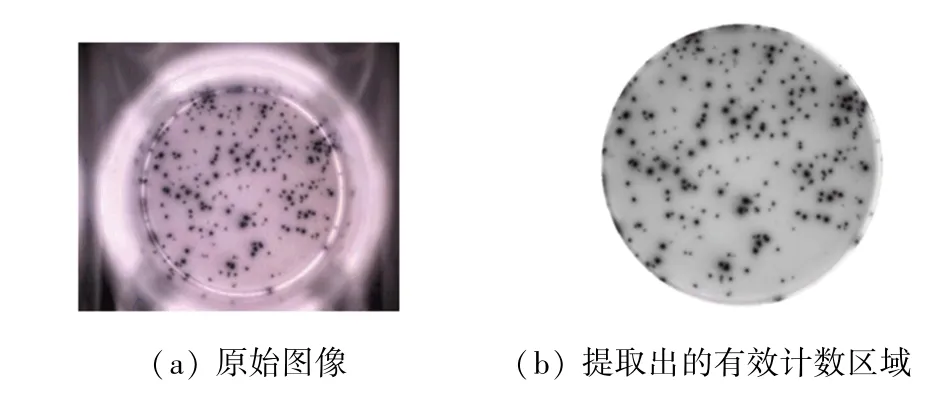
图3 原始图像和提取出的有效计数区域Fig.3 Original image and extracted effective counting area

2.2 滤波降噪

通过滤波处理，消除图像数据中可能存在的一些噪声污染。本文分别使用均值滤波、中值滤波、双边滤波对图像进行处理。通过实验对比发现：均值滤波处理后的菌斑图像会变模糊，会导致后续的粘连菌斑的识别非常困难。双边滤波计算量较大，实验中取到的原始菌斑图像大小均为3 288×4 608，因此耗时过长。中值滤波在平滑脉冲噪声方面有很好的去噪效果，同时还保留了图像的尖锐边缘，但可能会将图像中的细小菌斑当成噪声误处理掉，而本文中T 细胞菌斑计数任务要求忽略小的斑点，正好将此缺点转换成了优势。因此中值滤波非常适合本论文算法的处理要求。图4 分别是均值滤波和中值滤波处理后的结果。从中可以看出，与均值滤波相比，中值滤波结果的对比度更好。

图4 滤波效果的比较Fig.4 Comparison of filtering effects

2.3 二值化

把灰度图像转化为二值图像时，通常是设定一个灰度阈值，根据图像中每个像素点的灰度是否达到该阈值，来判断该点属于背景区域还是目标区域。其公式如下：

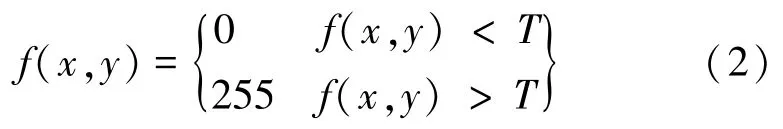
其中，是设定的阈值，确定合适的值是达到好的分割效果的关键。

二值分割常用的方法是最大类间方差（Qstu）法，直接使用该方法得到的效果如图5（a）所示。可以看到，部分背景区域被划分到了目标区域，尤其是菌斑粘连的区域，轮廓失真较为严重，这与培养皿图像中包含大量灰度与背景十分接近的菌斑区域相关。因此，对于本文研究的菌斑图像，单一阈值的分割效果往往不尽人意，若采用局部阈值算法，则计算量又过大。为此，本文根据菌斑图像的特点，使用一种改进的阈值解决该问题，其具体算法是：把最大类间方差法得到的二值化图像看成一个掩膜，与原图像相乘，得到不含菌斑的背景部分；计算背景部分的平均灰度得到阈值，再基于阈值得到最后的二值化结果。本文算法的处理结果图5（b）所示，可见其分割效果得到了明显改善。

图5 二值化效果图对比Fig.5 Comparison of binarization effect diagrams

2.4 传统分水岭算法

本次研究使用分水岭算法对图像进行分割，该算法的思想源自于地形学，其原理是把一幅图像视为跌宕起伏的地形曲面，采用浸水模型对图像进行分割。传统分水岭算法对细微边缘、噪声和细小的灰度变化敏感，将其直接用于梯度图像时，噪声和梯度的其它局部不规则性常常会导致过分割。解决该问题的一种方法是加入一个预处理阶段，将其他相关知识带到分割过程中，从而限制允许的区域数目。通过对标记符的控制来抑制过量分割区域的产生。具体实现方法分为以下几步：

第一步：对二值化处理后的图像进行欧氏距离变换，得到一副灰度图像；对该图像使用分水岭变换得到分，即标记背景标记。

第二步：利用扩展最小值变换，提取图像的局部极小值作为内部标记符。

第三步：利用强制最小技术产生梯度图像的局部最小值，对修改后的图像进行分水岭分割。完成分割后，采用四邻域标准遍历搜索图像连通域，标记排序每个连通域实现计数。

扩展最小值变换在Matlab 中可以直接调用函数（，）来实现。其中，是输入图像，为最小值变换的区域最小值，参数的选取会影响最终分割结果。图6 是直接使用标记分水岭算法分割后的部分区域结果，其中图6（a）参数设置为50，部分粘连区域的菌斑无法被准确分割出来，图6（b）参数设置10 时，产生了大量过分割现象。通过多次改变参数发现，由于T 细胞菌斑图像本身的特点，无论怎么改变参数，对全局进行一次性标记分水岭分割得到的结果均无法令人满意。

图6 传统分水岭算法处理后的部分区域Fig.6 Part of the area processed by the traditional watershed algorithm

2.5 改进分水岭算法

为了解决上述问题，本文结合形态学处理和面积滤波技术，对分水岭算法进行了改进。在分割前对图像进行粘连区域识别，并根据菌斑面积的大小，将图像分成两个部分。具体实现方法如下：

第一步：对二值化后的图像进行形态学处理。

第二步：对形态学处理后的图像进行连通域统计，设定一个面积阈值，根据菌斑面积的大小将图像分成两个区域。

第三步：分别对两个区域的图像进行分水岭分割，合并两幅图像得到最终分割结果。

利用形态学中最基本的膨胀和腐蚀运算，可以进一步对二值化图像进行处理，以改善分割效果。

膨胀运算公式为：

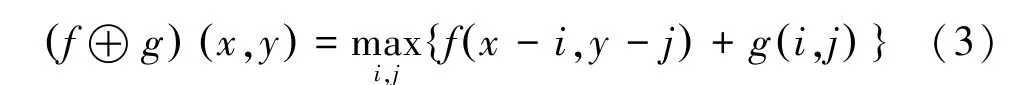
式中，为待处理图像，为结构元素。

图像被结构元素所膨胀，实际就是计算该点局部范围内各点与结构元素中对应点的灰度值相加，并选取最大值作为该点的膨胀结果。该运算可以起到边界点扩充和连接内部缝隙的作用。

腐蚀运算可以切断粘连对象间的细小连接，消除细小噪声，其运算公式为：

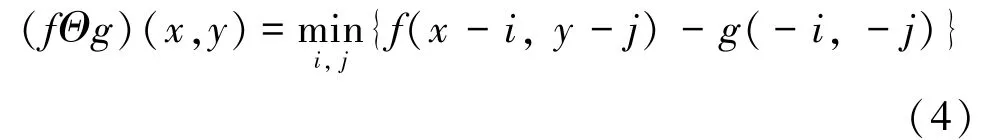
通过对这两种算法不同顺序的结合使用，以及对不同形状大小的结构元素的选取，可以扩展形态学图像处理。如图7 所示。

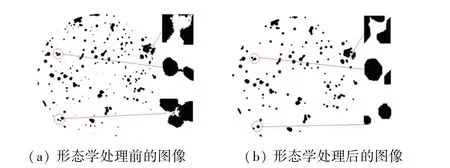
图7 形态学处理前后的对比图Fig.7 Comparison chart before and after morphological processing

图7（a）是形态学处理前的图像，从中选取了3处细节放大，由此可见图像中存在的问题：

（1）对象轮廓十分粗糙，整体存在很多杂质和噪声。

（2）对象间存在细小连接。

（3）对象内部有小孔洞。

图7（b）是选取半径为5的圆形结构元素，对图像进行先腐蚀再膨胀得到的结果。从局部放大图中可以看到，形态学处理可以让菌落轮廓变得光滑，同时剔除了一些杂质点和伪菌落。

对形态学处理后的图像进行连通域统计，并通过面积滤波删除小面积对象，将得到的新二值图像构成一个掩膜。将该掩膜与原图像相乘，并把其它部分置为背景灰度，得到图像的大面积菌斑区域。在这一过程中，本文设置的面积阈值为50，即像素点大于50的区域被视为大面积菌斑区域，该区域包含粘连菌斑，需要进一步进行二次分割提高计数精度。如图8 所示，图8（a）是大面积菌斑区域，包含了所有粘连菌斑。图8（b）是小面积菌斑区域，包含了所有满足计数条件的菌斑。

图8 大面积菌斑区域和小面积菌斑区域Fig.8 Large plaque area and small plaque area

使用改进后的算法得到结果如图9 所示，其中图9（a）是对图像的第一次分割，仅检测面积较小的菌斑区域，所有被检测出来的菌斑均用“+”符号标记。图9（b）是针对面积较大菌斑区域的二次分割。可以看出，粘连区域的菌斑被准确识别并用“.”符号标记出来。合并两次处理结果得到的最终效果如图10 所示。结果表明，本文算法能够精准的识别出粘连菌斑，同时能有效排除面积或灰度未达到计数规定的菌斑。

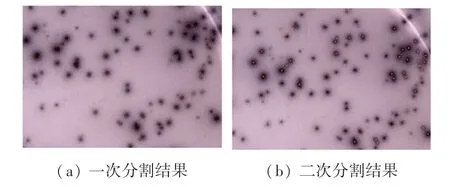
图9 本文算法处理后的部分区域Fig.9 Part of the area processed by the algorithm in this paper

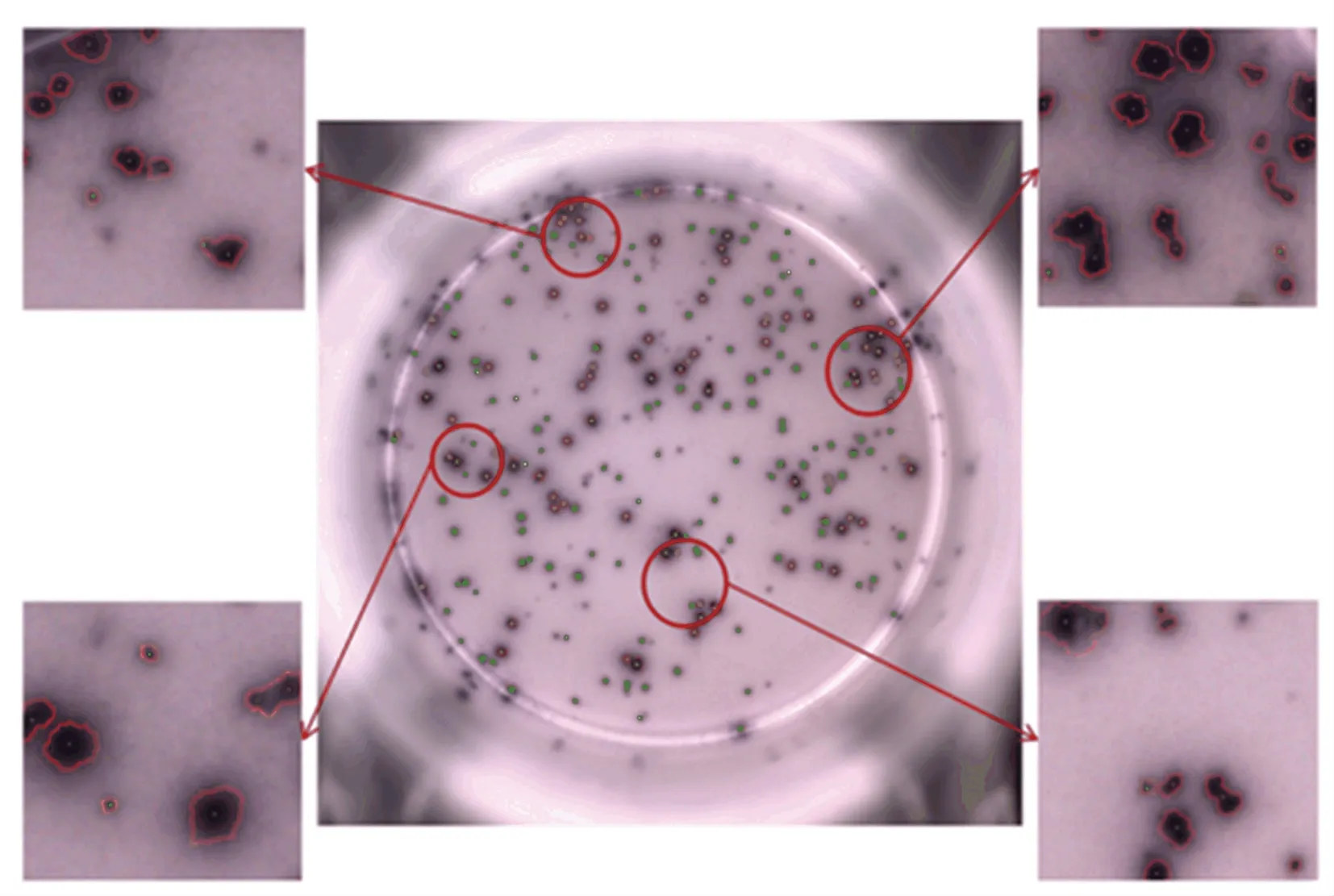
图10 本文算法最终结果Fig.10 The final result of the algorithm in this paper

3 实验结果分析

为了测试本文算法的有效性和稳定性，对复星医药集团股份公司提供的一组菌斑图像进行实验验证。实验选取的原始图片大小均为3 288×4 608；实验平台为window10、CPU 为AMD3900X、MATLAB版本为2019b。

通过与传统标记分水岭算法的计数结果以及人工计数结果进行比对，来验证本文算法的有效性。图11 是选取的4个具有代表性的菌斑样本的分割结果。其中，培养皿A 透光均匀，菌斑清晰可见且数量很少，几乎没有粘连现象，计数最为简单；培养皿B 存在部分粘连菌斑，总体菌落相对较清晰，是本次实验中最常见的一类图像；培养皿C 中的菌落分布比较密集，对于这一类图像，人工计数比较吃力；培养皿D 中的菌斑灰度非常不均匀，伪阴影过多且粘连现象太过严重，即使是肉眼也难以分辨。表1 是图11 中的计数结果以及对剩余50 多个菌斑样本计数的平均结果。其中，人工计数的结果是由10个人分别计数，去掉最大值和最小值取平均得到的。准确率由该算法得到的计数结果除以人工计数结果得到。

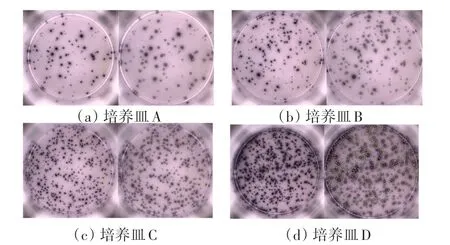
图11 培养皿图像的分割结果Fig.11 Select the segmentation results of four petri dish images

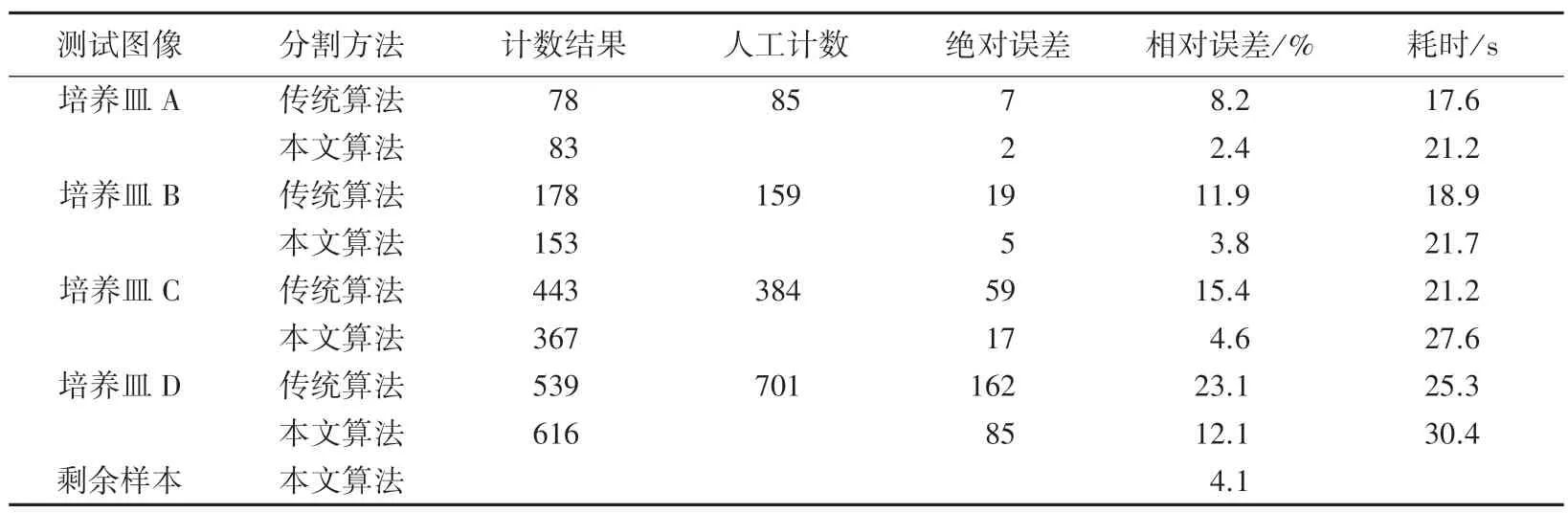
表1 结核感染T 细胞菌斑图像计数结果Tab.1 Results of image count of plaque of T cells infected by tuberculosis

实验结果表明，除了少量如培养皿D 这一类的菌斑图像（实际临床得到的这种图像通常都是斑点饱和的阳性对照，不需要准确计数。），本文的算法对结核感染T 细胞菌斑图像的检测准确率均在95%以上，耗时30 s 以内。相较于传统的标记分水岭算法，本文算法大大提高了计数精度。

4 结束语

本文根据T 细胞菌斑图像的特点，设计了一种基于改进分水岭算法的菌斑检测方法。在传统标记分水岭算法的基础上，加入了一个粘连区域识别的阶段，通过把图像分成两部分并分别分割，大大提高了分割精度，有效抑制了传统分水岭算法的过分割现象。实验证明，本文的算法满足T 细胞菌斑图像的计数要求，对T 细胞菌斑图像有良好的分割效果。由于本文算法只需稍作修改，因此也适用于其它具有类似特征的菌斑或细胞图像的分割，应用前景较广。