基于RBF-BP 神经网络的人居环境自然适宜性评价

彭义春，张捷，卢伟杰，陈佐瓒

（玉林师范学院 计算机科学与工程学院，广西 玉林 537000）

0 引言

人居环境的地形、气候、水文、植被等自然因素不仅影响人居自然环境的质量，而且决定着人居环境的自然适宜程度。人居环境自然适宜性综合评价是个高度非线性问题，人居环境自然因子与评价分级结果之间是一种较为复杂的非线性映射关系，要直接确定这种非线性关系并不简单，需通过各种经验方法进行各因子权重的计算。BP 神经网络因具有较强的学习能力和非线性拟合能力，已有学者实证应用于人居环境适宜性评价领域。如，杨东等采用BP 神经网络方法，对东营市三县两区的滩涂利用现状进行适宜性评价；朱振兴基于BP 神经网络构建了城市宜居性评价模型；范峻恺等基于熵值法确定的指标权重，构建BP 神经网络模型，对海绵城市建设的适宜性进行评价。本文提出并采用RBF-BP 神经网络完成评价指标权重的计算，实例表明该方法既充分利用了RBF 神经网络逼近速度快的优点，又具备BP 神经网络能较好预测未知样本的能力，提高了评价精度。

1 RBF-BP 神经网络模型

1.1 RBF-BP 神经网络结构

BP 神经网络和RBF 神经网络是两种常用的神经网络算法。BP 神经网络作为一种全局逼近网络，是一种稳定可靠的非线性函数逼近方法，但存在收敛速度慢、容易陷入局部极小值的缺点。该系统虽然存在训练不稳定、难以保证学习结果一定能达到均方误差的全局最小，但其具有良好的泛化性能。RBF 神经网络是一种最佳逼近网络，在隐含层存在足够多的神经元条件下，能以任意精度逼近任何连续非线性函数，具有训练简洁、学习收敛速度快和克服局部极小值问题等优点，但泛化能力较差。RBF-BP 神经网络综合了RBF 神经网络和BP 神经网络各自的优点，由RBF 子网和BP 子网组成。其中包括输入层、两个隐含层和输出层的4 层神经网络系统。其模型结构如图1 所示。

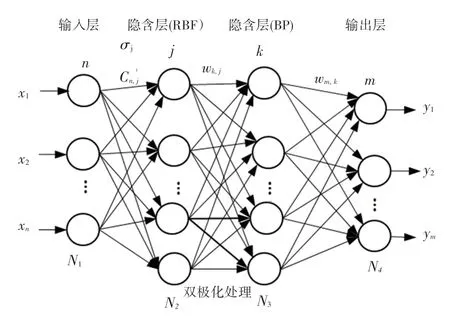
图1 RBF-BP 神经网络结构Fig.1 RBF-BP neural network structure

其中，、、和分别表示输入层、第一隐含层、第二隐含层和输出层的神经元个数； σ为函数宽度矩阵； C 为中心矢量矩阵； w 为第一隐含层到第二隐含层之间的权值矩阵； w 为第二隐含层到输出层之间的权值矩阵；第一隐含层神经元的激活函数为Gauss 型函数；第二隐含层神经元的激活函数为Sigmoid 型函数。

1.2 RBF-BP 神经网络算法设计

首先，根据输入的训练样本，通过RBF 子网初步训练，RBF 子网的隐含层节点对输入样本进行核映射后，需要先对核映射值进行双极化处理后方能作为BP 网络的输入，对φ（）双极化处理的公式为：

第一隐含层的输出（即为BPNN的输入）为：

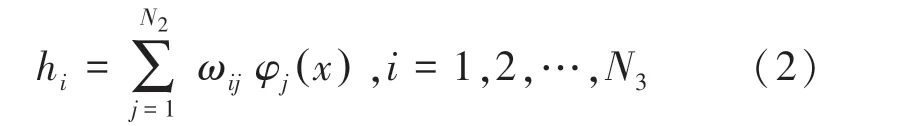
式中，为第二个隐含层（BP）节点个数， ω为两隐含层之间的权值。

然后，将RBF 子网的输出作为BP 子网的输入再进行加强训练；最后，BP 子网训练后得到结果，定量识别并输出结果。其算法流程如图2 所示。

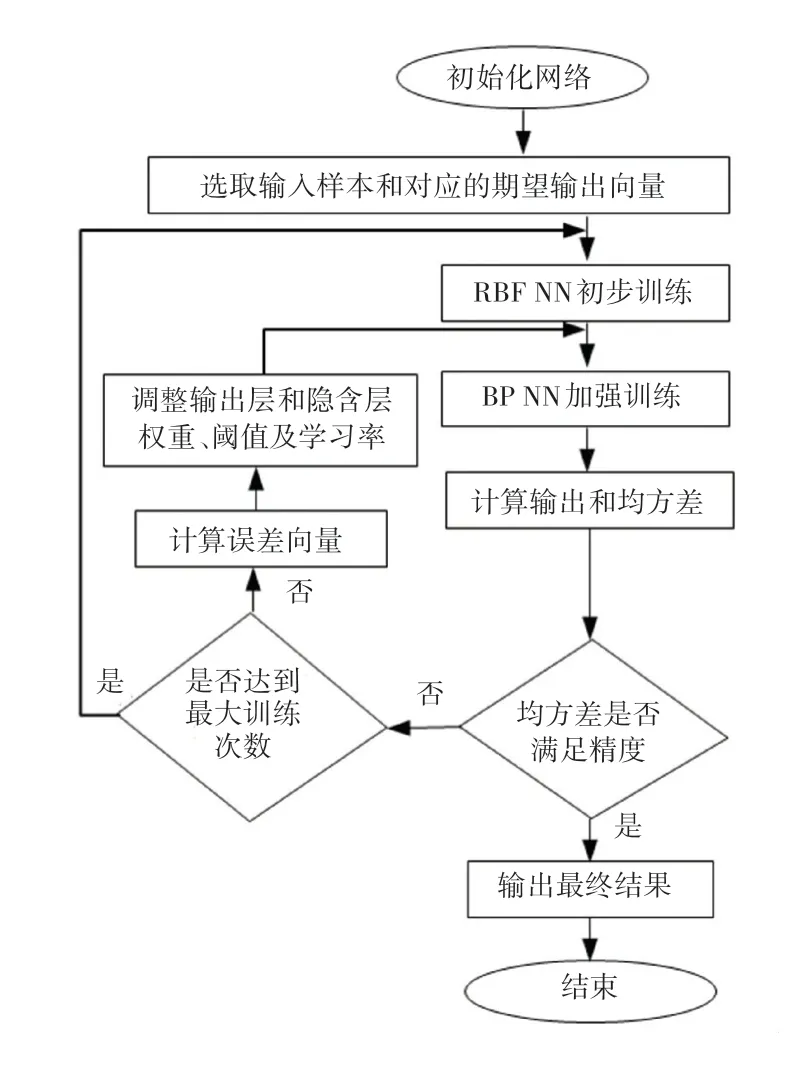
图2 RBF-BP 神经网络算法流程Fig.2 RBF-BP neural network algorithm flow

RBF-BP 算法实现详细步骤如下：

各层级的权值和阈值初始化，随机设为［0，1］间较小数，设置最大训练次数、目标精度和学习速率等参数。

计算中心向量，设置RBF 子网隐含层的传递函数为Gauss 型函数，其形式如下：

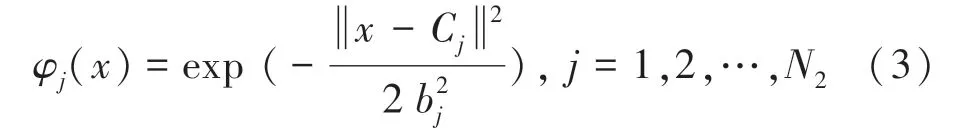
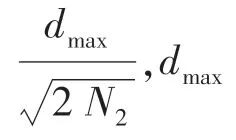
设置BP 子网隐含层的传递函数为Sigmoid 型函数：

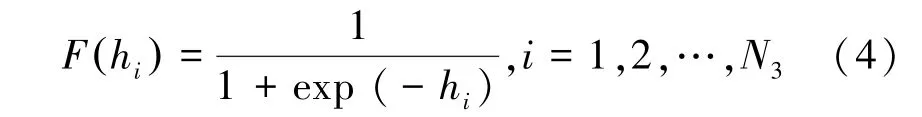
计算输出层节点的输出值。采用线性传输函数，其表达形式为：

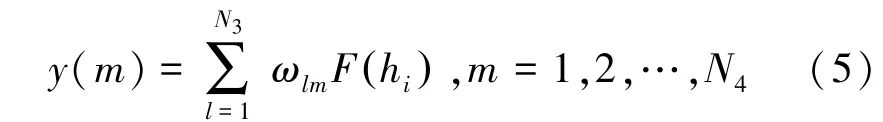
式中，（）为输出层第个节点的输出值；表示输出层个数；ω表示第二个隐含层神经元到输出层神经元间的连接权值。

计算输出层均方差：

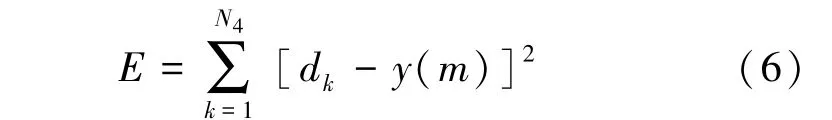
式中，d为期望的输出值。

计算输出层各神经元的误差向量：

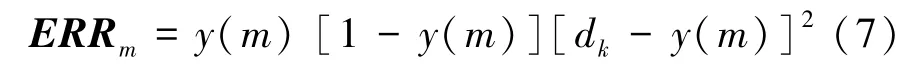
调整各层的权重、阈值和学习率：

按已知输出数据d与式（5）算出的输出数据（）之差来调整权重系数，调整量公式为：

式中：为学习速率（比例系数），可自适应调整，在计算中设定为属于［0，1］之间的值。在网络训练中如果能保证既不引起振荡又有较高的精度，可逐步提高值，直到满意的训练速度为止； x在隐层节点则为整个网络的输入，在输出节点中则为下层（隐含层）节点的输出（1，…，）；δ是一个与输出偏差相关的值。对于输出节点而言有：

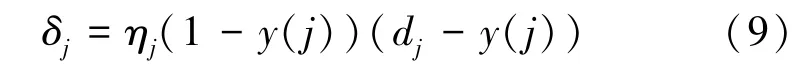
对于隐层节点而言，由于其输出无法进行比较.所以经过反向推算有：

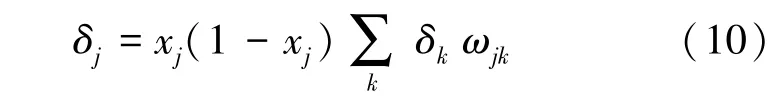
式中，指要把上层（输出层）节点遍历一遍，误差δ是从输出层反向逐层计算误差。

各层神经元的权值调整后为：

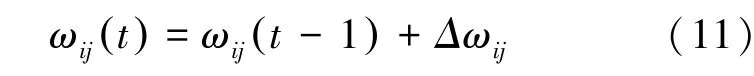
式中：为学习次数。

阈值调整公式为：

式中，表示学习速率。

在程序运行过程中，当RBF-BP 神经网络的训练误差小于所设置的目标精度时，则训练结束，此时处于收敛状态；当出现训练迭代次数大于设置的最大训练次数后，还未达到目标精度，网络结构不收敛，则重新返回到步骤2 继续执行程序，直至整个过程收敛。

2 实验与分析

2.1 数据来源

研究所需的数据主要包括两类：一是自然基础数据，包括东莞市的地形地貌、气候、水文和土地利用现状数据；二是人口密度和行政区划的空间数据。其中，2014～2020 年某个时间覆盖东莞市的Landsat 8 遥感影像，来自中国科学院遥感与数字地球研究所的对地观测数据共享计划服务网（http：／ ／ids.ceode.ac.cn／）；1：25 万DEM 数据、水域及行政区划等相关数据文件，分别来自广东省测绘局、东莞市税务局、东莞市测绘局；东莞市32个镇街的自动气象台站2014～2020 年逐月温度、降水、相对湿度、地面以上10 m 高度处的平均风速、日照时数等数据，来自于东莞市气象局；2014～2020 年人口数据来自于东莞市年鉴。

2.2 评价指标体系构建

本研究从指标体系的构成出发，将人居环境自然适宜性评价指标体系分为目标层、准则层、一级指标和二级指标层，见表1。

表1 人居环境适宜性评价指标体系构成Tab.1 The composition of the evaluation index system for the suitability of the human settlement environment

2.3 单因子评价指数计算

2.3.1 地形起伏度的提取

本研究采用窗口分析法，对1 ∶25 万的DEM 来提取东莞市地形起伏度，开辟1×1 km 大小的栅格区作为操作单元。利用ArcGIS 软件Spatial Analysis（空间分析）功能中的栅格Neighborhood Statistic（邻域统计）工具来实现；邻域统计以待计算栅格为中心，向其周围扩展一定范围，基于这些扩展栅格数据进行函数运算，从而得到此栅格的值。

根据封志明等人研究结果，将东莞市地形起伏度定义为：

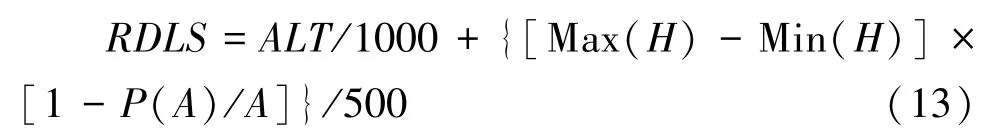
式中，为某一单元栅格为中心的一定区域内的平均海拔高度（m）；Max（）和Min（）分别为区域内的最高与最低海拔（m）；（）为区域内的平地面积（km）；为区域总面积（如本研究确定采用11 km 栅格为提取单元，则值为1 km。）；500 表示中国的中低山高度，即标准山高。

2.3.2 温湿指数计算

本研究采用温湿指数（Temperatuer-Humidity Index，THI）模型，来评测人居环境的气候适 宜性。的计算公式为：

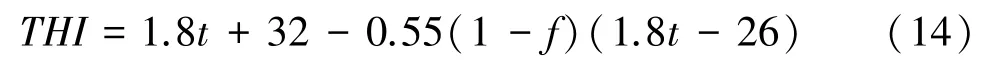
式中，为月均气温（℃），是月均空气相对湿度（%）。

运用ArcGIS的空间分析模块，以1×1 km 为基本研究单元，计算东莞市以及各镇街多年来12个月份的平均温湿指数。

2.3.3 水文指数计算

选取水文条件中的降水量和水域面积作为东莞市水文适宜性评价的指标。水文指数计算公式为：

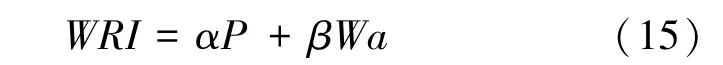
式中，为归一化的降水量，为归一化的水域面积。这两个归一化值均采用极差标准化得到，其取值范围为［0，1］，和分别为降水量与水域比例的权重。

本研究借用曲线回归方法，来确定权重系数和的值。以东莞市各镇街的人口密度为因变量，在SPSS 软件中分别以归一化的年均降水量和归一化的水域面积值为自变量，得到的拟合方程中，归一化年均降水量均值的系数为0.186，归一化的水域面积值的系数为0.046。即两个自变量的比值约为4 ∶1，所以系数和的值分别设定为08和02。

2.3.4 植被指数计算

植被指数通过土地覆被特征的指数和土地利用类型来表示。本研究运用如下模型求出东莞市的植被指数：

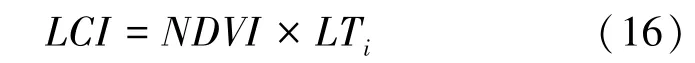
式中，为此单元的归一化植被指数，LT为各土地利用类型的权重。

通过专家打分、层次分析法，以及国家人口计划生育委员会制定的《国家人口发展功能区工作技术导则》和相关研究（文献［16-17］），得出土地利用类型6 大类中的25 类二级利用类型权重；然后，借助于ArcGIS 软件，将东莞市土地利用分类栅格数据转换为面数据，再在面数据上增加一个权重字段，按照表中字段计算，并对耕地、林地、草地、水域、建设用地和未利用地等6 大类土地利用类型的权重进行赋值，最后按权重字段将其转换为栅格数据集，得到土地利用类型权重栅格数据集。

2.4 基于RBF-BP 神经网络模型评价指标权重求解

2.4.1 综合评价模型

为了说明某一栅格单元或某区域的适宜性等级，根据上述研究的单因子对人居环境自然适宜性的贡献和影响不同，通过RBF-BP 神经网络计算每一评价因子对东莞市人居环境自然适宜性贡献程度的大小，再把4个归一化处理后的单因子指数的空间栅格数据进行空间加权叠加，计算得到人居环境自然适宜性栅格，然后分别按1×1 km 栅格和按行政区划进行综合评价，获得每个空间栅格数据和镇街的人居环境自然适宜性状况指数。其计算公式为：

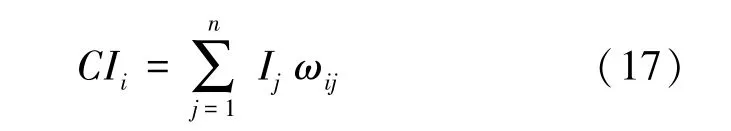
式中，I为第个评价因子的适宜性指数，ω为第个评价因子的权重。

根据相关文献和调研结果构建人居环境自然适宜性综合评价指数模型。人居环境自然适宜性评价指数的计算公式如下：

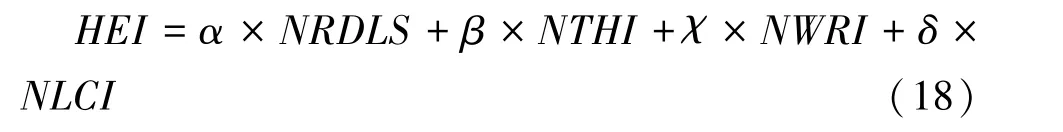
式中：为人居环境指数；为标准化地形起伏度；为标准化温湿指数；为标准化水文指数；为标准化植被指数；、、和分别为地形起伏度、温湿指数、水文指数和植被指数对应的权重。

2.4.2 RBF-BP 神经网络模型结构的确定

为了获得各评价指标的权重，需要对评价指标的值做标准化处理，对于逆向指标和适度指标还需做正向化处理，使得所有评价指标的值均介于［0，1］之间。正向指标采取最大效果法来实现标准化（式（19））；逆向指标采用最小效果法来实现标准化（式（20））；适度指标采用中心效果法来实现标准化（式（21））。

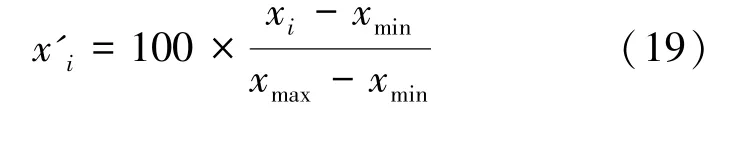
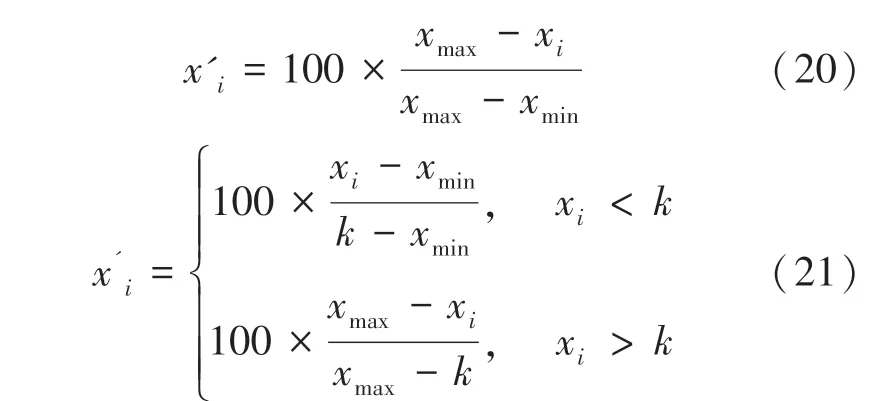
式中，x表示该指标的第个栅格的实际值；＇表示正向标准化后的值；为该因子最适度的值。

经标准化处理后，因子间则不存在量纲、数量级和变异程度的差异。之后，将标准化处理后的数据采用RBF-BP 神经网络模型求解每个单因子的权重。

首先，确定RBF-BP 神经网络每层神经元的数目，由于本研究中要求出4个单项指标的权重，则输入层和输出神经单元数均设为4。选取40 组数据作为神经网络的训练样本，10 组数据作为其检验样本。通过不断调试，依据输入层神经元数目＜隐含层的神经元数目≤输入层神经元数目+输出层神经元数目的原则，将第一隐含层和第二隐含层的神经元个数均设置为5。其网络结构如图3 所示。

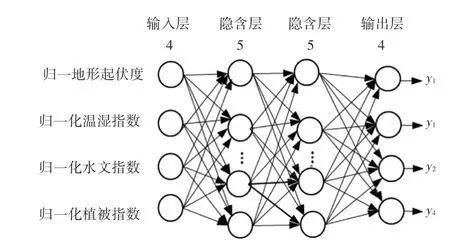
图3 RBF-BP 神经网络指标相关性求解模型Fig.3 Index correlation solving model based on RBF-BP neural network

第一隐含层的激活函数采用（）函数；第二隐含层的激活函数选用正切S 型传递函数（）；输出层神经元传递函数采用线性传递函数（）；网络训练算法采用LM 算法的（），学习函数采用梯度下降动量学习函数（）。

应用函数（）构建RBF-BP 网络：

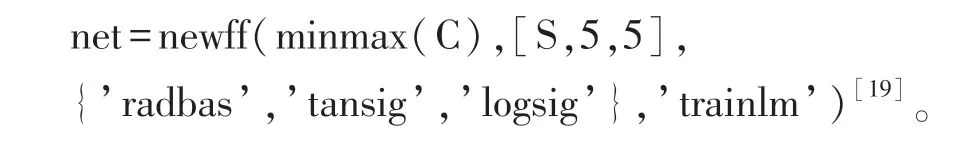
2.4.3 网络训练

按照图2的算法流程，在参数设定中，初始网络训练次数设定为100 次，误差阈值设定为0.000 01，学习速率设定为0.3，并采用模拟退火算法进行迭代调整。网络建立后，根据具体的应用和网络大小确定合适的样本数量对网络信号进行训练学习。按照1×1 km的栅格大小划分，将东莞划分为2 451个栅格。本研究通过建立评价指标特征和取值范围，选择1 500 组样本，各指标的属性值归一化处理后，得到的部分数据见表2。

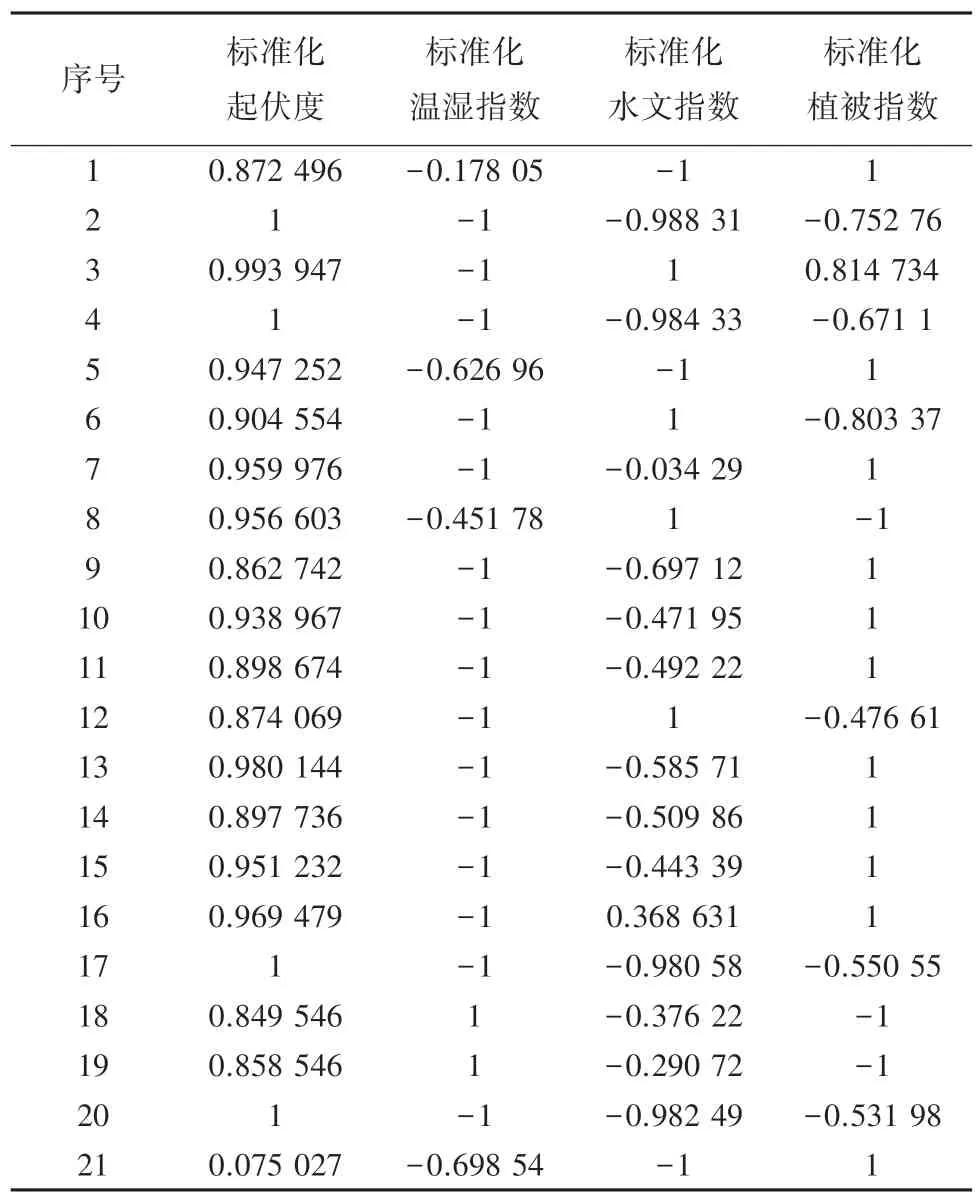
表2 样本数据Tab.2 Sample data

借助MATLAB 选择样本集中的40 组样本进行网络训练，训练最大循环次数为100。然后，再用全部样本进行测试。经网络反复训练发现，当迭代次数约达到29 次时网络趋于收敛，其收敛效果如图4所示。最后误差可达0.745 283×10。

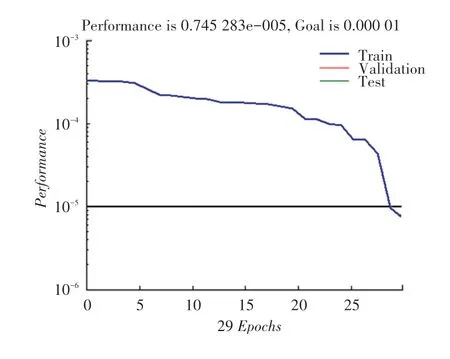
图4 网络的收敛图Fig.4 Convergence graph of network

2.4.4 模型训练结果分析

采用本文RBF-BP 神经网络模型对4个评价因子归一化数据的训练过程中，均方误差变化曲线如图5 所示，40 组测试样本的训练结果精度如图6所示。由图5 可见，BP 神经网络经过约55 次迭代达到收敛，而RBF-BP 神经网络模型约需29 次迭代即可达到收敛。由此可见，RBF-BP 神经网络不仅提高了收敛速度，均方误差也始终低于BP 神经网络，表明RBF-BP 神经网络能够提升模型的准确性。

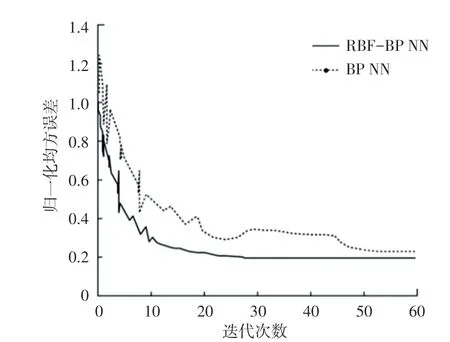
图5 归一化均方误差曲线Fig.5 Normalized mean square error curve

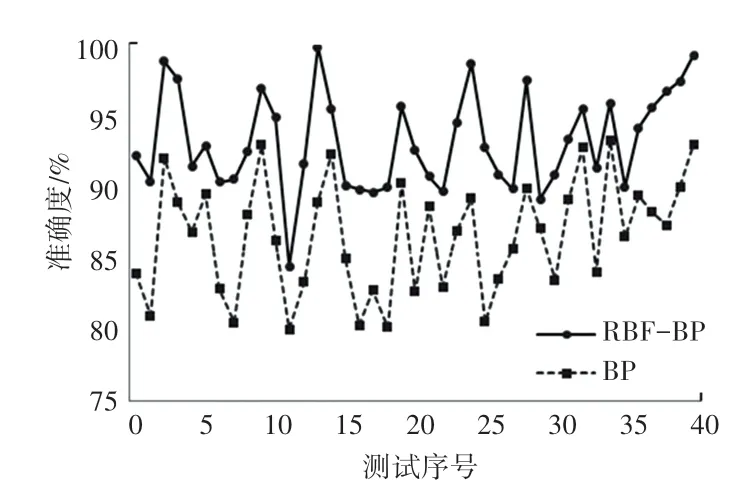
图6 准确度曲线Fig.6 Accuracy curve

图6 表明，虽然BPNN的评价精度较高（均高于80%），但RBF-BP 神经网络的评价精度要优于BP神经网络。统计结果表明，在40 组测试数据中，RBF-BP 神经网络模型训练结果准确度均大于89%，且其中23 组评价准确度大于92%，表明了模型具有很高的逼近精度。

2.4.5 指标权重的求解

神经网络训练的结果只是反映神经网络每个神经元之间的相关性，要想得到输入因子对输出因子的权重，还需进一步对各神经元之间的权重加以分析和处理。本文利用以下系数和指数来描述输入因子与输出因子之间的关系。

相关显著性系数：

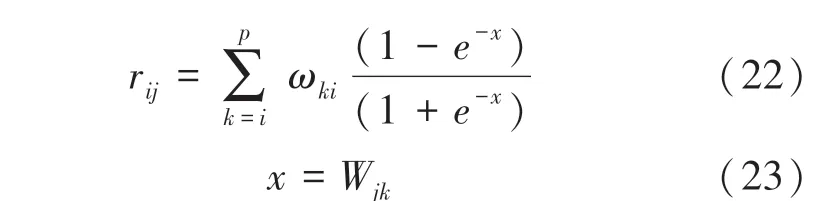
相关指数：

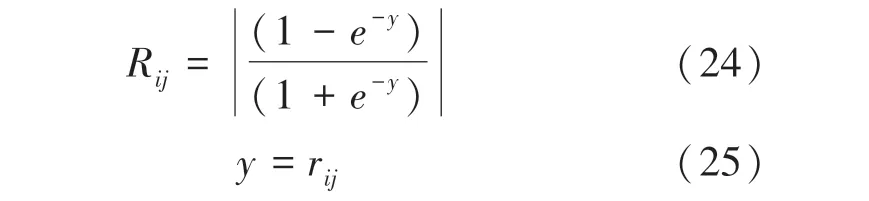
绝对影响系数：

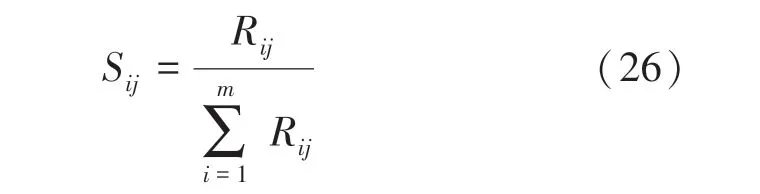
其中，为RBF-BP 神经网络输入单元，1，…，；为神经网络的隐含单元，1，…，；为神经网络的输出单元，1，…，；ω为输入层神经元和隐含层神经元之间的权重；ω为输出层神经元和隐含层神经元之同的权重。

以上3个相关系数中，绝对影响系数S表示输入层神经元到输出层神经元的权重。

运用公式（22）～公式（26）得出各评价指标的权重，见表3。

表3 评价因子权重Tab.3 Weight of evaluation factor

3 结果与分析

3.1 人居环境自然适宜性综合评价结果

通过ArcGIS的栅格计算，将RBF-BP 神经网络算法求出的4个因子权重（表3）代入到人居环境指数模型（式（18））中，以1×1 km 栅格为基本研究单元，计算可得东莞市人居环境指数。

东莞市的人居环境指数介于32.298 1～84.939 6之间，整体格局是中部和东部人居环境指数较高，往西和往南呈逐渐降低趋势。最低值在塘厦镇境内，最高值在清溪镇境内。参考已有划分方法（文献［18］、文献［21-23］），结合东莞市自然因子特征、人居环境指数范围，以及人口分布与自然环境的相关性，按人居环境指数从高到低将东莞市划分为Ⅰ～Ⅵ6个等级（分别对应：高度适宜区、一等比较适宜区、二等比较适宜区、一等一般适宜区、二等一般适宜区、临界适宜区），最后得出东莞市人居环境自然适宜性统计数据，见表4。

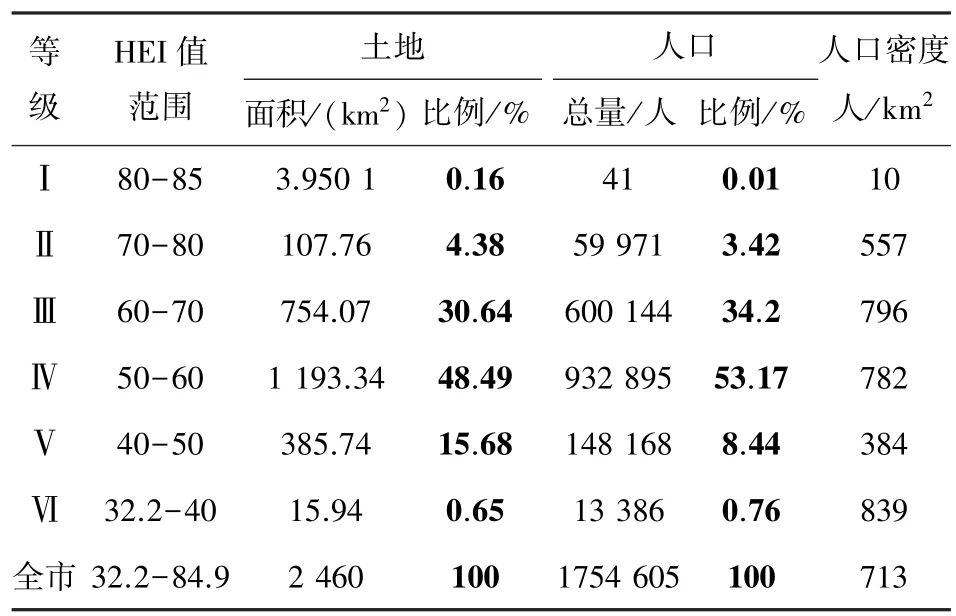
表4 东莞市人居环境自然适宜性评价结果Tab.4 Evaluation results of the natural suitability of the human settlement environment in Dongguan

从表4 可知，一等一般适宜区（Ⅲ）和二等比较适宜区（Ⅳ）面积最大，为1 947.42 km，占全市面积的79.13 %；其次为二等一般适宜区（Ⅴ），占全市面积的15.68%；高度适宜（Ⅰ）区占0.16%；临界适宜区（Ⅵ）占0.65%。一般适宜区面积最大、人口分布最多，面积达到1 579.09 km，占全市面积的64.17%；共有1 081 063人，占全市人口的61.61%；其次是比较适宜区，面积达到861.84 km，占全市面积的35.02%；共有660 115人，占全市人口的37.62%。

经统计数据结果，东莞市99.23%的人口生活在一般适宜区或比较适宜区，说明全市的人居环境自然适宜性程度适中，大部分地区地形、水文、植被等条件匹配较好，但总体适宜水平还有待进一步提高。

3.2 评价结果对比分析

为进一步测试RBF-BP 神经网络模型的评价性能，在实验数据不变的情况下，将其与文献［18］求出的4 项评价指标权重（0.33、0.32、0.16、0.19）代入HEI 评价模型，计算得到东莞市人居环境指数，进行性能对比测试。在IBM的SPSS 软件中，对两者的评价结果与人口密度，分别采用Pearson 相关性分析和Kendall的tau_b、Spearman的rho 相关系数分析，结果见表5、表6。从表中可得，本文模型较文献［18］的相关性更为显著，说明评价结果较为理想。

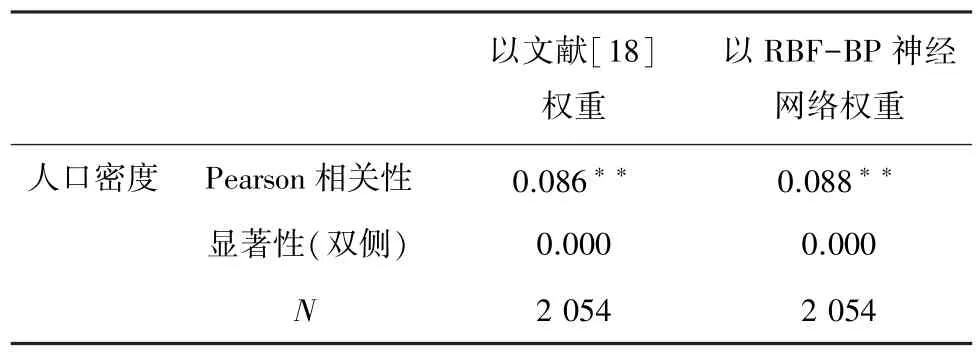
表5 Pearson 相关性比较Tab.5 Comparison of Pearson correlation

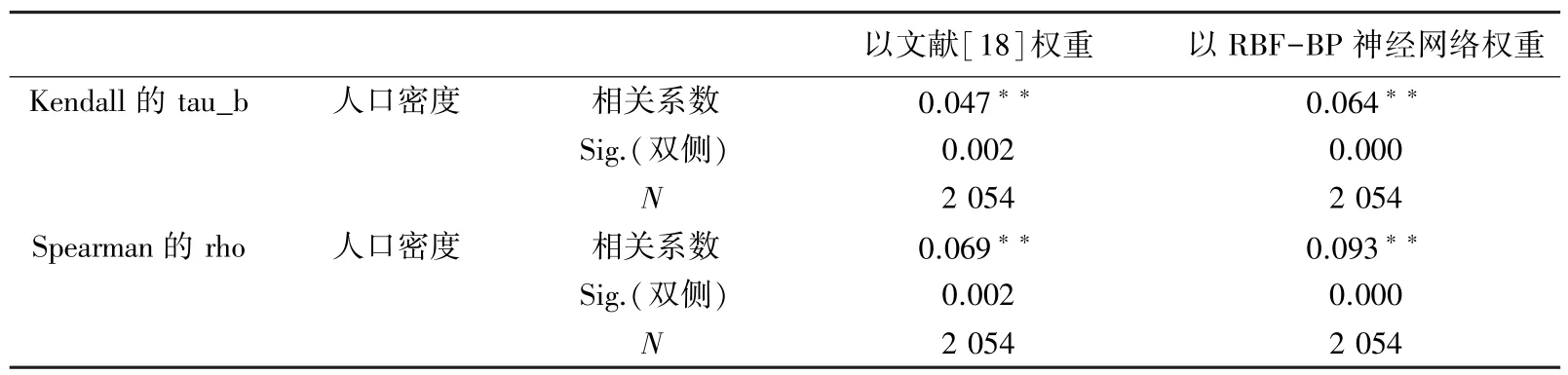
表6 Kendall的tau_b、Spearman的rho 相关系数比较Tab.6 Kendall＇s tau_b and Spearman＇s rho correlation coefficient comparison

4 结束语

RBF-BP 神经网络可将RBFNN的收敛速度快、稳定性好与BPNN 较强的反向自学能力、泛化能力强的优点融合在一起。首先，基于RBF-BP 神经网络算法建立的各因子相关性训练模型，反映了人居环境自然适宜性评价中，各个因子在综合评价结果中复杂的非线性关系，其能根据各指标对人居环境自然适宜性影响的大小，自动调节相关性权重，摒弃了人为赋予权重所产生的主观影响，具备良好的泛化能力；其次，RBF-BP 神经网络可以进行任意连续函数的非线性映射，更加准确地反映了各评价指标与评价结果之间的关系。结果表明，评价结果更客观、更科学地反应了区域人居环境的自然适宜性。