一道椭圆联赛题的解法
2022-02-28 02:27鲁媛媛
高中数学教与学 2022年1期
鲁媛媛
(江苏省仪征中学,211900)
竞赛试题是数学题目中的经典力作,大都蕴含丰富的数学思想方法,变化灵巧,精彩迭出.此外高考中的一些试题也带有竞赛题背景,特别是一些压轴题,往往是由竞赛题改编而来的.因此,重视对一些典型竞赛题的研究和探讨,实属必要.本文对2021年全国中学生数学奥林匹克竞赛(初赛)暨全国高中数学联赛中的第11题(压轴题)的解法进行探讨,希望能给您带来启发.
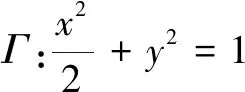
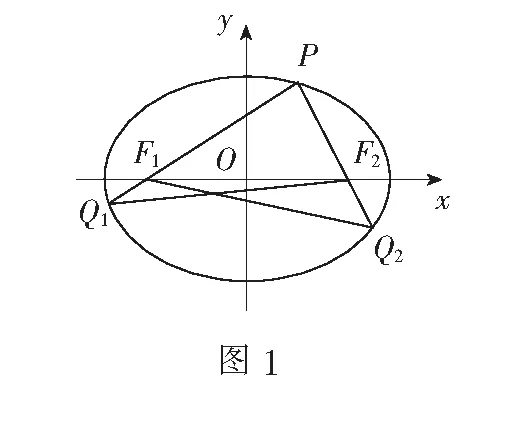
解法1易知焦点F1(-1,0),F2(1,0).设点P(x0,y0),Q1(x1,y1),Q2(x2,y2).由条件可知x0>0,y0>0,y1<0,y2<0.
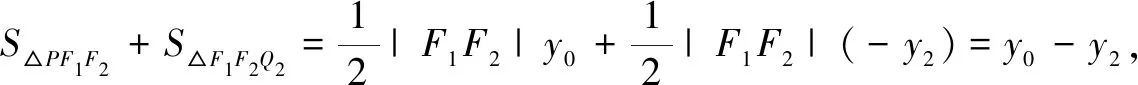
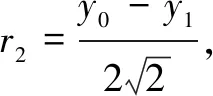
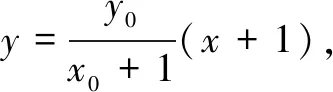
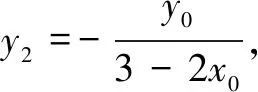
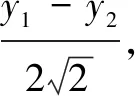
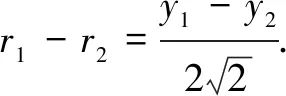
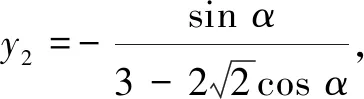
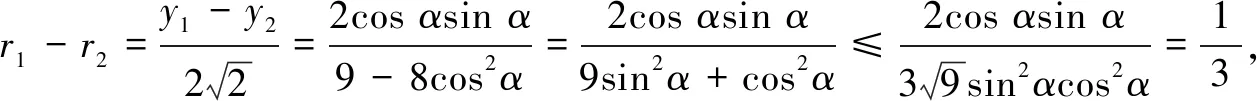
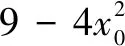
解法3同解法2,得
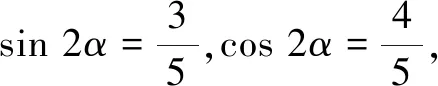
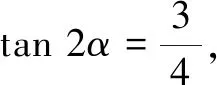
评注解法3在最后研究最值时没有象解法2那样运用基本不等式,而是结合辅助角公式和正弦函数的有界性求解的.其中式子3sin 2α+cos 2α的出现令人感到突兀,没有对知识左右逢源和信手拈来的功底及敏锐的洞察力是很难做到的.
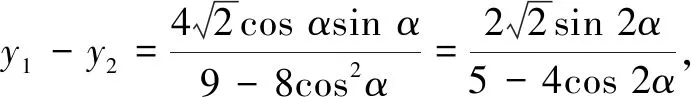
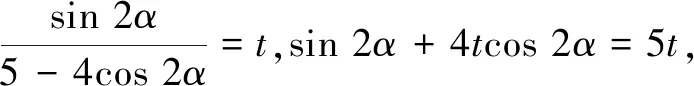
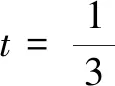
评注解法4在最后研究最值时也没有象解法2那样运用基本不等式,而是将r1-r2的表示式换元后结合辅助角公式及正弦函数的有界性转化为不等式求解.其中“取等”后结合三角公式求解相应的坐标是一道坎.
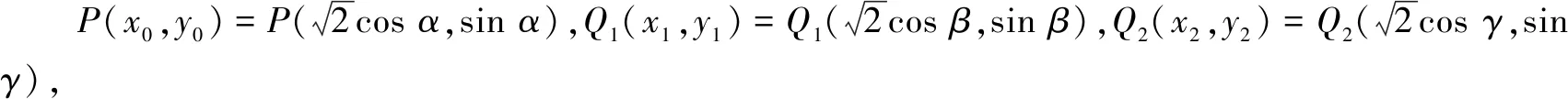
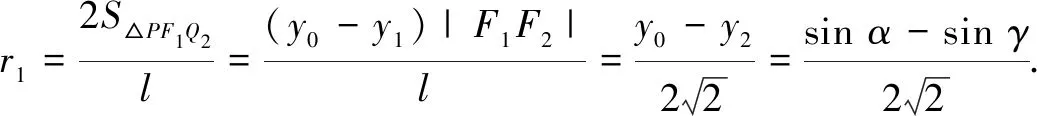
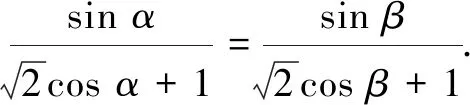
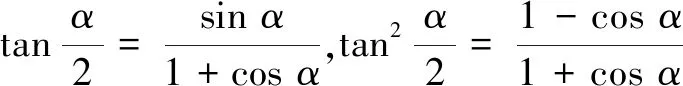
猜你喜欢
中等数学(2022年4期)2022-08-29
中学生数理化(高中版.高二数学)(2022年6期)2022-06-30
中学生数理化(高中版.高二数学)(2022年6期)2022-06-30
新高考·高三数学(2022年3期)2022-04-28
中学生数理化(高中版.高二数学)(2021年4期)2021-07-20
中等数学(2020年7期)2020-11-26
中等数学(2020年4期)2020-08-24
中学数学杂志(初中版)(2019年4期)2019-09-18
中等数学(2019年5期)2019-08-30
中学生数理化·高一版(2018年6期)2018-07-09

