唱大轴的导数

单 墫

(江苏省南京师范大学数学与计算机科学学院，210023)

近来,大轴题(最后一题)常常是导数的应用.如下面的这道题.

题目证明函数y=ex-1-2lnx+4x-6的图象不在函数y=(x-2)3的图象下方.

这道题就是要证明x>0时,恒有

f(x)=ex-1-2lnx+4x-6-(x-2)3

≥0.

①

证明一般分为两步:

(1)找一个值x=a,使① 式的左边为零,这个a就是f(x)取最小值时的点.通常可由观察法获得,而且f(a)是比较容易计算的.例如本题a=1,f(1)=e0-2ln 1+4-6+1=0.

(2)求f′(x),证明在00,从而f(x)单调增,f(x)≥f(1)=0.

理论很简单,但实际操作起来却会遇到困难.困难不在求导数,而在不等式的证明.教材中缺少不等式证明的内容,不加以补充,在这里便遭遇滑铁卢了.

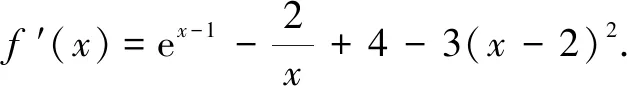
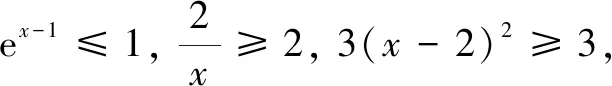
但在x≥1时,

②

不是很好证明.

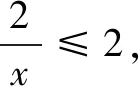
ex-1+2-3(x-2)2≥0 (x≥1).

③

第三,将能很快证明的部分先证明.我们要证明③ 式在x≥1时成立,一步证出有困难,可分为两步.

在[1,3]上,(x-2)2≤1,ex-1+2-3(x-2)2≥1+2-3=0,所以f′(x)≥0,f(x)单调增,有f(x)≥f(1)=0.

最后,再全力处理区间[3,+∞).可令t=x-2(使符号简单一些),则问题等价于证明t≥1时,

h(t)=et+1+2-3t2>0.

④

(t=1即x=3的情况,上面已经证明.当然现在直接验证也不难:e2+2>3)

要证明④ 式,依然用导数.h′(t)=et+1-6t,h″(t)=et+1-6,当t≥1时,h″(t)≥e2-6>2.72-6>2.52-6=0.25>0,所以h′(t)单调增.又h′(1)=e2-6>0,所以h′(t)≥h′(1)>0,得h(t)单调增,从而t≥1时,④ 式成立,即③ 式成立,从而② 式成立.证毕.