由一道质检题引发的圆锥曲线有关性质探究

顾旭东

(江苏省海门中学，226100)

众所周知,圆锥曲线题是高考压轴题的重点题型,因此,研究圆锥曲线的性质具有重要意义.本文以一道质检题为例,通过变形整合演绎出圆锥曲线的若干有趣结论,现抛砖引玉,与读者分享.

山东省济宁市2019届高三一模给出了如下质检题.

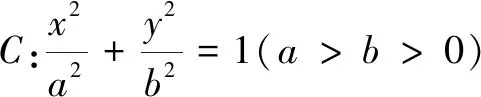
(1) 求椭圆C的方程;

(2) 设椭圆C的右焦点为F,直线l与椭圆相切于点A,与直线x=3相交于点B,求证:∠AFB的大小为定值.

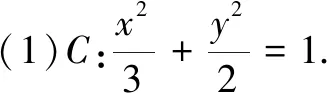
(2) 由(1)易知x=3为椭圆的右准线,由此联想问题的一般性,得解法如下.

由例1第(2)问的解答过程,可得

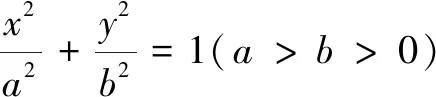
在以上探究中,若过点B作椭圆的另一条切线BD(D为切点),连结FD,同理BF⊥DF.这就顺理成章地得到如下的结论2.

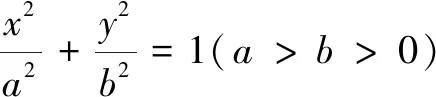
逆向探究,我们可得到如下的结论3.

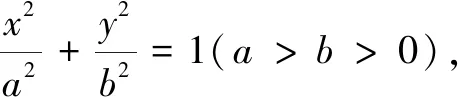
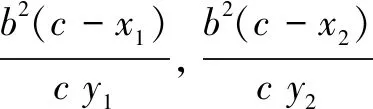
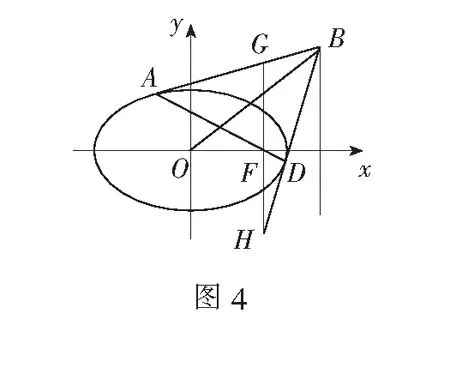
在图2中连结OB,经过观察及验证,发现OB平分AD,由此得到如下的结论4.

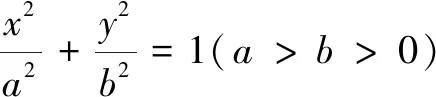
继续整合探究.过焦点F作x轴的垂线,交切线BA,BD于点G,H,直观猜测GF=FH,并通过论证得到如下的结论5、结论6.

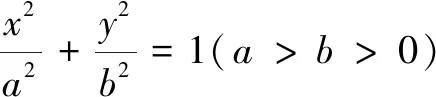
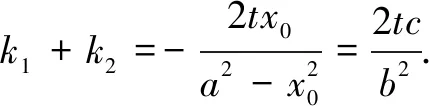
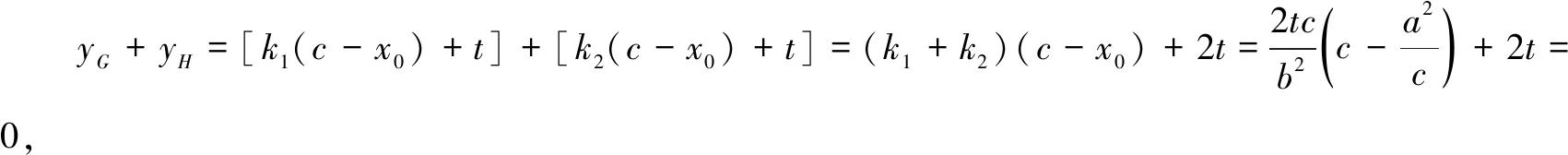
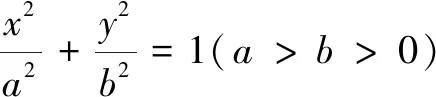
在图1中,若过原点O作AB的平行线交AF于点P,可得到如下美妙的结论.

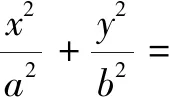
无独有偶,若在图6中再添加一条平行线,可得如下结论.

证明设直线AB的斜率为k,则直线A1B1的方程为y=kx.与椭圆方程联立,可得

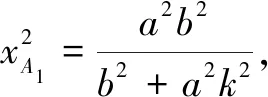
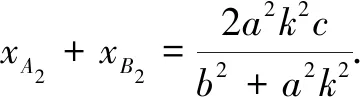
|A2B2|=2a-e(xA2+xB2)

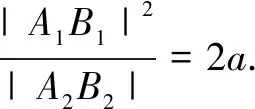
上述结论也可以类比到双曲线与抛物线,有兴趣的读者不妨进行探究,限于篇幅,在此不一一赘述.