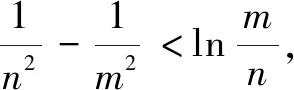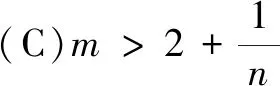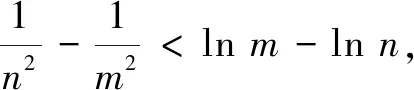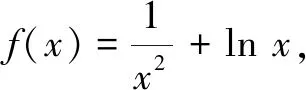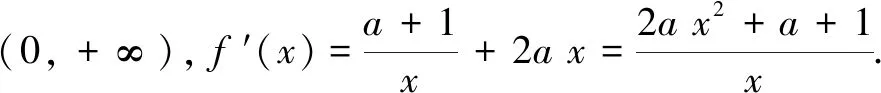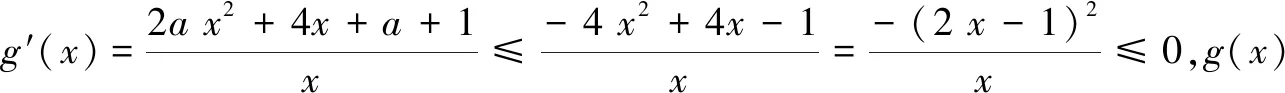巧构函数求解不等式问题

朱成万

(浙江省杭州市第十四中学,310006)

函数的单调性与不等式问题密切相关.用函数的单调性解不等式问题,首要任务是关注其代数式的结构.以单调增函数为例,其核心结构是:若α>β, 则f(α)>f(β);反之,若f(α)>f(β),则α>β.这个代数结构有两个显著特征:(1)条件与结论都是不等式;(2)不等式两边所含的字母或代数式的结构是一致的.

因此,遇到具有上述两个特征的不等式问题,就可以构造函数,并利用其单调性解题.本文试举几例,以飨读者.

例1(2020年全国高考题)若2x-2y<3-x-3-y成立,则( )

(A)ln(y-x+1)>0

(B)ln(y-x+1)<0

(C)ln|x-y|>0

(D)ln|x-y|<0

分析题设条件不等式的结构是以“底数”为标准归类,即将底数相同的放在一边,这样看不出x与y之间的关系.所以我们要调整不等式,以“幂”为标准归类,即将含x的式子放一边,含y的式子放另一边,得到2x-3-x<2y-3-y,由此构造函数f(x)=2x-3-x,利用其单调性求解.

解由条件得2x-3-x<2y-3-y.构造函数f(x)=2x-3-x,则f(x)

于是y-x+1>1,得ln(y-x+1)>0.故选A.

(A)m>n(B)m

评注例1和例2都是通过构造函数,利用函数的单调性解题.其关键是调整不等式,使不等式两边所含的字母或代数式的结构是一致的,即利用单调性代数结构的第二个特征解题.

例3(2012年浙江高考题)设a>0,b>0.则有( )

(A)若2a+2a=2b+3b,则a>b

(B)若2a+2a=2b+3b,则a

(C)若2a-2a=2b-3b,则a>b

(D)若2a-2a=2b-3b,则a

分析题设4个选项的结构特征是:条件是等式,结论是不等式,因此需将等式化为不等式,使条件与结论的代数结构一致.

解若2a+2a=2b+3b,必有2a+2a>2b+2b.构造函数f(x)=2x+2x,则f(a)>f(b),结合f(x)在(0,+∞)单调增,得a>b成立.故选A.

评注选项A正确,可排除B.其余选项用同样方法排除.

例4(2020年全国高考题)若2a+log2a=4b+2log4b,则( )

(A)a>2b(B)a<2b

(C)a>b2(D)a

解由条件,可得2a+log2a=22b+log2b<22b+log22b.

构造函数f(x)=2x+log2x,则f(a)

评注例3和例4也都是通过构造函数,利用函数的单调性解题.其关键是化等式为不等式,使条件与结论都是不等式,即利用单调性代数结构的第一个特征解题.

例5(2020年辽宁高考题改编)已知a≤-2,函数f(x)=(a+1)lnx+ax2+1.求证:对任意x1,x2∈(0,+∞),恒有|f(x1)-f(x2)|≥4|x1-x2|.

不妨设x1≥x2,则|f(x1)-f(x2)|≥4|x1-x2|等价于f(x2)-f(x1)≥4x1-4x2即f(x2)+4x2≥f(x1)+4x1.

综上,对任意x1，x2∈(0,+∞),恒有|f(x1)-f(x2)|≥4|x1-x2|.得证.

评注本题求解的关键是将不等式|f(x1)-f(x2)|≥4|x1-x2|去绝对值,将目标不等式转化为f(x2)+4x2≥f(x1)+4x1,从而构造函数g(x),并利用单调性求解.