由一道高考题谈一类问题的处理策略

韩宏帅

(山东省枣庄市台儿庄区教育局，277400)

题目(2021年全国高考题)已知点P在圆(x-5)2+(y-5)2=16上,点A(4,0)，B(0,2),则( )

(A) 点P到直线AB的距离小于10

(B) 点P到直线AB的距离大于2

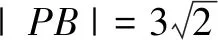
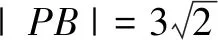
分析计算出圆心到直线AB的距离,得出点P到直线AB的距离的取值范围,可判断选项A,B的正误;分析可知,当∠PBA最大或最小时,PB与圆M相切,利用勾股定理可判断C,D选项的正误.

评注本题考查圆的方程及直线与圆的位置关系,考查直观想象、逻辑推理及数学抽象的核心素养.由于圆既能与平面几何相联系,又能与圆锥曲线相结合,命题方式比较灵活,故与圆相关的最值问题备受命题者的青睐.

圆的方程及直线与圆的位置关系一直是高考热点.通常作为客观题考查,其中长度、面积的计算,以及参数问题与最值问题是考查热点.常用的解题策略主要有:利用圆的几何性质、直线与圆的位置关系、平面图形的几何性质,运用数形结合的思想方法,有些与圆有关的最值问题还需要运用转化思想, 将问题转化为寻求与圆的半径相关的函数关系,借助函数求最值的方法进行求解，等等.这就需要我们熟悉圆的常见基本结论,在数形结合中寻找解决问题的突破口.

下面举例说明.

例1圆x2+y2+2x-8=0截直线y=kx+1(k∈R)所得的最短弦长为( )

解直线y=kx+1过定点A(0,1),圆的方程可化为(x+1)2+y2=32,故圆心为M(-1,0),半径r=3.

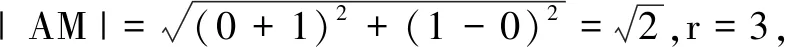
评注本解法的关键是挖掘直线过定点的隐含条件,判断定点与圆的位置关系,利用圆的垂径定理使问题获解.

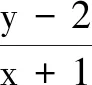
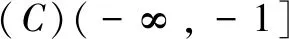
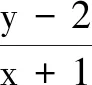
评注本解法的关键是利用目标函数的几何意义,在数形结合中借助直线与圆的位置关系使问题获解.

例3“曼哈顿距离”是由赫尔曼·闵可夫斯基所创的词汇,是一种使用在几何度量空间的几何学用语.例如在平面直角坐标系中,点P(x1,y1)，Q(x2,y2)的曼哈顿距离为LPQ=|x1-x2|+|y1-y2|.若点P(1,2),点Q为圆C:x2+y2=4上一动点,则LPQ的最大值为( )

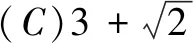
解设点Q(2cosθ,2sinθ)(0≤θ<2π),则LPQ=|1-2cosθ|+|2-2sinθ|.

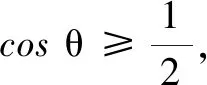
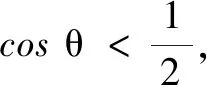
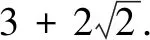
评注本解法的关键是在读懂“曼哈顿距离”概念的基础上列出目标函数表达式,再运用数形结合、分类讨论的手段去掉绝对值符号,结合三角函数知识求解.

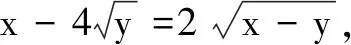
(A)4 (B)18 (C)20 (D)24

解由条件知y≥0,x≥y≥0.

当x=0时,解得y=0,符合题意.

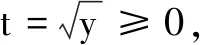
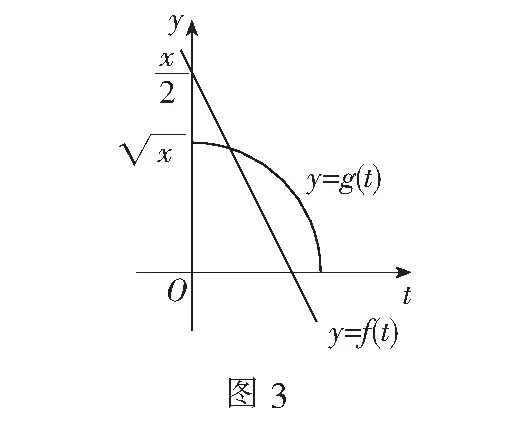
如图3,观察可知当直线与圆相切时,由

综上,x∈[4,20]∪{0},x的最大值为20.故选C.

评注本题需要在弄清变量取值范围的基础上灵活变更问题的表达方式,将方程有解问题转化为函数图象有交点问题,化陌生为熟悉.