基于端对端通信的充电桩无功响应分布式模型预测控制策略

胡金迪，刘 思，沈 广，叶承晋，丁 一，鲍卫东

（1. 浙江大学电气工程学院，浙江省杭州市 310027；2. 国网浙江省电力有限公司营销服务中心，浙江省杭州市 310000；3. 浙江电力交易中心有限公司，浙江省杭州市 310007；4. 国网义乌市供电有限公司，浙江省义乌市 322000）

0 引言

在推进新型基础设施建设背景下［1］，新能源汽车充电桩具有广阔前景，其规模将持续快速增长。但在部分地区，充电桩面临综合利用率较低的现实问题，2018 年全国公共充电设施的平均小时利用率不足10%［2］，如何提升充电桩利用率已经成为热点问题。部分研究关注其优化选址，在规划阶段尽可能衔接城市发展，提升交通流量捕获能力。文献［3］对车辆空间行为特性进行分析并以此建立充电站选址模型。文献［4］综合考虑车流信息与电网约束实现充电站规划方案优选。而关于存量充电桩闲置率提升的研究则多从运行层面开展。

由于间歇性分布式新能源渗透、地铁等大功率冲击性负荷接入、电缆化率提升造成容性无功过剩以及线路故障等原因，配电网存在大量无功瞬时平衡需求［5］。利用充电桩变换器的无功双向运行特性实现无功补偿，是解决存量充电桩闲置问题的途径之一。文献［6-7］通过理论推导与实际测量验证了三相充电桩具有无功响应的潜力。在电动汽车蓄电池或稳压电容的支撑下，充电桩通过调整功率开关的通断，使变换器输出设定电压波形，从而实现有功、无功传输［8］。而且充电桩的无功响应过程不会影响电动汽车的充电活动，也不会缩短电池寿命［7-8］。文献［9］提出了电动汽车智能充放储一体化电站的无功电压调控策略，实现了无功就地补偿。文献［10］建立了电网-运营商分层调度模型，通过充电站间的协调响应，提供无功补偿，减小电压偏差。相比于公共充电站，居民充电桩数量更为庞大，分布广泛且稀疏。目前，居民充电桩的无功响应策略研究多聚焦在统一调度、集中控制方面［11］，但随着居民充电桩保有量快速增加，其集中控制面临严重的维数灾问题，且中低压电网的二次通信基础设施相比于高压电网明显薄弱，传统单中心的控制模式难以完全实现用户侧海量设备的高效控制。因此，分布式策略逐渐成为充电桩等用户侧设备控制的热点方向［12］。

在分布式控制模式下，通信延迟将导致单元间无法实时共享数据，进而限制调控效果。而模型预测控制（model predictive control，MPC）可预测未来一段时间内被控对象的状态，通过交互预测信息可降低通信延迟的影响。MPC 是目前电力电子控制领域应用广泛的控制算法，主要由预测模型、滚动优化、反馈校正3 个部分组成［13］，具有响应速度快、控制精度高的优点［14］。文献［15-16］基于MPC 建立了协调风机与静止无功发生器（SVG）的风电场电压控制方法，在并网点实现无功补偿。文献［17］建立了分布式模型预测控制（distributed model predictive control，DMPC）策略，实现储能设备参与电压调控。文献［18］通过DMPC 调整微网内功率单元的有功和无功功率，实现微网调压调频。但在考虑充电桩运行特性的DMPC 调压策略方面，还缺少深入研究。

为提升充电桩的容量利用率，挖掘其无功响应潜力，本文提出了基于端对端通信的充电桩无功响应DMPC 策略。首先，建立有功功率以及容量约束下的充电桩无功响应模型，将多桩集群无功响应的复杂集中式优化问题解耦为各桩分布式协同子问题；然后，通过基于时间戳异步更替的端对端通信策略交互邻域充电桩预测信息，并采用滚动优化与反馈校正策略减少调压偏差，提升整体调压效果。

1 基于端对端通信的充电桩无功响应DMPC 框架

为汇聚各充电桩的闲置无功资源，实现配电网电压偏差协同优化，本文建立基于端对端通信的充电桩无功响应DMPC 策略。其框架主要由控制算法与通信策略两部分组成。其特点在于将涉及充电桩集群多点控制变量的优化问题解耦为若干子问题，每个充电桩仅需求解自身的控制变量，并建立基于时间戳异步更替的通信策略，通过邻域端对端通信交互实现所有充电桩间的最优协同无功响应。单个充电桩的整体无功响应框架如图1 所示。

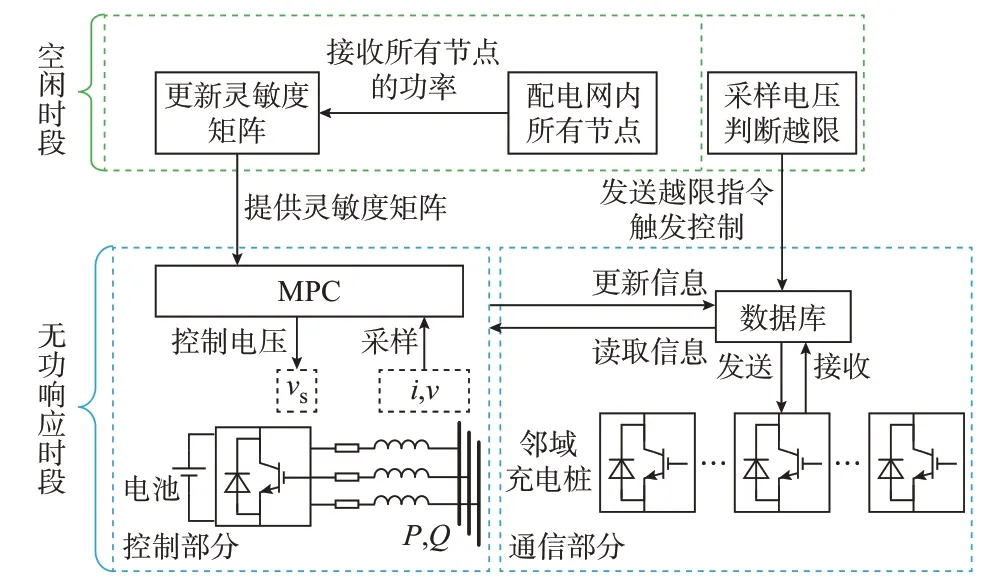
图1 单个充电桩的无功响应框架Fig.1 Framework of reactive power response for a single charging pile

在空闲时段，每个充电桩将定时获取配电网内所有节点的功率信息，并根据预存的线路参数，计算与更新灵敏度矩阵，其更新速率由配电网功率更新的频率决定。同时，检测充电桩所处节点的电压，若超过阈值，则发送指令，通知所有充电桩开始无功响应。

在无功响应时段，首先，采样节点电压v和线路电流i，并从数据库读取其他充电桩的有功功率、无功功率、电压信息。然后，建立充电桩电流和电压的预测模型，进行DMPC 计算，确定充电桩变换器的输出电压vs，同时采用滚动优化、反馈校正机制减小误差。最后，通过基于时间戳异步更替的邻域端对端通信策略，实时接收信息并更新数据库，同时向邻域充电桩发送信息，最终实现所有充电桩的整体最优协同响应。在整体电压偏差恢复正常后，各充电桩退出无功响应，重新进入空闲时段。

实现上述无功响应功能要求充电桩满足一定配置条件，包括计量、通信与边缘计算功能，这些装置仅涉及二次系统，无须对电力电子交直流变换器本体进行改造。且本文所提的控制策略对通信延迟不敏感，配备公网通信设备即可，无须额外铺设专用通信线路。相比于静止无功补偿器（SVC）、SVG 等较为昂贵的调节治理装置，充电桩二次改造投资相对较小。而且，除无功补偿外，充电桩还可以参与电力系统调峰、调频等辅助服务。相比于仅用于无功补偿的电容器、SVC、SVG 等装置，充电桩改造的盈利模式更为多元。在调节特性上，投切电容器只能进行有级调节；SVC 装置虽能连续输出无功功率，但仅限于容性或感性无功功率，无法双向输出；SVG装置的成本最高。以上常规电压治理装置普遍布置于线路首端，对分布式电源渗透、电压波动频繁的馈线末端补偿作用有限。因此，本文所提的充电桩调压策略具备经济性，且在调压效果上相比传统方式更接近用户，具有平滑、双向等优势。

2 充电桩DMPC 算法

本章提出的DMPC 算法将所有可控变量的求解分配到对应的充电桩，每个充电桩只需计算两个控制变量，与集中式控制相比计算成本更低。该控制算法首先通过通信获取其他充电桩的功率以及电压信息，并通过计量单元采样所在节点的电流和电压。然后，构建充电桩无功响应的目标函数，基于瞬时功率理论与灵敏度矩阵建立状态方程与功率约束条件。最后，通过滚动优化与反馈校正减小控制偏差，实现充电桩集群无功响应。

2.1 充电桩无功响应预测模型的建立

本文所有充电桩均采用相同优化控制模型和逻辑，以充电桩m为例进行阐述。

2.1.1 充电桩无功响应目标函数

充电桩的无功响应目标为降低配电网内所有充电桩节点的整体电压偏差，即在设定的预测周期内，各充电桩所在节点的电压偏差平方和Jm(k)最小，对应的目标函数如式（1）所示。

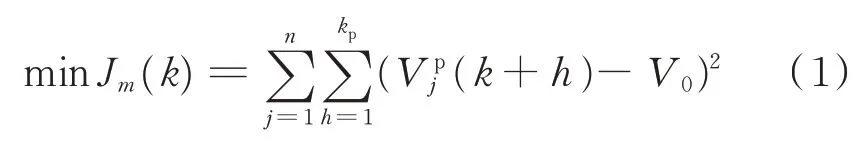
式中:k为当前周期；n为参与调压的充电桩数量，若存在接入多个充电桩的节点，则将其拆分为多个节点，使得每个节点最多只连接一个充电桩，因此，n同时也为参与调压的节点数量；kp为预测周期数；Vpj(k+h)为充电桩j所在节点的电压在未来k+h周期初始时刻的预测值；V0为电压目标值，本文中设定为1 p.u.。

目前，配电网中的普通负荷实时采样电压的速率尚未达到秒级，若考虑优化所有节点的电压偏差，将显著增大计量成本与通信负担。因此，式（1）仅考虑充电桩所在节点的电压偏差。此外，由于居民充电桩分布广泛，本文采用的目标函数也能近似代表配电网的整体电压偏差。

2.1.2 充电桩电流电压状态方程

本文基于瞬时功率理论［19］对图1 中的节点电压v、流入充电桩的线路电流i、变换器网侧输出电压vs分别通过Park 变换提取对应的dq分量作为状态变量或控制变量，其中参考相位取节点电压v的相位。通过对应变量的dq分量与线路参数来构建充电桩电压、电流的状态方程。

本文预测模型的周期为秒级，远小于配电网节点每5 min 或每15 min 的功率更新间隔。因此，在预测模型中可认为其他节点的功率为定值，式（6）与式（7）中的灵敏度矩阵仅考虑充电桩的功率变化，未考虑其他节点。但灵敏度矩阵需要配电网中各节点的功率信息支撑，且难以实时计算。因此，灵敏度矩阵的计算将在无功响应尚未开始的空闲时间内进行。各充电桩将预存线路的参数信息，然后依据节点功率的更新时间，每5 min 或15 min 通信获取所有节点的功率信息，最后计算并更新预测模型中的灵敏度矩阵。

2.1.3 充电桩无功响应约束条件

充电桩无功响应的约束条件主要为功率约束。充放电过程中，充电桩均具备无功补偿能力，其无功补偿范围如附录A 图A1 所示［22］。

本文提出的控制策略不会干扰充电桩的有功交互过程，仅利用当前有功功率下剩余的无功潜力实现无功响应，即在无功响应的同时，电动汽车的充放电活动仍可正常进行，并将其充放电需求范围作为无功响应的约束条件，由此可得其功率约束如式（10）—式（12）所示。

由式（10）可计算得到充电桩有功、无功功率的预测值。式（11）为充电功率约束，该约束确保无功响应时充电桩的有功交互不会被影响。式（12）为容量约束，保证充电桩在额定容量内运行。

此外，无功响应过程还需考虑电压幅值约束，如式（13）—式（15）所示。

式（13）为充电桩的节点电压幅值约束，保证无功响应过程中节点电压在合理范围内，避免超调振荡。式（14）和式（15）为充电桩变换器控制电压d、q轴分量的幅值约束，防止损坏变换器。

2.2 DMPC 流程

首先，设定无功响应的触发阈值和结束阈值，当充电桩的节点电压存在越限时，该充电桩将通知其他充电桩开始进行无功响应。然后，各充电桩通过DMPC 实现协同优化。最后，当电压偏差低于结束阈值时，无功响应结束，各充电桩定时更新灵敏度矩阵，并检测电压是否越限。

无功响应期间，充电桩以采样得到的电压、电流以及通信接收的其他充电桩电压为状态变量初始值，以其他充电桩功率变化量通信值为参数，在线求解各自优化模型。求解过程中，控制周期为kc，预测周期为kp，其具体含义为:各充电桩以未来kp周期内的电压偏差最小为目标求解优化模型，确定未来kc周期内的控制变量设定值，而随后kp-kc周期内控制变量保持上一周期的值不变。

完成模型求解后，DMPC 采用滚动优化、反馈校正减小控制偏差，其时域控制逻辑如附录B 图B1所示。

2.2.1 滚动优化

若直接将求解结果作为未来kc周期内控制变量的设定值，则在下一次求解前，控制偏差将随着周期的推移而累积增大。因此，完成优化模型求解后，计算结果将仅作用于当前周期，而预测信息将发送到邻域充电桩。各充电桩将在每个周期的初始时刻重新采样并求解模型，更新控制变量的设定值，实现滚动优化。

2.2.2 反馈校正

由于系统建模难以完全精确、端对端通信下各节点实时信息不同步以及数据采样误差等因素，预测结果与实际之间存在偏差成为MPC 的共性问题［23］。因此，本文对预测模型结果进行反馈校正，形成闭环控制，减小预测偏差。具体地，充电桩完成采样后，根据状态变量采样值与预测值的偏差，校正预测模型中的对应参数。

参与反馈校正的变量包括线路电流的dq轴分量、节点电压及其相角，其校正逻辑与附录B 图B1中节点电压的反馈校正相同。式（4）—式（7）中的id，offset(k)、iq，offset(k)、θoffset(k)、Vm，offset(k)为 充 电 桩m的偏差校正量，其计算公式如下。

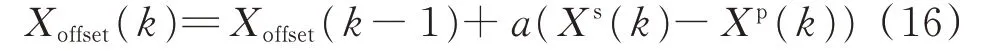
式中:X表示电流i的d、q轴分量id、iq、相角θ、节点电压幅值Vm；a为偏差系数；上标s 和p 分别表示对应变量的采样值和预测值。

3 基于时间戳异步更替的邻域端对端通信策略

DMPC 将计算预测周期内有功、无功功率以及电压的预测值，同时生成时间戳，以记录信息的产生时间。时间戳与预测值通过邻域端对端通信传递至所有充电桩并更替旧时间戳的信息，总体通信策略如附录C 图C1 所示。相比于集中式控制策略，采用仅需邻域充电桩之间异步通信的分布式控制策略对通信的实时性要求更低，可减少通信开销。端对端通信的具体交互过程分为通信内容、通信流程、更新策略3 个部分。

3.1 通信内容

各充电桩都建立了数据库存储其DMPC 预测结果与其余充电桩的信息。通信时，充电桩发送的内容与自己数据库中的内容完全一致。

数据库共存储n组预测数据及n个时间戳。每组数据为对应充电桩的功率、电压预测结果，并附有时间戳，以记录原始数据的生成时间。充电桩m关于充电桩j的存储信息包括:充电桩j的时间戳kj；有功增量ΔPcj(kj)，ΔPcj(kj+1)，…，ΔPcj(kj+kp-1)；无功增量ΔQcj(kj)，ΔQcj(kj+1)，…，ΔQcj(kj+kp-1)；电 压 预 测 值Vcj(kj)，Vcj(kj+1)，…，Vcj(kj+kp-1)。

特别地，在通信尚未开始的起始时期，暂缺的时间戳、有功增量、无功增量用0 替代，电压预测值用1 p.u.替代。

3.2 通信流程

对单个充电桩而言，通信流程如图2 所示。首先，根据充电桩的分布设定各充电桩的临近充电桩，并保证所有充电桩之间均能直接通信或通过中间充电桩间接通信。无功响应触发后开始通信，在通信过程中，对比接收前后的信息，若数据库被更新则将信息发送给临近充电桩，否则重新等待接收信息。最后，当整体电压偏差小于结束阈值时，结束通信与无功响应。

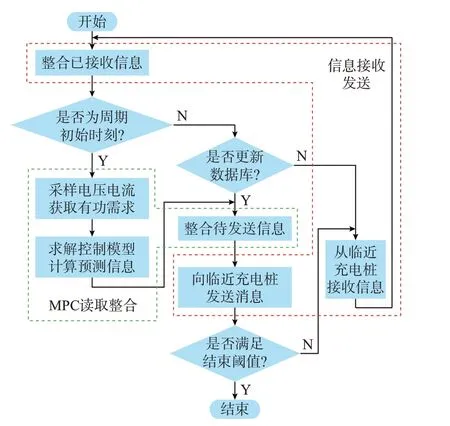
图2 通信流程图Fig.2 Flow chart of communication

同时，在每周期初始时刻求解DMPC。若数据库中的数据不能全部覆盖DMPC 的计算需求，则有功、无功增量缺少的部分用0 代替，电压值缺少的部分则用数据库中最近时间的电压值替代。DMPC计算完成后，有功、无功增量以及电压的预测结果将被更新至数据库。

3.3 通信内容更新策略

如附录C 图C1 所示，充电桩接收到来自邻域桩的通信内容，包括各充电桩的时间戳以及对应的有功、无功增量、电压预测值。充电桩接收这些信息后，根据时间戳进行整合，使数据库中的数据为最新。此外，在完成DMPC 计算后，充电桩将更新数据库中自己的时间戳、电压预测值以及有功、无功增量，其中电压预测值由式（7）计算相应的电压得到，有功、无功增量由式（9）得到。

4 算例分析

4.1 算例场景描述

为验证本文提出的控制策略的有效性，本节基于文献［24］的低压配电台区模型与文献［7，25］的充电桩模型建立仿真算例，模拟分布式光伏出力波动下台区电压越限及其恢复过程。该低压配电台区拓扑如附录D 图D1 所示。

由于天气原因，该区域光伏出力由最大功率的80%突然跌落至50%，在不平衡功率冲击下台区电压出现偏移。光伏出力正常时电压分布如图3 灰色曲线所示，光伏跌落时电压如图3 红色曲线所示。

图3 节点电压分布图Fig.3 Distribution diagram of node voltage

针对低电压问题，基于DMPC 进行充电桩无功响应控制。充电桩之间均双向通信，通信延迟为50 ms，邻近充电桩之间的通信拓扑可根据空间距离选定，本算例选取如附录D 图D1 所示的通信关系进行仿真。DMPC 算法模型中，周期设置为1 s，控制周期数、预测周期数均为3。各桩线路参数中，等效电阻为0.01 Ω，等效电感为120 mH。反馈校正的偏差系数均设定为0.5。

为对比充电桩响应与传统配电网调压方式的效果，在算例中设置了通过投切配电变压器侧400 kvar 电容器组进行无功补偿的场景。此外，根据文献［26］设定SVC 最佳补偿点为节点7 与节点11，如附录D 图D1 所示，其容量均设定为30 kvar。

4.2 充电桩电压支撑效果分析

电容投切后电压分布如图3 蓝色曲线所示，SVC 调压结果如图3 黄色曲线所示，充电桩参与调压后的电压分布如图3 绿色曲线所示。从图3 可以看出，光伏出力正常时，各节点电压均在0.95 p.u.以上，电压分布正常。光伏出力突然降低后，大部分节点电压出现严重偏移，其中节点6、7、10、11、18、19、20 的电压低于0.95 p.u.，此时各充电桩采用本文提出的分布式控制策略参与无功响应后，电压得到明显改善，所有节点电压均恢复到0.95 p.u.以上。投切电容可以提高线路末端电压，但是首端注入容性无功功率导致节点2、12、13、14、15 的电压过高，电网整体电压调节效果劣于充电桩在线路末端无功支撑的模式。算例优化结果下，位于节点7 与节点11的SVC 分别投入了29.8 kvar 与28.5 kvar 的无功功率来降低所在馈线的电压偏差，但无法有效调节其余馈线的电压，其调压效果劣于分布在各馈线进行无功补偿的充电桩。

为进一步分析不同无功补偿策略对电压分布的改善效果，定义电压偏差综合指标σV(t)如下。

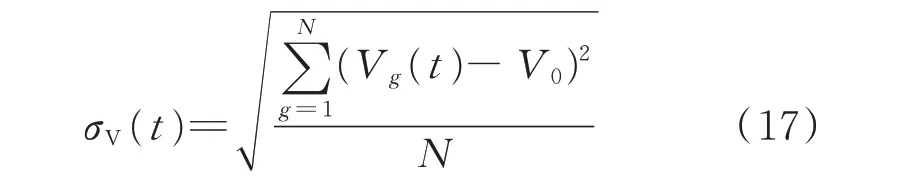
式中:N为节点总数；Vg(t)为节点g在t时刻的电压；V0为电压目标值，本文设为1 p.u.。

光伏正常出力、光伏跌落、充电桩参与调压时的电 压 偏 差 分 别 为 0.034 70 p.u.、0.056 47 p.u.、0.035 68 p.u.。可见，充电桩参与调压后，电压偏差接近光伏正常出力情形，相比于光伏跌落时，电压偏差降低了36.81%。此外，线路首端投切电容场景下的电压偏差为0.046 46 p.u.，SVC 调压场景下的电压偏差为0.038 05 p.u.，相比于这两个场景，充电桩调压的电压偏差分别降低了23.20%和6.23%。因此，本文提出的充电桩控制策略能有效提供无功补偿，达到末端电压支撑效果。

为验证目标函数仅考虑充电桩所在节点的电压偏差的可行性，算例还在本文控制策略的基础上设置了全局最优的场景。全局最优场景的目标函数为配电网台区内所有节点的电压偏差平方和最小，同时各节点实时采样电压并发送至所有充电桩。该场景下的电压偏差为0.034 44 p.u.，相比于采用本文控制策略时的电压偏差仅降低了3.49%。可见，本算例中仅考虑充电桩节点电压偏差的目标函数能近似替代考虑所有节点的全局最优目标函数，同时避免了全局最优控制下的采样成本与通信压力。

4.3 调压成本分析

根据文献［27］，投切电容的补偿成本包括运行成本与建设成本两部分。其中，总容量为5 Mvar 的投切电容组的建设成本为22 000 美元，投切电容的预防维护成本为每年3 600 美元，投切电容所在变电站进行调压操作的运行维护成本为每年6 000 美元，该投切电容组的使用寿命为10 年。按照美国加利福尼亚州35%的税率、3%的通胀率以及6%的资本成本进行计算，得到容量为5 Mvar 的投切电容的年均成本净现值约为14 000 美元，由此可得10 年使用周期下投切电容的补偿成本为28 美元/kvar，即178.6 元/kvar。

根据文献［28-29］，SVC 单位容量无功补偿成本与运行范围近似呈二次关系，其量化关系如式（18）所示，可得容量为30 kvar 的SVC 的无功补偿成本为812.5 元/kvar。文献［29］采用式（18）测算成本时，设定其寿命为5 年，则10 年无功补偿周期下，SVC 的 无 功 补 偿 成 本 为1 625 元/kvar。

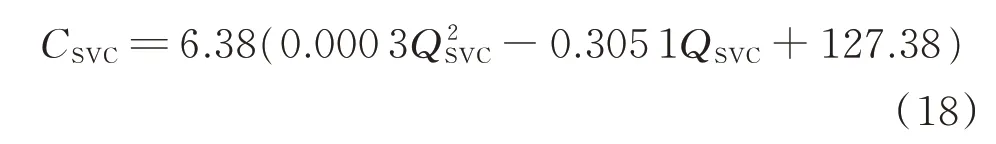
式中:CSVC为SVC 的单位容量无功补偿成本；QSVC为SVC 的容量［28］。

根据文献［30］可知，充电桩参与无功补偿的成本包括:功率控制模块改造成本、通信改造成本与运行成本。对于无功补偿范围为6.6 kVA 的充电桩而言，功率控制模块改造成本为49 美元，无功补偿通信改造成本为50 美元。运行成本为因无功补偿造成的额外功率损耗，满载时的功率损耗约为300 W，其运行成本计算方法为:文献［30］根据0.1 美元/(kW·h)的电价计费，每天有14 h 参与无功补偿，用于无功补偿的平均容量为额定容量的25%，在此工作条件下的使用寿命为10 年以及3%的通胀率，计算得到运行成本为452 美元。因此，10 年无功补偿周期下，充电桩参与无功补偿的总成本为551 美元，单位容量无功补偿成本为84 美元/kvar，即535.9 元/kvar。

根据以上参数，不同无功补偿策略的调压成本如表1 所示。

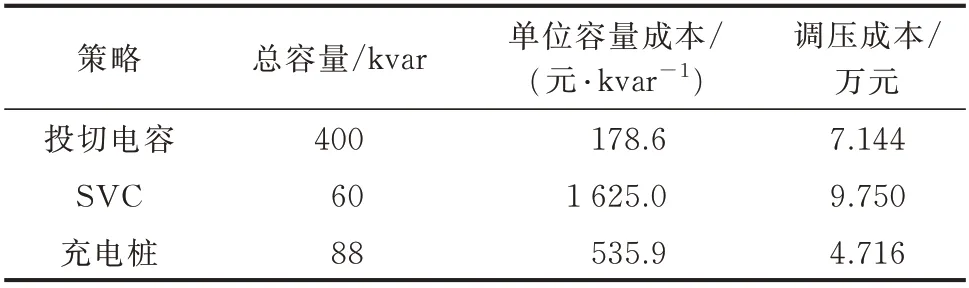
表1 不同无功补偿策略的调压成本Table 1 Voltage regulation cost of different reactive power compensation strategies

投切电容的调压成本高于充电桩，而且只能有级投切，无法连续补偿。SVC 的调压效果与充电桩接近，但其调压成本为充电桩的2.07 倍。因此，在综合考虑调压成本与调压效果后，充电桩调压相比于投切电容与SVC 更具优势。

4.4 充电桩功率分析

选取节点5 的充电桩分析功率情况，其功率曲线如图4 所示。充电桩在1 s 时开始无功响应，响应期间，充电桩的有功功率在6.22～7.43 kW 波动，仿真时间内有功功率平均值为7.15 kW，与设定充电功率7 kW 仅相差2.14%。

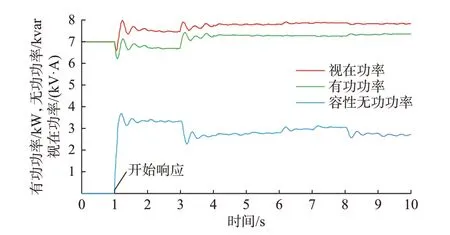
图4 节点5 充电桩功率Fig.4 Power of charging pile at node 5

可以看出在本文模型下，充电桩无功响应过程中可满足车辆的充电需求。此外，在无功响应期间，充电桩的视在功率峰值为7.98 kV·A，平均值为7.67 kV·A，充电桩在调控期间不会破坏容量限制。若充电桩未参与无功响应，其视在功率与有功功率相同，如图4 绿色曲线所示，视在功率平均值为7.15 kV·A。充电桩参与无功响应后，其视在功率如图4 红色曲线所示，平均值升高至7.67 kV·A，提升了7.27%。

为量化评估各充电桩容量利用的提升效果，定义容量利用率为已经利用的容量占额定容量的百分比，如式（19）所示。在本算例场景下，充电桩参与无功补偿时，各充电桩的功率与容量利用情况如表2所示。

表2 充电桩功率与容量利用率Table 2 Power and capacity utilization rates of charging pile

式中:Uall为区域内所有充电桩的容量平均利用率；Uj为充电桩j的容量利用率；Pj、Qj、Smaxj分别为充电桩j的有功功率、无功功率、额定容量。

在不参与无功响应的情况下，充电桩容量平均利用率为16.43%。若利用闲置充电桩以及正在有功交互的充电桩的可用容量进行无功补偿，则充电桩容量平均利用率可达95.16%，且各充电桩的容量利用率均高于80%。由此可见，本文所提的无功补偿策略能显著提升充电桩的容量利用率。

4.5 调压效果对通信延迟的敏感性分析

为分析本文提出的控制、通信策略在不同通信延迟下的调压效果，在算例中设置不同延迟进行仿真。在开始响应时，即图5 中1～2 s 期间，不同通信延迟下的电压曲线均一致。这是由于响应的初始时刻充电桩之间尚未通信，优化模型求解结果相同。此后，充电桩开始相互通信，不同延迟下的电压曲线出现差异。从图5 可以看出，相比于无通信的充电桩无序响应模式，充电桩之间保持通信时电压偏差更小，但通信时延对调压效果有负面影响。

图5 不同场景下电压偏差综合指标曲线Fig.5 Comprehensive indicator curves of voltage deviation in different scenarios

为进一步比较不同时延下的调压效果，定义全过程电压偏差指标σall如式（20）所示。不同通信延迟下的调压指标对比如表3 所示。

表3 不同通信延迟下的调压指标对比Table 3 Comparison of voltage regulation indicators with different communication delays

式中:T为各节点电压在仿真时的采样时间点数。

从图5 和表3 可以看出，无通信控制模式下的偏差较大，其全过程偏差大于0.04 p.u.；而端对端通信策略下，控制效果得到了明显改善，延迟在1 s 之内的全过程偏差均低于0.04 p.u.。随着通信延迟的不断降低，其全过程电压偏差指标相比于无通信控制分别降低了6.68%、7.56%、10.19%、11.45%。同时，表3 给出了在2～10 s 期间电压偏差指标σV(t)的峰值，随着时延不断降低，偏差峰值相比于无通信控制分别降低6.48%、7.29%、8.88%、9.64%。定义达到稳定值±5%的时间为调节时间，表3 给出了不同通信延迟场景下的调节时间。相比于无通信控制，端对端通信模式的调节时间分别缩短了36.91%、36.44%、47.95%、48.11%。

仿真结果表明，本文提出的分布式控制策略在不同延迟下均有良好效果，对通信延迟的鲁棒性较强，且相比于无通信控制策略具有明显优势。

4.6 分布式策略与集中式策略控制效果分析

根据本文的目标函数、预测模型与约束条件，建立集中式控制模型。各充电桩将电流、电压采样值发送至控制中心，然后由控制中心计算各充电桩的控制电压设定值，并发送至各充电桩。图5 给出了集中式控制在200 ms 通信延迟下的电压偏差综合指标曲线。另外，通过i5-4590T 2.00 GHz CPU 计算机在MATLAB R2020a 中求解MPC，比较分布式控制与集中式控制的计算时间，如表4 所示。

表4 分布式控制策略与集中式控制策略对比Table 4 Comparison of distributed control strategy and centralized control strategy

从图5 可以看出，相比于分布式控制，集中式控制每次响应都延迟了400 ms。由表4 可知，集中式控制需要的计算时间显著增加，占据了更多的计算资源，且全过程电压偏差指标增大了4.47%。可见，所提分布式控制策略能减轻计算负担，其控制效果与集中式控制相似，能有效实现充电桩间的协同响应。

此外，集中式控制的控制信息由控制中心统一发送，一旦控制中心出现计算错误或受到攻击，则无法实现无功响应。所提的分布式控制策略采用对等架构，即使部分设备受到攻击，其余充电桩仍可进行无功响应，相比于集中式控制具有优势。

5 结语

本文提出了一种基于端对端通信的充电桩无功响应DMPC 策略，利用充电桩在有功水平下的剩余无功容量调节低压配电网的电压。其中，DMPC 算法基于瞬时功率理论与灵敏度矩阵构造充电桩无功响应的状态方程、约束条件，通过预测模型、滚动优化、反馈校正求解变换器控制电压设定值。然后，建立基于时间戳异步更替的通信框架，通过邻域充电桩端对端通信，将优化问题解耦，并实现逼近全局最优的协同响应，算例仿真结果表明:

1）提出的分布式控制策略能有效利用充电桩的无功响应容量，从而应对新能源出力意外跌落导致的电压越限问题，改善低压配电网的电压质量，相比于投切电容、SVC 的传统方法调压效果更好；

2）所提控制策略在无功响应过程中不会影响有功充电需求，可提升充电桩的容量利用率；

3）所涉及的基于时间戳异步更替的邻域端对端通信策略具有较好的通信延迟鲁棒性，相比于不进行通信的无序控制，调压效果更佳。

所提控制策略对通信延迟要求较低，无须建设专用通信线路，二次设备改造成本相对较小，具有经济性。此外，所提策略可被进一步推广应用于储能、光伏等带有电力电子变换设备的用户侧资源，调用其参与配电网无功调节，应用场景广泛。

本文受到国网浙江省电力公司科技项目(5211YF20000R)资助，特此感谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。