“工”字型径向弹性超材料零频起始带隙特性研究

李丽霞， 贾 琪， 解妙霞， 李 玲， 张锡成

(1. 西安建筑科技大学 机电工程学院 机械动力所，西安 710055；2. 西安建筑科技大学 力学研究院，西安 710055；3.西安建筑科技大学 土木工程学院 工程结构与抗震研究所，西安 710055)

声子晶体[1-2]是一种可以控制固体中弹性波的周期性结构，因其带隙特性受到研究人员的广泛关注，现有的带隙形成机制主要为布拉格散射机制[3-5]与局域共振机制[6]。其中，基于布拉格散射机制的声子晶体，带隙产生的主要原因是周期变化的材料特性与弹性波的相互耦合作用,散射体的尺度和带隙频率所对应的波长位于同一数量级，因此需要大的空间尺寸才能阻隔振动。基于局域共振机制的声子晶体[7]，在弹性波激励下，散射体振子产生共振，并且与弹性波相互作用，进而带隙频率远低于相同晶格尺寸的布拉格带隙，实现了小尺寸控制大波长，以局域共振机制为主的声子晶体也称为弹性超材料[8-11]。

为了促进弹性超材料在振动控制和机械工程中的应用，获得低频及大带宽带隙是非常重要的。对于平面周期排列的弹性超材料，人们已经进行了大量的研究，以探索具有优良带隙特性的超材料结构[12-14]。Badreddine等设计了一种在X和Y方向周期排列双面短柱的弹性超材料，运用有限元法计算得到了宽频完全带隙。Krushynsk等[16]研究一种含有橡胶包覆层的弹性超材料，通过平面周期布置晶格结构可得到起始频率低于200 Hz以下的低频带隙。Gao等[17]提出一种在X和Y方向周期分布双谐振腔的二维弹性超材料，在35 Hz左右可产生5 Hz宽的超低频带隙。但是，以上研究仅基于直角坐标系进行弹性超材料的带隙特性研究，对于柱坐标下的径向弹性超材料并未涉及。

径向弹性超材料是一种在径向方向上呈周期性排列的环形结构，具有全向带隙特性。Shi等[18]提出一种由有机玻璃和钢交替组成的径向弹性超材料，得到宽频完全带隙。Ma等[19]研究具有晶格滑移特性的双层径向弹性超材料，其结构呈现宽频完全带隙特性。Li等[20]设计一种基板由铝和环氧树脂交替组成，并且在基板上附加周期性的橡胶和钢块的径向弹性超材料，得到起始频率低于500 Hz带宽为100 Hz左右的带隙。Gao等[21]设计一种以钢为基体附加硅橡胶与钢组合质量块的径向弹性超材料，其一阶带隙中心频率存在于300 Hz附近。虽然径向弹性超材料以实现低频阻带为目标，但是仍然难以实现零频起始频率的阻带。同时，目前的径向弹性超材料实现的低频带隙往往较窄，难以满足复杂的工程应用环境。

研究发现，对周期性结构施加固定端约束[22]，可在超低频率范围内打开宽频阻带。Yao等[23]设计一种特殊的质量弹簧系统，通过对结构施加固定端约束，此系统可对0起始的一定频率范围内的弹性波进行有效衰减。Antonakakis等[24]通过对弹性板上的特殊点施加固定端约束，研究弹性板中弯曲波的屏蔽现象，发现点约束形式将使结构产生零频起始阻带，并通过傅里叶级数与高频均匀化理论[25]从数学角度研究零频起始阻带的产生原因。Yu等[26]通过对梁下基面施加固定端约束，同样发现结构产生0起始的阻带。Achaoui等[27]通过对其周期性结构底面施加约束，设计一种拥有零频起始阻带的宽频二维地震超材料，可有效衰减地震波。但是，以上约束状态的带隙研究均基于直角坐标系下的周期结构，并未对径向周期性结构开展相关研究。同时，其约束状态下的带隙机制并不清晰且未涉及超材料固有振动属性研究。

本文提出一种工字型单相径向弹性超材料，并计算其不同约束状态下的带隙特性。通过运用本征模可视化方法，分析零频起始带隙产生及其带隙拓宽原因。最后，研究几何参数对带隙特性的影响。本文提出约束作用下径向弹性超材料，可有效衰减零频起始的宽频径向振动，对超材料超低频减振等领域的工程用拓展具有重要的现实意义。

1 “工”字型径向弹性超材料结构

本文提出的工字型径向弹性超材料的单元晶格结构，如图1(a)所示，图1(a)中：用a为工字型单位晶格结构的腿宽，即晶格常数；h，d，e为工字型单位晶格结构的腰高，腰厚与平均腿厚。单位晶格径向周期排列形成超材料结构的方式，如图1(b)所示。图1(c)、图1(d)、图(e)分别为三种不同约束状态下的超材料结构，其中深色表示超材料结构被约束面。图1(c)为Z向上下基面均施加固定端约束(简称双面约束)的超材料结构；图1(d)为Z向单基面施加固定端约束作用(简称单面约束)的超材料结构；图1(e)为无固定端约束作用(简称无约束)的超材料结构。其中，本文提到的约束均为刚性接触而形成的固定端约束，忽略固定端接触面上存在的小位移变形。

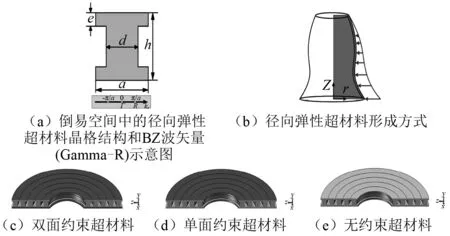
图1 径向弹性超材料 Fig.1 Radial elastic metamaterials

由于结构的特殊性，提出基于圆柱坐标系下的有限元方法来研究其超材料结构带隙特性。首先，建立圆柱坐标系下的弹性波动方程，以便计算无限系统中的色散关系曲线。其中：u,v,w分别为柱坐标系的位移分量；ρ为密度；t为时间；λ和μ为材料的弹性波常数；r,θ,z分别为柱坐标系下的坐标分量。

(1)

(2)

因其晶格单元的周期性结构是沿着径向方向无限的，根据Bloch定理，只需考虑单个晶格单元。其晶格的边界条件方程为

u(r+ra,z)=u(r,z)eikrra

(3)

式中：r为径向位置；a为晶格常数；kr为径向方向上Bloch波矢量Kr的分量。

利用等式(3)，在r上应用周期性边界条件，通过将Bloch波矢量Kr扫描第一不可约布里渊区的边界，可以得到径向超材料结构的色散关系曲线。

对于有限周期结构，需要计算频率响应函数曲线来描述其传输特性。通过在有限周期结构的一端沿径向方向施加柱面加速度/位移激励，同时在另一端记录其所产生的柱面加速度/位移响应，从而计算频响函数。

T=20lg(a2/a1)

(4)

式中：a1为激励端的加速度/位移激励；a2为拾取端的加速度/位移响应。

根据有限元理论[28]，式(1)可以转化为具有离散形式的广义特征值方程

(K-ω2M)u=0

(5)

式中：K为超材料结构的刚度矩阵；M为超材料结构的质量矩阵；u为特征向量。

在获得有限元广义本征方程式(5)后，通过给定一组Bloch波矢量Kr，在该波矢条件下计算单一晶格单元的各阶本征频率ω，并回代至有限元方程，即可求得各阶特征向量u=[u1,u2,…,un]T，继而依据特征向量建立晶格单元中各点的位移值，并通过差异化的颜色显示，即可获得单一晶格单元的本征模位移矢量场[29]。本文将采用这种有效的有限元方法研究弹性超材料的带隙特性。

2 数值结果与讨论

2.1 带隙结构分析

应用有限元法分别计算了三种不同约束状态下的超材料结构的色散关系曲线。其中，几何参数如下：晶格常数a=0.1 m，腰高h=0.1 m，腰厚d=0.06 m，平均腿厚e=0.02 m。整体结构的材料为钢，其杨氏模量E=2.106×1011Pa，泊松比μ=0.3，密度ρ=7 880 kg/m3。

图2、图3和图4分别为双面约束、单面约束和无约束状态下的超材料结构的色散关系曲线。由图可知，三种约束状态下的超材料结构均能产生完全带隙。由图2(a)可知，双面约束下“工”字型径向弹性超材料出现了零频起始频率，在30 000 Hz以下仅存在两条能带曲线，其第一带隙(0～16 849 Hz)位于第一条能带以下。单面约束状态下同样出现了零频起始频率，在15 000 Hz以下也仅存在两条能带，如图3(a)所示，其第一带隙(0～5 611.8 Hz)的截止频率与双面约束状态下相比降低较多，带隙宽度仅为双面约束带隙宽度的1/3。由图4(a)观察到，无约束状态下在20 000 Hz以下存在四条能带曲线，其中第一带隙(14 298～16 993 Hz)位于第三条和第四条能带之间，并不存在零频起始带隙。为了验证能带结构的正确性，分别对双面约束，单面约束和无约束状态下的8/16个周期超材料结构腰面加速度/位移信号拾取并进行平均处理，计算了超材料结构频响曲线，分别如图2(b)、图3(b)和图4(b)所示，可以观察到，加速度传输曲线与位移传输曲线存在较好的一致性，其带隙位置与色散关系曲线所得到的带隙结果相吻合。

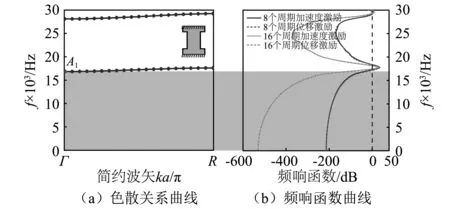
图2 双面约束超材料的振动带隙结构Fig.2 Vibration band gaps structure of metamaterial with double-sided constraints

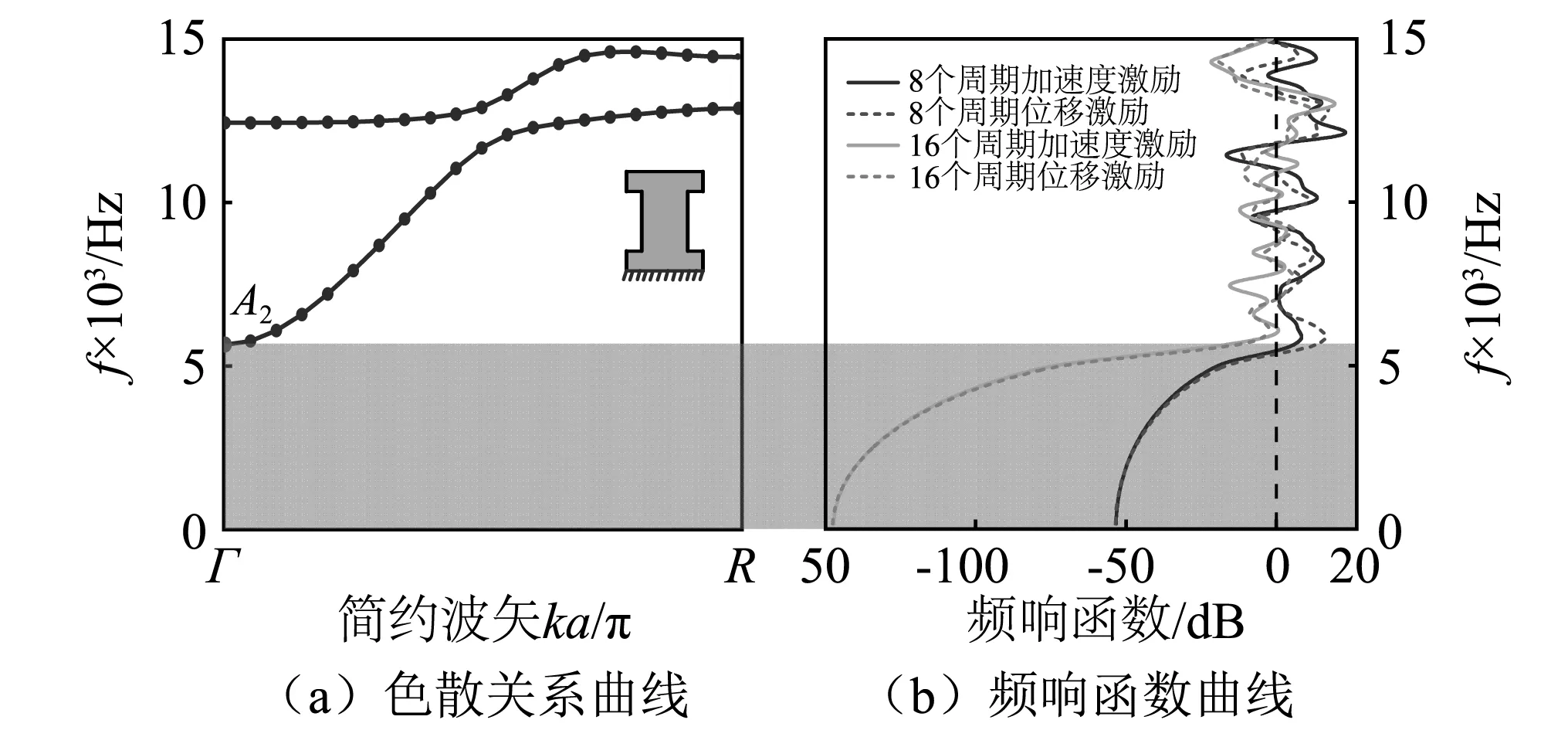
图3 单面约束超材料的振动带隙结构 Fig.3 Vibration band gap structure of metamaterial with unilateral constraints

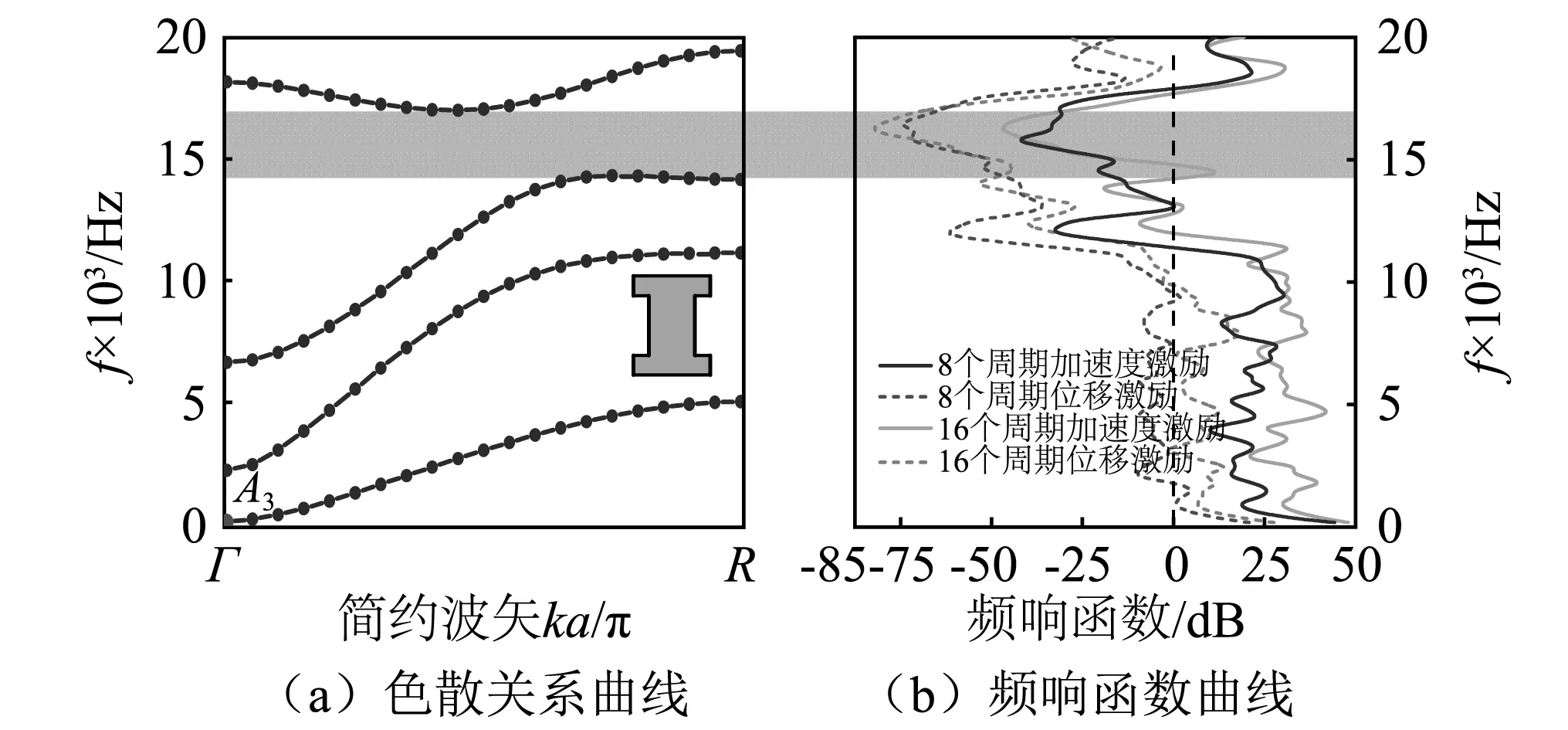
图4 无约束超材料的振动带隙结构Fig.4 Vibration band gap structure of metamaterial with unconstraint

2.2 带隙形成机制分析

为研究零频起始带隙的机制，分别计算了三种约束状态下能带特殊点的本征模位移矢量场，如图5所示。其中箭头代表振动位移的方向，不同深浅度代表振动位移的幅值。

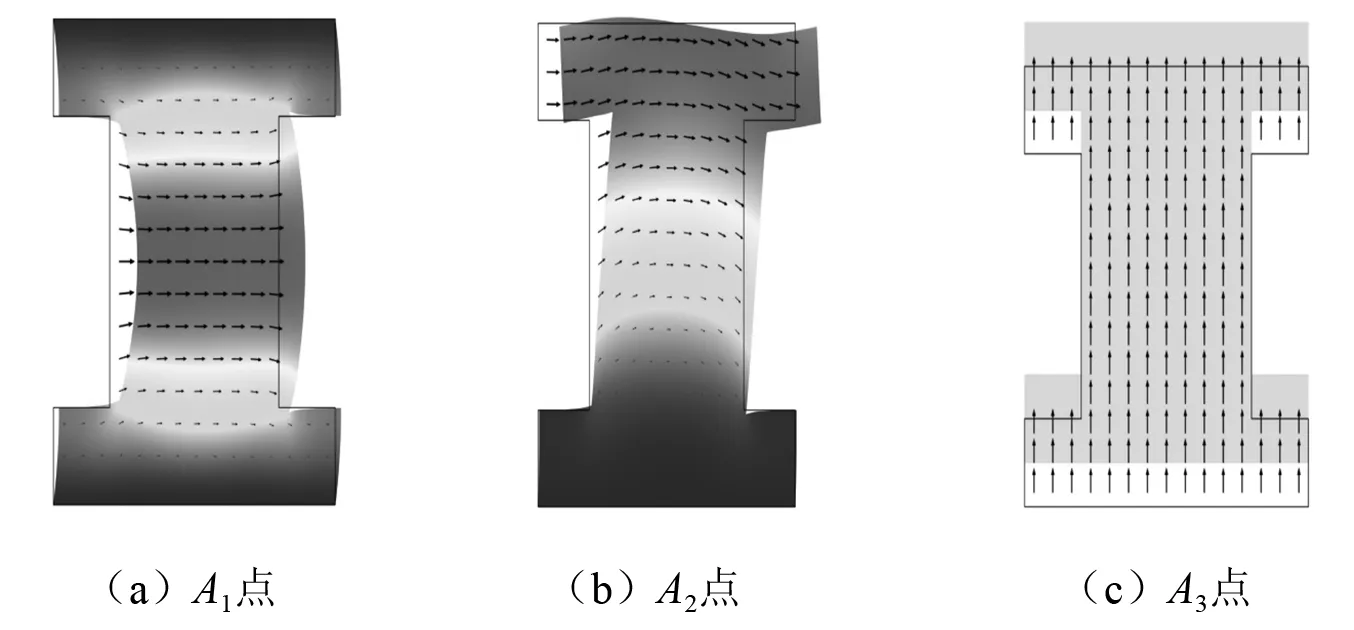
图5 不同约束状态下第一能带起始点本征模位移矢量场Fig.5 Eigenmode shapes and displacement vector fields of the first band at the starting point in different constrained states

可以观察到，A1点的振动模态集中在晶胞中部的径向振动，整体呈现局域径向振动模态，这是由于Z向上下两基面施加固定端约束导致振动无法在上下基面产生；A2点，由于Z向单面施加固定端约束，下基面保持静止，振动集中分布于晶胞上部，整体呈现类似“摆锤”的局域旋转振动模态；而A3点，由于上下基面无约束，因此振动均匀分布在整个晶胞各处，整体呈现轴向的垂直振动模态。因此，由于面约束的作用，引起结构固有本征模位移矢量场的改变，从而使超材料结构的局域振动打开零频起始带隙。

进一步，研究双面约束下超材料零频起始带隙有效拓宽的原因。由图5中A1和A2点的振动模态可知，双面约束和单面约束状态下的振动模态可分别等效为一个弹簧-质量系统[30]和一个弹簧-摆系统[31]。零频起始带隙的截止频率与结构在A1点，A2点的固有频率相关，其固有频率可以分别由下式确定

(6)

式中：Ke为等效弹簧的刚度；Me为等效质量。

(7)

式中：Ke为等效弹簧的刚度；J为结构惯性矩；l为等效弹簧与旋转中心的距离

A1点时，结构的等效质量Me(46.946)A2点(1.12×1011)。依据式(6)、式(7)，A1点的固有频率f将显著高于A2点。因此，约束状态的差异将产生不同的局域振动模式，双面约束超材料存在低的等效质量Me与高的等效刚度Ke，结构出现高的截止频率，这是径向弹性超材料零频起始带隙有效拓宽的主要原因。

2.3 零频起始带隙机制分析

进一步研究有限周期超材料结构的振动特性，探讨固定端约束状态下超材料结构零频起始带隙的产生机制。图6、图7分别表示8个周期的径向超材料结构在双面约束状态和单面约束状态下第一带隙中心频率处沿径向的位移场。在图6中，其双面约束状态下第一带隙中心频率为8 425.5 Hz，其入射波被有效反射，并出现局域振动模式；在超材料阵列内部，振动幅度在第一个晶格处最大，然后向出口呈指数衰减，在出口一侧观察到低透射率。第一晶格处的振动模式沿轴向方向是对称的,这与试验的结果是一致的[32]。因此，双面约束状态下8 425.5 Hz附近的全带隙明显与晶格的局部共振有关。同时，在单面约束2 805.5 Hz处，可观察到相同的现象，如图7所示。因此，固定端约束作用下径向弹性超材料产生的全带隙明显与晶格的局域共振机制有关。

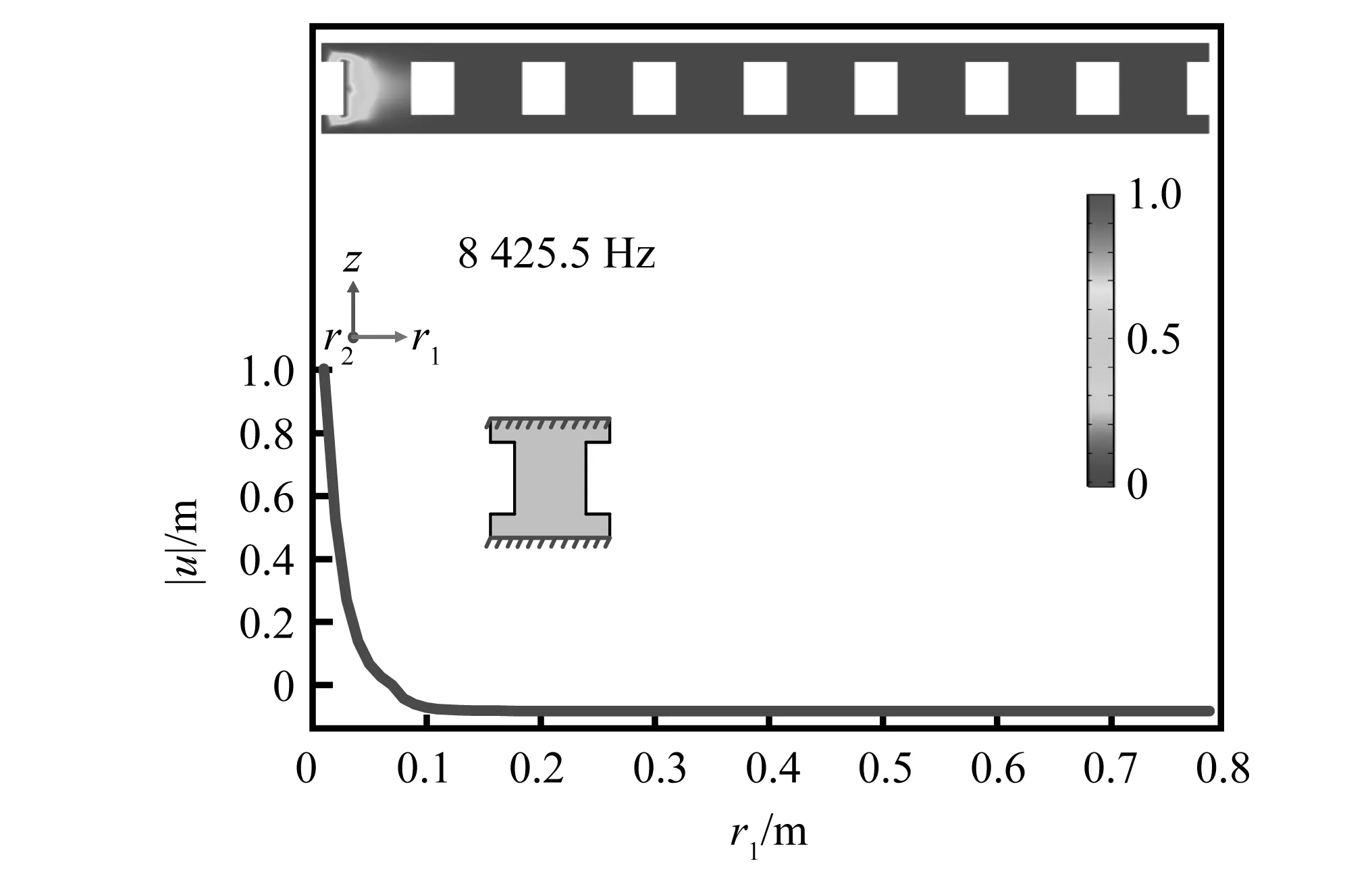
图6 双面约束超材料的径向振动位移场研究Fig.6 Investigation on radial vibrational displacement fields of metamaterial with double-sided constrains

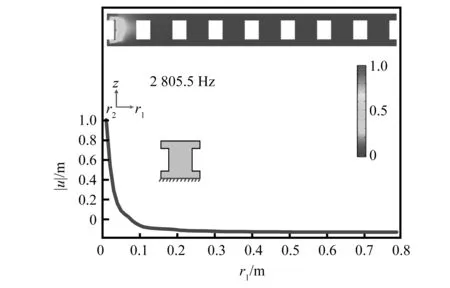
图7 单面约束超材料的径向振动位移场研究Fig.7 Investigation on radial vibrational displacement fields of metamaterial with unilateral constraints

3 几何参数对带隙特性的影响

本节研究几何参数对双面约束超材料的带隙特性的影响。图8(a)为第一带隙随几何参数比值d/a的变化规律，其中，材料参数及其他几何参数均保持不变。由图可知，随着d/a的增加截止频率呈现先逐渐升高而后缓慢下降的趋势，带隙宽度先变大后减小。当d/a=0.45时，零频起始带隙的宽度最大。由于双面固定端约束作用，工字型结构中部即作为提供等效刚度的弹簧，同时又作为提供等效质量的质量体(如图8(b)所示)。当d/a<0.45时，结构中弹簧作用将处于主导地位，随着参数d/a的增加，等效刚度Ke的不断增加，将是带隙宽度变大的原因。在参数d/a=0.45时，结构中部承担弹簧作用与质量体作用的比例相近，使其带隙宽度出现最大值。而后，随着参数d/a的增加，结构局域径向振动的加强，引起结构等效质量Me的增加，这将是其带隙宽度缓慢下降的原因。

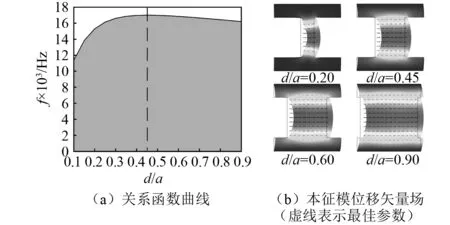
图8 带隙特性与参数比值d/a的关系Fig.8 Relationship between parameter ratio d/a and band gap characteristics

图9(a)为双面约束状态下径向弹性超材料带隙随几何参数比值e/a的变化。可以看出，第一带隙的截止频率值随着e/a的增加呈现单调增加趋势，其带隙宽度也逐之变宽。为了探讨带隙宽度变化的原因，计算了不同e/a的本征模位移矢量场(如图9(b)所示)。结果表明，随着e/a的增加，工字型结构的弯曲刚度不断增大，引起结构上下侧弯曲振动作用不断减弱，而结构局域径向振动逐步加强。结构上下侧与结构中部径向振动耦合作用的不断增强，是导致其截止频率不断升高，带隙宽度逐渐增加的主要原因。

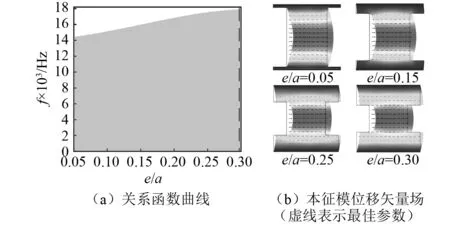
图9 带隙特性与参数比值e/a的关系Fig.9 Relationship between parameter ratio e/a and band gap characteristics

4 结 论

本文提出一种“工”字型径向弹性超材料，研究三种约束状态下的带隙特性及变化，并对其双面约束和单面约束状态下的零频起始带隙机制进行了分析，最后研究了随着几何参数的变化，双面约束状态下的“工”字型径向弹性超材料的零频起始带隙的变化规律。

研究表明：“工”字型径向弹性超材料的带隙特性受其结构固有振动属性的影响，约束作用将改变结构固有属性，影响结构的带隙特性；固定端约束使 “工”字型径向超材料结构具有零频起始带隙特性，并随着约束面的增加，有效拓宽了超材料结构的零频起始带隙的宽度；零频起始带隙的产生机制是局域共振机制,约束作用在布拉格散射周期性结构中形成局域共振模态，这是打开零频起始带隙的关键；随着参数比值d/a的增加，带隙呈现先变大后减小，其原因为工字型结构中部即提供等效刚度，同时又提供等效质量，等效刚度Ke与等效质量Me随d/a的动态变化是引起带隙变化的主要原因；随着参数比值e/a的增加，结构弯曲刚度增大，弯曲振动作用的减弱与径向振动作用的增强，促使带隙宽度逐渐变宽。

本文提出约束作用下径向弹性超材料，具有零频起始带隙，对于径向振动具有强烈的衰减特性，对超材料超低频减振等领域的工程应用拓展具有重要的应用前景。