束流位置探测器自动标定系统研制

唐旭辉 何 俊 岳军会 魏书军 杜垚垚 麻惠洲 刘 智 杨 静高国栋 曹建社 王安鑫 随艳峰 叶 强

1（中国科学院高能物理研究所 北京 100049）

2（中国科学院大学 北京 100049）

高能同步辐射光源（High Energy Photon Source，HEPS）建成后将是我国亮度最高，发射度最低的第四代同步辐射光源［1‒2］，HEPS的同步辐射光达到预期的品质，离不开束流轨道反馈系统对电子束流精确地测量和控制［3］。束流位置探测器（Beam Position Monitor，BPM）是束流轨道反馈系统的最前端元件，可以测量带电粒子束团质心的横向位置［4］，计算方法是用探头灵敏度系数Kx和Ky分别与归一化电压信号U和V相乘，其中U、V在BPM设计阶段有仿真值。由于加工公差、安装误差等因素存在，实际测量的U、V值与仿真值有一定差别［5］，而且，当束流位置远离探头机械中心时，位置坐标x、y与U、V有非常明显的非线性关系，此时用线性函数计算将无法得到准确的位置。因此，BPM在正式使用前需要进行标定，从而建立实测U、V与真实束流位置更加精确的映射关系，完成标定任务的工具就是BPM标定系统。中国科技大学国家同步辐射实验室设计了合肥光源储存环和直线加速器的BPM标定系统，用于BPM的标定与检验［6‒9］。中国科学院高能物理研究所基于BEPCII设计了一套自动标定平台，使标定后的条带BPM计算精度控制在10μm以内［10］。本文描述了一套高效率，高精度的自动标定系统的研制过程。利用该系统进行了BPM探头标定实验，自动采集足量的原始坐标数据和U、V数。对这些数据进行离线分析，获得了探头在不同条件下的标定系数，Mapping图和误差分布图。讨论了不同标定条件对BPM测量精度的影响，为BPM电子学的设计提供理论参考。

1 BPM自动标定系统总体硬件架构

标定系统硬件架构如图1所示，主要由模拟束流发生装置、机械运动机构、BPM信号处理电子学和工控机组成。信号发生器、放大器与高保线（Goubau Line，G-Line）组成的模拟束流发生装置向空间发射电磁场被BPM探头探测，产生4路电压信号传给BPM电子学进行处理，处理后的数据会通过实验物理与工业控制系统（Experimental Physics and Industrial Control System，EPICS）被工控机获取。BPM探头安装在二自由度精密移动台上，通过移动平台的精确定位，给出高保线在BPM坐标系中的真实位置。工控机是标定系统的控制中心，运行在其上的控制软件通过网络或串口给其他设备发送控制指令，保障各个子模块协同工作，并且将采集到的数据进行离线分析，生成报告。

图1 BPM自动标定系统架构图Fig.1 Schematic of BPM automatic calibration system

1.1 模拟束流发生装置

模拟束流发生装置利用信号源和天线产生TEM波（Transverse Electromagnetic Wave），模拟束流高速通过时形成的电磁场环境［11］。传统的标定系统多采用天线模拟束流。G-Line由于具有低损耗、宽频带、高传输效率、不需要复杂的阻抗匹配网络等优点，近年来已被多个研究机构用作束流模拟装置来辅助测量加速器射频器件的耦合阻抗［12‒13］、标定积分流强变压器［14］等。本文设计的G-Line系统，信号线是一根涂敷薄绝缘层的导线，信号线两端连接在锥形喇叭的中心，G-Line的示意图［15］和实物图如图2所示。在499.8 MHz、15 dBm正弦信号激励下，探头耦合的4路信号幅值之和比纯金属丝天线约提高2.7倍。为使探头耦合的信号足够强，满足电子学测量分辨率的需求，在信号源和G-Line之间加入增益为30 dB的射频放大器。

图2 G-Line的示意图(a)和实物图(b)Fig.2 Schematic diagram(a)and physical picture(b)of G-Line

1.2 机械运动与支撑装置

纽扣型BPM安装在二自由度运动平台上，运动平台固定在可以自动调平，并具有隔振能力的气动阻尼实验台上，避免地面随机振动或人为走动造成天线抖动产生信号毛刺，实验台和运动平台如图3（a）所示，地面与实验台的振动差异如图3（b）所示［16］，隔振效果显著。运动平台采用日本西格玛光机生产的HST-XYZ（SG）系列，重复定位精度为0.5μm，最小步距为2μm，光栅尺理论分辨率为0.05μm，在两个自由度的移动范围均为±50 mm，保证了标定结果的精度、准确性以及扫描范围的全面性。为了减小仪器设备因热变形引起的误差，实验环境为恒温（25±0.1）℃。

图3 支撑装置(a)与除振效果图(b)Fig.3 Support device(a)and vibration removal effect(b)

1.3 BPM信号处理电子学

BPM探头与BPM信号处理电子学组成数字BPM系统，电子学首先对模拟信号进行调理，经ADC转换后计算出差和比信号，再按不同频率抽取出逐圈数据，快反馈数据和慢反馈数据［17］。慢反馈数据又称闭轨数据，是本文的主要研究对象。为完成BPM探头的标定任务，对电子学的性能提出较高要求，本文选用较为先进的Libera Brilliance+BPM电子学，其闭轨位置分辨率为20 nm，温度漂移为0.2μm·℃−1，可调衰减范围达31 dB。电子学的微控制器搭载Linux操作系统运行EPICS输入输出控制器（Input Output Controller，IOC），将计算的闭轨数据打包传入网络最终被上位机获取。

2 BPM自动标定系统的软件设计

标定系统软件包括控制程序、数据获取程序和离线数据分析程序，所有程序运行在Linux系统。其中控制程序和数据分析程序用Python语言编写。

2.1 控制程序

控制程序主要完成对信号发生器和运动平台的控制，其GUI界面和流程图如图4所示，GUI包含串口号、波特率下拉菜单；运动起点坐标、运动步长、标定点数目、扫描方式、RF信号输入框；扫描方式二选一开关；串口开启/关闭、4方向单步运动等组件，来完成系统的初始化工作，标定开始后，BPM每走一步，都会将实际位置，计算位置，归一化电压等信息写入一个.csv文件。GUI程序与写有运动指令发送、仪器控制、回归分析、制图制表等函数的脚本文件保存在一个PyCharm的项目中，方便相互的导入和调用。控制程序的开发主要使用Python3的visa库，serial库和tkinter库分别实现SCPI命令的发送，串口通信和GUI编程。

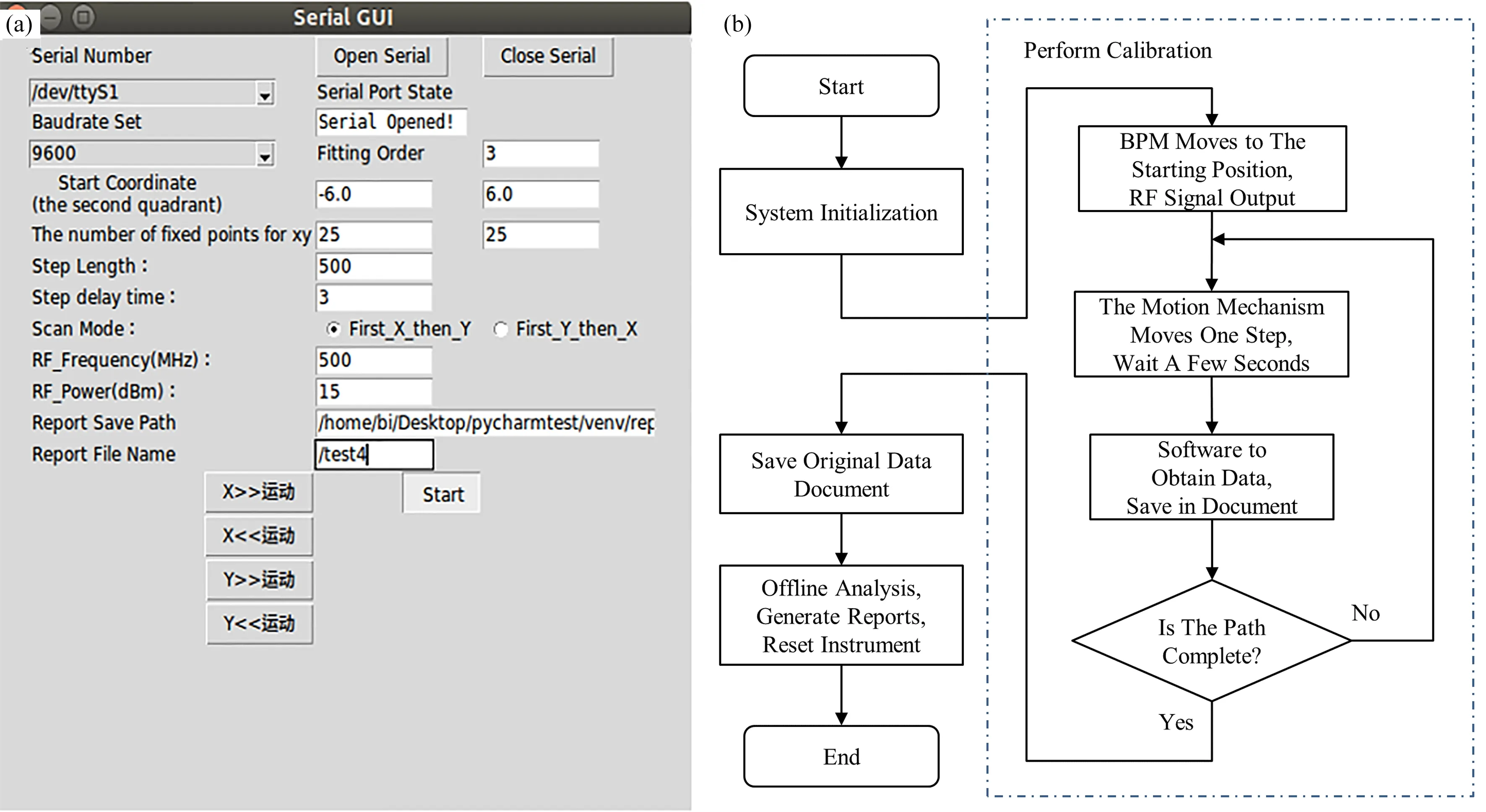
图4 控制程序的GUI界面(a)和流程图(b)Fig.4 Graphical user interface(a)and flow chart(b)of the control program

2.2 数据获取程序

BPM自动标定平台采用EPICS的通道访问接口实现数据的获取。EPICS是基于客户端/服务器模型的分布式控制软件框架，其结构如图5（a）所示［18］。EPICSIOC是一个常驻被控设备内存的分布式实时数据库，运行在电子学的嵌入式系统中，采集电子学的数据。客户端通过CS-Studio软件开发操作界面（Operator Interface，OPI）程序，实现过程变量（Process Variable，PV）的动态显示，也可通过Python的pyepics库来获取某一时刻的PV值。本文使用的Libera电子学OPI界面如图5（b）所示。

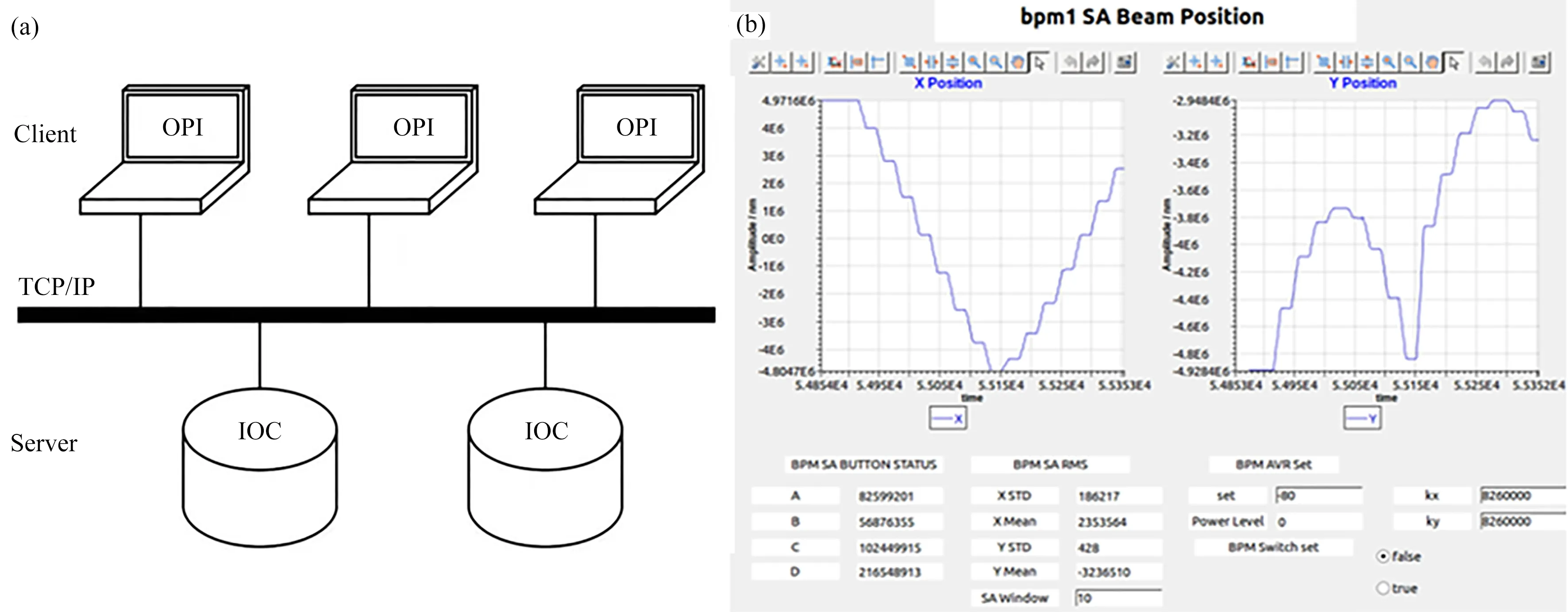
图5 EPICS架构图(a)和OPI显示界面(b)Fig.5 EPICSarchitecture diagram(a)and OPIinterface display(b)

2.3 离线数据分析程序

纽扣型BPM的4个感应电极交叉分布在管壁上，电极的命名和坐标系的定义要与电子学的信号处理算法相匹配。本文束流测量坐标系以及该坐标系下束流位置与电压信号的关系如图6所示。

图6 中U和V是按照和差比方式定义的归一化电极信号，Kx和Ky为束流测量的灵敏度或探头标定系数。当束流位置靠近BPM机械中心时，x和y分别是U和V的线性函数，满足该关系的这片中心区域被称为线性区，但是在非线性区，x已不是U的线性函数，甚至不只是U的函数，还可能依赖于V，y也同理。因此，为了在全部范围内建立归一化U和V与坐标x和y的映射关系，现假定x和y分别是U和V的二元n阶多项式函数［3］，即：

图6 BPM坐标系及位置计算式Fig.6 BPM coordinatesystem and position calculation formula

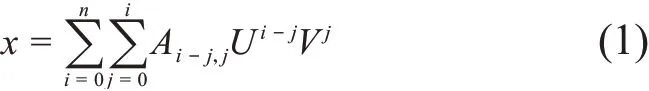
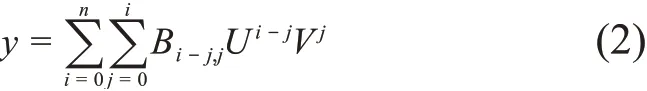
多项式的阶数n与项数N的关系为N=n(n+3)/2+1。当n为1时，x、y即是U和V的线性函数，适用于标定小直径或者束流运动范围不大的BPM。适当提高n有利于提高拟合精度。方便起见，将式（1）、（2）写成向量相乘的形式：

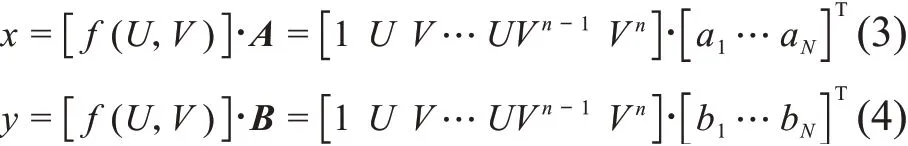
下面以x为例简述拟合算法，假设标定点的个数为M，这些点横坐标的拟合值组成向量X=[x1x2…xM]T，那么有：将式（5）简写为X=FA，F为归一化U和V组成的M×N的矩阵。由最小二乘法，全部标定点横坐标真实值与拟合计算值的误差平方和为：

其中：X0=[x01x02…x0M]T是全体标定点横坐标的真值组成的向量，由精密运动机构在扫描时停驻得到。式（6）表明，EX是A的函数，问题变成：寻找一个合适的向量A，使EX最小。根据矩阵求导法则：∂EX∂A=2FT(FA−X0)=0。从而得到FTFA=FTX0。由于FTF是满秩矩阵，因此A=(FTF)−1FTX0。同理，y方向的拟合系数向量B=(FTF)−1FTY0。其中Y0=[y01y02…y0M]T是全体标定点纵坐标的真值组成的向量。有了A和B，就可以按照式（1）来设计电子学，从而在加工误差和非线性效应存在的情况下准确计算出位置坐标。单个方向的拟合的效果用均方根误差（Root Mean Square Error，RMSE）衡量，在全体标定点上，多项式拟合的均方根误差为：

由于系数向量A和B本身是由标定点训练得到的，因此标定点的均方根误差不足以反映数学模型（式（1）或式（5））的好坏，需要构建测试集Xt和Yt，对应Ut和Vt构成的矩阵为Ft，测试点的数目为Mt，多项式拟合在测试点的均方根误差为：

3 标定实验

3.1 原始数据采集

为验证该标定系统能否实现预期功能，选择内径20 mm的纽扣BPM进行标定试验。要得到探头标定系数向量A和B，需要先采集位置数据X0、Y0以及每个位置的归一化电压信号U和V。考虑到信号线直径和准直误差等因素，选择以BPM中心为圆心、半径为9.5 mm的圆作为数据采集区域（占BPM面积的90%），在边缘留有0.5 mm的裕量。设定每个点的间距为0.25 mm，启动自动标定程序，采集到的原始坐标数据处理前后的Mapping图如图7所示。

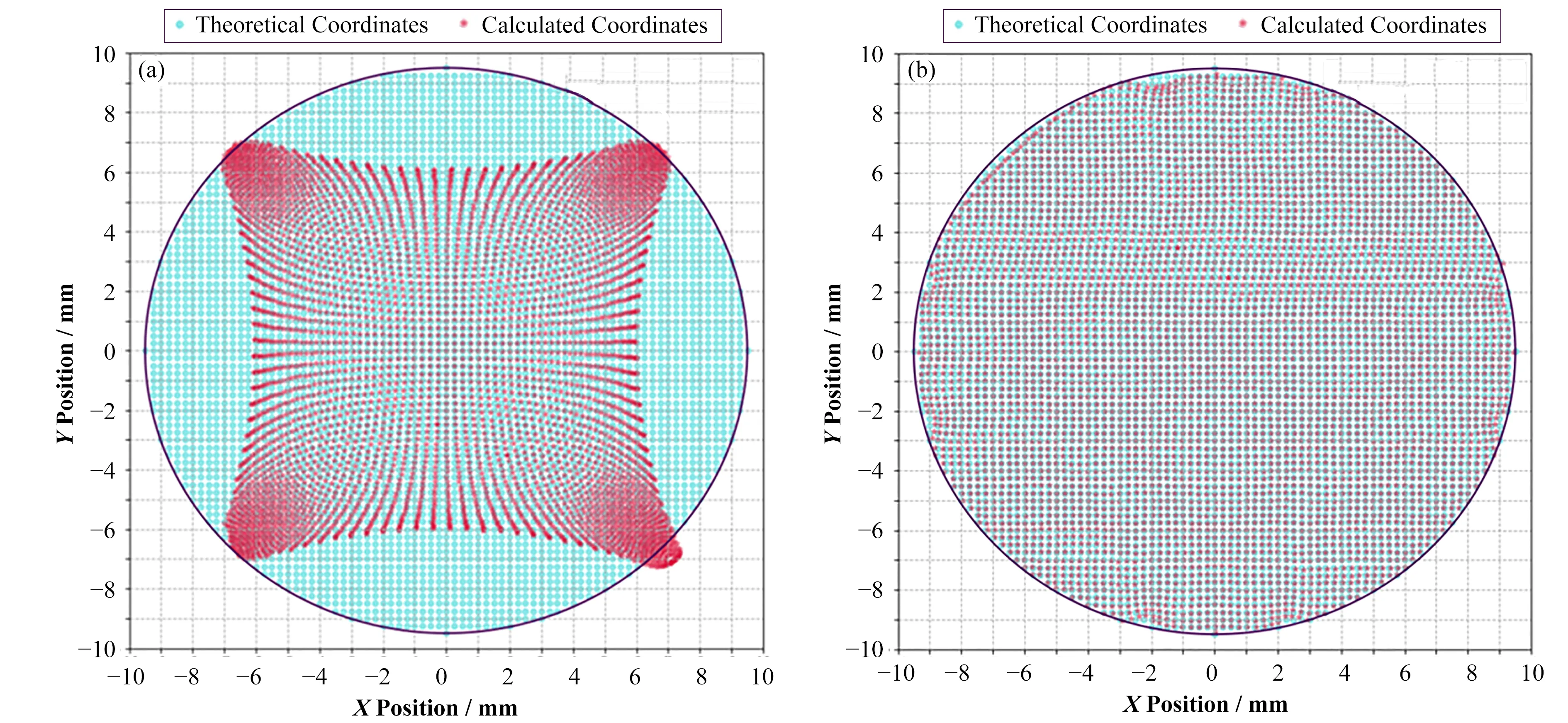
图7 标定前(a)和标定后(b)在半径9.5 mm圆内的理论坐标和计算坐标Fig.7 Theoretical and computational coordinatesin the9.5 mm-radiuscircleof pre-calibration(a)and post-calibration(b)

由图7（a）可看出，按照x=KxU和y=KyV计算得到的坐标，仅在中心约半径2 mm的线性区内与实际符合较好。越是远离线性区，尤其是在±45°的方向，误差越大，这是因为BPM的电极是45°配置，当信号线靠近某一个电极时，由于该电极耦合的电压信号过大，导致电子学上该通道的ADC饱和，U和V不再随信号线位置而显著变化。图7（a）计算点构成的阵列不完全对称，表明电极具有加工误差。BPM线性区的面积约仅占整个BPM面积的4%，要想在更大范围提高BPM的计算准确度，需要使用多项式算法。

3.2 标定系数的确定与误差分析

在采集的原始数据中，筛选出一部分作为标定点，用来确定多项式系数向量A和B，其余作为测试点，用来评估数学模型的好坏。多项式拟合的效果与选定的束流活动区域，标定点的数目和密度，多项式拟合的阶数均相关。本文选择以原点为圆心，半径（R）分别为3 mm、6 mm和9 mm的圆作为束流活动区域。用三种方式选取标定点，其中方式1标定点的横纵坐标均为奇数，如（1，−3）；方式2标定点的横纵坐标均为整数，如（−4，7）；方式3标定点的横纵坐标均为0.5的倍数，如（2.0，3.5）或（−1.5，3.0），显然，方式2的坐标点集包含方式1，方式3的坐标点集包含方式1和方式2。以1~11为多项式拟合阶数。将上述条件进行组合，用程序进行若干次试验，求得每次试验测试点的均方根误差。图8展示了以方式3选取标定点，不同活动半径和阶数下的测试点均方根误差，以及设定活动半径为9 mm，不同标定点选择方式和阶数下的测试点均方根误差。

从图8（a）可看出，R越大，需要更高的拟合阶数才能降低误差。当R较小，过高的拟合阶数会造成过拟合。图8（b）表明，提高标定点的数目和密度，对提高拟合精度影响较小。方式1阶数大于7后，误差回升，而方式2和方式3继续下降，表明标定点的密度要与模型复杂度相匹配，较少的标定点设置较高的阶数，容易造成过拟合。在R=9 mm的范围内，选择方式3、阶数为11来进行标定，精度最高，此时x、y方向测试点的均方根误差分别为39μm和17μm，拟合前后计算坐标与实际坐标（包含标定点与测试点）的距离偏差如图9所示。

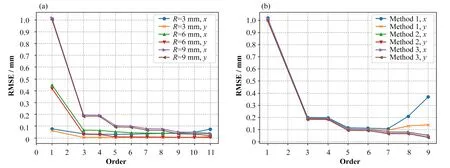
图8 方式3下不同半径和阶数的拟合误差(a)和在R=9 mm的范围内不同方式和阶数的拟合误差(b)Fig.8 Fitting errorsof different radiiand ordersin method 3(a),and different modesand ordersin therangeof R=9 mm(b)

图9 拟合前(a)和拟合后(b)的计算坐标与真实坐标的偏差Fig.9 Deviation between calculated coordinatesand real coordinatesbefore(a)and after(b)fitting

图9 （a）是标定前在边长为12 mm的正方形内计算坐标与实际坐标的距离偏差分布。显然，在边缘尤其是45°的地方，偏差较大。同样的区域，标定后的偏差如图9（b）所示，坐标轴的范围显示标定后的偏差比标定前整体小了两个数量级，约控制在0.15 mm以内。可以看出，经过标定后的BPM在很大范围内，计算坐标已非常接近于理想坐标。同时，组合试验发现，当活动范围选在R=2 mm的圆内，用方式3选择标定点，阶数在4~6时，x、y方向的均方根误差可控制在7μm以内。

4 结语

本文针对高能光源部分BPM标定需求，设计了BPM探头自动标定系统，开展了BPM探头标定实验。实验表明：该标定系统满足功能需求。使用该系统采集了BPM探头的U、V数据，并对原始数据进行分析，研究标定点的数目和密度，标定范围，多项式拟合阶数等因素对拟合精度的影响。标定范围越大，需要更多的标定点数和更高的拟合阶数，来描绘非线性物理场的数学模型，以减小拟合误差。拟合均方根误差在R=9 mm范围内小于40μm，在R=2 mm的范围内小于7μm。

作者贡献声明唐旭辉负责系统控制程序及算法的设计，以及文章的撰写和修订；何俊负责BPM样机和G-Line的设计；岳军会负责论文的修改；魏书军负责论文的修改；杜垚垚负责资料的搜集和整理；麻惠州负责BPM电子学的调试；刘智负责资料的搜集和整理；杨静负责资料的搜集和整理；高国栋负责资料的搜集和整理；曹建社负责论文的修改；王安鑫负责BPM样机的加工；随艳峰负责研究的提出及论文的修改；叶强负责系统的总体设计及软硬件环境的搭建。