改进型滑模扰动观测器的感应电机控制系统

袁庆庆，瞿汉飞

(上海理工大学 机械工程学院,上海 200093)

感应电机具有体积小、质量轻、惯性小、高转矩、鲁棒性好等优点，近年来在大型机床、农业生产机械、日常家用电器等不同场合得到广泛应用[1]。传统的感应电机转速伺服系统多采用线性控制理论，由于实现简单而被广泛应用[2]。然而，PI(Proportional-Integral)调节技术依赖准确的系统数学模型。当系统受到外部转矩突变扰动时，会导致传统的PI控制系统无法获得理想的控制效果[3]。在一般的工业应用中，负载扰动的影响可以忽略不计，但在一些对精度要求高的场合下负载扰动影响无法忽略，例如高性能数控机床等[4]。因此，提高感应电机在负载扰动下的控制性能，具有一定的理论研究和实际价值。

近年来，研究人员提出了许多非线性控制方法来改善感应电机的抗干扰能力，包括模型参考自适应控制[5]、二自由度PI控制[6]、滑模控制[7]、预测控制[8]、基于扰动观测器控制[9]等。在上述非线性控制方法中，基于扰动观测器的控制是一种被广泛应用于电力系统、航天航空和数字控制机床的先进控制理论，也被认为是消除扰动的最优控制方法。文献[10]提出了一种新型的转速观测器，通过电机动态方程建立滑模观测器模型，再根据李雅普诺夫稳定性原理，推导出系统收敛条件，从而估算得出转速值。文献[11]设计了一种负载转矩观测器，将观测结果反馈给速度环，并通过滑模控制方法对速度环进行控制，有效抑制了系统抖振，提高了系统的鲁棒性。文献[12]利用模糊逼近算法设计了扰动观测器，用来补偿未知输出饱和度、粘滞系数和负载转矩引起的扰动。基于滑模算法的扰动观测器观测效果良好，但也存在固有缺陷。当系统状态达到滑模面后，无法严格地沿着滑模面向平衡点滑动，从而产生抖振现象，不利于系统运行。因此，近年来提出了一系列克服抖动的方法，例如连续控制、高阶滑模面和新型趋近律的设计等[13-14]。抖振现象是系统状况轨迹对滑模面趋近结果不理想造成的，而滑模控制系统的关键在于抑制其抖振现象。合理的趋近律设计可以有效抑制抖振现象。文献[13]提出了一种趋近律，可以通过减小增益或使不连续增益成为滑模表面的函数来抑制抖动。文献[14]提出一种新颖的指数趋近律来设计速度和电流集成控制器，为了抑制抖动问题，在该趋近律中使用了系统变量。

为了提高感应电机速度控制的负载转矩抑制能力，并解决传统滑模控制的抖振现象，本文提出了一种改进型滑模扰动观测控制器。其可以准确估计系统负载转矩，然后将估计的转矩用作PI控制器的前馈补偿，以抑制由外部负载转矩变化引起的速度波动。此外，提出的改进型趋近律不仅可以确保估计的负载转矩快速收敛，还可以消除传统滑模控制结构的抖动。

1 感应电机数学模型及控制策略

1.1 数学建模

为简化分析，在建立感应电机数学模型时需要做出理想化假设，然后通过坐标变换理论，建立感应电机在同步旋转坐标系d-q轴下的数学模型[15]。

在同步旋转d-q参考系下，感应电机的磁链方程可表示为

(1)

式中，ψsd、ψsq分别表示定子磁链d、q轴分量；ψrd、ψrq分别表示转子磁链d、q轴分量；Ls、Lr、Lm分别表示定子电感、转子电感和互感；isd、isq分别定子电流d、q轴分量；ird、irq分别表示转子电流d、q轴分量。

感应电机电压方程如式(2)所示

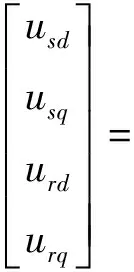
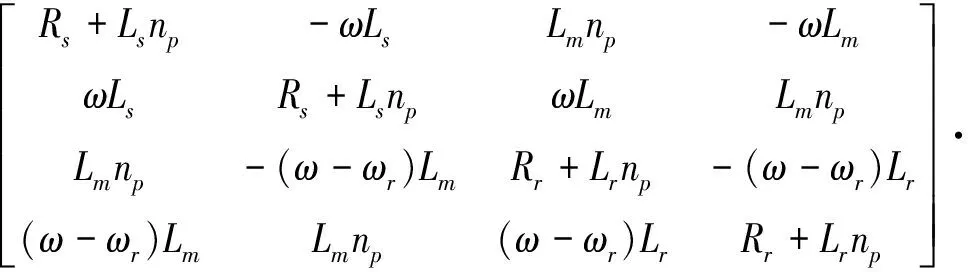
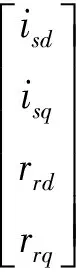
(2)

式中，usd、usq分别表示定子电压d、q轴分量；urd、urq分别表示转子电压d、q轴分量；ω表示机械角速度；ωr表示电机转子角速度；np表示极对数。

在外部负载下，感应电机的机械动力学方程为

(3)

式中，TL为负载转矩；J为转动惯量；B为黏滞系数；Te为电磁转矩。

电磁转矩方程可写为

Te=npLmλr/Lr·isq

(4)

令kt=npLmλr/Lr。式中，λr为转子磁通；kt为感应电机转矩系数。

1.2 基于FOC的控制策略

转子磁链定向控制(Field Oriented Control，FOC)是最常见的电机控制策略之一。基于FOC的感应电机控制框图如图1所示，包含了电流环和速度环两个PI控制环节[16]。

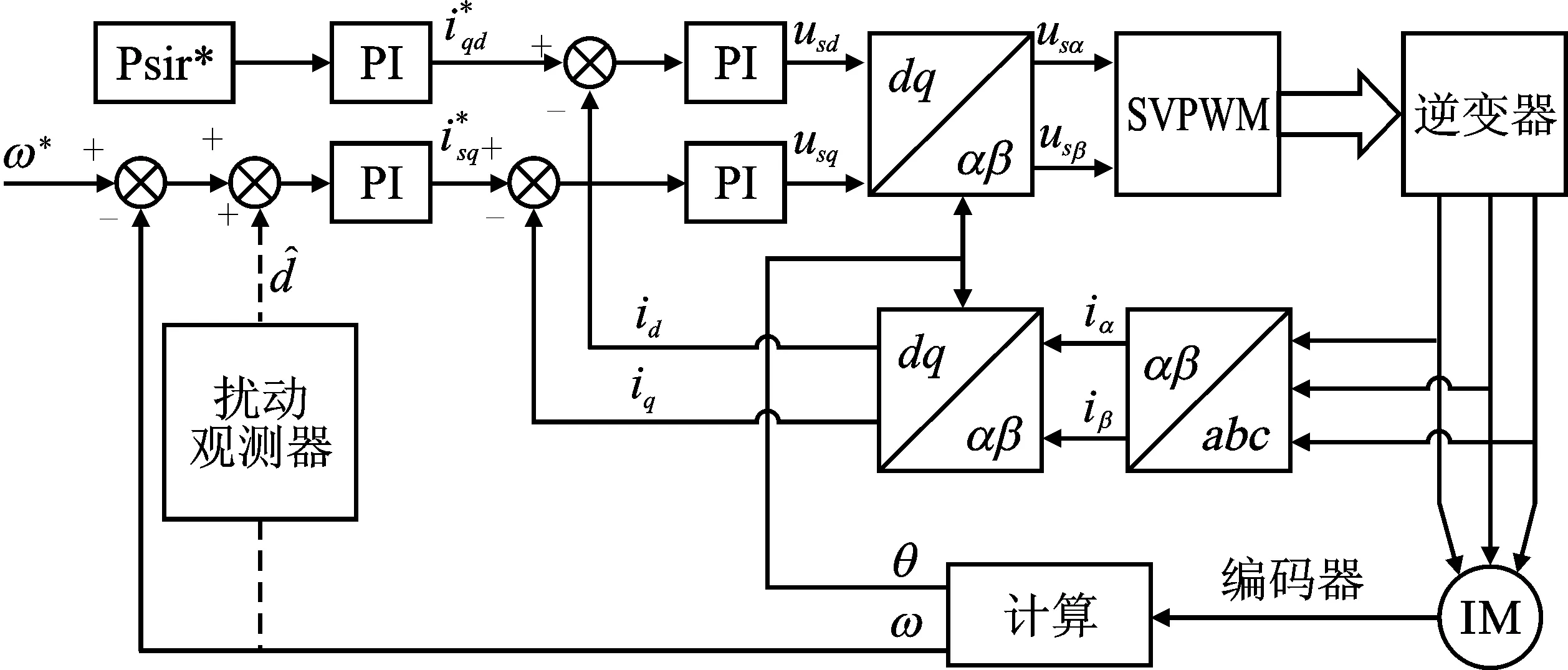
图1 基于FOC感应电机控制框图

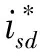
PI控制器的数学表达式为

(5)

式中，Kp为比例系数；Ki为积分系数。

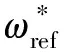
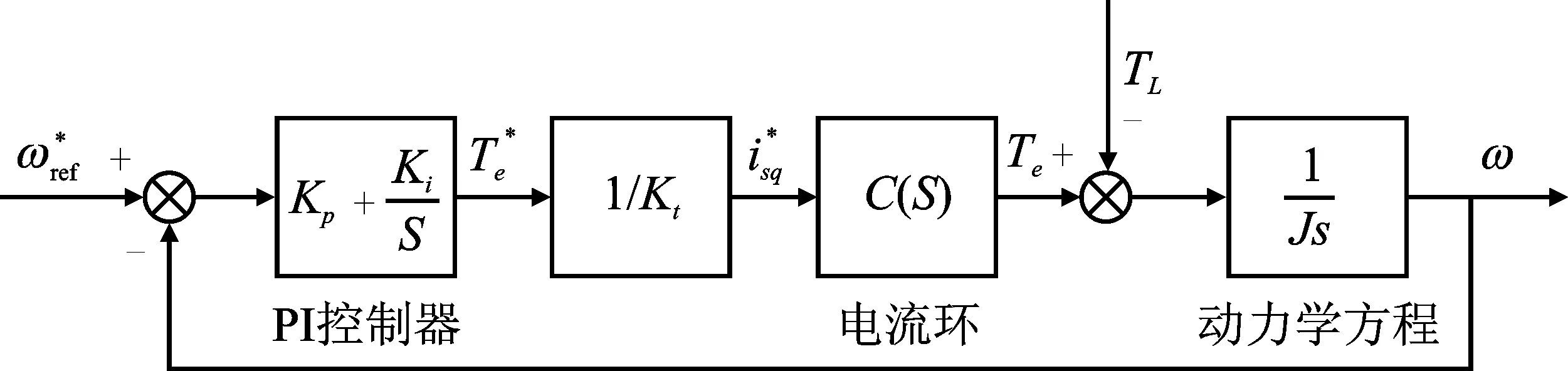
图2 基于PI控制的速度环的简化图

2 PI控制器的局限性及传统趋近律的缺陷

2.1 传统PI控制器的局限性

在图2的简化图中，电流回路传递函数C(s)可以表示为

(6)

式中，1/Tc表示电流环带宽。

所以，根据式(5)和式(6)，系统开环传递函数可表示为式(7)。

(7)

传递函数对应的Bode图如图3所示。

图3 系统传递函数波特图

其中，ωc是速度环的截止频率。系统截止频率随着ωc增大而增大，这意味着实现了快速响应[17]。然而，过大的ωc会产生大的过冲，导致系统不稳定。因此，ωc的选取会使系统响应速度和稳定性之间相矛盾，形成了传统PI控制器的局限性。

在电机仿真中，给定转速1 000 r·min-1时，外部负载(6 N·m)在0.5 s突加和0.7 s突减时的起动转速和负载转速仿真波形如图4所示。

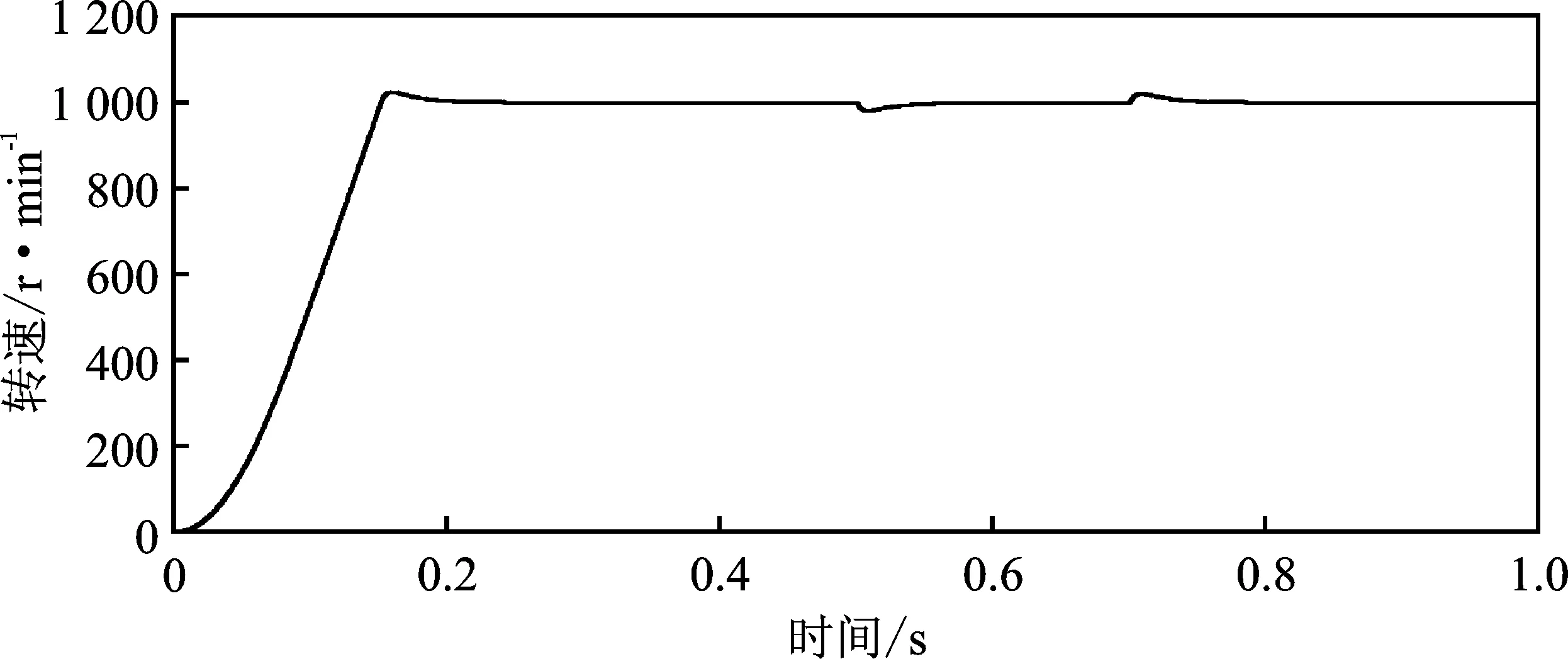
图4 起动时的转速波形和加减载时的转速波形

由图4可以看出，传统双PI下感应电机的转速性能较差，起动时间较长且超调量较大，外部负载加入时转速波动较大，恢复速度较慢。因此，研究外部扰动对电机转速性能的影响具有一定的实际意义。

2.2 传统滑模观测器趋近律的缺陷

扰动观测器有不同的设计方式。与其它方法相比，滑模控制以其较短的趋近时间和良好的鲁棒性而被广泛应用。

通常采用以下二阶控制系统来描述一种滑模控制系统[18-19]，表达式如式(8)所示

(8)

式中，x1和x2为系统状态；b为系数；u为控制量；d(x)为系统扰动项。

滑模控制设计的第一步是选取合适的滑模面。相对于比例滑模面，积分滑模面具有减小系统误差的优点，所以选择积分滑模面为

s=cx1+x2

(9)

式中，c为积分系数。

接下来，对趋近律进行选择，传统的趋近律表达式如下：指数趋近律

(10)

幂次趋近律

(11)

式中，ε为切换增益；η为线性增益(ε>0，η>0)。

传统的指数趋近律在系统趋近于滑模面时存在着趋近速度和滑模抖振程度相互耦合的缺点，证明过程如下：由式(9)和式(10)可得

(12)

将式(8)代入到式(12)可得

u=b-1[-cx2-d(x)-εsign(s)-ηs]

(13)

从式(12)可以看出，控制输入中存在着开关项-b-1εsign(s)，这将导致滑模抖振现象。

通过将式(9)对时间进行积分，得出到达滑模表面所需的时间t为

(14)

可以看出，趋近阶段运动时间与参数ε成反比关系，如果增加ε的值，可以获得更快的到达时间和良好的鲁棒性。但是，较大的ε值将导致滑模抖振程度加大。这种情况下，趋近速度与抖振程度由于同时与ε有关而相互制约。

3 基于改进型滑模观测器的扰动前馈补偿

3.1 改进型趋近律的提出

为解决上述问题，提出了一种改进型的指数趋近律，其表达式为

(15)

式中，η>ε>0。

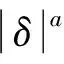
(16)

其离散表达式为

s(n+1)-s(n)=-ε|δ|αTsign(s)

(17)

式中，T为采样周期。假设系统轨迹在有限时间内达到滑模表面，则s(n)=0+或s(n)=0-。

若系统状态从s<0一侧进入滑模面，即s(n)=0-，则在下一个采样周期

s(n+1)=ε|δ|αT

(18)

若系统从s>0一侧进入滑模面，即s(n)=0+，则在下一个采样周期

s(n+1)=-ε|δ|αT

(19)

可得改进型趋近律引起抖振的切换面宽度为

Δ=ε|δ|αT

(20)

同理得出传统指数趋近律引起抖振的切换面宽度如式(21)所示。

Δ=εT

(21)

由式(20)和式(21)可以看出，传统指数趋近律的切换宽度与切换增益ε有关且是不变的，而改进型趋近律的切换面宽度会随着|δ|α减小而减小。两种趋近律的状态轨迹如图5所示。

(a) (b)

3.2 扰动观测器的设计

为了改善感应电机速度环对负载转矩的抑制能力，本文提出了一种改进型扰动观测器技术，如图6所示。扰动观测器通过对外部负载扰动进行在线估算，并将估算值用作PI控制的前馈补偿。改进型扰动观测器的原理描述如下。

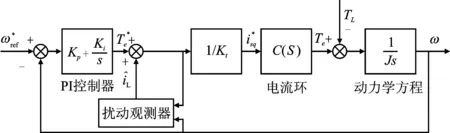
图6 基于改进型PI控制的速度环简化图

在感应电机伺服系统中，将电磁转矩Te和机械角速度ω作为输入，估算出外部转矩扰动TL。由感应电机数学模型中的式(3)得出

(22)

则增广状态空间方程如下所示

(23)

式中，λ是负载转矩TL的导数。在实际的感应电机控制系统中，负载扰动转矩TL的变化与其它系统状态信号有所不同，其在速度环采样周期内变化较为缓慢，可以将其一阶导数看为零。

将外部扰动TL作为状态变量，电磁转矩Te作为系统输入，机械角速度ω作为系统输出，则负载转矩观测器的状态方程可以设计为

(24)

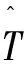
Q=LP

(25)

式中，L为观测器增益。图7为滑模扰动观测器结构框图。

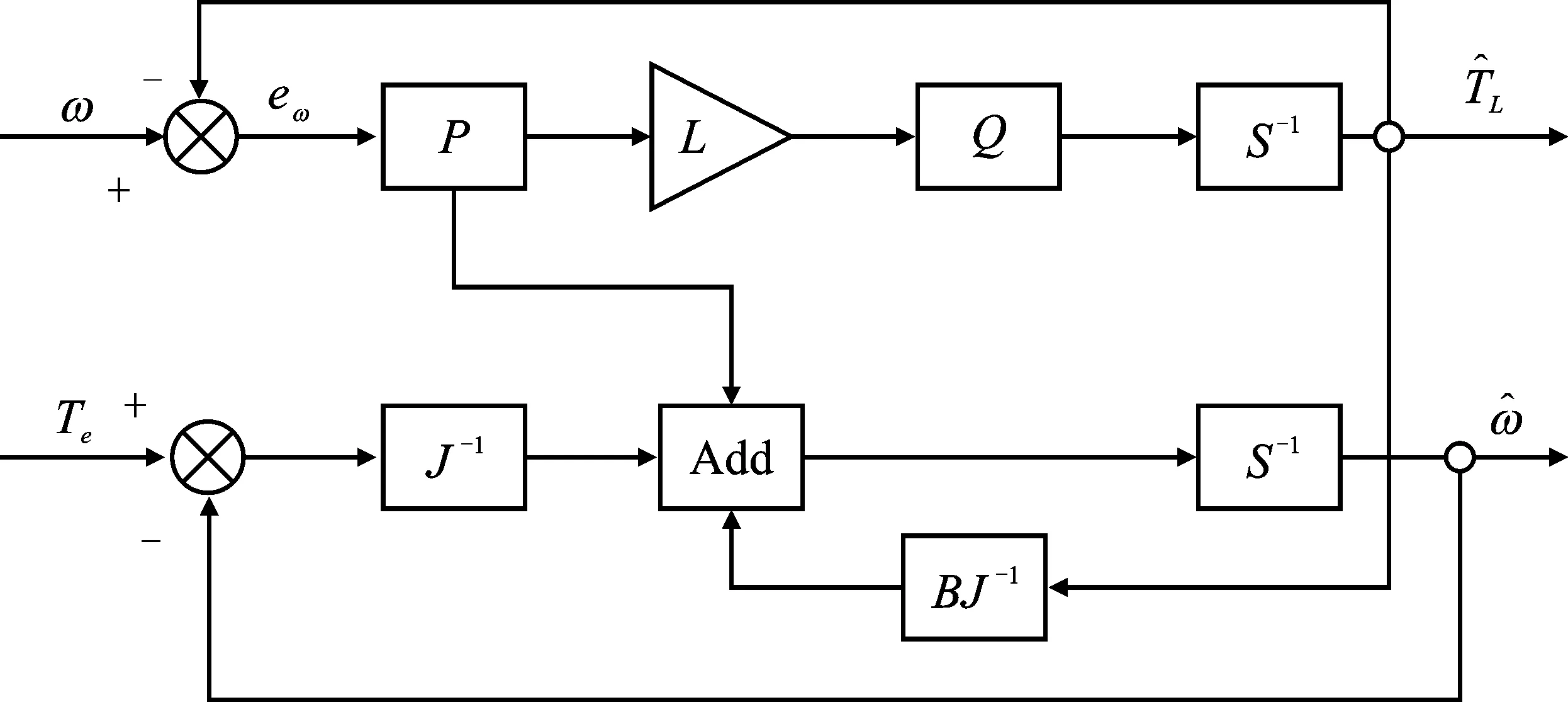
图7 滑模扰动观测器结构框图

通过式(23)减去式(22)，可以得到系统的误差状态方程

(26)

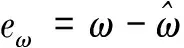
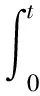
(27)

式中，cω为积分系数，且cω>0。

为了减少传统趋近律对系统产生的抖振现象，采用改进型趋近律，其表达式如式(15)所示。采用改进型趋近律对观测器的滑模控制律P进行设计，有

(28)

(29)

(30)

利用李雅普诺夫函数分析改进型扰动观测器的稳定性，定义李雅普诺夫函数为

(31)

时间t的导数可以由下式给出

(32)

将式(28)代入式(32)得到

(33)

(34)

因此，当切换增益εω的条件满足式(34)时，则表示采用此控制律的滑模扰动观测器是稳定的，系统可以在有限时间内收敛到滑模表面，并在此后的时间内保持不变。

4 实验结果分析

4.1 实验装置

为了验证所提出算法的可行性和有效性，在实验室中建立感应电机(Induction Motor，IM)速度控制实验系统。其中DSP作为主控芯片，功率板采用专用IGBT(Insulated Gate Bipolar Translator)驱动芯片和25 A、1 200 V的IGBT管。用霍尔传感器检测输出电流波形，使低压侧和高压侧完全隔离。直流侧电压采样，通过线性光耦隔离。6路PWM(Pulse-Width Modulation)控制信号输入，采用高速光耦完全隔离高压与低压侧的PWM驱动信号，保证驱动板不受高压干扰。利用磁粉制动器模拟负载转矩环境。硬件实验装置如图8所示。

图8 电机实验平台

实验控制参数为：PI控制器Kp=35，Ki=500；电流控制器Kp=100，Ki=200。扰动观测器实验参数为：cω=300，L=0.04。感应电机参数如表1所示。

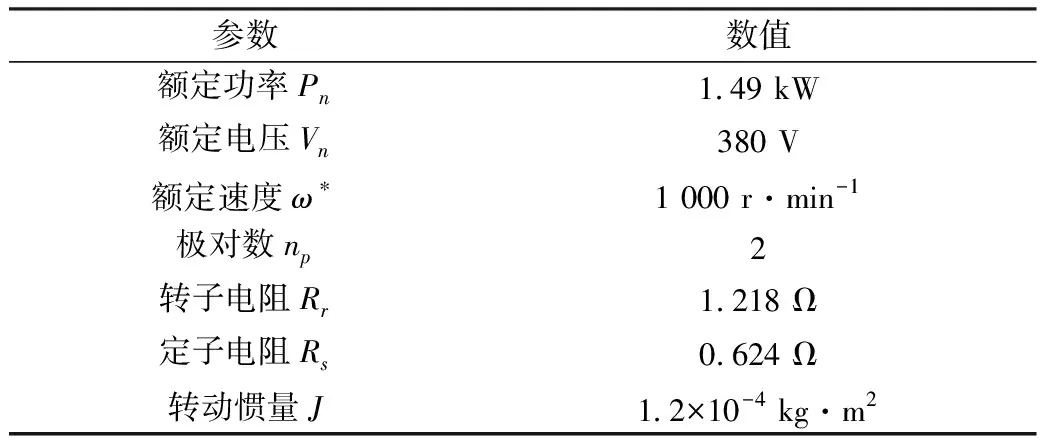
表1 IM电机参数

4.2 实验波形

电机在1 000 r·min-1下，外部负载为6 N·m时，在0.5 s突加和0.7 s突减时的实验波形如图9和图10所示。

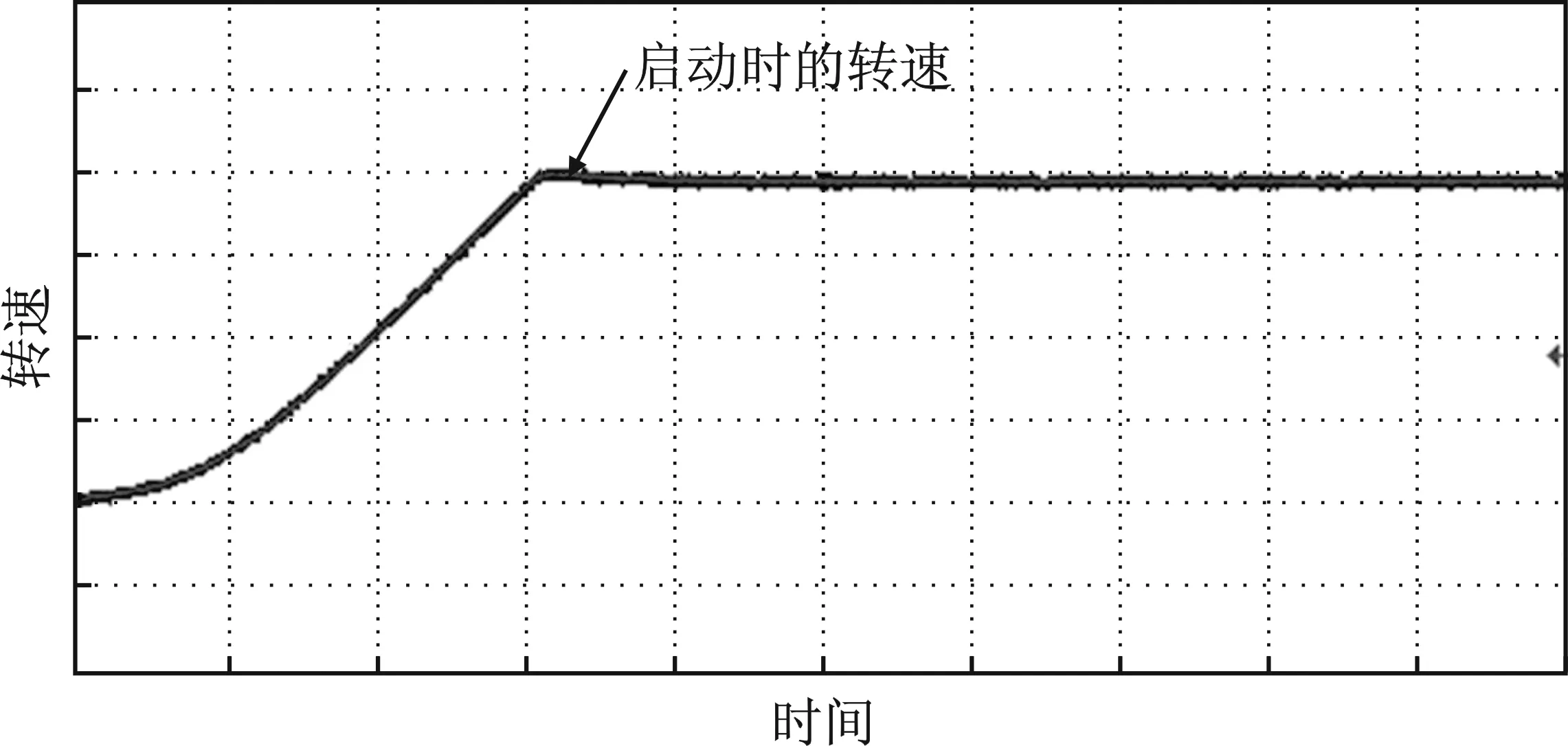
(a)

由图9和图10可知，本文所提出的改进扰动观测器研究算法在加减载时调节速度更快、波动更小，具体性能比较如表2所示。

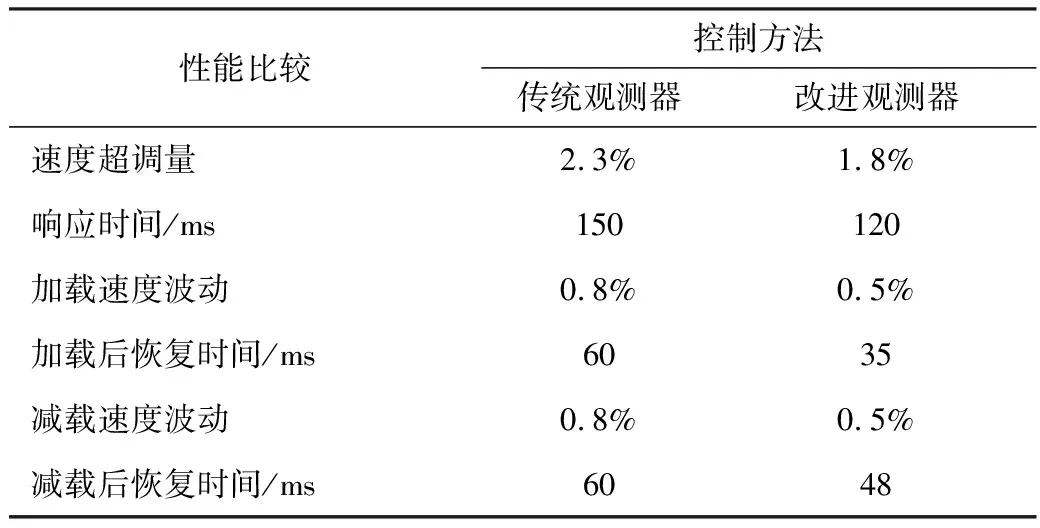
表2 3种控制算法的性能比较

5 结束语

针对于感应电机伺服系统，为了提高控制系统的负载转矩抑制能力，本文提出了一种基于新型扰动观测器的控制器。尽管通过良好的PI控制器在一定程度上可以提高速度环的控制性能，但当外部负载扰动突变过大时，PI控制器仍无法达到良好的抑制效果。在此基础上，采用传统滑模控制设计的扰动观测器可以观测到扰动并补偿到速度环，但该方法抖振过大，转速恢复慢。为此，本文设计了改进型扰动观测器，有效消除了抖振，平滑地估算了负载转矩，并将估算出来的负载转矩用作控制器的前馈补偿，提高了感应电机转速控制性能。在此研究的基础上，下一步计划从根本上解决PI控制器的局限性，设计出基于模型预测控制的算法，通过最优化算法思想来解决感应电机转速环在扰动下的问题。