基于支持向量机的轨道结构病害识别研究

伍伟嘉，杨 俭，袁天辰，邵志慧

(上海工程技术大学 城市轨道交通学院,上海 201620)

我国高速铁路运营里程的增长速度逐年增加，由高速、重载引起的轨枕空吊等病害严重影响列车的运行安全，该问题已引起了研究人员的广泛关注。现有的轨道结构病害检测手段主要有：超声波回弹法、地质雷达法、探测仪检测钢筋混泥土法、瞬变电磁法[1]等。这些方法主要依赖人工操作，检测效率低且无法实现在线检测。因此，建立高效的检测轨道结构病害的方法对于保障列车安全平稳运行具有重要的意义。

近年来，国内外学者在机械结构和大型土木工程结构故障模式识别方面做了大量研究。文献[2]建立了基于模糊C均值聚类算法的风电机组齿轮箱故障预警模型，有效解决了多组振动信号导致的报警结果不一致的问题。但是在样本数量有限的条件下，这种基于模糊聚类的模式识别方法的分类精度较低。针对这一问题，研究者利用神经网络算法[3-4]进行模式识别。文献[5]以桥梁结构模态分析所得的前4个固有频率为输入，基于人工神经网络和分类回归树，建立了桥梁伤损预测模型，克服了现有基于视觉检查的伤损检测方法的局限性。但该方法在面对小样本和高纬度数据时容易陷入局部最优，从而影响模式识别精度。针对这一问题，研究人员又开发了基于支持向量机(Support Vector Machine，SVM)算法[6-8]的模式识别方法。该方法具有很强的泛化能力，可以有效地处理小样本和高纬度数据。因此，本文采用支持向量机算法对轨道结构病害进行模式识别。

本文基于支持向量机算法实现了对轨道结构故障的识别。本文首先采用时域统计和离散小波变换对轨道结构病害下的轨枕振动加速度数据进行特征提取；然后提取香农特征熵并做归一化处理，剔除了无关信息使提取到的特征容易被支持向量机算法所利用；将提取到的特征向量集分为训练集和测试集，通过支持向量机算法对训练集进行学习并对测试集进行预测分类；最后，利用网格搜索方法优化支持向量机参数，实现了对轨道结构病害的准确识别。

1 车轨耦合动力学模型与工况仿真

1.1 仿真计算

本文采用文献[9]所提出的车辆-轨道耦合动力学模型，其结构如图1所示，其中车辆采用四轴二系悬挂的客车模型。在轨道模型中，轨下基础以各轨枕支点为单元沿纵向进行离散化处理，其中每个支承单元为双质量、三层弹簧-阻尼模型。本文根据道床锥体受荷假设把道床模拟为锥体。当模型中轨道的计算长度大于100 m时，轨枕的振动加速度几乎不受影响，故本文模型中的轨道长度l取120 m，轨枕间距ls取0.6 m。文献[9]中指出，轨枕空吊、道床板结、扣件失效等轨下基础缺陷属于动力型轨道刚度不平顺，若要对其进行模拟，只需改变模型中所对应的刚度和阻尼即可，例如轨枕完全空吊即完全失去工作能力，可以设Kbi=Cbi=0；对于道床板结，设置K′bi=ηkKbi以及C′bi=ηcCbi，其中ηk和ηc分别表示道床的刚度和阻尼变化系数。对于不同程度的病害，ηk和ηc可以在1～10之间取值。

图1 车辆-轨道垂向耦合模型

1.2 工况设置与仿真

在本文的工况仿真计算中，设置车辆行驶速度为200 km·h-1。选取轨道结构中心的第51～150共100根轨枕进行研究，并对不同程度轨枕空吊和道床板结工况下的轨枕振动进行了仿真。仿真方案见表1，图2为轨道结构不同病害程度的对比。

表1 轨道结构在不同工况条件下的模拟

从图2可以看出，不同程度轨枕空吊下的轨枕振动加速度的幅值有较大的变化，而不同程度道床板结下的轨枕振动加速度的数据差异并不明显。如果直接将未经处理的轨枕振动加速度数据进行分类识别，会因为数据特征不明显和冗余影响分类效果，因此需要对振动信号进行特征提取。

(a)

2 振动信号的特征提取

2.1 振动信号的时域统计分析

对于一个振动信号(A={Ai}，i=1～N，N为采样点数)来说，常用的时域特征有16个，可分为有量纲特征和无量纲特征。有量纲特征包括：最大值、最小值、均值、绝对均值、峰峰值、峰值、标准差、方差、方根幅值和均方根值。无量纲特征包括：偏度、峭度、波形因子、峰值因子、裕度因子和脉冲因子[10]。有量纲的特征值往往有具体的物理意义，是最为常用的时域特征指标，但其数值大小会受其他物理量的影响。

2.1.1 有量纲特征

(1)最大值Amax与最小值Amin。通过获取振动信号数据中数值最大和最小的值可以了解信号的振动幅值范围，计算式如下所示；

Amax=max(Ai)

(1)

Amin=min(Ai)

(2)

(2)均值Amean与绝对均值Aave。均值是指振动信号幅值的算数平均，也被称为信号的一阶矩。绝对均值是指振动信号幅值的绝对值的算数平均。

(3)

(4)

均值和绝对均值都可以用于描述振动信号的稳定分量，它们的值反映了振动信号波动能量的大小；

(3)峰值Ap与峰峰值App。峰值是指振动信号波形的最大瞬时值，如下所示。

Ap=|max(Ai)|

(5)

峰峰值指的是在一个周期内信号的最大值与最小值之间的差值，它反映了振动信号振幅的变化范围，计算式如下；

App=max(Ai)-min(Ai)

(6)

(4)标准差Astd与方差Avar。标准差是指振动数据中的各个元素与这组数据的平均数之差的算数平方和的平均数；方差则是标准差的平方。两者都可以描述振动信号的波动程度，是一种反应振动信号能量动态分量的特征参数。方差也被称为振动信号的二阶中心矩；

(7)

(8)

(5)均方根值Arms与方根幅值Ar。均方根值又叫有效值，它是描述振动信号强度的重要指标。振动信号的均方根值和方根幅值既可以反应信号的振动平均值，又可以反应振动信号的波动和离散度。

(9)

(10)

2.1.2 无量纲特征

(1)峭度Akurt与偏度Askew。峭度是振动信号四阶中心矩与标准差的4次方的比值。偏度又叫偏斜度或者偏态，它是振动信号三阶中心矩与标准差的3次方的比值。

(11)

(12)

峭度和偏度都是描述振动信号分布特性的特征参数。峭度反应了振动信号波形的平缓程度，对振动信号中的冲击成分比较敏感。偏度描述的是振动信号的非对称性；

(2)波形因子Asf、峰值因子Acf、脉冲因子Aif、裕度因子Aclf。波形因子被定义成均方根值与平均值的绝对值之间的比值，物理意义为实际振动波形与标准正弦振动波形的畸变和差异。

(13)

峰值因子指的是振动信号峰值与均方根值的比值，它描述的是振动信号峰值在波形中的极端程度，常用于检测振动信号中是否有冲击。但是由于振动信号峰值在不同时刻的变动较大，所以检测稳定性效果不佳。

(14)

脉冲因子是振动信号峰值与绝对均值之间的比值。与峰值因子一样，脉冲因子也可以用于振动冲击的检测。

(15)

从脉冲因子和峰值因子的定义可以看出它们比较相似，对于同一振动信号来说绝对均值总小于均方根值，故振动信号的脉冲因子大于峰值因子。

裕度因子是指峰值与方根幅值之间的比值。

(16)

2.2 振动信号的离散小波变换

小波变换以其多尺度特性在信号处理、图像分析和故障诊断等领域得到大量运用。离散小波变换(Discrete Wavelet Transform，DWT)作为小波变换的重要分支被广泛用于特征提取。与傅立叶变换(Fourier Transform，FT)有连续傅立叶变换[11]和离散傅里叶变换[12](Discrete Fourier Transform，DFT)类似，连续小波变换[13-15](Continuous Wavelet Transform，CWT)也有其对应的离散小波变换[16-17]。离散小波变换实际上是对连续小波变换的尺度和位移按照2的幂次离散化得到的。DWT的具体定义为

(17)

式中，x(·)是母小波；y(n)为初始信号；a0和b0为缩放和平移参数；通过改变m和n实现1,1/a,1/a2,…的几何缩放和0,n,2n,…的平移。通过数学变换可以把式(17)化为关于m和n的计算式，即

(18)

通过观察可以发现式(18)与有限脉冲响应(Finite Impulse Response，FIR)数字滤波器[18]的卷积方程有很大的相似性

(19)

其中，g(n-k)为FIR滤波器的脉冲响应。通过对比可知DWT的滤波器的脉冲响应方程为

(20)

令a0=1/2，b0=1，则a0m=1,1/2,…,1/2m，这样就可以使用以母小波作为低通滤波器的多级滤波器l(n)及其对偶滤波器h(n)来实现把信号分解为低频信号和高频信号的目的。

3 基于支持向量机的病害特征识别

3.1 支持向量机算法

支持向量机是一种主要用于解决二分类问题的算法。它的核心思想是以训练集为研究对象，在样本空间中找到一个超平面使得两类数据的边缘点与该超平面的距离尽可能远，如图3所示。

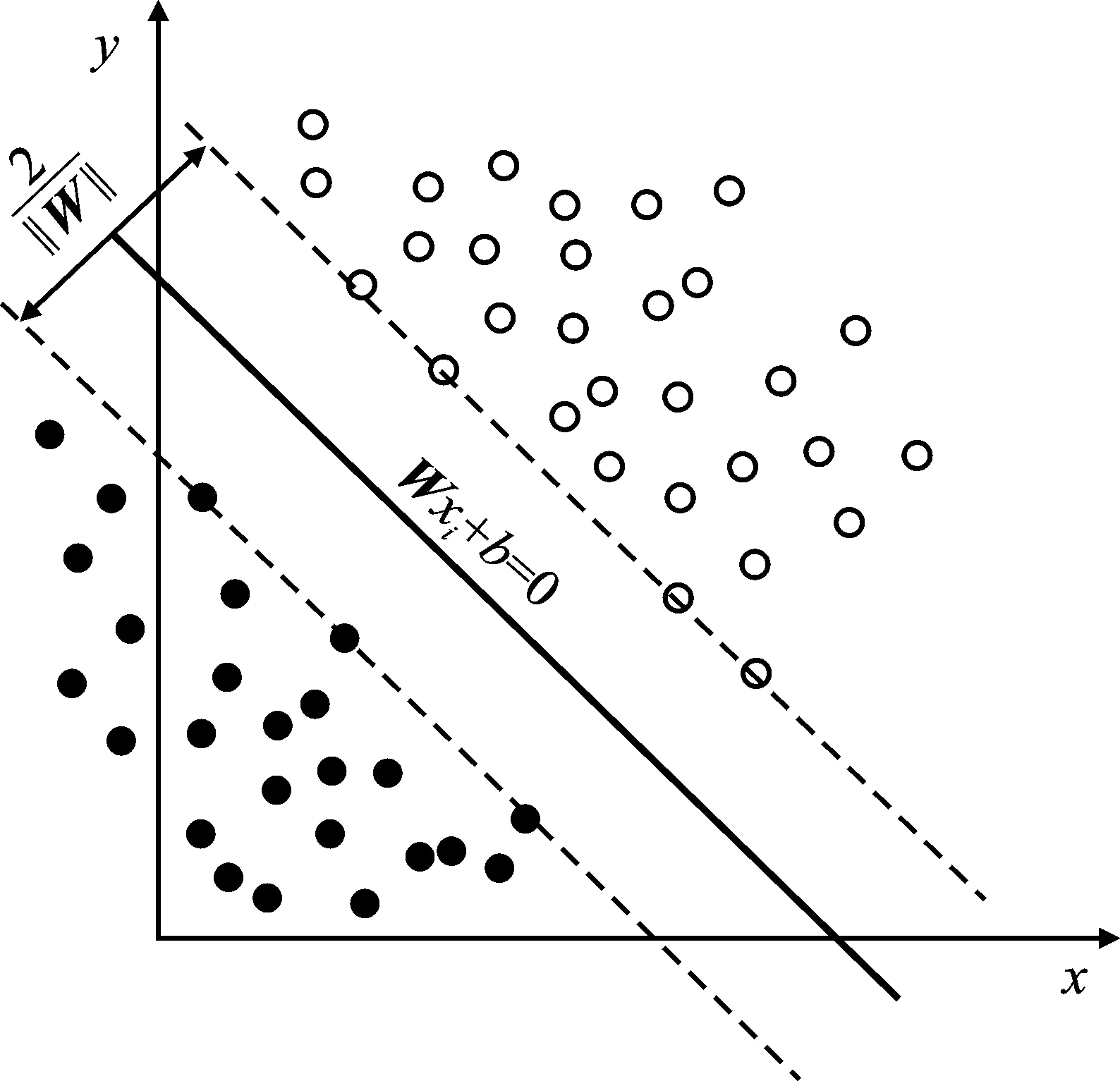
图3 支持向量机原理图

对于线性可分的情况，给定训练样本集A:(xi,yi)，1≤i≤N，xi∈Rd，y∈{-1,1}，其中N为样本长度，d为数据的维度。那么针对样本A的超平面可以定义为

Wxi+b=0

(21)

式中，W为超平面的法向量；b为超平面的“截距”。

对于样本空间中任意的样本点x，都可以用W和b表示为

(22)

为了让超平面可以使样本空间中所有数据尽可能实现分类，W和b需要满足如下约束

(23)

此时分类间隔即两类样本与超平面最近距离之和等于2/‖W‖，因此求解最优化超平面的问题就可以转化为一个凸优化问题，即

(24)

为了便于求解可将上述最大值问题转化为最小值问题，即

(25)

可以看出式(25)是一个凸二次规划问题，此类问题可以构造Lagrange函数进行求解。

(26)

将上式分别对W、b、k求偏导数并令其等于0，整理后代入式(26)中即可将求解最优超平面的凸二次规划问题转化为下式

(27)

假设k′=(k′1,k2′,…,k′N)≥0为最优解，则最优化超平面的函数可以表示为式(28)。

(28)

对于线性不可分的情况，可以通过核函数将样本变换到高维空间，转化为在高维空间上的线性问题。核函数的思想就是直接计算向量在特征空间Z中的内积，即找到一个函数k(x,y)使得k(x,y)=φ(x)φ(y)，其中φ(·)为映射函数。这样在不需要知道φ(·)具体形式的情况下就可以实现由线性不可分向线性可分的转换。根据Hilbert-Schmidt[19]理论可知，任何对称函数k(x,y)只需满足Mercer条件就可以作为核函数使用，于是线性不可分情况下的最优化超平面问题可以变为式(29)。

(29)

核函数的选择在很大程度上会影响SVM算法的分类准确率，SVM最常用的核函数为：

(1)多项式核函数

K(x,y)=(xTy+1)d

(30)

(2)Sigmoid核函数

K(x,y)=tanh(xTy+c)

(31)

(3)径向基函数

K(x,y)=esp(-‖x-y‖2/δ2)

(32)

其中多项式核函数属于全局性核函数，当数据维度较高时，SVM识别准确率会大幅下降。径向基函数对样本的维度和大小都没有要求，且学习能力强。通过选取合理的参数(惩罚因子C和核函数参数δ)即可实现对任意数据的准确分类，因此本文选取的SVM的核函数为径向基函数。

3.2 基于网格搜索的参数选择

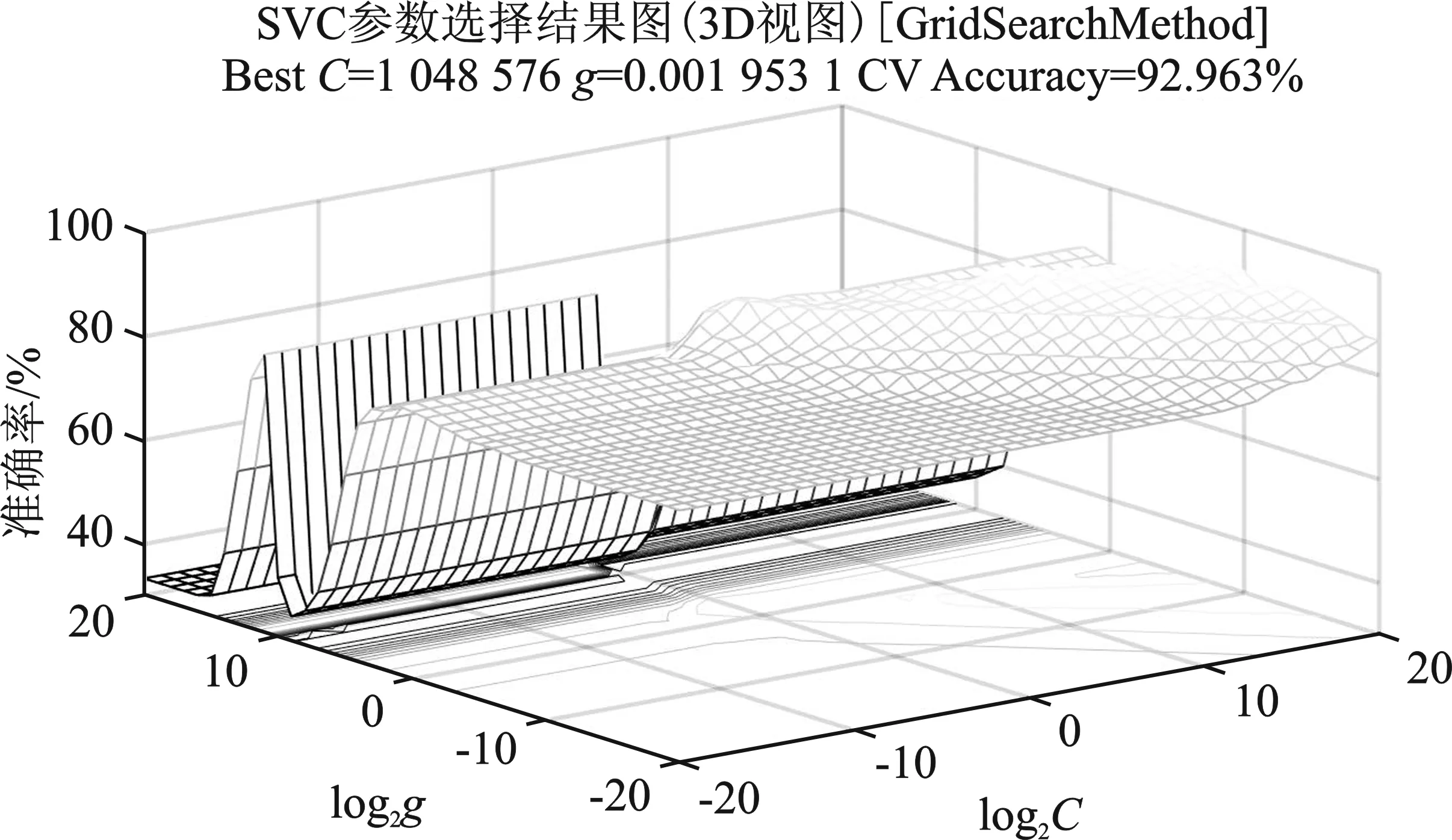
支持向量机的分类识别性能主要由惩罚因子C和核函数参数δ决定。用于确定上述两个参数的方法有粒子群算法、遗传算法、蚁群算法等，但这些算法往往容易陷入局部最优解的情况。本文选择网格搜索法对SVM模型参数进行最优化选择。

网格搜索算法的原理是将待优化的SVM参数C和δ的可行区间按设定好的步长划分为若干个小区间。对于确定的C和δ，将训练集输入到支持向量机中，利用交叉验证的思想计算分类准确率，最终选取分类准确率最高的C和δ作为最优参数。交叉验证是将训练集分成k组，并将其中的k-1组子集作为训练集，然后用训练出的支持向量机模型去测试剩下的那个子集，取k次测试的分类准确率的平均值作为此组参数C和δ对应的准确率。这种估值方法可以有效避免出现过拟合或者欠拟合的发生，基于网格搜索的支持向量机算法的具体流程如图4所示。

图4 支持向量机算法流程图

3.3 基于SVM的轨道结构病害识别

把章节1.2中仿真得到的不同工况条件下的轨枕振动加速度数据分成训练集和测试集，其中训练集90组、测试集10组。随后，对它们进行时频域联合特征提取(时域统计、离散小波变换)，其中离散小波变换选取db7作为母小波，分解层数为4层。将信号在一定尺度下进行分解，然后提取他们的香农特征熵并做归一化处理。将训练集输入到支持向量机中进行训练，并利用网格搜索算法对支持向量机的参数进行选优。利用训练得到的支持向量机模型对测试集进行分类识别，所得到的结果如图5所示，所对应的识别准确率分别为86.67%、90%和84%。

(a)

从图5(b)和图5(d)可以看出，该算法对于不同程度轨枕空吊或者道床板结的识别效果比较明显。从图5(f)可以看出把不同类型的故障放在一起进行识别时，算法的准确率较差。

4 结束语

本文利用时频分析方法提取了不同轨道结构病害下的振动特征，并在此基础上利用支持向量机算法进行模式识别，并对支持向量机的参数进行了优化。仿真结果验证了该方法对轨道结构病害识别的有效性。具体内容包括以下方面：(1)利用车轨耦合动力学模型对不同轨道结构病害进行建模，仿真得到了车速为200 km·h-1的正常状态、轨枕空吊以及道床板结条件下的轨枕振动加速度，并对比了不同程度轨枕空吊及道床板结下轨枕振动加速度的变化趋势；(2)利用振动信号的时域分析和离散小波变换提取了轨道结构病害的特征，建立了轨道结构病害特征矩阵，解决了轨枕振动数据维数高、信息较冗余的问题，为轨道结构病害识别奠定了基础；(3)将轨道结构病害特征矩阵分为训练集和测试集作为支持向量机算法的输入，并利用网格搜索算法对支持向量机算法关键参数进行选优。结果表明，对于不同道床板结病害，识别准确率为86.67%；对于轨枕空吊病害，识别准确率为90%；对于不同类型病害混合的情况，识别准确率为84%。本文所提出的基于支持向量机的轨道结构病害识别方法，实现了对不同程度轨道结构病害的识别，为轨道结构病害智能诊断提供了一种可行方案。