基于排列熵和支持向量机的轨枕病害诊断

邵志慧，杨 俭，袁天辰，伍伟嘉

(上海工程技术大学 城市轨道交通学院,上海 201620)

近年来我国高铁建设发展迅速，高铁运营里程稳居世界第一。截至2019年底，我国高铁运营里程突破35 000 km，占全球高铁里程的70%[1]。随着高铁线路长期运营，在列车动载荷、环境温度和其内部应力等因素的作用下，作为列车承载系统的轨道结构的各种病害日益凸显。有砟轨道的病害主要体现在轨枕空吊、道床板结、翻浆冒泥等。目前，国内外针对轨道病害的检测主要依靠轨检车和人工定期检测，此方式劳动强度大，效率低，漏检率高[2]。一旦无法及时发现轨道的病害，就有可能导致列车脱轨倾覆等灾难性的后果，因此对轨道结构的病害进行实时监测、病害判断和失效预警具有一定的现实意义。

由于轨道结构并非完全刚性，当轨道系统的某一部件出现病害时，整个轨道结构的动力学特性将会发生改变。因此，从轨道结构的振动响应中提取出病害信息是诊断轨道病害的关键。在对道岔设备的病害诊断和分类上，利用主题模型算法来提取病害的主题特征，并通过支持向量机算法，实现了道岔设备的病害诊断和分类[3]。为了有效诊断出基体裂纹等结构病害，文献[4]提出一种基于频率的声发射测量损伤诊断分类的方法。该方法使用短时傅立叶变换从测量信号中提取时频域特征，并利用支持向量机进行了诊断分类。针对大样本问题，文献[5]提出一种综合压缩感知和变分模态分解方法(Variational Mode Decomposition，VMD)有效地识别了船舶推进轴系轴承的故障特征。为了解决数据特征高维、冗余等问题，文献[6]基于可分度函数与支持向量机算法，降低了故障特征的冗余程度，提高了分类效率和精度。此外，文献[7]利用主成分分析法和K-means聚类算法对监测数据进行了病害特征提取，实现了对混凝土结构不同病害的诊断。文献[8]提出了一种基于递归神经网络(Recursive Neural Network，RNN)和长短期记忆神经网络(Long Short Term Mermory Network，LSTM)融合的磨矿系统故障智能诊断方法。研究人员通过LSTM神经网络提取出样本与时间的相关性，再利用RNN神经网络对比故障前后时刻输入特征的变化实现故障诊断，将故障诊断的错误率降至3%。针对钢轨表面缺陷识别的问题，文献[9]提出了一种基于Faster R-CNN(Radon-Convolutional Neural Networks)的检测方法，并实现了对4种钢轨表面缺陷的分类识别，识别精度均达到了90%以上。一些大型设备焊接部位的可靠性在工业生产中起着举足轻重的作用。文献[10]基于主成分分析(Principal Component Analysis，PCA)和支持向量机(Support Vector Machine，SVM)实现了对焊缝缺陷信号的分类识别，为焊缝缺陷检测提供了有效的方法。然而，针对轨道结构病害诊断方法的研究仍处于起步阶段。

近年来，排列熵作为一种描述时间序列复杂程度的度量，正逐渐从医学、生物和气候[11-13]等方面向机械病害诊断领域扩展。排列熵的概念于2002年提出[14]，该方法针对时间序列动态变化的检测具有计算效率高、鲁棒性强、结果直观等优点。因此，本文以有砟轨道的轨枕为研究对象，通过研究轨枕病害时的动力学表现，提取轨枕振动响应时间序列的排列熵值(其在归一化处理后能够清晰地反应轨枕病害的变化)，并基于此构建了轨枕病害诊断的特征集，从而降低了数据的维度，减少了后续算法的运行时间。本文以排列熵值特征集为输入，基于遗传算法优化的支持向量机对轨枕病害进行分类，实现了对轨枕4种病害服役状态的诊断，从而为轨道结构病害的智能诊断方法研究提供一定的依据。

1 轨枕病害模拟仿真

对于车轨耦合动力学模型，本文基于文献[15]，采用四轴二系悬挂整车模型，将轨道系统模拟成3层弹簧-阻尼连续弹性支承的轨道模型。其中，钢轨采用连续弹性离散点支承Euler梁，将轨下基础(道床-路基)沿纵向离散，并以各轨枕之间的间距将离散点间隔开，图1给出了车轨耦合垂向振动模型。基于文献[15]，本文建立的车轨耦合模型中，选取轨道长度l为120 m，各轨枕之间的间距ls为0.6 m。针对轨下基础结构的模拟，文献[15]中给出了相应的解决方法，即通过对弹簧和阻尼器逐一进行赋值，便可模拟出轨道系统结构存在的病害。本文的研究对象是轨枕病害，当道床形成了局部暗坑时，轨枕会出现空吊病害。若某一轨枕与道床之间的空隙过大以至于该处的道床完全失去支承能力，则可在模型中设置该处道床的刚度和阻尼为0；若某一轨枕与道床之间的间隙并不大，该处道床还可发挥其部分支承能力，则可以通过分别改变道床的刚度和阻尼系数来模拟轨枕不同的病害。

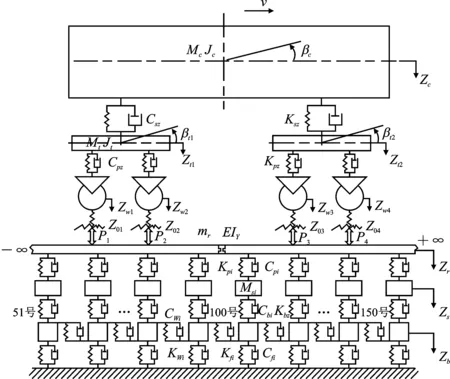
图1 车辆-轨道垂向耦合振动模型

基于上文所建立的车辆-轨道耦合振动模型和本文的研究对象，则第i号轨枕的振动方程为

(1)

式中，Msi为单位长度轨枕的质量；Zsi为轨枕的振动位移；Cpi和Kpi分别为轨下垫层的阻尼和刚度；Cbi和Kbi分别为道床的阻尼和刚度。

对轨枕振动响应仿真数据描述如表1所示。选取第51～150号轨枕作为仿真对象，分别以5种轨道不平顺谱作为激励，仿真出列车的速度分别为100 km·h-1、110 km·h-1、120 km·h-1、130 km·h-1、140 km·h-1、150 km·h-1、160 km·h-1、180 km·h-1和200 km·h-1的轨枕振动加速度。设置轨下道床的4种刚度和阻尼，分别为：K′bi=Kbi、C′bi=Cbi(S1)；K′bi=0.9Kbi、C′bi=0.9Cbi(S2)；K′bi=0.7Kbi、C′bi=0.7Cbi(S3)；K′bi=0.5Kbi、C′bi=0.5Cbi(S4)，并对这4种服役状态进行仿真。

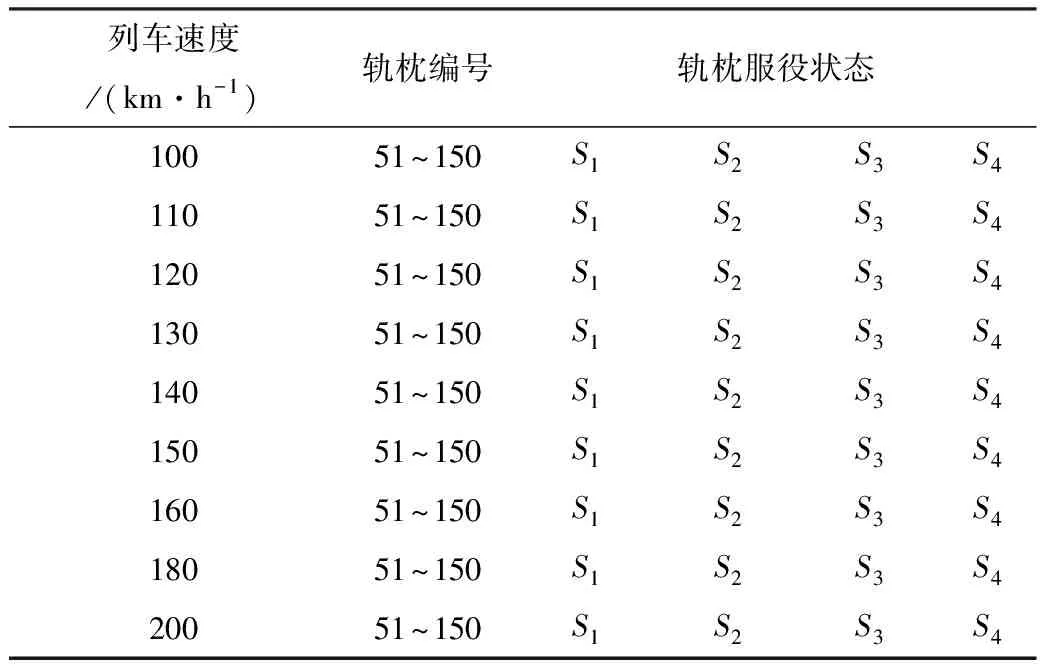
表1 各轨道不平顺谱下的轨枕振动响应仿真数据

根据表1对轨枕振动响应进行仿真，设定采样频率为10 kHz，采样点数由车辆走完模型中的轨道全程的速度和所需的时间决定。

2 轨枕振动信号排列熵特征提取

2.1 排列熵原理

轨枕发生病害后，其支撑层的刚度和阻尼发生变化，进而导致轨枕振动响应的复杂度也相应产生变化，因此通过排列熵来描述振动信号的复杂度可以较好地反应轨枕的服役状态。排列熵算法[16]通过嵌入维数m和延迟时间τ将时间序列在相空间上进行重构，得到k个重构分量。再将k个重构分量按照递增的方式重新排列，最终将时间序列转化为符号序列，并通过统计符号序列的概率分布来计算时间序列的复杂度。排列熵算法的具体步骤如下：

步骤1对时间序列{X(i),i=1,2,…,n}进行相空间重构，得到如下矩阵

j=1,2,…,k

(2)

式中，m为嵌入维数；τ为延迟时间；k=n-(m-1)τ。将相空间矩阵的行向量看作重构分量，则共有k个重构分量；

步骤2将X(i)相空间重构矩阵中第j个分量(x(j),x(j+τ),…,x[j+(m-1)τ])按照数值递增排列，j1,j2,…,jm为重构分量，如式(3)所示。

x[i+(j1-1)τ]≤x[i+(j2-1)τ]≤…

≤x[i+(jm-1)τ]

(3)

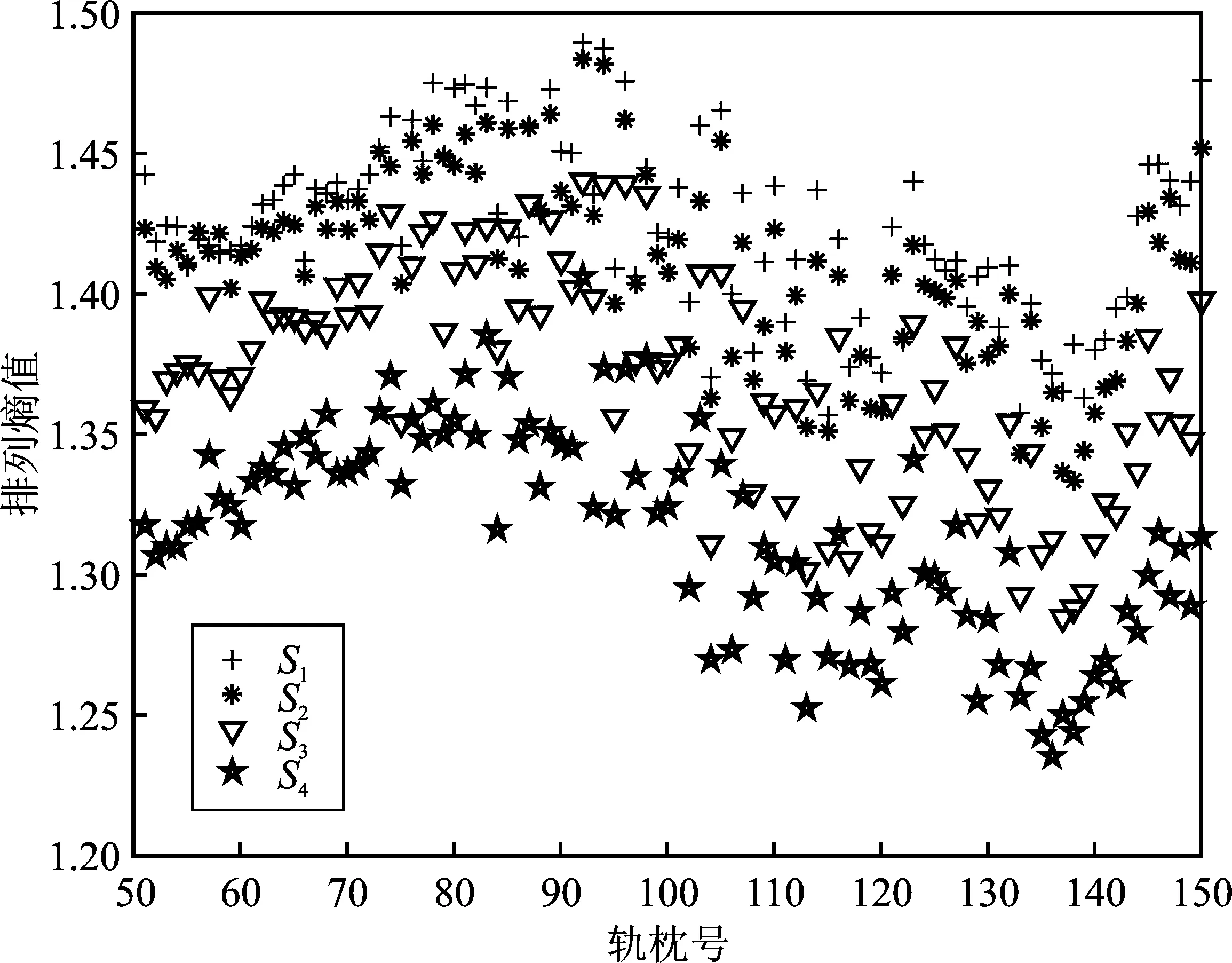
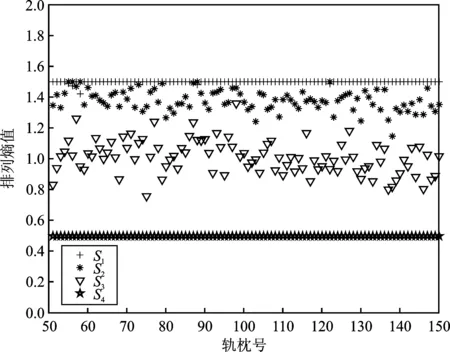
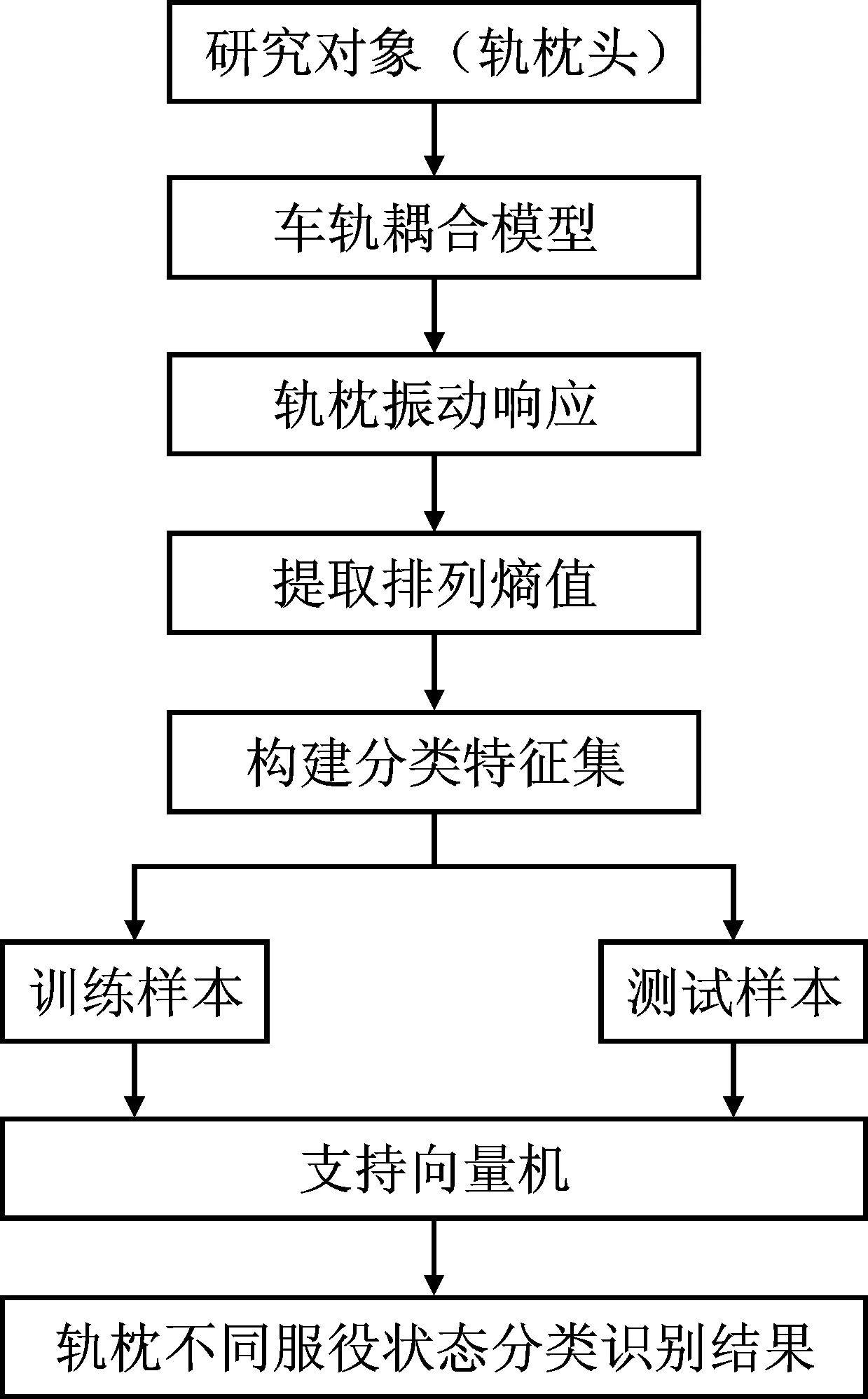
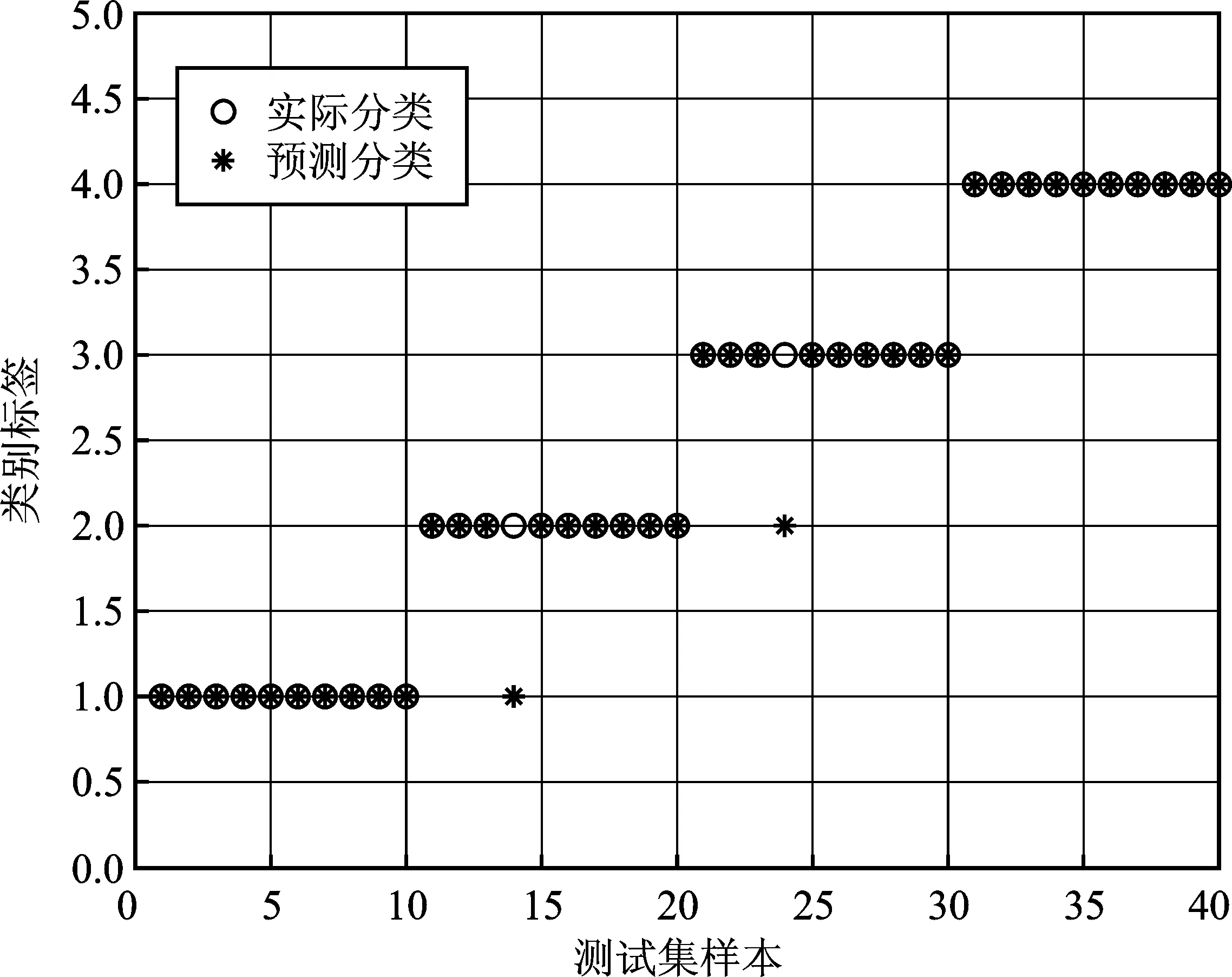
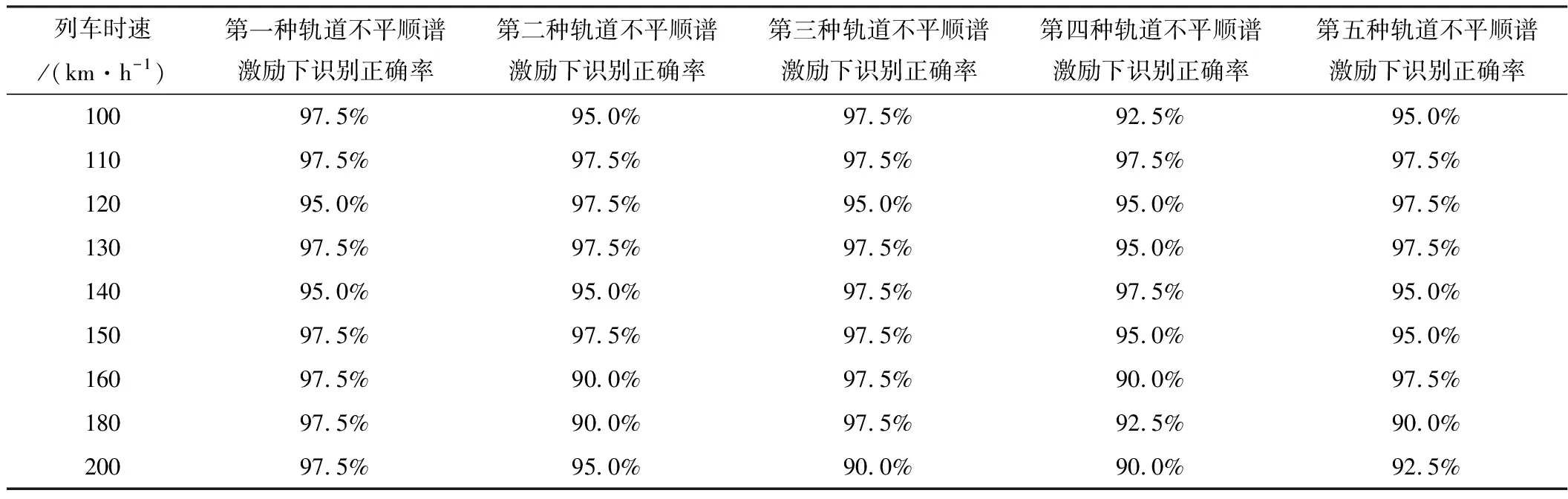
若重构分量中x[i+(j1-1)τ]=x[i+(j2-1)τ]，那么它们的排序根据j1和j2的大小来判断，也就是说当j1

x[i+(j1-1)τ]≤x[i+(j2-1)τ]

(4)

步骤3任意一个时间序列X(i)的重构矩阵的每一行均可以得到一组符号序列

S(l)=(j1,j2,…,jm)

(5)

式中，l=1,2,…,w，且w≤m!，即m维相空间总共有全排列m！个符号序列；

步骤4计算符号序列在全排列中出现的概率P1,P2,…,Pn，有

(6)

步骤5根据香农熵的定义，时间序列X(i)的排列熵定义为

(7)

当Pj=1/m!时，Hp(m)=ln(m!)，此为Hp(m)的最大值。为了能更加直观地表示排列熵，通常对其进行归一化处理

0≤Hp(m)≤1

(8)

式中，Hp值反应了时间序列的复杂度，排列熵越小，时间序列越复杂；反之，时间序列越有序。

2.2 轨枕病害特征提取

提取振动响应的特征信息主要是希望通过分类器来实现数据集的诊断分类。尽管不同类型的分类器对数据集的分类效果有所差别，但在大多数情况下，分类正确率的高低取决于特征的提取。若能够从轨枕的振动响应中提取到理想的特征信息，那么就能够减轻分类器的分类任务[17]。因此特征提取是诊断轨枕病害的关键步骤之一。

从上文仿真得出的轨枕振动加速度为原始数据，基于排列熵算法提取轨枕振动响应的病害特征需要选择合适的嵌入维数m和延迟时间τ。文献[14]给出的嵌入维数的最佳取值范围3≤m≤7，在本文中选取嵌入维数m=6。由于当数据长度大于512时，延迟时间τ对排列熵值的大小几乎没有影响[18]，故选取延迟时间τ=1。然后，通过排列熵算法计算每根轨枕在各个服役状态下的排列熵值。本文以轨道不平顺谱激励下的111～120号轨枕在列车速度为150 km·h-1时的排列熵为例，如表2所示。

表2 111～120号轨枕在列车速度为150 km·h-1时不同服役状态的排列熵值

由表2可以看出，在列车速度为150 km·h-1时，每根轨枕振动响应的排列熵值随着病害的增加而减少。虽然随着病害的增加，排列熵值变化并不明显，但在对排列熵值进行归一化处理后，其可以较理想地表现出轨枕的不同病害状态，即以排列熵值作为分类器的输入数据在理论上是可行的。时速为150 km·h-1时的原始排列熵值和归一化后的值如图2和图3所示。

图2 150 km·h-1时各轨枕的原始排列熵值

图3 150 km·h-1 时各轨枕排列熵归一化后的值

根据图2和图3的对比可以看出，在同一速度下，各轨枕不同服役状态的原始排列熵值虽然有细微的差别，但作为分类算法的输入数据会影响其分类诊断的性能。因此，利用归一化算法对同一轨枕的4种状态的排列熵值进行处理，可以增大数据间的相对差别，从而提高分类算法的诊断效率。

3 基于支持向量机算法的轨枕病害诊断

3.1 支持向量机的基本原理

支持向量机作为传统的分类器模型，其核心是找到一个能够准确地将样本分为两类的最优超平面。而当需要分类的数据线性不可分时，将样本向高维空间投影，可以实现在高维空间中对样本进行划分，解决样本线性不可分的问题。然而，当样本本身维度较高时，向高维空间投影很有可能会导致维度爆炸。为了解决这一问题，本文引入了核函数。目前国内外普遍采用的核函数是高斯径向基核函数(Radial Basis Function，RBF)，其表达式如下所示

(9)

式中，σ为高斯径向基核函数的宽度。

核函数作为影响支持向量机分类效果的关键因素，惩罚因子C和σ2是决定支持向量机分类性能的重要参数。为了能够获得更为精确的分类结果，本文选择遗传算法对惩罚因子C和σ2进行选择和优化：首先将惩罚因子C和σ2的参数形式转化为基因编码的表达形式，形成由200个个体组成的种群规模；然后从惩罚因子C和σ2的解空间中随机选择一个起点出发，利用适应度函数指导其搜索的方向；最终选取训练准确度最高的C和σ2作为最优参数，为了提高运算速度，本文选取进化代数为20。

3.2 基于支持向量机的轨枕病害诊断

结合排列熵算法和支持向量机，提出的轨枕病害诊断分类方法流程如图4所示。该方法步骤包括：

图4 轨枕病害诊断流程图

步骤1利用车轨耦合垂向振动模型，获取轨枕的振动响应；

步骤2利用排列熵算法，提取轨枕振动响应的排列熵值构成特征向量；

步骤3以提取的排列熵值特征向量作为支持向量机的输入，对其进行训练和测试，最终实现对轨枕病害的诊断分类。

根据图4所示的流程，本文对5种轨道不平顺谱下，不同列车速度时的4种轨枕服役状态进行分类识别。在同一个轨道不平顺谱下，每一个列车速度对应着100根轨枕的4种服役状态，分别为S1、S2、S3和S4。具体地，每一种服役状态有100组排列熵值，分别选取S1、S2、S3和S4这4种服役状态的前90个排列熵值作为训练集，剩余的10个排列熵值作为测试集，具体的数据描述如表3所示。

表3 各列车速度下的实验数据描述

根据上述方法，以第4种轨道不平顺谱作为激励，列车速度150 km·h-1时的100根轨枕振动响应为例，分别利用利用支持向量机对归一化前和归一化后的排列熵值进行训练和识别，得出的分类结果如图5和图6所示。

图5 归一化前的正确率

图6 归一化后的正确率

根据图5和图6可以看出，归一化后的识别正确率从52.5%提高到了95%，40个样本中仅有两个样本分类错误，说明识别正确率得到了显著改善。为了使基于排列熵和支持向量机的轨枕故障识别方法更具说服力，本文分别对5种轨道不平顺谱下，各列车速度时的4种轨枕服役状态进行了分类识别，识别结果如表4所示。

表4 不同轨道不平顺谱下各列车时速对应的分类正确率

根据分类结果可以看出，基于支持向量机并以排列熵值作为轨枕病害诊断的特征输入，可以得到较为理想的分类结果。在选取的每一种轨道不平顺谱的激励下，不同列车速度下的轨枕病害分类精确度均能达到90%以上，甚至在某些速度下轨枕病害分类精确度能够达到97.5%，仅有一个测试样本诊断有误。以上结果证明了本文所提方法在轨枕病害诊断上的鲁棒性和有效性，表明本文所提出的轨枕病害诊断方法在工程具有良好的应用前景。

4 结束语

轨枕病害诊断方法的研究对实现轨道服役状态的诊断具有指导性意义。本文以轨枕病害为研究对象，提出了一种基于排列熵和支持向量机的轨枕病害诊断新方法，并得出如下结论：(1)利用排列熵算法提取了轨枕振动加速时间序列的排列熵值，并在对其归一化之后，发现其能够较好地反应轨枕下道床刚度和阻尼产生变化后轨枕振动响应复杂度的改变。本文构建了基于归一化后排列熵值的轨枕病害诊断的特征集，降低了数据的维度，也减少了后续算法的运行时间；(2)本文以归一化后排列熵值的轨枕病害诊断的特征集为输入，利用遗传算法优化的支持向量机对轨枕不同病害状态进行诊断分类。最终的诊断精确度均达到90%以上，且某些条件下的病害诊断精确度达到了97.5%，说明本文所提方法实现了对轨枕不同服役状态的诊断。