关于椭圆接触弹流润滑Hamrock-Dowson膜厚公式的再思考

金 微,郭 峰,荆兆刚

(青岛理工大学 机械与汽车工程学院,山东 青岛 266520)

椭圆接触弹流润滑广泛存在于机械零部件中，如各类滚动轴承和齿轮.在上世纪70年代，Hamrock和Dowson发表了关于椭圆接触等温弹流润滑的研究成果[1-3]，其中包括著名的Hamrock-Dowson膜厚公式(简称H-D公式).80年代，朱东和温诗铸[4]研究了椭圆度及乏油对润滑的影响.Chittenden和Dowson等[5-6]研究了卷吸速度与接触椭圆的长轴重合以及卷吸速度与接触椭圆的短轴成一定夹角的点接触问题.在此之后，国内外众多研究人员研究了卷吸速度[7-9]、热效应[10-13]和乏油[14-15]等对弹流润滑的影响.椭圆比是椭圆接触弹流润滑中的1个重要的几何参数，在工程实际中有重要意义，如发动机凸轮-挺杆和鼓形轴承滚子的润滑等.多数弹流文献研究的重点大都放在载荷、速度和材料参数对润滑状态的影响上，对椭圆比的研究相对较少，最具影响的是H-D公式关于点接触弹流的膜厚与椭圆比关系的表达及Chittenden等的后续工作.

在润滑工程设计中，最常用文献[2]中的H-D公式估算弹流润滑膜厚.文中结果表明无量纲载荷、速度和材料参数不变时，椭圆比大于6之后，中心膜厚不变.将H-D公式中无量纲载荷用接触区中心赫兹压力表示时，发现当维持接触区中心赫兹压力为常数，增加椭圆比ke超过一定值时，得到的中心膜厚不升反降，这不符合物理规律，引起H-D中心膜厚公式的预测误差会增大.本文作者应用有限单元法(FEM)，借助Comsol Multiphysics软件求解等温椭圆接触弹流问题.研究了椭圆比对中心膜厚的影响，并与H-D中心膜厚公式进行对比.构造出表征椭圆接触的综合几何参数，对H-D中心膜厚公式进行了修正，使得膜厚的计算更加合理.

1 椭圆接触弹流润滑控制方程

稳态等温椭圆接触弹流润滑模型如图1所示，固体1和2在接触区表面沿x方向的速度分别为u1和u2，卷吸速度为ue.令Rx≤ Ry，即令卷吸速度方向与接触椭圆短轴重合.

Fig.1 Geometrical description of elliptical contact EHL 图1 椭圆接触弹流润滑的几何描述

无量纲雷诺方程如下，

上述未列参数见符号表.

1.1 膜厚方程

膜厚方程有三部分组成，包括刚体位移H0，几何间隙G(X,Y)和接触面的弹性变形W(X,Y).

对椭圆形滚子，无量纲的几何间隙为

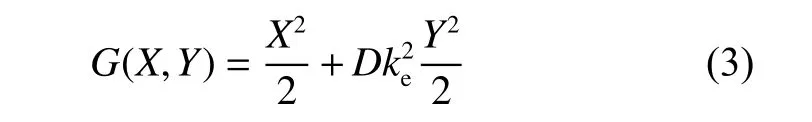
两固体间的弹性变形W(X,Y)应用三维弹性方程求解.为了简化模型，应用等效的弹性模型计算1个接触面的弹性变形代替两个接触面弹性变形的总和.这样，固体材料的特性可简化为

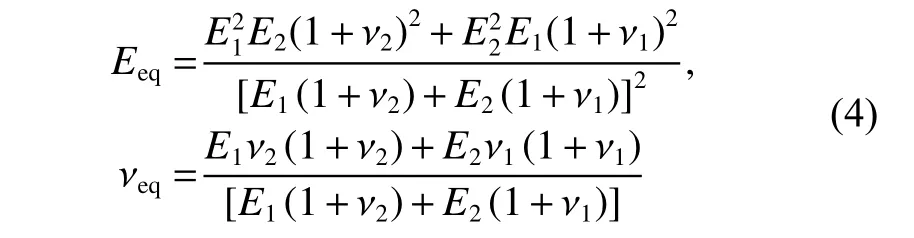
因此，三维弹性方程无量纲形式改写成式（5）.

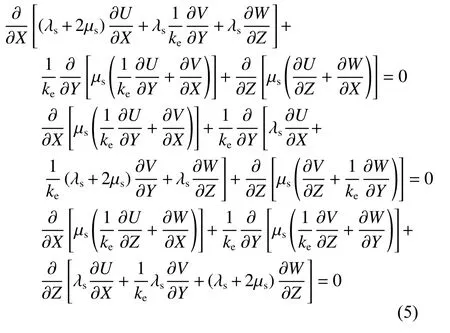
其中，λs和μs均为拉梅参数：

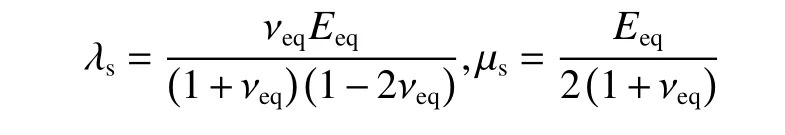
通过上述方程可求解出弹性变形W(X,Y)，更多公式推导细节可参考Habchi等[16].

确定方程合适的求解区域非常关键.椭圆接触弹流润滑问题具有对称性，因此选取半域计算，可减少计算量和缩短计算时间.如图2所示，计算域为 Ω，固体立方结构的尺寸至少要大于60倍的赫兹接触半径才能满足半无限空间求解的弹性形变；二维雷诺方程的计算域 Ωc,取-4.5≤X≤1.5和 -3≤Y≤3能够满足边界处压力为零；∂Ωs为对称面，在XZ平面内.

因此，上述方程需要满足的边界条件为

Fig.2 Computation domain of the elliptical contact EHL图2 EHL椭圆接触问题的计算域

1.2 载荷平衡方程

计算域内流体动压产生的压力总和用于平衡外载荷，考虑到对称性建立的半域模型，在接触区Ωc内压力积分为 π/3，而不是2π/3.

2 数值计算

同时求解雷诺方程(1)、膜厚方程(2)、线弹性方程(5)和力平衡方程式(6)，可得到接触区内压力分布和油膜外形.采用有限元方法求解这些非线性微分方程.在高载荷条件下，雷诺方程是不稳定的，会出现振荡.采用伽辽金最小二乘有限元法(GLS)和各向同性扩散技术对雷诺方程(4)进行了修正.因此，修正后的离散的稳态雷诺方程弱表达式为

其中：前两项是雷诺方程的伽辽金形式，第三项是惩罚项，使接触区内负压为零，第四项是GLS项，最后1项是ID项，两者用于消除伪震荡现象，并且无残差.Wp是压力的权函数， Ωce是计算域中Ωc单元的集合.方程式(7)中的参数表达式如下：

其中：ρID是各向同性扩散系数，he和Pe分别是特征长度和局部Pelect数.

2.1 全耦合模拟

采用通用的有限元软件进行有限元分析.把所有方程联立成非线性方程组，作为1个整体，将所有的因变量P、U、V、W和H0整理到1个未知向量中，线性化后用New-Raphson迭代法求解.流体动压部分采用拉格朗日五次插值函数，弹性形变部分采用拉格朗日二次插值函数.在接触区Ωc内，中心赫兹接触部分网格的最大尺寸不超过0.1，并在靠近出口区处加密，因为在弹流润滑时此处会出现二次压力峰.其他部分的网格尺寸最大尺寸不超过0.5.在整个接触域Ω内选择比较粗糙的网格就能满足计算要求.自由度大约为60 419，相对容差在10−3～10−4之间.使用Inter(R) Xeon(R) CPU E5-2630处理器，迭代4次，经过20 s即可收敛.如果选择合适的压力初值，能减少迭代步数，缩短计算时间，因此合理地选择压力初值尤为重要.

2.2 验证

本文作者应用有限单元法计算弹流润滑的压力分布和油膜厚度，与多重网格法(MG)的计算结果相互比较，如图3所示.计算参数为ke=1、α=2.19×10−8Pa−1、Rx=0.02 m、η0=0.08 Pa·s、UR=5.0×10−11、W=1.0×10−6和G=5 000.图中对比了Y=0处的压力分布和油膜厚度，两种方法的计算结果吻合，证明了本文方法的正确性.

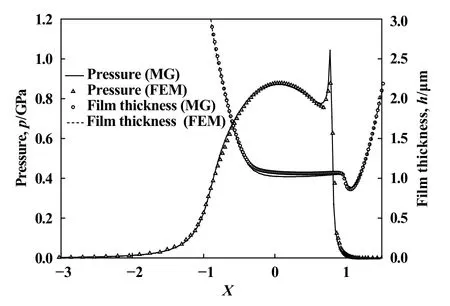
Fig.3 Comparison of results between finite element method with Multigrid method图3 有限单元法和多重网格法计算结果的比较

3 结果与讨论

3.1 载荷不变时中心膜厚随椭圆比的变化

图4所示ke= 2、4、6、10、15时，椭圆接触油膜厚度和压力分布等值云图.在油膜厚度等值云图中，椭圆比对马蹄形油膜的形成具有重要影响.随着椭圆比ke的增加，油膜的马蹄形特征越不明显，两个侧缘越来越小，之间的距离越来越远；油膜的平行部分缩短.在压力分布等值云图中，随着椭圆比ke的增加，二次压力峰先升高到最大值之后开始下降，并向接触区中心移动.这表明当外载荷一定时，增加ke，承载面积增加，润滑状态由弹流润滑变化到动压润滑.

Fig.4 Pressure and film thickness vs elliptic ratios under constant load (UR =5.0×10−11，W=1.0×10−6)图4 载荷不变时油膜厚度和压力随椭圆比的变化 (UR =5.0×10−11，W=1.0×10−6)

图5所示为本文数值计算和H-D公式得到的中心膜厚Hcen随椭圆比的变化.ke的取值范围从1(点接触)到16(中心接触区为线接触状态)，可以看出，两者趋势相差很大.在ke=1～8之间，H-D公式和数值计算表现出相似的变化趋势，Hcen随ke的变化表现为先快后慢，数值的差别应来自于计算方法和网格数的不同.ke>8以后，H-D公式中的Hcen基本不变；当UR=5.0×10−11，W=1.0×10−6时，在本文数值计算中，Hcen随ke的增加而逐渐下降.随椭圆比ke增加承载区域增加，当外载荷不变时，油膜压力水平降低，导致油膜厚度增加，润滑状态由弹流润滑转变到动压润滑，同时油膜压力的降低会使固体弹性变形变小，对油膜厚度的贡献降低，又会使得油膜降低.最终的油膜厚度是以上两种效应共同作用的结果.需要指出的是，Hamrock和Dowson在H-D中心膜厚公式回归过程中，使用的椭圆比最大为8.椭圆比ke= 8～16之间的油膜厚度公式没有数值计算点的约束，只是回归公式的外插值.

3.2 接触中心Hertz压力不变时中心膜厚随椭圆比的变化

为了进一步检验H-D公式中Hcen与ke的关系，保持接触区中心赫兹接触压力不变，就ke= 1～16时对应的Hcen值进行了计算，结果见图6，其中表示由H-D公式计算出的中心膜厚，表示有限单元法数值计算的结果.以ph=0.4 GPa，UR= 5.0×10−12为例，由图6可知，随着ke的增加，缓慢增加，在ke>10以后趋近于定值.在ke=1～5时随ke的增加而增加，而ke>5以后呈现下降的趋势，ke=16时的计算值(1.549)与ke=5时的计算值(1.654)相比，下降了6.3%，这与物理现象是相悖的.当接触中心压力不变时，随着ke增加，端泄对中心膜厚影响减小，中心膜厚不应出现减小的趋势.

定义几何参数θ

最大接触Hertz压力可改写为

Fig.5 Central film thickness vs ellipticity ratio under constant load by the method of H-D formula and FEM图5 由H-D公式(a)和FEM法(b)计算出恒定载荷时中心膜厚与椭圆比的关系

Fig.6 Central film thickness vs.ellipticity ratio under constant Hertz pressure calculated by H-D formula and FEM图6 由H-D公式(a)和FEM法(b)计算出恒定赫兹压力时中心膜厚与椭圆比的关系

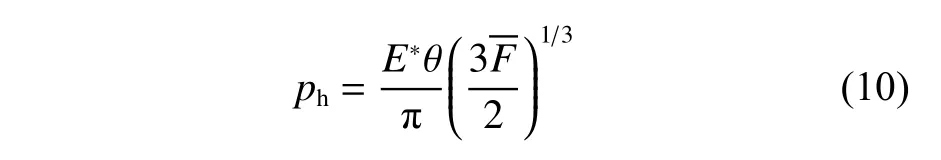
引用参数θ对H-D公式等效变换，θ仅与椭圆比有关，而与Rx、Ry无关.由式(10)得

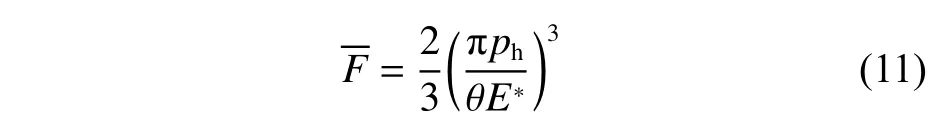
H-D中心膜厚公式:

因E′与E*相差2倍，所以H-D公式中的为

代入H-D中心膜厚公式(12)中，得

其中：esl称为中心膜厚端泄因子

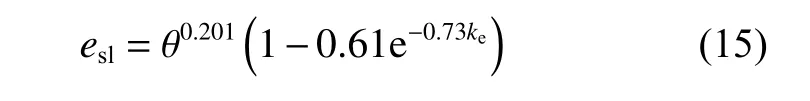
从理论上讲，esl应为ke的增函数，而实际上，由表达式(15)求出当ke≈4.6时，esl取得最大值.图7为按式(15)绘出的esl与ke的关系图.可以看出在ke≈4.6之后，esl为ke的减函数.因此，可经过大量的数值计算，构造出以θ为基本参数的端泄因子表达式，对现有的端泄因子进行修正.

Fig.7 Variation of leakage factor esl as a function of ellipticity ratio ke图7 端泄因子esl与椭圆比ke的关系

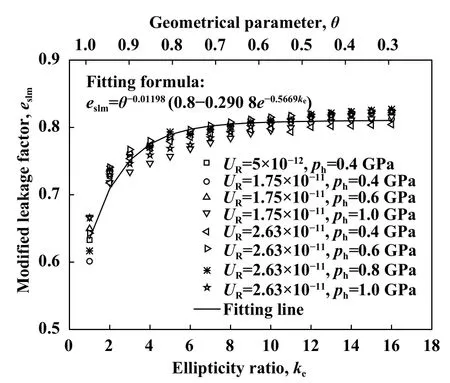
Fig.8 Variation of modified leakage factor eslm as a function of ellipticity ratio ke by numerical fitting图8 数值拟合出修正端泄因子eslm与椭圆比ke的关系曲线

图8分别给出了不同的载荷和速度时，根据数值计算得到的修正端泄因子eslm与ke的关系.其中散点是计算值，实线是拟合曲线.根据离散点拟合出如下修正的中心膜厚端泄因子:

同时在图8上方绘制出了与ke对应的θ值.可以看出，θ与esl成反比的关系.但是，由H-D中心膜厚公式推导出的端泄因子式(15)中，θ与esl是正比的关系.由此可见，修正后的端泄因子式(16)更加合理.

3.3 椭圆接触弹流润滑中心膜厚修正公式

根据以上数值分析的数据，得到以下椭圆接触弹流润滑中心膜厚的修正公式.

与经典的Hamrock-Dowson公式相比，式(17)的中心厚度对端泄因子进行了修正.对修正后的公式精度进行了检验，结果列于表1中.

由表1可见，通过上述修正公式得到结果与数值计算结果具有较好吻合性.

表1 中心膜厚数值计算结果及修正公式计算结果比较Table 1 Comparison between the central film thickness of the modified formula and numerical results

4 结论

在等温稳态椭圆接触弹流润滑条件下，研究了油膜压力和油膜厚度随椭圆比的变化规律.对比中心膜厚的数值计算值和Hamrock-Dowson公式计算值，得到如下结论：

a.在无量纲载荷一定时，随着椭圆比的增加，中心膜厚先增加后减小，润滑状态从弹流润滑转变到动压润滑.

b.中心最大Hertz压力一定时，随着椭圆比的增加，Hamrock-Dowson公式计算出的中心膜厚出现了与物理相悖的现象，体现在ke≈4.6之后，端泄因子esl为ke的减函数.

c.依据数值计算结果拟合出关于构造参数θ的修正端泄因子和修正Hamrock-Dowson公式，并检验了公式精度，两者吻合度良好.

符号说明