巧建坐标系 速解斜面上的抛体运动问题

何仕乾

摘 要：斜面上的抛体运动问题，初速度主要涉及两个特殊方向，水平方向和与斜面垂直的方向.初速度与斜面垂直的问题，选取不同的坐标系，解答过程繁简差异极大.若结合各自的优势，则可高效解答此类问题.

关键词：斜面;抛体运动;解法;优化

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2022）01-0118-03

抛体运动是曲线运动的一种特殊情形，是研究曲线运动规律和方法的例子.抛体运动，涉及运动的合成与分解.教材中重点学习了平抛运动.平抛运动的处理方法，一般将其分解为水平方向的匀速直线运动和竖直方向的自由落体运动.实际教学中，试图通过平抛运动的重点学习，希望学生能“举一反三”，能够用类似的规律和方法处理其它方向的抛体运动.

斜面上的抛体运动，一般只涉及初速度方向水平的情形.抛出的物体若落在斜面上，用速度偏向角与位移偏向角的关系解答相关问题，若落在水平面上，则按一般的平抛运动解答即可.笔者在教学中，经常遇到学生探讨初速度方向不水平的问题.在指导学生解答相关问题时，若学生建立不同方向的坐标系，解答过程涉及的运算量相差较大.如何优化解法，提高效率，下面從一道典型习题说起.

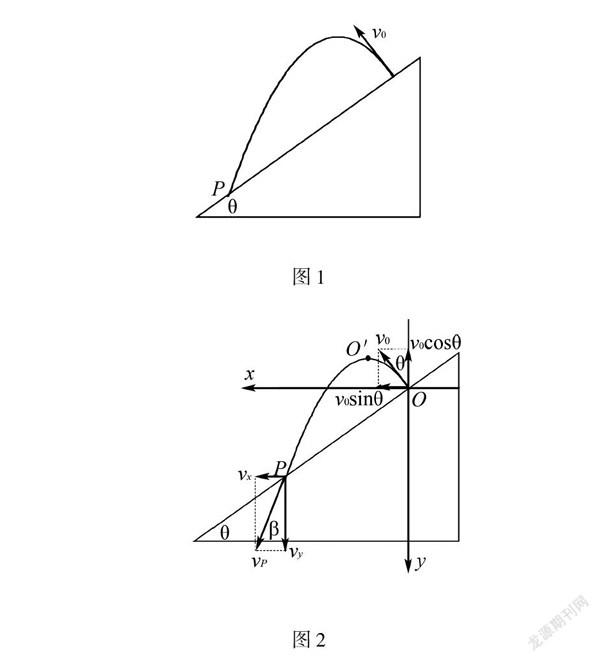
问题 如图1所示，在一倾斜角为θ，足够长的斜面上，垂直斜面向上以v0抛出一小球（可视为质点），不计空气阻力，试求小球落在斜面上时的速度.

解法1 以抛出点为坐标原点，建立如图2所示坐标系，相对x坐标轴，小球做斜抛运动.将小球的运动分解为水平方向和竖直方向两个分运动.即水平方向以vx=v0sinθ为初速度做匀速直线运动，竖直方向以vy=v0cosθ为初速度做竖直上抛运动.

令历时t小球落到斜面上P点，则

x=（v0sinθ）t，

y=-（v0cosθ）t+12gt2.

由于tanθ=yx

则有：t=v0cosθg

在p处，沿y方向的速度为vy=-v0cosθ+gt=v0（2cosθ-cosθ）

合速度为vp=v2x+v2y=（v0sinθ）2+v20（2cosθ-cosθ）2=v01+4tan2θ

与水平方向的夹角为β，则

tanβ=vyvx

=v0（2cosθ-cosθ）v0sinθ

=1+sin2θsinθcosθ.

解法2 如解法1，仍以抛出点为坐标原点，建立如图2所示坐标系，由数学知识可知，小球落在P点，即在xoy坐标系中，斜面所在的直线与小球轨迹形成的抛物线交于P点.

斜面所在直线方程为y=xtanθ①

抛物线的方程，由竖直上抛运动可知，顶点O′的

纵坐标为y′=-（v0cosθ）22g，

上升到O′的时间为t′=v0cosθg，顶点O′横坐标为x′=（v0sinθ）×v0cosθg=v20sinθcosθg.

当在O′点以水平速度vO′平抛小球时，其抛物线方程为y′=g2v2O′（x′）2.

综上，可列出小球运动轨迹抛物线方程为

y=g2（v0sinθ）2（x-v20cosθsinθg）2-（v0cosθ）22g ②

联立①②可得x2-2v20tanθgx=0

解得：x=0（初始抛出点舍去），

x=2v20tanθg.

从O点到P点，水平方向匀速运动，令历时为t，则

t=xvx=2v0gcosθ

在p处，沿y方向的速度为

vy=-v0cosθ+gt=v0（2cosθ-cosθ）

合速度为vp=v2x+v2y=v01+4tan2θ

与水平方向的夹角为β，则

tanβ=1+sin2θsinθcosθ

解法3 沿斜面方向和垂直斜面方向，建立如图3所示坐标系，则小球的运动可看作两个分运动：

沿x方向的初速度为v0，加速度大小为ax=gcosθ的匀减速直线运动，沿y方向初速度为0，加速度大小为ay=gsinθ的匀加速直线运动.

小球从抛出到落在斜面上的时间，可由x方向的运动求出.在x方向上，相对于斜面，类似竖直上抛运动，小球离开斜面减速至0，又反向加速回到斜面的时间相等，即有t=2×v0gcosθ=2v0gcosθ.回到斜面p点时，沿x负方向的速度大小为vx=v0.

打在p点时，沿y方向的速度即为

vy=ayt=（gsinθ）×2v0gcosθ=2v0tanθ

p点速度大小为：

vp=v2x+v2y=v20+（2v0tanθ）2=v01+4tan2θ

令vp与y轴的夹角为α，则tanα=vxvy=12tanθ

与水平方向的夹角为β，则β=α+θ.

tanβ=tan（α+θ）=sin（α+θ）cos（α+θ）

由tanα=12tanθ

不难得到sinα=11+4tan2θ和cosα=2tanθ1+4tan2θ

则有tanβ=1+sin2θsinθcosθ.

总结 此例中，由于初速度方向与重力加速度方向夹角不特殊，需要对涉及的两个矢量进行分解.分解不同矢量，在解答过程中涉及的运算量相差很大，对学生运用数学解决物理问题的要求较高.抛体运动相关知识是高一教学内容，对于高一学生，此例中涉及的数学运算对他们而言有难度，解法1将竖直方向的分运动整体考虑，实际教学中学生也不易掌握，他们更愿意将竖直上升过程和自由下落过程分段处理，这些需要在学生处理过程中进行引导和点拨.

比较以上解法，关键在求解小球离开斜面的时间（空中运动时间），解法3选择斜面为参考面，分解重力加速度无疑是快、准、稳.求得时间后，在确定P点速度大小和方向时，解法1优势明显.解法2对于数学能力较强的学生可尝试，“技多不压身”，多一种方法，多一分能力.

本例初速度方向与斜面垂直，虽然情形仍然特殊，但对于高中阶段的学习，已属于较高要求.当初速度方向与斜面夹角不是特殊的垂直关系时，由上述两种解法可知，仍然可由解法3求空中运动时间，由解法1确定落点处的水平方向和竖直方向分速度，从而求得落点处合速度的大小和方向.

参考文献：

[1]人民教育出版社，课程教材研究所.普通高中课程标准实验教科书（物理必修2）[M].北京：人民教育出版社，2004（5）.

[责任编辑：李 璟]