模型为媒 思维为翼 能力为核

陈伟震

摘 要：匀变速直线运动规律是高中物理学习的重要内容.本文以汽车运动为载体，以生活情境构建物理模型，通过几种运动模型，培养学生分析实际问题的能力，提升学生的核心素养.

关键词：匀变速直线运动规律;核心素养;模型

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2022）01-0106-03

《普通高中物理课程标准》中指出，学生发展核心素养是指学生在接受相应学段的教育逐渐发展起来的适应个人终身发展和社会发展需要的必备品格和关键能力.模型构建是科学思维的核心要素.以生活情境构建物理模型，对相关物理知识进行深度加工，提升对情境物理模型的问题解决能力.

匀变速直线运动是高中物理学习的基础.其中有很多规律.

采用常规的教学方式，背公式，用公式，在物体，小球等模型中解决问题，更多的关注于学生的认知领域，忽视了“学科核心素养”的培养.最终学生只是获得了课堂上物理学科知识.这样的物理教学必然忽视了学生在个人内省领域及信息处理领域的发展.要想促进核心素养在物理课堂教学中落地，必须以物理核心素养培养为基石，以发展学生核心素养为导向，贴近学生的自身实际发展探究能力和实践意识，将学生培养成为符合社会要求，全面发展的的创新型人才.

在教学中，笔者以学生所熟知的汽车运动为载体，设计几种汽车做匀变速直线运动的情况，学生构建出相应的物理模型.在此基础上利用相关的匀变速直线运动规律解决问题，引导学生在内省中思考，有意识地引导学生在更深层次理解物理规律，提升解决实际问题的能力.

1 “疲劳驾驶”模型

疲勞驾驶是一个很严重的社会问题.疲劳驾驶主要是延长了人的反应时间，对突发事件反应不及时，很容易酿成车毁人亡的事故.对于疲劳驾驶，学生只是有基本的了解.如果能在具体的情境中，给予具体的数据进行计算，这样既培养了他们建立物理模型的能力，对疲劳驾驶的危害有更具体的认识，也提升了社会责任感.

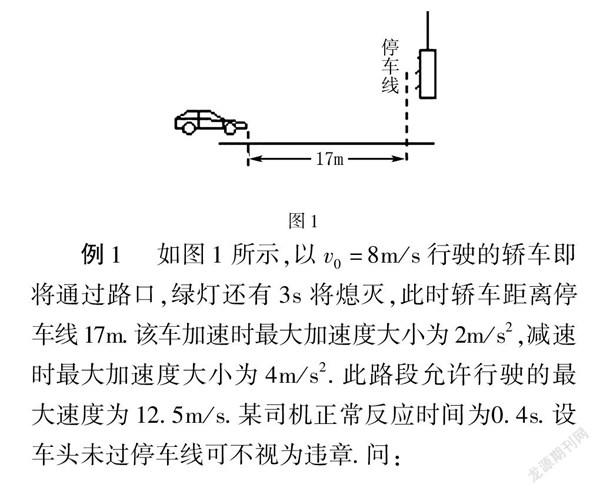
例1  如图1所示，以v0=8m/s图1行驶的轿车即将通过路口，绿灯还有3s将熄灭，此时轿车距离停车线17m.该车加速时最大加速度大小为2m/s2，减速时最大加速度大小为4m/s2 .此路段允许行驶的最大速度为12.5m/s.某司机正常反应时间为0.4s.设车头未过停车线可不视为违章.问：

（1）这位司机打算加速前进，他能否在绿灯熄灭前通过停车线？

（2）若司机疲劳驾驶驾驶，反应时间变为原来的3倍，分析他是否会闯红灯？

解析 （1）司机在绿灯熄灭前行驶的位移：

汽车在反应时间内行驶的位移 x1=v0t1=8×0.4=3.2m

在加速时行驶的位移x2=v0t1′+12a1t′21=8×（2-0.4）+12×2×（2-0.4）2=15.36m

此时轿车的速度为v=v0+a1t1′=8+2×（2-0.4）=11.2m/s<;12.5m/s，轿车末达到最大速度.

故总位移x总1=x1+x2=18.56m>17m， 所以汽车能在绿灯熄灭前通过停车线.

（2）司机在酒后驾驶，则汽车在反应时间内行驶的位移x3=v0t3=8×0.4×3=9.6m

在加速时行驶的位移x4=v0t2′+12a1t′22=8×（2-1.2）+12×2×（2-1.2）2=7.04m

x总2=x3+x4=16.64m<17m

所以汽车不能在绿灯熄灭前通过停车线，

若司机想在停车线前停车，采取减速，则

x5=v202a2=822×4=8m，

则汽车减速运动的总位移

x总2′=9.6+8=17.6m>17m

所以汽车不会在停车线前停下.因此司机无论采用加速还是减速都必然会闯红灯.

以“疲劳驾驶”为模型载体，学生不再是死记硬背套公式，而是提升学生对实际情境的建模能力，使物理核心素养的物理物理观念、科学思维、科学探究科学态度与责任等由理论走向教学实践.

2 “刹车问题”模型

汽车刹车模型，一般是利用基本规律解决问题.如果是减速为零则时可以采用逆向思维利用初速为零的匀加速直线运动的特殊规律.

例2 北方的冬天空气污染重.有一辆轿车在一个雾霾天气中以20m/s的速度匀速行驶，司机突然模糊看到正前方路口有一个老人在过马路，他立即刹车，刹车后加速度大小为5m/s2，则 （  ）

A.经4s 汽车速度变为零

B.汽车刹车后的位移为40m

C.汽车在第4s末、第3s末、第2s末的速度之比为3∶2∶1

D.汽车第一个1s内，第二个1s内，第三个1s内，第四个1s内位移之比为1∶3∶5∶7

解析 汽车做减速运动，利用逆向思维，将汽车看成初速为零，以大小为5m/s2的加速度做匀加速运动较简单.在实际情境中对相关物理知识进行深度加工，建立合理的物理模型，运用正确的规律，提升了问题解决能力.

例3 一汽车以某一速度在平直公路上匀速行驶.行驶过程中，司机忽然发现前方有一警示牌，立即刹车.刹车后汽车立即开始做匀减速直线运动，直至停止.已知从刹车开始计时，汽车在 0～2s内的位移大小为48m，4s～6 s内的位移大小为3m.用v、a分别表示汽车匀速行驶时的速度大小及刹车后的加速度大小，则（  ）.

A.a=458m/s2，v=2378m/s

B.a=323m/s2，v=1043m/s

C.a=8m/s2，v=32m/s

D.a=6m/s2，v=30m/s

分析 汽车刹车时可看成做匀减速运动.很多学生误认为在所给定的时间内均做匀减速运动，而得到错误答案.实际上汽车可能在所给定的时间内提前停下.这时可以采用假设法判断出实际运动

情况.

解析 设汽车的加速度大小为a，初速度为v0，则在0～2s内，t=2s的位移为：

x1=v0t-12at2①

汽车在4s时的速度为v=v0-4a②

则4～6s内的位移为：x2=vt-12at2

代入数据解得：v0=29.625m/s，a=5.625m/s2;

但当t=6s时，可得速度为v6=-4.125m/s，这说明在t=6s时汽车已停止运动，因此上面的计算不成立.则4～6s内的位移为

0-v2=-2ax2③

联立①②③式计算可得

a=6m/s2，v0=30m/s

另一解a=323m/s2，v=1043m/s舍去.因为此解在4s之前汽车速度就变为零.故D正确，ABC错误.

本题在考虑在t=6s时汽车已停止运动的情况下得到两组a与v的数值，需要作出判断.有助于培养学生利用物理知识进行分析判断，解决实际问题的能力.

3 追及与相遇问题模型

追及与相遇问题，在高考中时有出现.在实际教学中，当问题稍微复杂一点，就不知道合理利用模型分析与解决问题.例如两车出发的位置不同，两车出发的时间不同，同时存在加速、减速或匀速的运动种类.解决问题的办法可以做出运动过程的示意图，写出两个物体位移的关系式，通过求解时间来解决问题.也可以利用v-t图像来解决问题.其中利用v-t图像来解决问题这种思维方式更直观，简单.

例4 高速公路超车道的限速为100km/h～120km/h.某日该车道上有汽车A和汽车B以相同速度匀速行驶，A在B后方106m.B司机突然发现前方有交警测速，B车立即以a=5m/s2的加速度开始刹车，A车司机则在B开始刹车的1s后做出反应，以恒定加速度a1刹车.一段时间后A车司机发现可能会撞车，立即启用紧急制动，将加速度大小提高至a2=8m/s2，但依然撞到了B车上.调查监控得知，A车的两段刹车时间分别为8s和1s，现场勘测得知，A车紧急制动的位移为6m.所有刹车过程均视为匀减速直线运动.求：

（1）A车撞上B车时的速度;

（2）通过计算判断两车是否超速.

（3）经调查，事故原因为A车司机超速且疲劳驾驶，导致反应时间过长，判断失误，操作不当.若A车装有自动刹车系统，在B车刹车0.3s后即作出反应并以8m/s2的加速度緊急制动.请通过计算判断这种情况下车祸是否会发生.若发生，求A车撞上B车时的速度;若不发生，求两车的最近距离.

解析 （1）设A车启用紧急刹车时的速度为v1，由运动学公式可知x=v1t-12a2t12

代入x=6m，a2=8m/s2，t1=1s

可得v1=10m/s

故A车撞上B车时的速度v2=v1-a2t1=10m/s-8×1m/s=2m/s

（2）设两车的初速度为v0，由于A车的两段刹车时间分别为8s和1s，再加上A车司机的反应时间为1s，所以B车刹车的总时间为t=1s+8s+1s=10s，由于A、B相撞，可知位移关系为

xA=xB+106

xA=v0×1+v0+v12×8+6

xB=v0t-12at2

代入解得v0=38m/s=136.8km/h 超速

（3）设两车在B车刹车t0=0.3s后经过时间t2达到相同的速度v，

对甲车，有v=v0-a2t2

对乙车有v=v0-a（t2+0.3）

联立二式解得 t2=0.5s，v=34m/s，作出甲乙刹车过程的v-t图像

可以求得阴影部分表示的位移为

Δx=12×0.3×4=0.6m

即两车不发生碰撞.最近距离为106-0.6=105.4m

物理教学的目的不仅仅是为了得到答案，而是要注重通过问题解决促进核心素养的达成，要将“情境线”、“模型线”、“知识线”、“问题线”相结合，有利于培养学生在真实情境中的问题解决能力.在问题解决中进一步提高探究能力，促进物理学科核心素养的形成.

参考文献：

[1]李学智.核心素养模式下的高三一轮复习——以“匀变速直线运动”为例[J].教学考试，2019（49）：7-10.

[责任编辑：李 璟]