一类非线性时滞双曲型分布参数系统的振动条件
罗李平, 曾云辉, 罗振国
(衡阳师范学院 数学与统计学院,湖南 衡阳 421002)
随着现代科技的发展, 人们发现在人口动力学、化学反应过程、通讯工程、机器人、环境系统、生态系统、社会系统等领域的实际问题中, 系统许多现象的出现或改变并不是瞬间完成的, 在它们的数学模型中含有各种滞后量(特别是时间滞后量), 这些现象的数学模型往往可归结为时滞分布参数系统。由于时滞分布参数系统充分考虑到历史因素(即滞后量)对系统的影响, 故能更精确地描述实际现象。因此, 有关时滞分布参数系统的理论及其应用等问题引起国内外学者的广泛关注。振动性理论作为时滞分布参数系统理论的重要分支之一, 在自然科学、工程技术及社会生活中都是有现实意义的, 如控制系统中的自激振动、同步加速器中波束的振动、化学反应过程中的复杂振动、火箭发动机燃烧时产生的振动、建筑物和机器的振动、工业中电磁开关触头的振动、乐器发出的振动、地震中的振动等都可以用一些分布参数系统模型来刻画, 通过研究相应系统的振动性, 就可对振动加以合适的控制使之对人类产生有益的影响, 具有重要的应用价值。 近年来, 许多学者对时滞分布参数系统的振动性问题进行了研究和探讨, 并取得了许多很好的成果[1-10]。本文则讨论下列一类特殊的非线性时滞双曲型分布参数系统式(1)在第三类边值条件式(2)下解的振动性质, 获得了判别其一切解振动的不需要利用Robin特征值问题的新的充分性条件, 结论充分表明了时滞对系统振动性的影响。
utt=a(t)h(u)Δu-p(x,t)f{u[x,τ(t)]},
(x,t)∈Ω×R+≡G
(1)
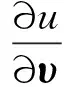
(2)
式中:Ω⊂Rm为有界区域; ∂Ω为逐片光滑; Δ为Rm中的m维Laplace算子;R+=[0,∞);υ为∂Ω的单位外法向量;β(x)∈C[∂Ω,(0,∞)]。
在本文中, 我们总假定下列条件成立
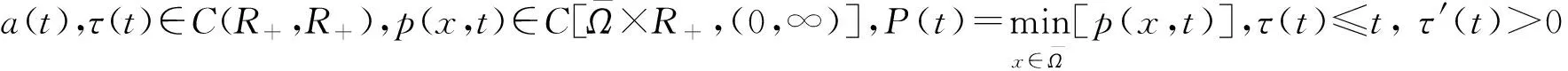
条件2h(u),f(u)∈C(R,R),uh′(u)≥0, 且对u≠0有f(u)/u≥M=const.>0。
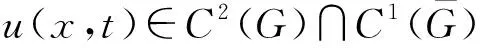
以下我们总假设边值问题式(1)和式(2)的解是整体存在的。
1 主要结果及其证明
考虑集合D0={(t,s)∶t>s≥t0},D={(t,s)∶t≥s≥t0}。
若H∈C(D,R)满足条件:(ⅰ)H(t,t)=0,t≥t0;H(t,s)>0, (t,s)∈D0;(ⅱ)H在D0上对第二个变量s有连续且非正的偏导数。则称函数H具有性质P。
定理1设下述条件成立:
条件3存在函数H具有性质P,h∈C(D0,R),k,ρ∈C1[[t0,∞),R+], 使
(3)
若
(4)
则边值问题式(1)和式(2)的所有解在G内是振动的。
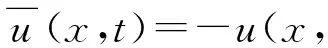
将式(1)两边同时对x在Ω上积分有
(5)
由Green公式、边值条件式(2)及条件2有
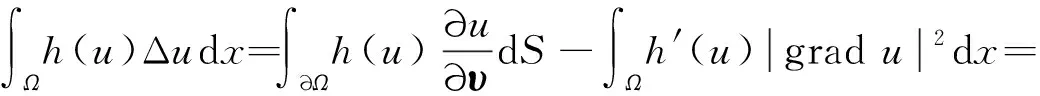
(6)
式中, dS为∂Ω上的面积元素。
又由条件1和条件2有
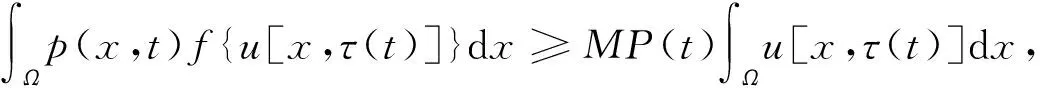
(7)
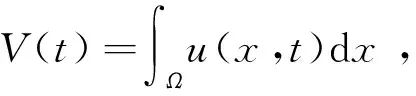
V″(t)+MP(t)V[τ(t)]≤0,t≥t1
(8)
于是由式(8)可知,V″(t)≤0,t≥t1, 即V′(t)在区间[t1,∞)上单调减少。由此不难推得
V′(t)>0且V′(t)≤V′[τ(t)],t≥t1
(9)
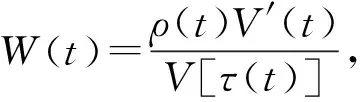
(10)
式(10)两边同乘以H(t,s)k(s), 对s从t1~t(≥t1)积分可得
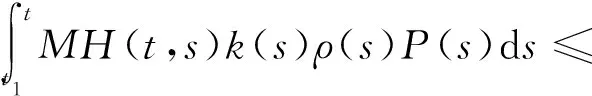
于是由(ⅱ)可得

因此有
从而有
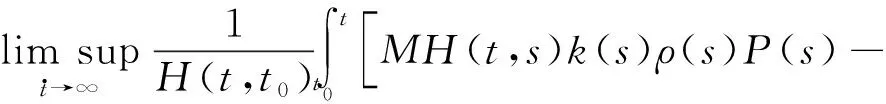
这与式(4)相矛盾。定理1证毕。
作为定理1的直接结果, 我们有如下推论。
推论1若定理1中的条件式(4)用如下条件替换
且
则边值问题式(1)和式(2)的所有解在G内是振动的。
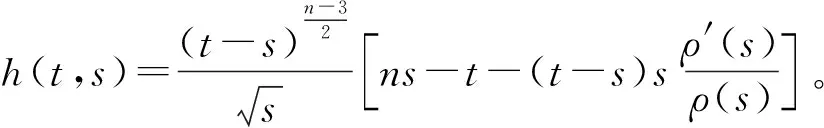
推论2若存在ρ∈C1[[t0,∞),R+], 整数n>2使得
则边值问题式(1)和式(2)的所有解在G内是振动的。
注2利用本文的思想, 我们还可以考虑其他边值条件。譬如, 考虑如下的第一类边值条件
u=0,
(x,t)∈∂Ω×R+
(11)
我们不难得到边值问题式(1)和式(11)的若干振动判据。限于篇幅, 在此省略之。
2 应用举例
下面通过一个实例来说明本文主要结果的有效性。
例1考虑双曲型分布参数系统
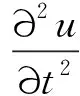
(12)
边值条件为
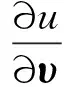
(13)
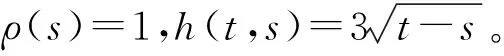
3 结 论
本文讨论了一类带时滞的非线性双曲型分布参数系统在Robin边值条件下解的振动性问题, 建立了判别其所有解振动的不需要利用特征值定理的新的充分条件, 所得结论充分表明时滞对系统振动性的影响, 这些结论对工程上的机械减振和降噪等实际应用具有重要的理论指导意义。

