基于自适应滤波算法的信号处理研究

李忠政, 董昱廷, 曹新慧, 周二彪, 付林

(国网新疆电力有限公司， 经济技术研究院， 新疆， 乌鲁木齐 830002)

0 引言

波达方向(DOA)估计在声纳、雷达、通信和导航系统中有着广泛的应用[1-3]。传统的基于子空间分解的DOA估计方法，即多信号分类(MUSIC)[4]和基于旋转不变性技术[5]的信号参数估计，因其良好的性能而受到广泛的关注。然而，这些方法需要借助空间协方差矩阵的特征值分解(EVD)，使得计算量较为庞大[6]。此外，这些方法还需要估计信源的数量。文献[7]中提出了各种优化方法来最小化传统方法的计算复杂度，虽然在一定程度上降低了计算复杂度，但仍然需要近似协方差矩阵的EVD。为了克服子空间分解方法的复杂性问题，文献[8]提出了一种基于固定步长最小均方差算法(FSS-LMS)的DOA估计方法，该方法计算效率高，但是很难选择固定步长的合适值。

本文提出了一种基于变步长最小均方差算法(VSS-LMS)的DOA估计方法。通过使用估计的误差信号来更新步长。通过阵列模式的倒数得到空间频谱，其中峰值表示信号的DOA估计，该方法不需要EVD和信源数量的估计，且具有计算复杂度低的优点。

1 信号模型

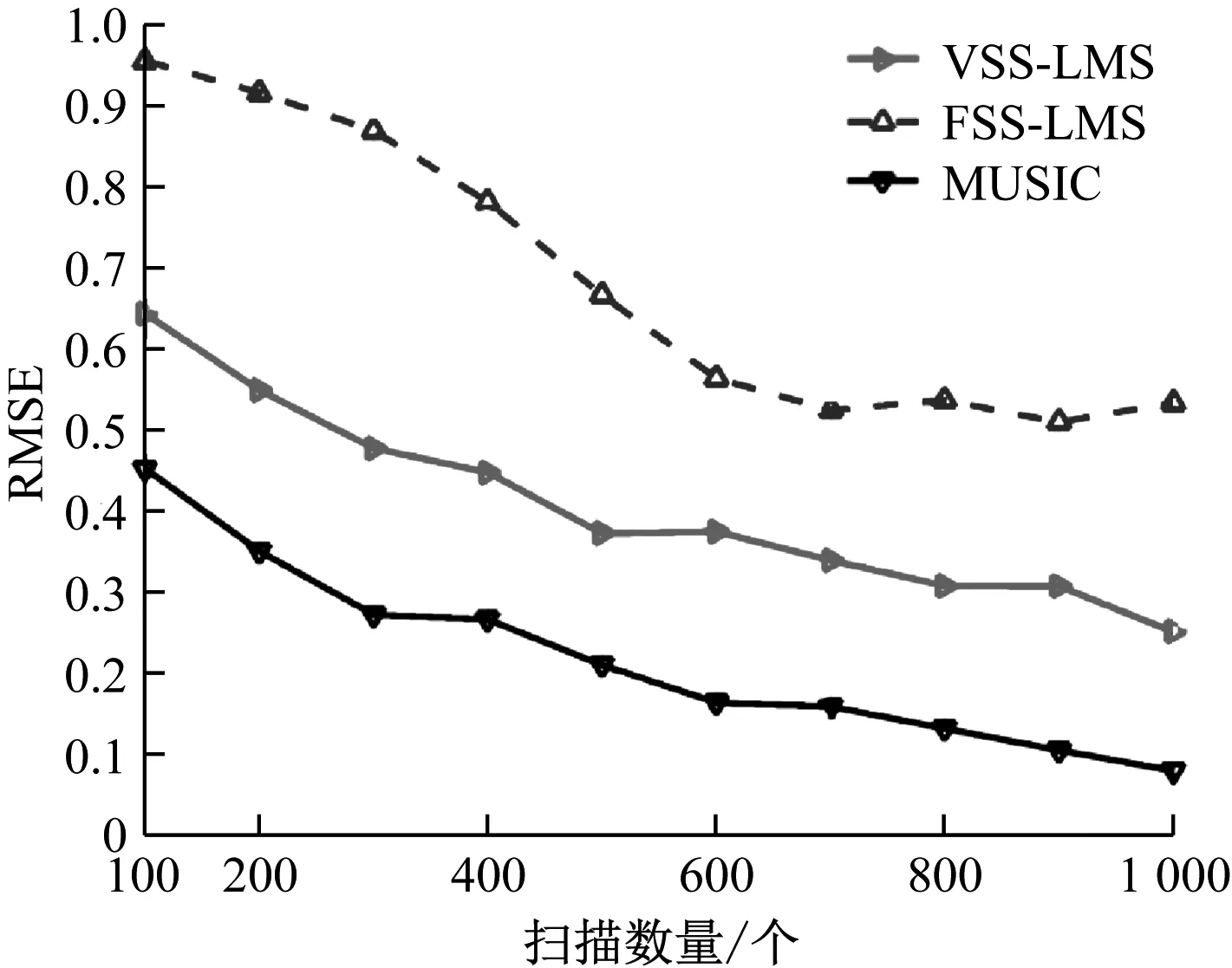
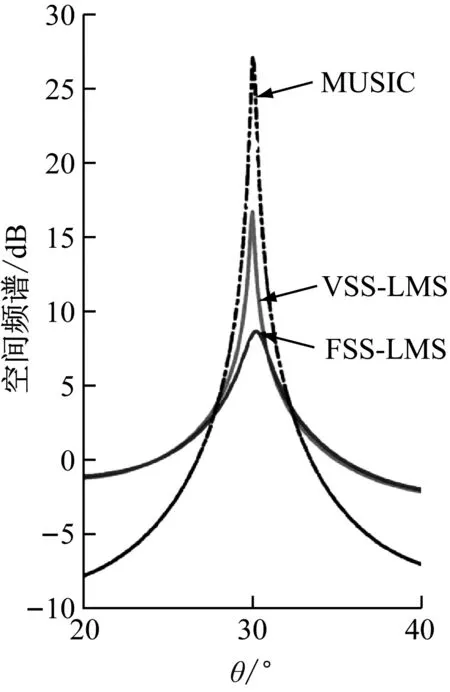
考虑N个具有半波长间距的全向天线阵元的均匀线性阵列(ULA)，假设在θ=[θ0,θ1,…,θM-1]个方向上具有K个射入波将M(M

(1)

其中，sm(k)为对应的信号包络，m=0,1,…,M-1，a(θm)为该形式的阵列方向向量，v(k)和a(θm)=[1,ejπsin θ1,…,ejπ(N-1)sin θM-1]为零均值的加性高斯白噪声。式(1)的矩阵形式可以表示为式(2)：

X(k)=Asm(k)+V(k)

(2)

(3)

(4)

图1 自适应天线阵列原理图

2 可变步长最小均方差(VSS-LMS)算法

本文推导了基于可变步长最小均方差(VSS-LMS)算法的DOA估计方法。利用递归方法[9]计算辅助阵元的权重向量如式(5)：

(5)

其中，μvss(k)为可变步长。其算法如式(6)，

(6)

(7)

(8)

(9)

其中，(·)H为共轭转置。可以根据式(6)自适应地选择步长，在初始阶段得到较大的步长，加快了收敛速度，当收敛到最优解时，得到较小的步长，保证了稳定性和较低的均方误差。在得到最佳权重向量后，其阵列模式为式(10)：

G(θ)=wHa(θ)

(10)

(11)

3 仿真分析

本文通过数值仿真验证所提方法的性能。在这些仿真中，考虑具有半波长间隔的8个阵元的ULA。从30°和60°接收到信噪比(SNR)分别为10 dB和20 dB的互不相关信号。FSS-LMS方法的步长为2×10-5。通过Monte Carlo模拟获得空间频谱，而均方根误差(RMSE)通过平均200次Monte Carlo模拟计算得出。

本文所提VSS-LMS算法的计算复杂度与文献[8]的FSS-LMS算法和文献[10]的MUSIC算法进行了比较，结果如表1所示，其中L为待扫描的角度值。通过500次扫描不同阵元数量的计算复杂度，如图2所示。

表1 不同DOA估计方法的计算复杂度

图2 不同阵元数量的计算复杂度

表1和图2的结果表明，本文所提出的VSS-LMS算法的计算复杂度远低于MUSIC算法，与FSS-LMS算法的计算复杂度几乎相同。

对于8个阵元的ULA，通过500次扫描条件下，SNR分别为10 dB和20 dB时，不同扫描角度的空间频谱结果见图3。

(a) 扫描角度为30°时 (b) 扫描角度为60°时

图3的结果表明，本文所提出的VSS-LMS算法能够较准确地估计信号的DOA，并能提供与MUSIC方法相似的窄峰，而FSS-LMS方法不能准确地估计信号的DOA，并且在30°和60°时误差为0.2°。

均方根误差(RMSE)的表达式如下，

(12)

对于8个阵元的ULA，通过500次扫描条件下，扫描角度从30°至60°时，不同SNR的RMSE比较结果如图4所示。

图4 不同算法SNR的RMSE比较

图4的结果表明，与MUSIC算法相比，本文所提出的VSS-LMS算法的RMSE随着SNR的增加而迅速减小，但其性能优于FSS-LMS算法，且接近MUSIC算法。

通过500次扫描条件下，扫描角度从30°至60°，SNR为15 dB，不同阵元数量的RMSE比较结果如图5所示。

图5 不同阵元数量的RMSE比较结果

图5的结果表明，本文所提出的VSS-LMS算法的性能明显优于FSS-LMS算法，接近于MUSIC算法。

对于8个阵元的ULA，扫描角度从30°至60°，SNR为15 dB，不同扫描数量的RMSE比较结果如图6所示。

图6的结果表明，本文所提出的VSS-LMS算法的性能也明显优于FSS-LMS算法，而MUSIC算法的性能略优于本文方法，但计算复杂度远低于MUSIC算法。

4 总结

本文提出了一种基于VSS-LMS算法的DOA估计方法。利用估计出的误差信号推导出步长，改进了传统固定步长方法。通过阵列模式的倒数得到空间频谱，其中的峰值表示信号的估计DOA。仿真结果验证了本文方法的有效性。实验结果表明，基于VSS-LMS算法的DOA估计方法能以较低的计算复杂度实现较好的性能。

图6 不同扫描数量的RMSE比较结果