基于改进时空残差卷积神经网络的城市路网短时交通流预测

包银鑫，曹 阳，2，施 佺，2*

（1.南通大学信息科学技术学院，江苏南通 226019；2.南通大学交通与土木工程学院，江苏南通 226019）

0 引言

随着我国城市化进程的加快，交通基础设施得到极大的改善。然而，汽车数量的日益增长，导致城市交通拥堵问题越发严重。实时准确地获取城市交通流信息，对出行者和交通管理部门具有重要意义［1］。近些年来，研究人员尝试了多种方法来提高交通流的预测精度。这些方法大体分为两类：模型驱动方法和数据驱动方法［2-3］。

模型驱动方法也称为参数方法，该方法根据数学理论假设预先确定模型，用少量数据去拟合模型，实现交通流预测目的。这种方法存在模型结构固化、假设情况与实际交通状态不符等问题，导致预测模型在实际应用中预测精度不高。常用的有时间序列模型［4］、卡尔曼滤波模型［5］等。与模型驱动方法不同，数据驱动方法可以很好反映交通数据的不确定性，数据驱动方法分为传统机器学习方法和基于深度学习的方法。传统机器学习方法中的支持向量机（Support Vector Machine，SVM）［6］、贝叶斯模型［7］、K最近邻（K-Nearest Neighbor，KNN）［8］等都被用于交通流预测。尽管传统机器学习相比模型驱动方法可以从交通数据中学习统计规律，但处理高维度复杂数据时预测精度会大打折扣［9］。

随着深度学习的兴起，具有高维数据处理和非线性数据特征挖掘能力的深度神经网络模型受到越来越多研究人员的青睐。Lv 等［10］在实验中证明了基于深度学习架构的神经网络对高维数据的处理能力。Polson 等［11］证明深度神经网络比单隐藏层的神经网络更能捕捉交通状态的非线性。此外，深度置信网络（Deep Belief Network，DBN）［12］、时滞神经网络（Time Delay Neural Network，TDNN）［13］也被用于交通流预测。城市路网每一个区域的交通流会受到相邻区域和上一个时间段的交通流影响，上述模型每次只能提取部分区域的交通流信息，仅依靠部分区域的信息来预测交通流远远不够。

计算机视觉和图像识别领域的发展，推动了深度卷积神经网络的发展，卷积神经网络（Convolutional Neural Network，CNN）可以通过卷积算子实现对图像空间特征的捕获［14］，这一特性启发研究人员考虑使用卷积算子挖掘交通流的空间特性，Ma 等［15］将交通网络利用灰度算子转化为灰度图像，将图像转化为二维时空矩阵来预测交通速度，该模型虽有效捕获了交通流空间特征，但忽视了交通流的时间特性。循环神经网络（Recurrent Neural Network，RNN）被广泛用于处理交通流时间特性，王祥雪等［16］使用RNN 对交通流情况进行预测，但RNN 容易受到梯度消失的影响，难以捕获长期时间特性。因此，RNN 的改进模型长短期记忆（Long Short-Term Memory，LSTM）网络［17］和门控递归单元（Gated Recurrent Unit，GRU）网络［18］常被用于交通流预测。RNN 及RNN 改进模型有效捕获了交通流的时间特性，但无法捕获交通流的空间特性。为充分挖掘交通流的时间和空间特性，考虑交通流时间和空间信息的时空混合模型ConvLSTM（Convolutional LSTM）［19］被提出来，相较于仅考虑单一特性的预测模型提高了交通流的预测精度。由于混合模型结构的复杂性，模型的训练会随着网络层数的增加而变得困难，He 等［20］针对网络深度增加而模型训练精度下降的问题，在深度网络结构中引入残差单元提高模型的训练精度。Zhang 等［21］在交通流预测中引入时空残差网络（Spatio-Temporal Residual Network，ST-ResNet），该方法将城市划分为时空栅格矩阵，利用卷积操作和残差搭建ST-ResNet 模型，提高模型的时空间依赖性。Guo 等［22］在ST-ResNet 网络的基础上引入两种时间模式，提高了模型对时空特性的自动捕获能力。Guo 等［23］在两种时间模式的基础上，引入天气、节假日等外部因素，实现了交通流动态特征的捕获。赵建立等［24］和Zheng 等［25］分别通过改进残差网络的模型结构，实现了交通流预测效果的提升。

如何有效挖掘交通流的时间和空间相关性是交通流的重点研究方向之一。为了充分挖掘交通流的时间相关性和空间相关性，针对传统时空残差模型缺乏对交通流数据进行相关性分析、捕获微小变化容易忽略长期时间特征等问题，本文提出一种基于改进时空残差卷积神经网络的城市路网短时交通流预测方法，实现对周期序列和邻近序列长期时间特征的捕获，从而降低训练误差，提高城市路网短时交通流预测的精度。

1 问题描述

城市路网交通流预测是一个典型的时空序列预测问题，如图1 所示，将城市路网转化成I×J的交通栅格网络，每一个栅格代表一个区域的交通状态，这种状态可以表示当前区域的车流量或者拥挤情况，将栅格网络记作X={xi，j}。将处理后的车辆定位数据按照固定时间间隔统计到每个栅格中，对于每一个位置(i，j)∈R 表示在时间间隔ΔT时，位置(i，j)中的交通状态，将所有I×J位置的观测值都表示成张量Xt∈RI×J。因此，城市网络的交通流预测问题可以转化为交通栅格数据预测问题，给定历史交通栅格数据{Xt|t=0，1，2，…，k}，目标是预测时间间隔k+1 时刻的交通栅格数据Xt+Δk，其中t是给定的最后一条历史数据，Δk是所要预测的时间节点和给定的最后一条历史数据所在时间节点的时间差。

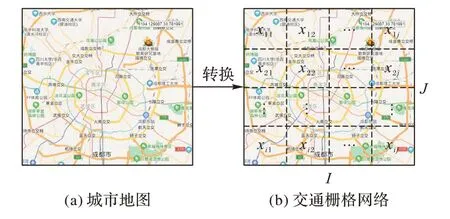
图1 交通栅格数据转化Fig.1 Traffic grid data transformation

2 时空残差模型

城市路网交通流不仅受到相邻时间段交通流的影响，还受到邻接路口的影响，因此城市路网交通流波动具有一定的时间和空间相关性。为了充分挖掘城市路网的时空相关性，本文以传统的时空残差模型作为改进时空残差卷积模型的基本框架。传统时空残差模型主要是由2D 卷积和残差单元构成，其基本结构如图2 所示。利用2D 卷积挖掘路网的空间特征，将2D 卷积与残差单元结合挖掘路网的时间特征，得到时空残差输出Xt，最后通过激活函数得到最终预测值。

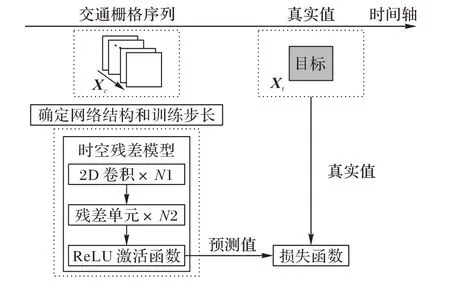
图2 传统时空残差模型结构Fig.2 Structure of traditional spatio-temporal residual model

2.1 2D卷积

交通栅格数据中每个网格的数据都受到邻近网格的影响，不同网格之间具有复杂的空间相关性。使用2D 卷积对空间特征进行挖掘，卷积操作来源于图像处理中的CNN，对图像做卷积操作的目的在于从简单特征中提取复杂特征。将交通栅格数据看作一张二维图片，对其进行卷积操作可以挖掘局部空间特征。其中，2D 卷积特指对二维矩阵进行卷积操作，一般将公式定义为：

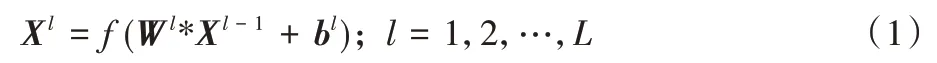
其中：Xl-1为第l层卷积层的输入，Wl为第l层卷积层的卷积核参数，Xl为第l层卷积层的输出，bl为第l层卷积层的偏置项，L为总共需要卷积的层数。图3 为2D 卷积示意图，低层特征维度为4× 4，卷积核维度为3× 3，移动步长设置为1，最后输出维度为2× 2。

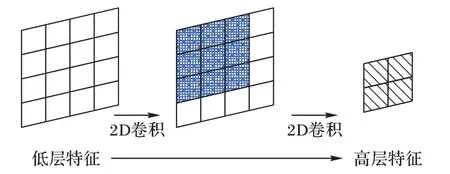
图3 2D卷积示意图Fig.3 Schematic diagram of 2D convolution

2.2 残差单元

堆叠多个2D 卷积可以实现对路网空间特征和时间特征的提取，但随着卷积层深度的增加，模型的训练和精度都会随之下降［21］，因此引入残差单元来提高模型的训练精度。残差单元主要用来突出微小的变化，与2D 卷积结合可以更好地发现时间特征，残差模块结构如图4 所示，残差单元公式定义为：

图4 残差模块结构Fig.4 Structure of residual module

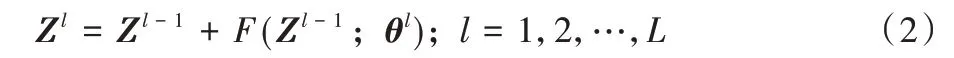
其中：Zl-1为第l层残差单元的输入，Zl为第l层残差单元的输出，θl为第l层残差单元中所有可学习的参数集合，F为残差映射，L为总共需要残差操作的层数。

3 改进时空残差卷积神经网络

针对传统时空残差模型处理城市路网交通流时缺乏对交通流数据进行相关性分析、捕获微小变化容易忽略长期时间特征等问题，提出改进时空残差卷积神经网络。首先，对时间序列引入皮尔逊相关系数的分析，确定相关性高的周期序列和邻近序列；同时，建立周期序列模型和邻近序列模型，引入LSTM 网络作为混合模型提取时间特征，捕获周期序列和邻近序列的长期时间特征；最后，输出加权融合为Xf，通过激活函数得到模型预测值，其改进时空残差卷积神经网络模型结构如图5 所示。

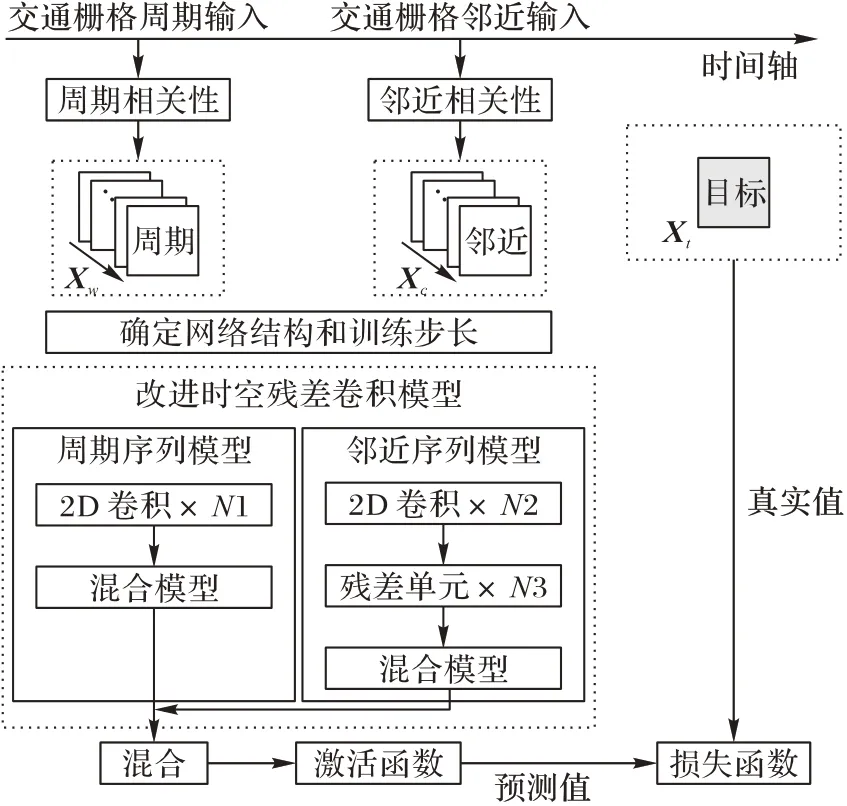
图5 改进时空残差卷积神经网络结构Fig.5 Structure of improved spatio-temporal residual convolutional neural network

3.1 相关性分析

已知一组交通栅格数据序列{Xt|t=0，1，2，…，k}，k是最后一个时间节点。采用皮尔逊相关系数对交通栅格数据进行周期序列和邻近序列的相关性分析，规定周期序列与预测节点Xt的间隔大于1 d，邻近序列与预测节点Xt的间隔小于等于1 d。皮尔逊相关系数公式为：

其中：xi为目标交通栅格数据，yi为待比较的交通栅格数据，σx为目标交通栅格数据的样本总体标准差，σy为待比较交通栅格数据的样本总体标准差。根据皮尔逊相关系数可以将原始交通栅格数据序列划分成周期序列输入Xt-w={Xt-w+1，Xt-w+2，…，Xt-w}，邻近序 列输入Xt-c={Xt-c+1，Xt-c+2，…，Xt-c}。

3.2 混合模型

为了避免残差网络操作后丢失交通栅格数据长期特征，在周期序列模型和邻近序列模型中引入LSTM 网络，LSTM 可以解决RNN 对长期信息依赖的缺失，避免梯度消失和梯度爆炸现象。LSTM 网络结构如图6 所示，通过遗忘门、输入门和输出门实现对数据的输出。其中，遗忘门决定从前边时间状态中丢弃多少信息。输入门决定采取多少新信息输入当前时间状态。输出门决定输出的值。LSTM隐藏单元计算公式为：

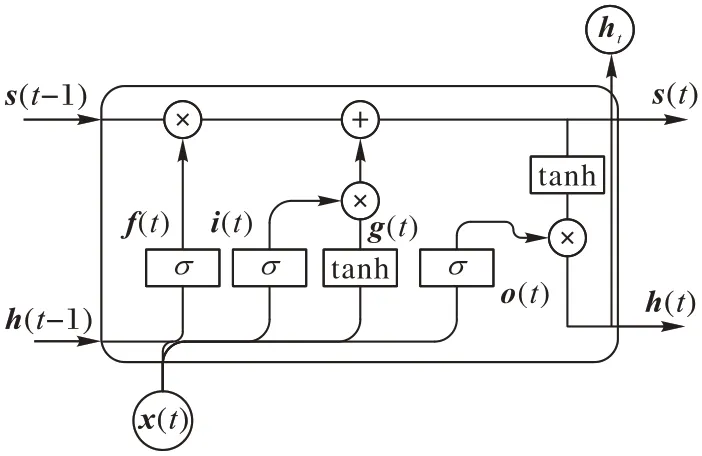
图6 LSTM网络结构Fig.6 Structure of LSTM network

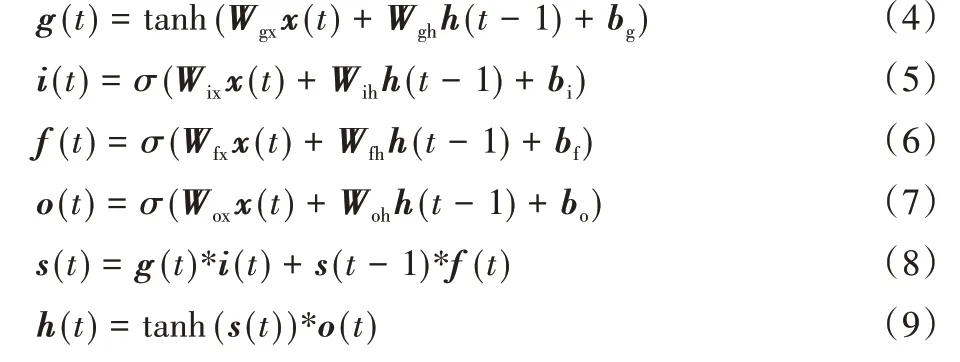
其中：x（t）为当前时刻的输入，h（t）为当前时刻的单元输出，h(t-1)为上一时刻的单元输出，s(t)为当前时刻的单元状态，s(t-1)为上一时刻的单元状态，g(t)为用于描述当前输入的单元状态，f(t)为遗忘门，i（t）为输入门，o(t)为输出门，Wix、Wfx、Wox、Wgx分别为三个门和单元状态的输入层权重，Wih、Wfh、Woh、Wgh分别为三个门和单元状态的隐藏层权重，bi、bf、bo、bg分别为三个门和单元状态的偏置项，σ为Sigmoid激活函 数，σ(x)=1/(1+e-x)，“*”为哈达玛积（Hadamard product）。

3.3 周期序列模型

由于交通流具有明显的周期性，如图7 所示，随着季节的变化，交通流也会呈现出某种趋势变化。为解决上述问题，建立周期序列模型，周期序列模型由两个组件构成，包括2D 卷积和混合模型LSTM，用来学习交通流的周期性特征和趋势，将周期序列模型2D 卷积操作定义为：

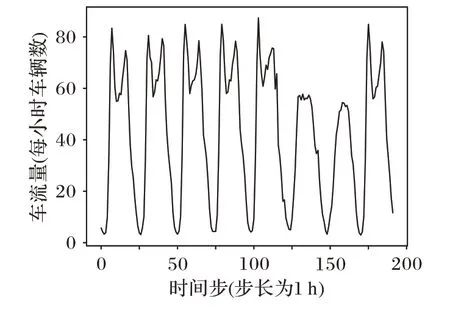
图7 交通流周期性变化Fig.7 Periodic changes in traffic flow

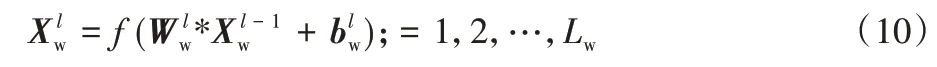
其中：为周期序列模型第l层卷积层的周期序列输入，为周期序列模型第l层卷积层的卷积核参数，为周期序列模型第l层卷积层的周期序列输出，为周期序列模型第l层卷积层的偏置项，Lw为周期序列模型总共需要卷积的层数。

将经过多层2D 卷积操作的输出，输入混合模型LSTM提取长期时间特征，操作定义为：

其中：Xw为周期序列模型的最终输出，LSTMw为周期序列模型的LSTM 操作。

3.4 邻近序列模型

交通流在时间相关性上受到周期性和邻近性的影响，并且邻近性的影响一般更为明显，比如在某个路口发生堵塞，那这个堵塞势必会对一段时间后的交通流产生影响。为解决上述问题，引入邻近序列模型，邻近序列模型由三个组件构成，包括2D 卷积、残差单元和混合模型LSTM，用来学习交通流的邻近性特征，邻近序列模型的2D 卷积操作定义为：

其中：为邻近序列模型第l层卷积层的输入，为邻近序列模型第l层卷积层的卷积核参数为邻近序列模型第l层卷积层的输出为邻近序列模型第l层卷积层的偏置项，Lc为邻近序列模型总共需要卷积的层数。

邻近序列经过2D 卷积操作后，输入到残差单元，残差单元操作为：

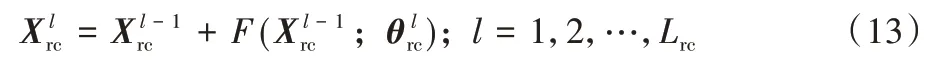
其中：为邻近序列模型第l层残差单元的输入，为邻近序列模型第l层残差单元的输出，为邻近序列模型第l层残差单元中所有可学习的参数集合，F为邻近序列模型的残差映射，Lrc为邻近序列模型总共需要进行残差操作的层数。

为了提高对长期特征的捕获能力，邻近序列经过残差单元输出后，输入到混合模型LSTM 提取长期时间特征，操作定义为：

其中：Xc为邻近序列模型最终的输出，LSTMc为邻近序列模型的LSTM 操作。

3.5 融合

周期序列模型和邻近序列模型的输出分别为Xw和Xc，两种模式在城市交通流中分别具有一定权重，两种模式的权重会随着交通环境的变化而具有不同的比重。在某些环境中，周期序列模型所占的比重较大；而在其他环境中，邻近序列模型所占的比重较大，因此，将两种输出进行加权融合。从历史数据中学习权重值，权重融合后连接激活函数进行输出：

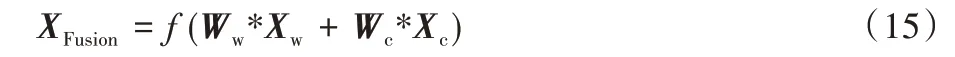
其中：Ww和Wc分别代表周期序列模型和邻近序列模型所占比重，f为激活函数，设置激活函数为Sigmoid 函数。

4 实验与结果分析

4.1 数据集及评价指标

4.1.1 数据来源

数据来源于2014 年8 月3 日到2014 年8 月30 日的成都市出租车经纬度数据，数据全部采集于真实道路，数据获取于百度网盘［26］。该实验数据记录了成都市早上6 点到晚上12 点的出租车运行情况。以成都市绕城公路为边界将成都市城市路网转化为交通栅格网络，进行数据预处理后，将数据映射到栅格网络中，以5 min 为采样间隔，共计生成6 048个交通栅格数据记录，每条记录代表一个时刻的城市路网拥挤状态，一天共有216 个交通栅格数据，共计28 d。在本文中，每个网格状态代表当前区域的拥挤程度，将当前网络中出租车的数量作为拥挤程度的度量。将栅格网络划分为24×24 维度以直观分析区域拥挤情况，具体参数如表1。实验中将前三周的数据作为训练集，最后一周的数据作为测试集。原始数据映射到交通栅格网络的判别函数如下：

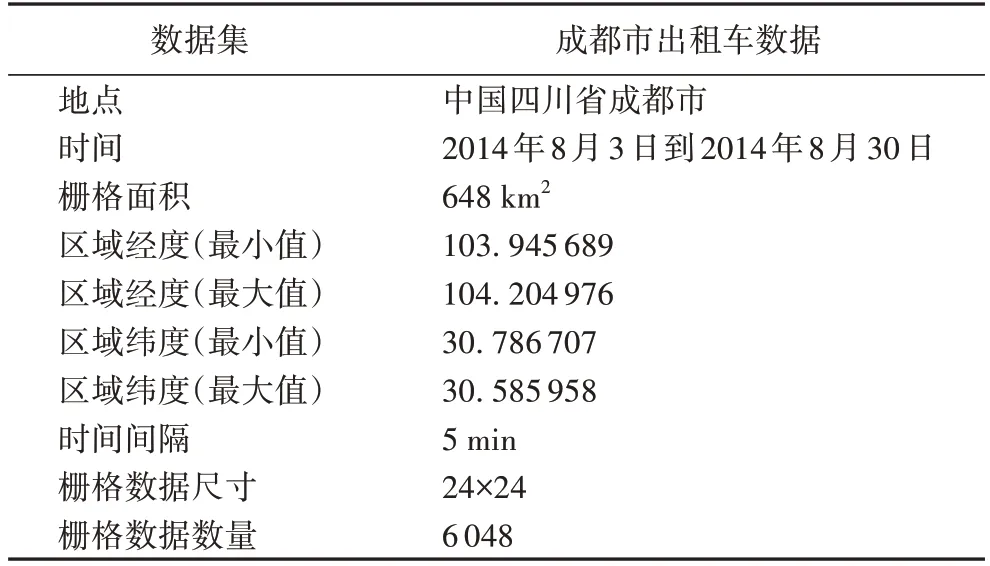
表1 数据集参数Tab.1 Dataset parameters

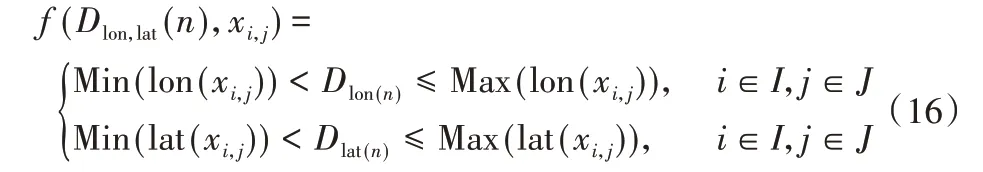
其中：Min（lon（xi，j））代表交通栅格网络xi，j位置的经度最小值；Max（lon（xi，j））代表交通栅格网络xi，j位置的经度最大值；Dlon（n）代表原始数据的经度；Min（lat（xi，j））代表交通栅格数据网络xi，j位置的纬度最小值；Max（lat（xi，j））代表交通栅格数据网络xi，j位置的纬度最大值；Dlat（n）代表原始数据的纬度。式（16）用来判别第n条记录的原始数据记录的车辆定位是否在xi，j网格中。

4.1.2 相关性分析

交通栅格数据生成后，以栅格数据x7，3为例，利用式（3）对其进行相关性分析，得到相关性曲线如图8 所示，图8（a）中得到与预测时间节点相邻14 天的相关性变化趋势，其中相邻一天的相关性最高，因此将相邻一天的交通栅格数据作为周期序列模型的输入。图8（b）中得到与预测时间节点相邻一天内的相关性变化情况，与其相邻的时间节点相关性较高，因此将相邻的3 个时间间隔作为邻近序列模型的输入。

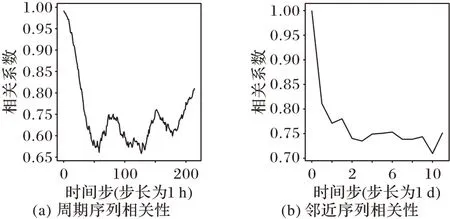
图8 交通栅格数据的相关性分析Fig.8 Correlation analysis of traffic grid data

4.1.3 评价指标

使用均方根误差（Root Mean Square Error，RMSE）和平均绝对误差（Mean Absolute Error，MAE）来测试模型训练效果，两者公式为：

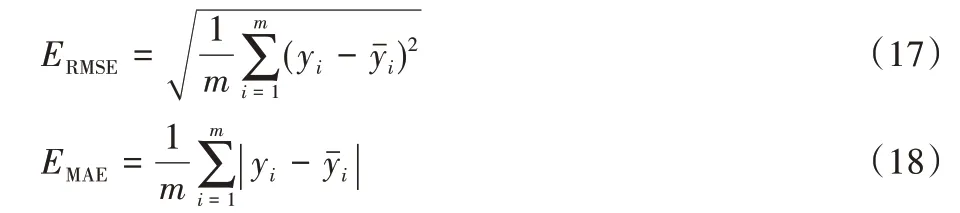
其中：yi为交通流数据真实值，为模型预测的交通流数据，m为样本数量。

4.2 模型参数设置

实验基于深度学习框架Pytorch-GPU 开发，使用Adam 优化器对模型进行优化，设置训练步长为0.000 01，BATCH_SIZE为每次训练样本数，设置为20，迭代次数设置为800，模型结构其他参数如表2 所示。

表2 改进时空残差卷积神经网络模型结构参数Tab.2 Structural parameters of improved spatio-temporal residual convolutional neural network model

4.3 结果分析

4.3.1 预测结果可视化

模型参数设置完成后，利用训练集对模型进行训练，将数据输入模型前，需要对数据进行标准化处理，降低不同量纲的影响，采用式（19）进行计算：

其中：xreal为交通栅格数据中一个时间段数据，μ(X)为交通栅格全体数据的平均值，σ(X)为交通栅格总体数据的标准差。

将标准化后的数据输入模型进行训练，利用测试集对模型进行训练，图9 展示了栅格网络x7，3在2014 年8 月26 日中的交通流真实值和预测值对比，可以看到，该模型能较好地挖掘交通流的时间特性。图10（a）展示了成都市在某一时刻的整体车流量情况，图10（b）为预测出的交通栅格图，模型能较好地挖掘城市网络的空间特性。

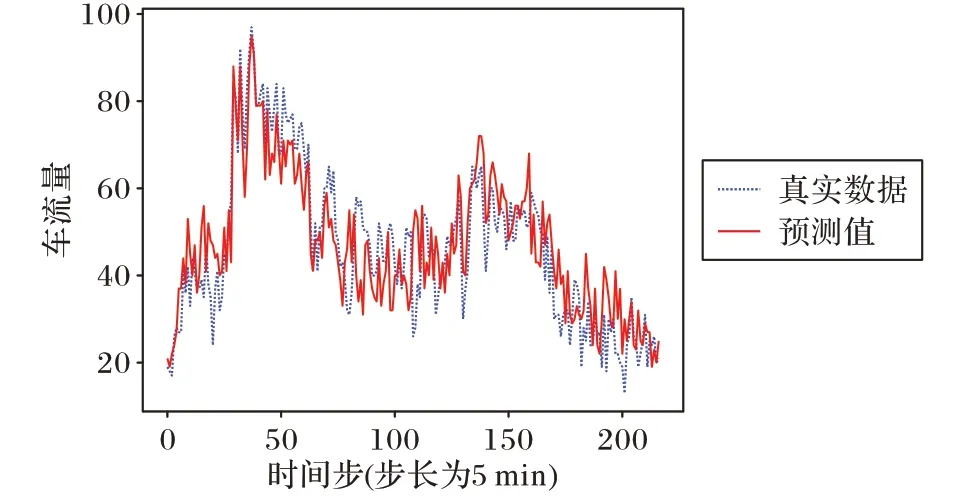
图9 2014年8月26日x7，3 路口车流量真实值与预测值对比Fig.9 Comparison of real and predicted traffic flow values at intersection x7，3 on August 26，2014

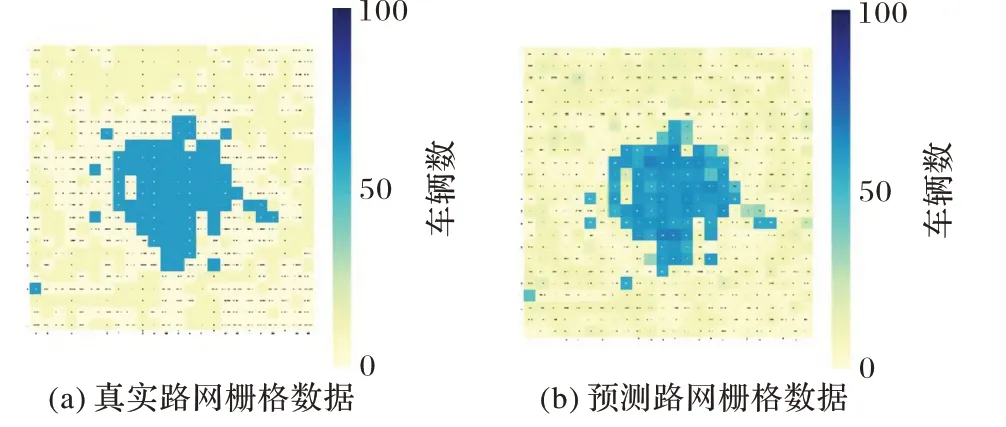
图10 城市路网车流量真实值与预测值Fig.10 Real value and predicted value of traffic flow in urban road network

4.3.2 性能对比

为验证模型的优越性，选取LSTM、CNN、ST-ResNet 作为基准模型进行模型对比。每个基准模型参数设置都与本文模型参数设置对标。为了测试每个模型的性能，使用基准模型和本文改进的模型对路网的数据进行预测，使用测试集7 d 的路网数据作为模型输入，利用均方根误差（RMSE）和平均绝对误差（MAE）比较模型输出结果，得到模型平均测试结果如表3 所示。

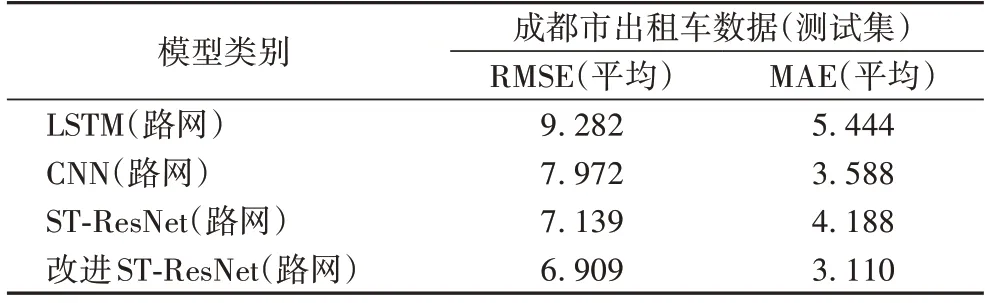
表3 模型性能比较结果Tab.3 Model performance comparison results

根据表3 实验结果发现，本文模型综合预测性能最优；LSTM 是基于时间序列的预测模型，对于交通流时空特性中的空间特性捕获能力较弱；CNN 作为传统的挖掘空间特性的预测模型，难以捕捉交通流中的时间特性；传统残差模型在处理城市路网交通流时，没有对时间序列进行筛选，容易捕获相关度低的时间序列，并且残差方法在捕获变化微小特征时，容易忽略长期时间特征等问题。

图11 给出了不同模型对测试集中一天路口交通流数据的拟合情况。

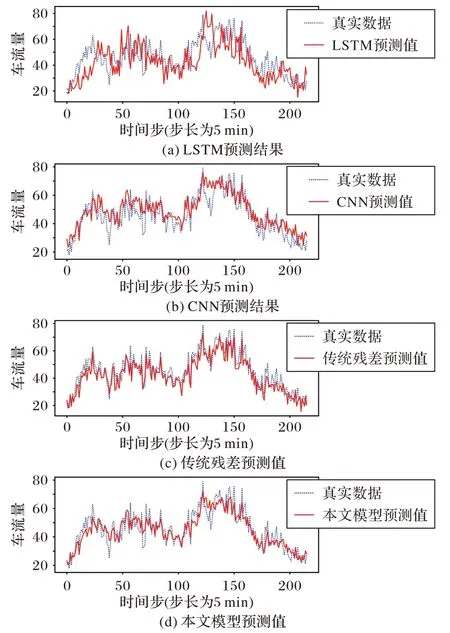
图11 模型预测数据拟合对比Fig.11 Comparison of model prediction data fitting

图12 为传统残差模型和本文模型针对城市路网的预测对比图，可以发现传统的时空残差模型在面对复杂交通网络时，可以较好地捕捉空间特征，但是时间特征捕获能力相对较差。

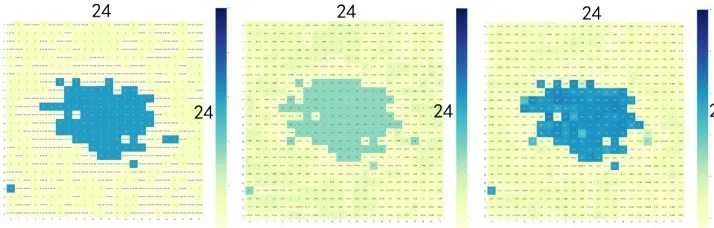
图12 本文模型与传统残差模型预测效果对比Fig.12 Prediction effect comparison between the proposed model and traditional residual model

图13 给出了改进时空残差卷积模型测试集7 d 的RMSE和MAE 比较结果。综合实验结果可知，本文模型在预测城市路网数据中相比其他模型具有较高的准确性。

图13 测试集上RMSE和MAE比较结果Fig.13 RMSE and MAE comparison results on test set

5 结语

针对城市路网交通流预测受到时空相关性的影响问题，本文提出一种基于改进时空残差卷积神经网络的城市路网短时交通流预测模型，对交通栅格数据进行皮尔逊相关系数分析，确定相关性高的周期序列和邻近序列，提高了模型输入数据的关联性；建立周期序列模型和邻近序列模型分别对两种序列数据进行处理，引入LSTM 神经网络作为混合模型提取时间特征，实现了对周期性和邻近性的长期时间特征的捕获。采用成都市出租车数据验证模型预测效果，结果显示该模型预测精度优于其他基准模型，表明考虑交通流相关性的时空混合模型对城市路网交通流预测是一个较好的尝试。下一步将重点对模型结构固化问题进行研究，使模型在复杂城市路网下具有较强的适应能力。