基于高阶位平面冗余的可逆信息隐藏方法

顼 聪，王兴田，陶永鹏

（1.大连外国语大学软件学院，辽宁大连 116044；2.大连外国语大学语言智能研究中心，辽宁大连 116044）

0 引言

可逆信息隐藏（Reversible Data Hiding，RDH）是在载体图像中可逆地隐藏附加数据，并能无差错地提取附加数据和无损恢复原始图像［1-2］。传统的RDH 主要有3 种方法：基于无损压缩的可逆信息隐藏算法［3-4］、基于直方图平移的可逆信息隐藏算法［5］和基于预测误差扩展的可逆信息隐藏算法［6-7］。随着网络的快速发展以及人们隐私意识的增强，加密图像的可逆信息隐藏（RDH in Encrypted Image，RDHEI）成为研究的热点。RDHEI 可以在不知道原始内容的情况下嵌入数据，实现了隐私、版权保护，可广泛用于军事、医疗等领域。例如：医学图像常被用作诊断依据，在医生和医生、医生和患者之间通过互联网进行传输和存储，通常此类图像中包含大量的个人隐私信息及有关医生的诊断说明信息。因此保护医学图像的信息安全极其重要。利用加密图像信息隐藏算法，通过对图像及嵌入信息的处理，一方面可以满足大量信息的嵌入，另一方面保证图像及嵌入信息在传输中不被识别和泄露。在接收端则可根据不同应用需要获取图像信息（如医学影像本身）及嵌入信息（患者的个人信息及诊断信息）。

根据加密前是否需要对图像进行预处理，现有的RDHEI算法可分为加密前预留空间（Reserving Room Before Encryption，RRBE）和加密后腾出空间（Vacating Room After Encryption，VRAE）两类。Zhang［8］提出基于VRAE 的位翻转RDHEI 算法。该算法按位异或加密原始图像，翻转加密图像块一半像素的三个最低有效位（Least Significant Bit，LSB）实现1 bit 数据的嵌入，算法的嵌入量较低。王子驰等［9］提出根据信息隐藏密钥在每个加密图像块中随机地选取多个集合，修改每个集合嵌入比特数据以提高信息的嵌入容量。Li等［10］提出以单个像素为单位进行比特位的翻转嵌入信息，同时采取随机扩散策略在多个像素中隐藏相同的信息，该算法有效地提高了信息的嵌入量。Qin 等［11］提出将加密的图像块分为平滑块和复杂块，通过压缩平滑块的最低有效位（LSB）获得信息嵌入空间。李志佳等［12］提出使用同态加密算法加密原始图像，对加密的图像分块，建立分块差值直方图，选取峰值点嵌入机密信息。该算法实现了密文域可逆信息隐藏，同时提高了信息的嵌入容量，但是同态加密计算增加了算法的复杂度。VRAE 类算法总体上是将数据嵌入到加密像素指定的后几位比特位中，能够获得较好的解密图像质量，但信息的嵌入量有待提高。RRBE 类算法则是在加密前预留嵌入空间进行机密信息嵌入。Ma 等［13］提出在图像加密前使用传统的RDH方法预留嵌入空间，图像加密后进行信息嵌入，其算法的最大嵌入率（Maximum Embedding Rate，MER）仅为0.5 bpp。Chen等［14］提出利用重排方式将较高阶位平面的相关比特位聚类，生成相应的重排比特流，利用扩展游程编码压缩比特流腾出嵌入空间，以位替换方式进行信息嵌入；但是扩展游程编码并不能提供令人满意的压缩率。Yi 等［15］提出根据图像块位平面0 或1 比特位的分布，将图像块划分为好块或坏块，压缩好块的位平面生成嵌入空间。该算法虽然在一定程度上能够提高信息的嵌入量，但是嵌入量的大小容易受到图像位平面0或1 比特位分布的影响，而且为了图像的可逆恢复，存储了过多的附属信息，使得直接解密后图像的峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）值较低。Li等［16］提出在图像加密前利用像素的预测误差扩展预留嵌入空间，修改加密后图像的预测差值直方图进行信息嵌入。该算法由于直方图峰值间的差值没有被加密，因此存在一定安全隐患，另外由于峰值点及其附近像素的大量改动使得直接解密后图像的PSNR 较低。此外，RRBE 类算法的实现需要图像所有者预处理图像，对图像所有者有较高的要求。

综上，目前常用的RDHEI 算法嵌入容量不高的主要原因是：加密后图像像素没有足够的冗余空间，并且由于图像可逆恢复的要求引入了过多的附属参数以及对图像进行过多的修改，使得解密后的图像PSNR 值降低。基于此，本文提出一个新的RDHEI 方法。首先，对图像分块，并以块为单位加密原始图像，保留块中大部分像素高阶比特位的相关性；然后，利用同块内像素的高阶位平面冗余，将对应的低阶位平面数据嵌入其中，在低阶位平面中腾出大量的可嵌空间。实验结果表明该方法可以获得较大的信息嵌入空间，提高了信息的嵌入率，直接解密的标记图像也有很好的视觉质量。

1 本文方法框架结构

本文方法包括三个主要阶段，即图像加密、机密信息嵌入，以及信息提取和图像恢复，图1 给出了该方法的框架。首先，原始图像I被分成不重叠的块，通过加密密钥Key1 产生Logistic 映射的混沌序列对图像子块内的像素进行异或加密；然后，使用加密密钥Key2 完成对图像块的位置置乱生成加密图像，保留了图像分块中像素的高阶比特位的相关性，使得图像块的高阶位平面中存在较大的冗余空间。在机密信息嵌入过程中，加密的图像块依据规则划分成可嵌入块、不可嵌入块和辅助块三种。在可嵌入块中，将高阶位平面的冗余转移到低阶位平面中，在低阶位平面中生成可嵌空间，嵌入加密的机密信息，生成标记的加密图像，同时将必要的附属参数存入辅助块中。接收方接收到标记的加密图像，通过辅助块的信息，仅使用数据隐藏密钥Kh可提取嵌入的机密数据；仅使用加密密钥可以直接得到在视觉上类似于I的解密图像；同时使用加密密钥和隐藏密钥时，可以成功提取嵌入的信息，并无损恢复原始图像。

图1 本文方法框架Fig.1 Framework of the proposed method

2 图像加密

Logistic 映射是1976 年数学生态学家梅（R.May）提出的具有重要意义的非线性迭代方程，是用于研究混沌系统经典模型，常用于信息安全领域的研究［17］。Logistic 映射的计算式为：

其中u是系统的控制参数，u取不同值时，式（1）会显示不同的状态：当3.569 ≤u≤4，系统处于混沌状态。本文用控制参数u和初始值x0作为加密密钥Key1。

原始图像I被划分成不重叠的块，设图像大小为H×W，分块大小为s×s，则一共有K个图像块，其中。对于能够完整块划分的图像即mod(H，s)=0且mod(W，s)=0，其中mod 是取模运算。按照光栅顺序从上到下、从左到右标记图像块和块内像素的序列号，令Bi为第i个图像块，则1 ≤i≤K；令Pi，j为Bi块内的第j个像素，则1 ≤j≤M，M=s×s。通过Logistic 的混沌映射生成具有K个随机数的混沌序列，将每个随机数和图像子块中的像素进行异或加密。具体方法如下：迭代式（1）K次，生成随机数组A，根据式（2）将A数组元素映射成序列F。

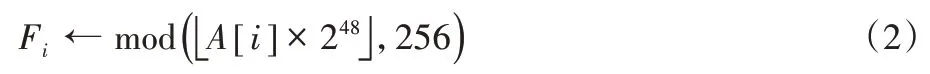
其中：A［i］是数组A的第i个元素，Fi是F序列的第i个元素。由于要保留加密域中每个块内邻近像素的空间相关性，所以使用Fi来加密第i个图像块Bi的每个像素，计算式如下：

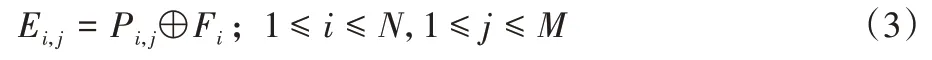
其中：Ei，j是加密后的像素，符号“⊕”代表按位XOR。

为了进一步提高图像的安全性，接着进行块置乱操作。设置加密密钥Key2 为随机种子，生成1 到K的不重复的随机自然数序列G，根据序列G将块的位置置乱，得到新的块序列为{BG1，BG2，…，BGk}，合成加密图像Ie。

对于不能完整块划分的图像即：mod(H，s)！=0或mod(W，s)！=0。首先按照从上至下、从左到右统计不能进行块划分的行列像素，设个数为L。这些像素只进行异或加密，不做位置置乱和信息嵌入处理，然后对剩余行列像素进行完整图像块划分。首先利用式（1）、（2）生成具有L+K个随机数的序列，前L个随机数和不能进行块划分的行列像素依次进行异或加密，后K个随机数按照前文描述方法进行块加密，接着利用加密密钥Key2 完成块置乱，最后合成加密图像Ie。

3 数据嵌入

在加密图像块中，保留了像素的相关性，块内的高阶位平面中含有较多的冗余空间，利用这些冗余空间嵌入机密信息。

3.1 图像分块

数据隐藏方接收到加密图像Ie之后，首先将该图像划分成不重叠的加密图像块Ci（1 ≤i≤K），大小为s×s（与加密时的块大小保持一致）。根据3.2 节中的算法，图像像素的冗余被保存在Ie中类型为Ca的可嵌入块中，因此可以在这些块中进行信息嵌入。

3.2 高阶位平面冗余空间转移

图像分块后，冗余部分会出现在部分块的高阶位平面。为了判别图像块是否可嵌，首先将每个图像块内的像素表示为Xi，j（i表示该像素属于图像块Ci，j表示该像素为图像块中的第j个像素）；接着将像素Xi，j分成高阶位部分、中阶位部分和低阶位三部分，计算式如下：

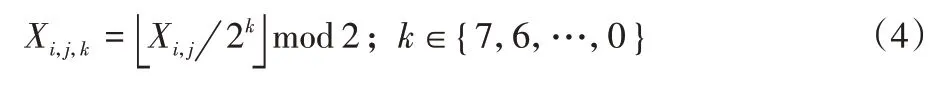
获取像素Xi，j的第k位比特值，值为0 或1。

大量实验证明高阶位值不宜超过3，超过3 后会显著减少可嵌入块的数量。依次计算块中的每个像素的高阶位部分、中阶位部分和低阶位部分，当块内所有像素的高阶位部分相同，则说明该块具有较高冗余，可以进行信息嵌入，标记为Ca块；否则该块不可用于信息嵌入，标记为Cb块。对于图像中的Ca块，根据式（6）可知像素的高阶位部分和低阶位部分个数相同，因此用像素低阶位部分替换对应的高阶位部分，并将低阶位部分置0。该方法本质上是将块内像素高阶位平面的冗余转移到对应的低阶位平面上，从而在低阶位平面上腾出嵌入空间。像素完成高阶位冗余转移后，计算式如下：

合成的可嵌入像素计算式如下：

为了图像的可逆恢复，块内第一个像素的高阶位部分保持不变，用来恢复整个图像块中所有像素的高阶位部分。块内所有像素低阶位平面则用于信息嵌入。加密图像的最大嵌入率（Maximum Embedding Rate，MER）计算式如下：

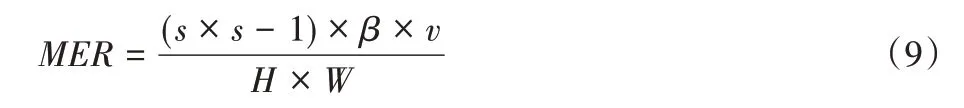
其中v为图像可嵌入块个数。

对于图像中的不可嵌入块Cb，在数据的嵌入过程中则保持不变，以减少对图像的改动，保证直接解密后的图像视觉质量。加密图像的块类型划分如表1 所示。

表1 加密图像块的类型Tab.1 Types of encrypted image blocks

3.3 附属参数的存储

为了信息的提取和图像恢复，需要存储必要的附属参数信息，包括位图MP、分块大小s和分块像素的高阶位个数α。

加密图像块分为Ca和Cb两类，Ca块用于信息嵌入，Cb块保持不变，因此需要用位图记录各类型块的位置。首先通过光栅扫描所有的图像块，如果为Ca块，则在位图对应位置1，否则置0，如图2 所示。

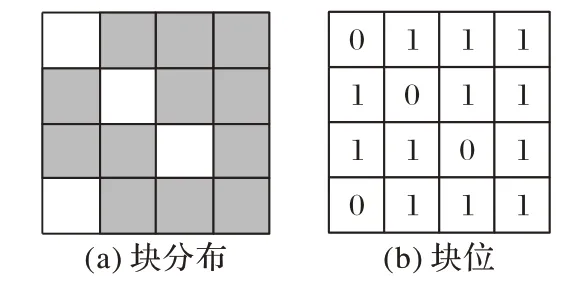
图2 类型块的分布图及相应的位图Fig.2 Type block distribution map and corresponding bitmap

图2（a）表示图像中可嵌入块和不可嵌入块的分布；图2（b）表示对应的位图，其中1 表示对应位是可嵌入块，0 表示对应位是不可嵌入块。由于加密图像块高阶位平面冗余空间的存在，位图表现出稀疏性，通过压缩位图可以显著减小存储附属参数信息所用的存储空间。位图包含很少的0 元素，因此可以通过存储0 元素的位置和个数信息来压缩整个位图。设e1和e0分别代表位图中1 元素和0 元素的个数，由于e0＜e1，存储0元素个数需用到的位数，计算式如下：

使用元组（行，列）记录少数像素位置，存储0 元素的位置信息需用到的位数，计算式如下：

通过计算相邻0 元素的位置差值可以进一步减小Llco，设e0项的位置如下：

第i个少数元素的编码长度减小为：

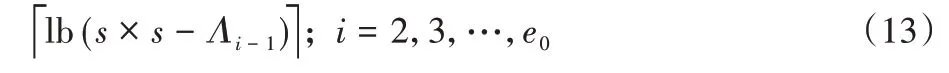
压缩后的Llco计算式如下：

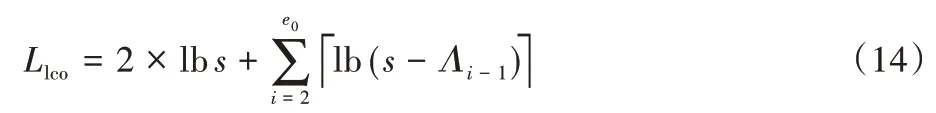
由于所有图像块的第一个像素在整个嵌入过程中保持不变，因此可以将压缩的位图信息的每一位按光栅顺序存储到每个图像块的第一个像素的最低有效位（LSB），被替换的LSB 形成位流sq，连接在加密的机密信息前。存储分块大小s的值需用4 个比特位，通过位替换方式存储在最后一个像素的低4 位；存储高阶位个数α的值需要用3 个比特位，同样方式存储在倒数第二个像素的低3 位值；分块大小最大值设为16，因此存储位图中可嵌入块个数的值需用16 个比特位，同样方式存储在倒数第三和第四个像素中。含有最后四个像素的图像块标记为块Cf，用于图像恢复。被替换下的原像素比特位形成位流st，将连接在位流sq前。st、sq连同加密数据共同存入可嵌入块的冗余空间中。

4 信息抽取和图像恢复

在加密图像信息隐藏算法中，通常密钥只有几十比特，数据量很小，因此通信双方可以事先协商利用特定安全通道进行传输。根据图像的不同处理要求，在特定通道中传输指定的密钥，使得接收方拥有不同的密钥类型和对应的权限。当接收方既拥有数据隐藏密钥又拥有加密密钥时，可以提取出机密数据，并无损恢复原始图像；仅拥有数据隐藏密钥时，接收方则只能提取出嵌入的机密数据；仅拥有加密密钥时，接收方则可以获得轻微失真的原始图像。

4.1 只有隐藏密钥Kh，获取机密数据

接收方接收到加密的标记图像Iew后，按以下步骤获取机密信息：

1）获取标记图像Iew最后四个像素的23 位信息，计算图像分块大小s、位平面高阶位个数α，以及位图中可嵌入块的个数e0。

2）根据分块大小s对标记图像Iew分块，然后进行光栅扫描，根据可嵌入块的个数e0和式（13）、（14），从前Llco个块的第一个像素的LSB 中获取可嵌入块的位置信息，恢复位图MP，标出图像中Ca、Cb和Cf块。

3）依次连接所有可嵌入块的低阶位平面，从中依次分解出23 位的st流，Llco位的sq流，剩余部分则为嵌入的加密机密数据。

4）对获取的加密的机密数据用隐藏密钥Kh解密得到原始的机密信息。

4.2 只有加密密钥，解密获得近似的原始图像

接收方接收到加密的标记图像Iew。

1）获取标记图像Iew最后四个像素的位信息，计算图像分块大小s、位平面高阶位个数α，以及位图中可嵌入块的个数e0。

2）根据4.1 节中的方法，恢复位图MP，并标出图像中Ca和Cb及Cf块，并从所有可嵌入块的低阶位平面中分解出st流、sq流。

3）用st流替换Cf块中的最后4 个像素的比特位，用sq流替换前Llco个块的第一个像素的LSB 位。

4）用所有Ca块第一个像素的高阶位替换同块内其余像素的高阶位，恢复Ca块内像素的高阶位平面。

5）根据加密密钥Key2 恢复图像块的原始位置，根据Logistic 映射的加密密钥Key1 生成原图加密时的混沌序列，经过式（2）映射后，对块内像素解密，可得带有嵌入信息的解密图像。由于嵌入方只在Ca块高阶位平面冗余转移的低阶位平面中嵌入数据，高阶位平面得以完全恢复，Cb块不作嵌入数据，Cf块可以完全恢复，因此解密后获得的带嵌入信息的图像有近似原图的视觉效果。

4.3 使用Kh和加密密钥进行数据提取和图像恢复

接收方接收到加密的标记图像Iew。

1）获取标记图像Iew最后4 个像素位信息，计算图像分块大小s、位平面高阶位个数α，以及位图中可嵌入块的个数e0。

2）根据4.1 节中的方法，恢复位图MP，标出图像中Ca和Cb及Cf块，并从所有可嵌入块的低阶位平面中分解出st流、sq流和加密的机密数据。

3）根据4.1 节中的方法，利用Kh获取原始的机密数据；由于原Ca块中像素（第一个像素除外）高阶位是用同一像素对应低阶位替换的，所以用高阶位替换同一像素对应低阶位，并利用4.2 节中的方法恢复所有Ca块的高阶位，可以完全恢复Ca块。

4）根据4.2 节中的方法可以完全恢复Cb及Cf块，并使用加密密钥解密图像，可以完全恢复原始图像。

5 实验与结果分析

实验环境为：具有2.6 GHz Intel i5-4200U 处理器，4 GB的个人计算机内存，Windows 7 操作系统和Matlab R2016a。

5.1 安全性分析

通过香农熵和直方图进行加密图像的安全性分析。加密图像的熵的计算式如下：

其中：E是具有256 个灰度等级的灰度图像，而p(xi)是灰度等级xi（0 ≤i≤255）的概率。H(E)的最大理论值为8。熵越大，则表示加密的图像越安全。表2 给出了加密后的6 个标准灰度图像的熵，可以发现所有熵都非常接近最大理论值8，这说明加密图像是安全的。

表2 加密图像的熵Tab.2 Entropies of encrypted images

理论上高效的加密方法生成的加密图像，其直方图分布均匀，无法通过直方图的检测技术确定原始图像，从而保证加密图像的安全性。图3 给出了6 个标准图像加密后的直方图，可以看到这些直方图几乎是均匀分布的。

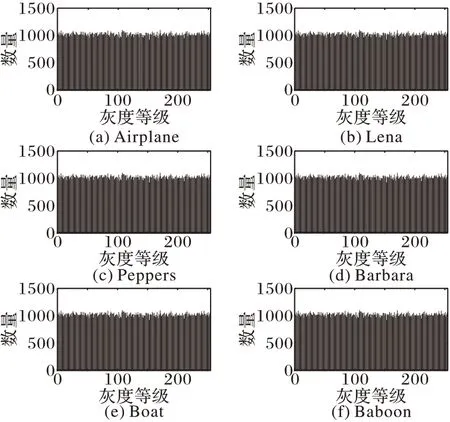
图3 加密图像的直方图Fig.3 Histograms of encrypted images

5.2 单个图像测试

设置块大小为4，高阶平面数为3，对标准灰度图像Peppers 进行单体测试，各项测试指标的结果如图4 所示。图4（a）表示原始图像；图4（b）表示不带任何数据的加密图像；图4（c）是嵌入的加密图像，其最大嵌入率计算为1.79 bpp；图4（d）表示直接解密的标记图像，通过加密密钥，可以获得容量为1.79 bpp 的解密图像，视觉上与原始图像I几乎相同（PSNR=46.87 dB）；图4（e）表示恢复的图像，其PSNR 值为无穷大，完全恢复。

图4 单个图像的测试结果Fig.4 Single image test results

5.3 不同参数设置对算法的影响

不同的分块大小和高阶位个数会直接影响到可嵌入块的数量及块内像素的高阶位平面冗余，从而影响图像的可嵌入容量和直接解密后的图像视觉质量。

选择不同纹理的6 个标准灰度图像对算法进行测试。测试中，图像块的大小分别设置为2×2、4×4、6×6 和8×8，依次将图像块的高阶平面数设置为1、2、3。实验结果如表3 所示，使用MER 和直接解密标记图像的PSNR 作为评估算法的指标。

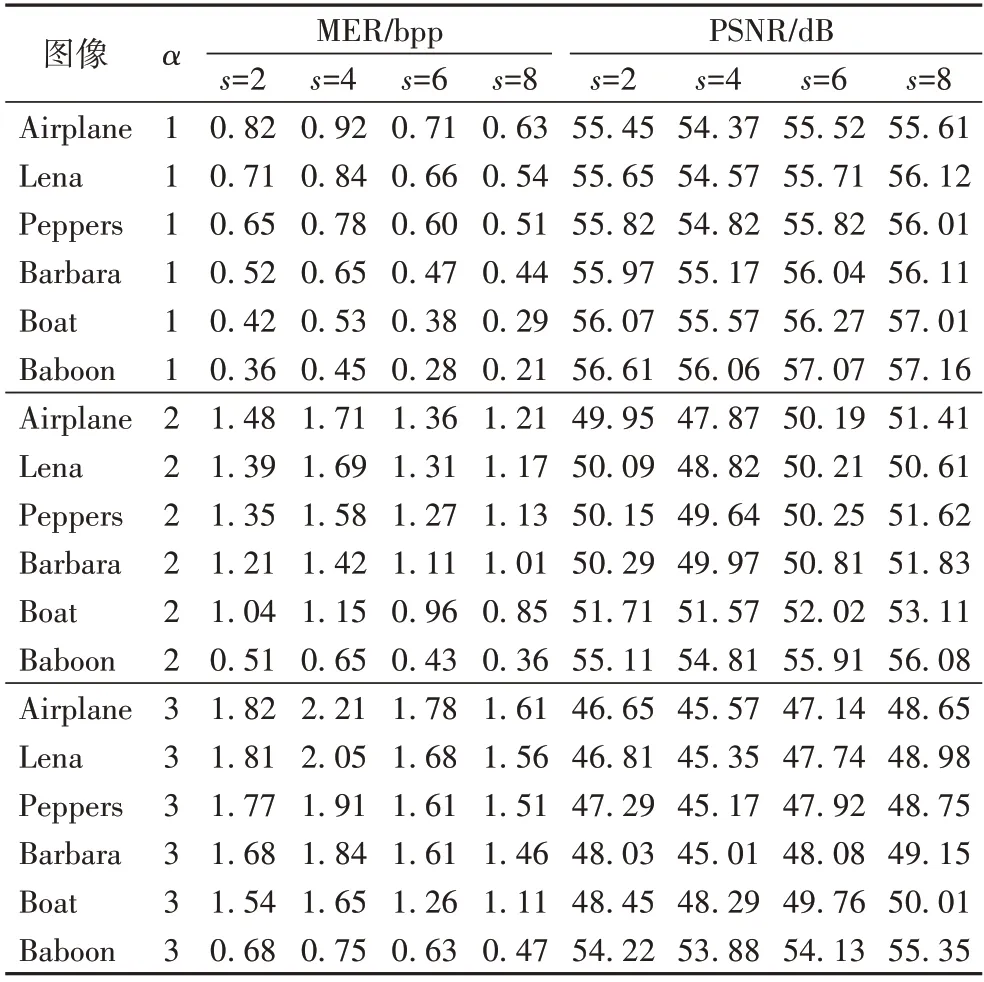
表3 在不同高阶平面数α和不同分块大小s下图像的MER和PSNR值Tab.3 Image MER and PSNR values under different high-order bit-plane numbers α and different block sizes s

表3 结果表明，随着图像纹理复杂度增强，相同参数条件下图像的最大嵌入率降低。这是因为随着图像纹理增强，可嵌入块的个数减少，使得嵌入容量降低。

对单个图像来说，给定高阶位平面个数α，则图像分块s越大，最大嵌入率MER 就越高，直接解密的标记图像PSNR值越小。这是因为较大的分块大小s可将更多机密信息嵌入到单个可嵌入块中，同时减小了附属参数信息的大小；另一方面，嵌入更多机密信息将改动更多的图像部分，使得解密后标记图像的PSNR 值减小。但是需要注意的是，当s增大超过4 时，块内像素的相关性减弱，具有相同高阶位个数α的像素个数减少，从而可嵌入块的数量降低，最大嵌入率MER 降低，解密后标记图像的PSNR 值升高。

对于给定分块大小s，随着高阶平面个数α的增大，大多数测试图像的最大嵌入率MER 逐渐升高，直接解密图像的PSNR 值逐渐降低，这是因为随着α的增大，一方面是可嵌入块中的可嵌入比特位数增加，另一方面可嵌入块的数量减少。当α小于3 时，大多数测试图像的MER 都会逐渐增加。当α等于3 时，在大多数测试图像中这两方面的作用达到平衡，这些图像的MER 达到最大值，而此时PSNR 并没有太显著降低。

5.4 不同算法的比较

为了验证本文算法的优越性能，将其和文献［14-16］算法进行比较，所有算法的参数均为最优性能下的指标值。本文算法α=3，s=4。各个算法的嵌入率和直接解密图像的PSNR 值的关系曲线如图5 所示。

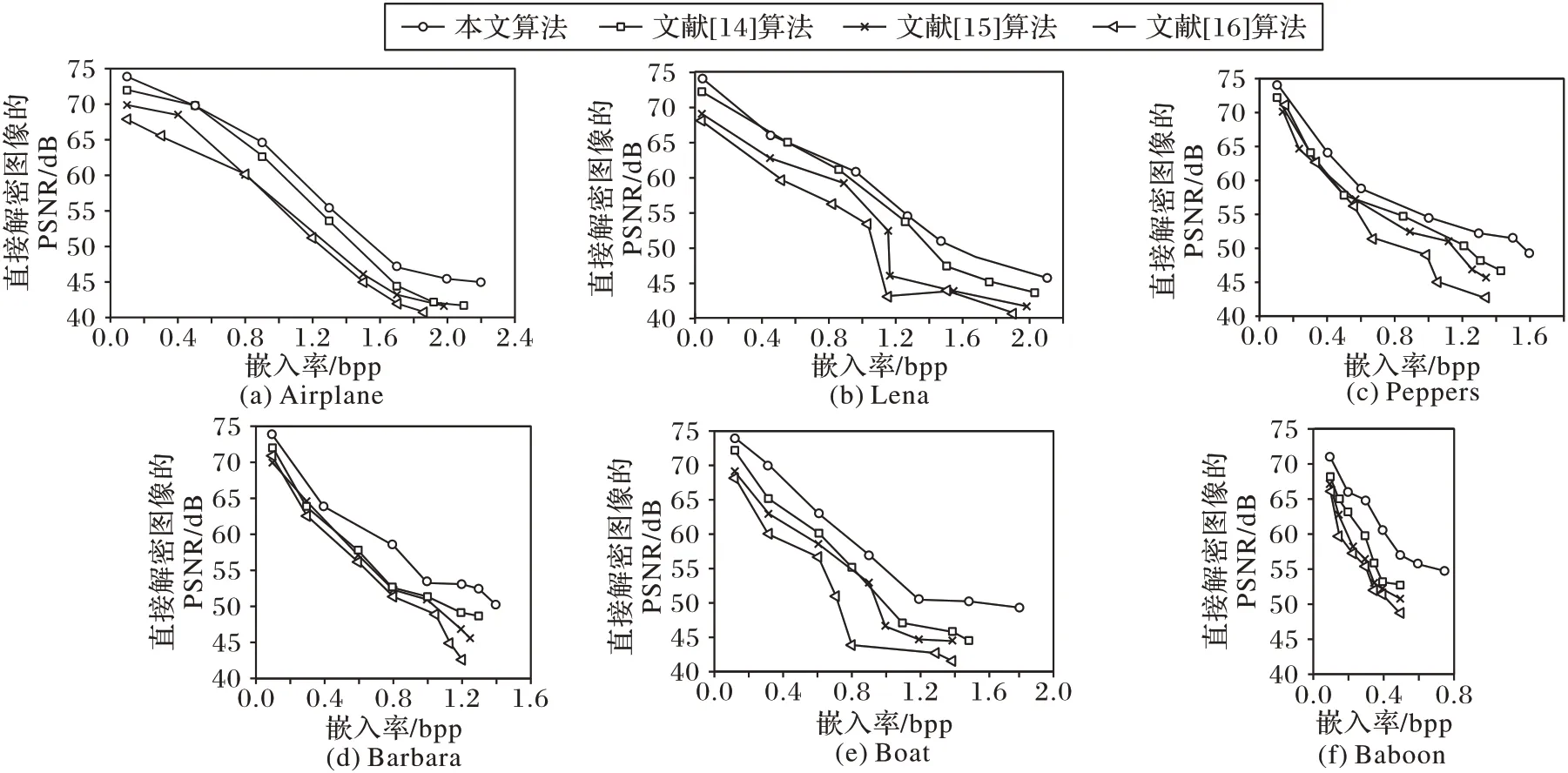
图5 不同算法的对比测试结果Fig.5 Comparison test results of different algorithms

图5 展示了各个算法在有效负载下标记的解密图像的PSNR 值的比较曲线。从图5 中可以看到，本文算法的最大嵌入率大于所有比较方法，而且在较平滑的图像Airplane、Lena 上最大嵌入率超过2.0 bpp。这主要是因为本文算法利用了更多高阶位平面的冗余从而增大了嵌入量。Chen 等［14］通过重排高位平面比特位的方式也获得了较高的嵌入量。而Yi 等［15］将图像分为5 种类型块的压缩方法，由于附属参数信息占用空间较多，影响了信息的嵌入率，从而性能低于本文算法。Li 等［16］利用多轮预测误差扩展来嵌入数据，相较于多平面压缩的方式嵌入量要小得多。另外可以看到，在嵌入率相同的情况下本文算法的PSNR 值也高于文献［14-16］中算法。这是因为本文算法在最优参数条件下，嵌入量和解密标记图像的PSNR 取得平衡；另外是在可嵌入块的低阶位平面中嵌入机密数据，其余部分则保持不变，所以在保证嵌入量的同时具有较好的直接解密图像的PSNR 值。

6 结语

针对目前RDHEI 算法无法更有效地从加密图像中获得更多嵌入空间的问题，本文提出一种基于高阶位平面冗余的可逆信息隐藏方法。在本文方法中，一方面实现了较大的信息嵌入量；另一方面，即使传输过程中图像遭到非法攻击、非法篡改的情况，图像及嵌入信息的安全性仍然能得到保证，即原始图像不能被识别，嵌入信息不会被泄露。这一点有其广泛的应用价值，如在医学、军事领域，首先需要保证的是图像及嵌入信息的安全性，信息即使被破坏也不能被泄露；其次在医学、军事领域需要在图像中嵌入大量的信息。本文方法都可以满足条件，另外在复原信息位没有被篡改的情况下，接收方根据权限密钥仍然可以获得自己需要的信息。未来在信息防篡改及篡改信息恢复方面可进行进一步的研究，以更好地提高图像的安全性。