基于Hessian正则化和非负约束的低秩表示子空间聚类算法

范莉莉，卢桂馥，唐肝翌，杨 丹

（安徽工程大学计算机与信息学院，安徽芜湖 241000）

0 引言

在信息社会高速发展的今天，高维数据越来越多，结构越来越复杂，如何进行高维数据聚类分析已成为亟须解决的难题。人们通常假设高维数据分布于一个联合的低维子空间中，这一合理假设推动了子空间聚类算法的发展。目前，子空间聚类［1-4］已成为解决高维数据聚类的一种重要方法，广泛应用于计算机视觉、模式识别和机器学习等相关领域的研究中。

子空间聚类的思想［5］是将来自多个线性子空间的一组高维数据，根据类别的不同分割到相互独立的子空间中。常用的子空间聚类算法主要有：迭代方法、代数方法、统计方法和基于谱聚类的方法。基于谱聚类的方法［6-7］因在算法效率和聚类精度上的较好效果，是目前子空间聚类算法的重点研究方向。该方法主要利用数据点周围的局部信息或全局信息的相似性构造亲和矩阵，然后运用谱聚类方法得到聚类结果。数据点间的最优表示直接影响后面的聚类效果。

稀疏子空间聚类（Sparse Subspace Clustering，SSC）算法［8］和低秩表示（Low-Rank Representation，LRR）子空间聚类算法［9-10］是代表性的两种子空间聚类算法，它们通过基于稀疏和低秩表示来有效处理噪声和异常值。SSC 算法利用L1范数设置类间相似性为0、类内相似性为1 来保证矩阵的稀疏性，但因忽略数据间的关联性，使得系数矩阵表示过于稀疏，可能会降低聚类的准确性。LRR 算法解决了这一问题，其通过最小核范数寻求数据全局结构的低秩表示，并对含噪声和重大污染的数据有较好的鲁棒性。文献［11］提出的最小二乘回归（Least Squares Regression，LSR）子空间聚类算法在子空间独立的假设下，能获得矩阵的块对角结构，更好地保持数据的聚集性。

上述经典算法为子空间聚类的研究奠定了很好的基础，近年来，不断有新的改进方法被提出来以提高聚类效果。文献［12］利用矩阵的Forbenius 范数对系数矩阵进行约束，通过高效密集子空间聚类（Efficient Dense Subspace Clustering，EDSC）来有效处理噪声和异常值，提高聚类准确度。文献［13］使用具有对称约束的低秩表示（Low-Rank Representation with Symmetric Constraint，LRRSC）来解决子空间聚类问题，通过将对称约束集成到高维数据表示的低秩属性中，扩展了原始的低秩表示算法。文献［14］从原始数据的低维空间动态学习亲和矩阵，通过低秩稀疏子空间（Lowrank Sparse Subspace，LSS）聚类方法提高聚类性能。然而这些算法都忽略了数据间的局部相关性，不能很好地揭示局部数据间的关系。为此，研究者们采用流形学习的方法来保持原有数据的拓扑和几何结构，以体现数据的局部流形特征。

目前大多数基于流形学习的子空间聚类主要应用拉普拉斯正则化来提升算法性能。文献［15］通过拉普拉斯正则化LRR（Laplacian regularized LRR，LapLRR）来探索数据的全局和局部流形结构，利用流形正则化来增强LRR 的性能。文献［16］提出了一个广义拉普拉斯正则化低秩表示框架，利用图正则化不仅可以表示全局低维结构，而且可以捕获局部数据结构中的非线性几何信息。文献［17］将图正则化引入到LRR 中，提出的图正则化LRR（Low-Rank Representation with Graph Regularization，LRRGR）算法集成了流形学习和低秩表示，可以很好地利用样本的全局和局部结构信息，并对噪声具有较好的鲁棒性。文献［18］提出的图正则化最小二乘回归（Graph-regularized Least Squares Regression，GLSR）算法，通过使用最小二乘回归代替核范数来产生分组效应，同时利用流形约束来保留样本的局部几何结构。这些算法通过使用拉普拉斯正则项来对数据的局部相关性进行表示，都较好地提高了子空间聚类的性能。然而，已有研究［19-20］表明拉普拉斯正则化使得该项的极小解倾向于一个常数，不能很好地保持数据的局部拓扑结构，这也导致了拉普拉斯算子缺乏推测能力。与传统的拉普拉斯正则化相比，Hessian 正则化有良好的推测能力，它不依赖于常量函数，该项的极小化使得最优函数为流形上的线性函数，从而可以更好地利用数据的拓扑信息，因此Hessian 正则化往往比拉普拉斯正则化更适合维护数据的局部流形结构。此外，现有算法求得的系数矩阵往往有正有负，而负值往往没有实际的意义。

近几年，随着神经网络的迅猛发展，深度学习在图像处理领域显示出了其强大的优势。文献［21］利用深度神经网络，提出了一种深度嵌入式聚类（Deep Embedded Clustering，DEC）方法，通过特征学习在低维空间中迭代优化聚类目标。文献［22］在深度自动编码器的基础上提出了一种无监督的深度子空间聚类网络（Deep Subspace Clustering Networks，DSC-Nets），利用自表达层来学习亲和矩阵。文献［23］提出了一种有监督的深度学习方法来优化嵌入函数，降低时间复杂度。文献［24］对稀疏子空间进行深度扩展，提出了L1范数的深度子空间聚类（Deep Subspace Clustering with L1-norm，DSC-L1）方法，可同时满足亲和矩阵的稀疏性及神经网络的非线性特点。上述方法都利用深度网络有效降低了分类错误率，体现出了良好的性能。然而，这些深度模型结构复杂、参数众多（几百万甚至更多的参数），算法复杂度高。为了达到算法的最佳性能，需要不停地调参，所需时间很长，且其应用在中小规模数据集时容易产生过拟合，因而其往往更适合大规模数据集的数据处理。而本文提出的算法参数较少（三个参数），算法复杂度低，能比较容易地达到算法的最佳性能，实验结果表明，其在一些常见的数据集上可以得到较好的聚类效果。

基于以上问题，本文提出了一种基于Hessian 正则化和非负约束的低秩表示子空间聚类算法（Low-Rank Representation subspace clustering algorithm based on Hessian regularization and Non-negative constraint，LRR-HN）。在LRR-HN 中：1）考虑到系数矩阵中的负值往往没有实际意义，将非负约束引入低秩表示的目标函数，来保证系数矩阵的有效性；2）受流形学习的影响，考虑到Hessian 正则项在保持数据局部拓扑结构上的良好表现［25-26］，将Hessian 正则项作为惩罚函数加入到目标函数，来更好地保持数据间的局部几何结构。此外，通过利用自适应惩罚的线性交替方向法，本文还设计了一种求解LRR-HN 的有效算法。在一些实际数据库上的实验表明，LRR-HN 优于现有的一些算法，具有更好的聚类性能。

1 相关算法

1.1 LRR 算法

给定一个数据矩阵X，X的N个数据点来自d个线性独立子空间的并，子空间聚类的目标是求解子空间的数目d和它们的维数，并将数据点分割到对应的子空间中。

LRR 算法［10］的基本思想是将数据矩阵X表示成在字典矩阵A下的线性组合。最理想的情况为数据是干净的。最小化模型的秩函数为：

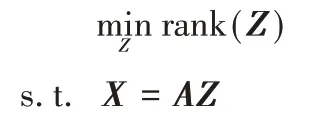
由于秩函数的优化问题是NP-hard，很难求解。一般的处理方法是用核函数来代替秩函数，最小化模型的核函数为：

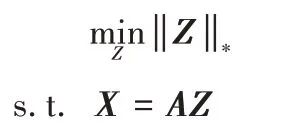
对于数据点有噪声的情形，加入噪声项E来增加鲁棒性，得到LRR 的基本模型为：

1.2 Hessian 能

设fk是将高维数据点xi映射为Vki的函数，即fk(xi)=Vki。设Np(xi)为数据xi的p个最近邻数据的集合，则fk在xi处的Hessian 可近似为：

2 Hessian 正则化的非负低秩表示

在本章中，针对LRR 算法数据局部相关性缺失及系数矩阵有正有负等问题，把非负约束和Hessian 正则项引入到目标函数（1），提出了基于Hessian 正则化和非负约束的低秩表示子空间聚类算法（LRR-HN）。

2.1 LRR-HN的目标函数

一般来说，从模型中获得的系数矩阵有正有负，但在实际应用场景中，系数矩阵中的负值可能是不合理且没有意义的。为了使系数矩阵更加合理和有意义，本文通过Z的非负约束，即Z≥0，保证每个数据点都位于其邻接点的凸包中，更能体现数据点之间的关联，使其在局部结构描述上更有意义。

另外，基于流形假设，即如果两个数据点在数据分布的本质几何结构中相近，那么这两个数据点在嵌入或投影到新的空间中也相近。因此为了保持数据局部拓扑结构，鉴于Hessian 能的良好性能，本文把Hessian 正则项=tr(VTMV)作为惩罚项融入低秩表示的目标函数（1）中，来更好地表达局部数据间的相关性。

将系数矩阵Z代入Hessian 正则项，则LRR-HN 的目标函数最终定义为：

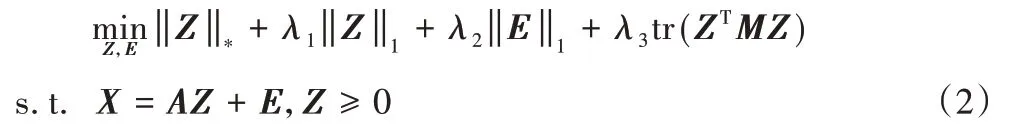
2.2 LRR-HN的求解算法

为求解问题（2），本文采用自适应惩罚的线性交替方向法（Linearized Alternating Direction Method with Adaptive Penalty，LADMAP）［27］求解。使用X作为字典并引入辅助变量C，将式（2）转化为

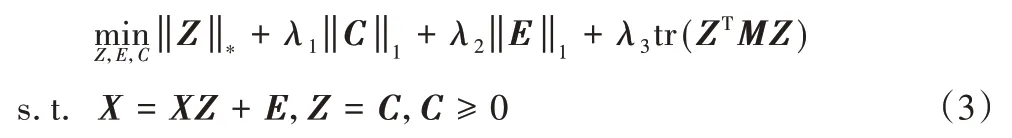
式（3）的增广拉格朗日函数为

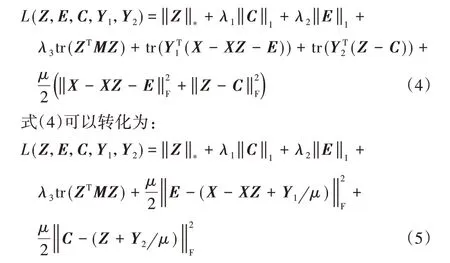
其中：μ＞0是惩罚参数，Y1、Y2为拉格朗日乘子。

固定C，E，更新Z：

式（6）没有闭合解。通过应用LADMAP［27］，本文将L1中的平滑部分表示为：

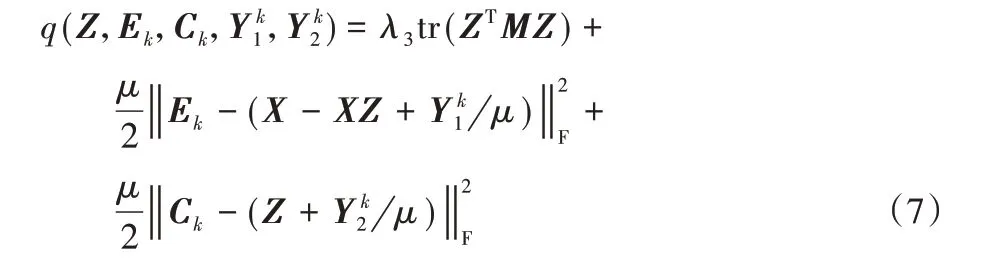
那么L1的最小化问题可替换为求解下列问题：

综上所述，LRR-HN的求解算法如算法1所示。

算法1 LRR-HN的求解算法。

2.3 基于LRR-HN的子空间聚类

通过求解式（2）得到系数矩阵Z*后，本文采用文献［17］的方法构造亲和矩阵，然后应用K-means 方法得到最终的聚类结果。基于LRR-HN 的子空间聚类算法如算法2 所示。

算法2 基于LRR-HN的子空间聚类算法。

2.4 收敛和复杂性分析

算法1 是LADMAP 的直接应用，可收敛到式（2）的全局最优解。有关LADMAP 的收敛证明，可详见文献［27］。

通过奇异值阈值更新Z时，本文可以使用文献［29］中提到的秩预测策略来预测Zk+1的秩r，然后对Z进行奇异值分解，取前r个奇异值及对应的向量。这使得奇异值分解的计算复杂度为O(rn2)，其中n为数据矩阵X的列数。但此时算法1 的复杂度仍为O(n3)，因为构造Zk是全尺度的矩阵乘法。采用文献［27］中的Lanczos 方法，只需要Zk的缩减矩阵乘法，其中Z=Zk-∇zq(Zk)/η1。这样处理后，算法1 的迭代复杂性为O(rn2)。

3 实验及结果分析

3.1 实验设置

3.1.1 实验所用的数据集

为了验证算法的有效性，分别在Yale 数据集和ORL 数据集上进行了实验。Yale 数据集由耶鲁大学创建，里面包含15 个人的165 幅灰度人脸图像。每个人在不同的表情、姿态、光照等条件下拍摄11 张照片。本实验中，图像的大小为32×32。图1 为用于实验的Yale 数据集中的部分图像。

图1 Yale数据集中的部分图像Fig.1 Some images in Yale dataset

ORL 数据集由剑桥大学创建，里面包含40 个人的面部图像。每个人在较暗的均匀背景下拍摄10 张照片，这些照片是在不同的时间、光照、面部表情和面部细节环境下采集的。本实验中，图像的大小为32×32。图2 为用于实验的ORL 数据集中的部分图像。

图2 ORL数据集中的部分图像Fig.2 Some images in ORL dataset

3.1.2 方法比较

实验中将本文算法分别与K均值（K-means）［30］、非负矩阵分解（Non-negative Matrix Factorization，NMF）［31］、主成分分析（Principal Component Analysis，PCA）［32］、归一化切割（Normalized cut，Ncut）［33］、LRR［10］和自适 应低秩表示（Adaptive Low-Rank Representation，ALRR）［4］等6 种具有代表性的算法进行比较，以验证本文所提算法的有效性。

K-means 是一种基于距离的聚类算法。其思想是随机选择几个类作为初始的聚类中心，根据每个样本与聚类中心的距离划分类别，更新聚类中心，重复以上过程，直到收敛为止。

NMF 是一种无监督学习算法。NMF 算法能够将一个任意给定的非负矩阵分解为左右两个非负矩阵的乘积，从而对数据进行降维。本文实验中将原始数据应用NMF 降维后采用K-means 进行聚类。

PCA 是一种常用的无监督数据降维方法。通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于特征提取及噪声去除。本文实验中将原始数据应用PCA 降维后采用K-means 进行聚类。

Ncut 是一种谱聚类方法。其通过邻接矩阵求解特征值及特征向量，将特征向量归一化后构造新的矩阵，然后应用K-means 进行聚类。

LRR 是一种低秩表示的子空间聚类算法，通过寻找数据在自身数据字典上的低秩表示来求解亲和矩阵，然后应用Ncut 方法进行聚类。

ALRR 是一种自适应低秩表示算法，可用于子空间聚类。其通过自适应字典学习策略获取投影矩阵和低秩表示，然后将Ncut 方法应用于亲和矩阵进行聚类。

3.1.3 评价准则

为评估所提出算法的性能，本文采用正确率（ACcuracy，AC）和归一化互信息（Normalized Mutual Information，NMI）两种评价准则［34］来对算法性能进行定量评价。

设xi为数据样本，gi为样本xi的真实类别，为样本xi聚类求出的类别，则AC 方法定义为：

其中：n为样本总数，δ(a，b)为delta 函数，当且仅当a=b时，δ(a，b)=1；否则，δ(a，b)=0。

设两种聚类结果为D和D′，则NMI方法定义为：

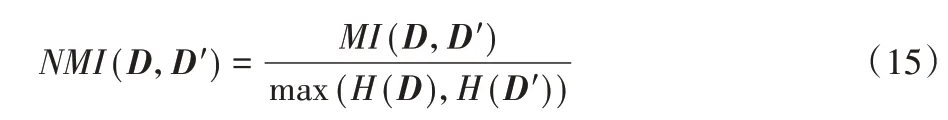
其中：H(D)和H(D′)表示聚类D和D′的熵，MI(D，D′)表示D和D′的互信息。

本文算法中主要涉及3 个参数，分别是平衡参数λ1、λ2和λ3。在本次实验中将会分析3 个参数在不同数据集中对AC 和NMI 两个评价准则的影响。本文的实验环境为Microsoft Windows 10，处理器为英特尔酷睿i5，内存容量16 GB，所有算法采用Matlab 2016a 编程实现。

3.2 聚类结果分析

Yale数据集中包含15个人，每人11张照片。为了更好地比较不同算法上的聚类结果，分别选用前m（5、8、12、15）个类别相关数据进行聚类。不同算法在Yale 数据集上的聚类结果如表1所示。

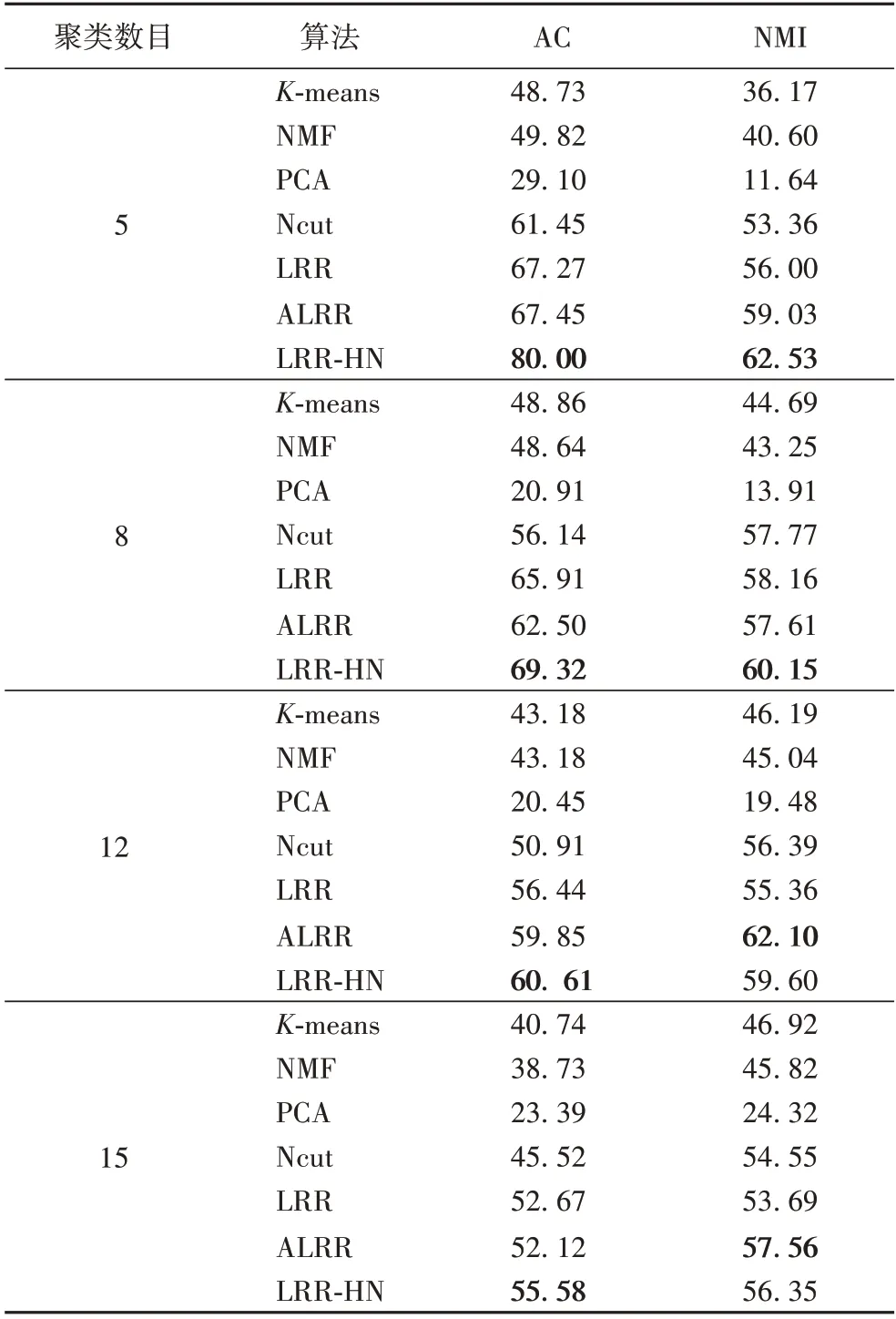
表1 不同算法在Yale数据集上的聚类结果 单位：%Tab.1 Clustering results of different algorithms on Yale dataset unit：%

ORL数据集中包含40个人，每人10张照片。分别选用前m（10、20、30、40）个类别相关数据进行聚类，不同算法在ORL数据集上的聚类结果如表2所示。

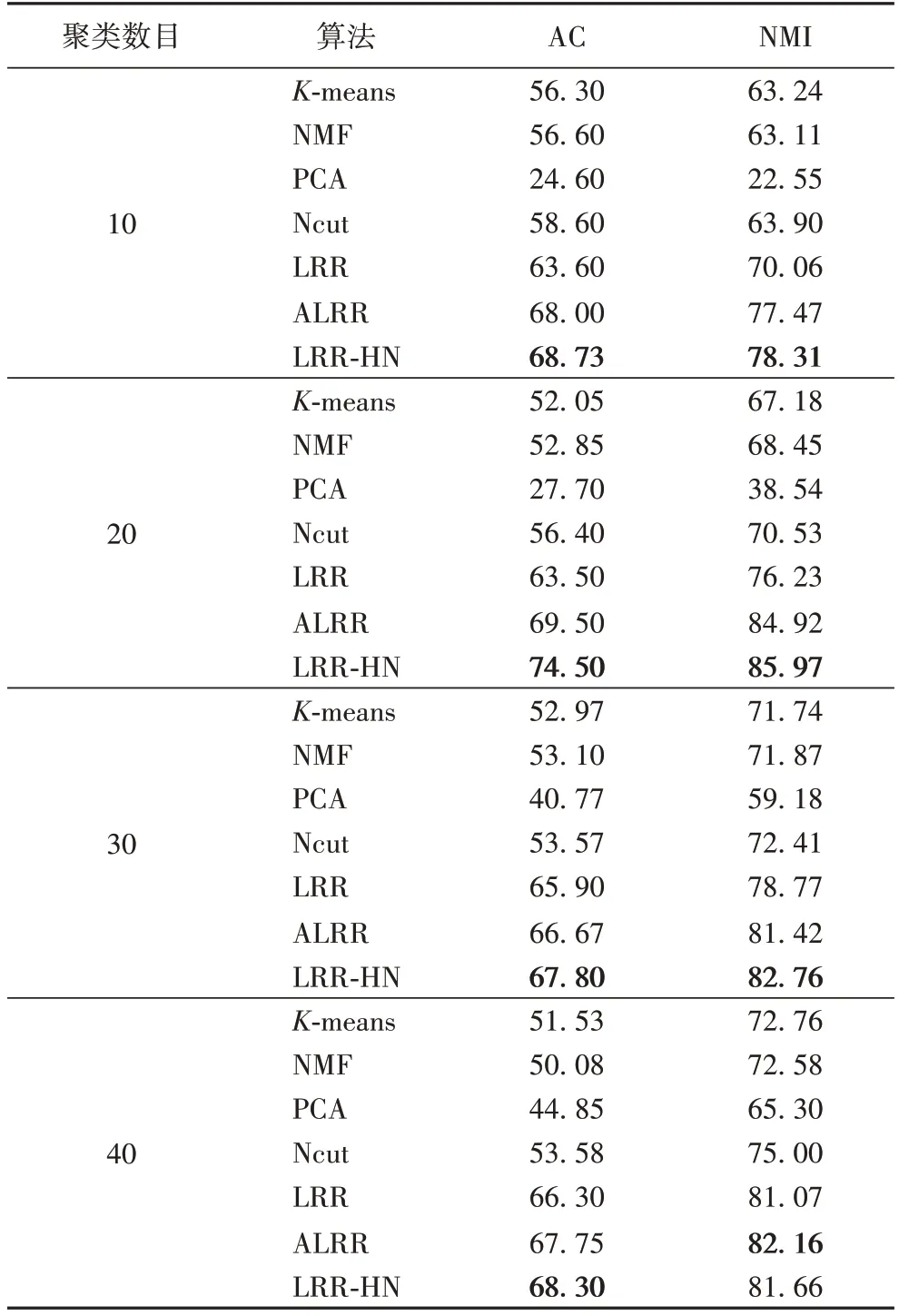
表2 不同算法在ORL数据集上的聚类结果 单位：%Tab.2 Clustering results of different algorithms on ORL dataset unit：%

表1、2中的每条数据都是重复进行20次实验取平均得到的。其中LRR和ALRR 算法的聚类结果是在源代码的基础上通过搜索选取最优参数获得的。由表1～2 中的数据可以看出，与经典的K-means、NMF、PCA、Ncut等算法相比，LRR 算法因低秩结构表现出了良好的聚类性能，AC和NMI的值远高于这些经典算法。ALRR 算法在低秩表示基础上增加了自适应性，实验结果表明，ALRR 算法的聚类结果在ORL 数据集上优于LRR 算法，在Yale 数据集上与LRR 算法不相上下。而本文提出的LRR-HN，在AC 和NMI 上均高于LRR 算法，且在大多数情况下优于ALRR 算法。这表明Hessian 正则项的引入和系数矩阵的非负约束能够更好地保持数据的局部拓扑结构，更能体现数据间的关联，从而提高算法的聚类效果。

3.3 不同参数对本文算法的影响

在本文算法中，平衡参数λ1、λ2和λ3的取值对聚类结果的影响较大。为讨论3 个参数对本文算法的影响，在本次实验中，采用固定其中两个参数，然后对另一个参数取不同的值来观察AC 和NMI 的变化。

在Yale 数据集上，设置聚类数目为15，λ1=1，λ2=1.5，λ3=0.4。固定其余两位参数的值，分别对λ1、λ2、λ3的不同取值进行实验，AC 和NMI 的变化曲线如图3～5 所示。从图3～5中可以看到，AC 在λ1取值为｛10-3，10-2，10-1，100｝，λ2取值为｛1.5，2，2.5，3｝，λ3取值为｛0.005，0.01，0.05，0.1，0.5｝时，AC 的变化相对较小。而NMI 在λ1和λ2的取值区间中起伏较大，但最优性能显著，在λ3的取值区间中变化基本平稳。

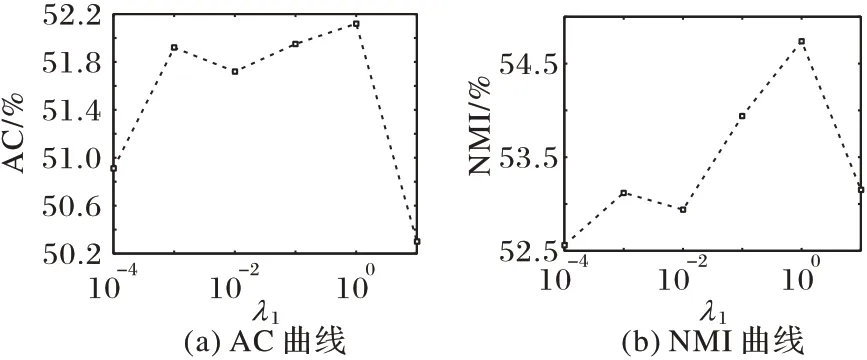
图3 Yale数据集上不同λ1时的AC和NMI变化曲线Fig.3 Change curves of AC and NMI with different λ1 on Yale dataset

在ORL 数据集上，设置聚类数目为40，λ1=10-3，λ2=1.9，λ3=1.1。固定其余两位参数的值，分别对λ1、λ2、λ3的不同取值进行实验，AC 和NMI 的变化曲线如图6～8 所示。从图6～8中可以看到，AC 和NMI 在λ1取值为｛10-6，10-5，10-4，10-3｝，λ2取值为｛0.5，1，1.5，2，2.5，3｝时，变化基本平稳，在λ3取值为｛10-3，10-2，10-1，100，101｝时，AC 和NMI 略有起伏，但变化不大。

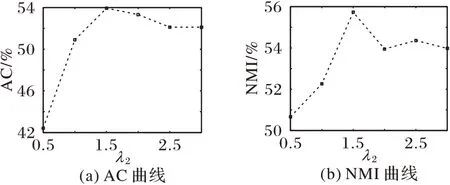
图4 Yale数据集上不同λ2时的AC和NMI变化曲线Fig.4 Change curves of AC and NMI with different λ2 on Yale dataset

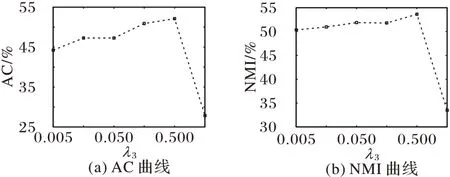
图5 Yale数据集上不同λ3时的AC和NMI变化曲线Fig.5 Change curves of AC and NMI with different λ3 on Yale dataset

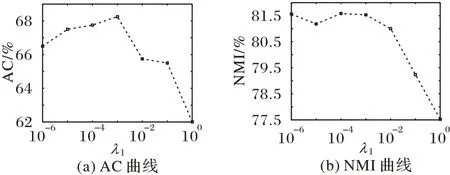
图6 ORL数据集上不同λ1时的AC和NMI变化曲线Fig.6 Change curves of AC and NMI with different λ1 on ORL dataset

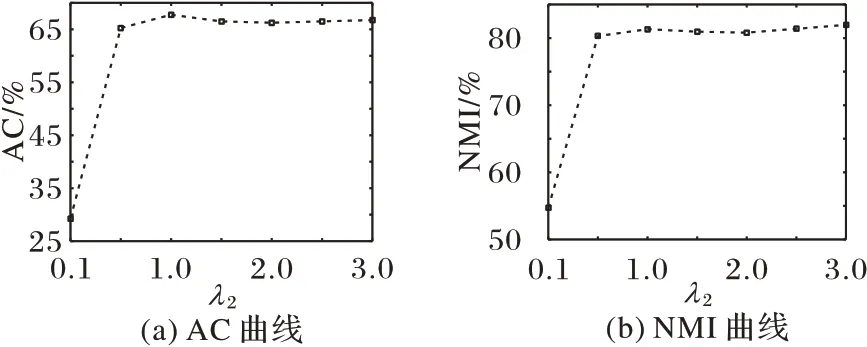
图7 ORL数据集上不同λ2时的AC和NMI变化曲线Fig.7 Change curves of AC and NMI with different λ2 on ORL dataset

从图3～8 可知，由于不同的数据集受噪声影响程度不同，平衡参数的最优值也不相同；但在合适的参数区间上，本文提出的LRR-HN表现出了较好的稳定性。

图8 ORL数据集上不同λ3时的AC和NMI变化曲线Fig.8 Change curves of AC and NMI with different λ3 on ORL dataset

4 结语

受流形学习思想的启发，本文提出了一种基于Hessian正则化和非负约束的低秩表示子空间聚类算法。首先，该算法利用核范数来探索数据的全局结构，使得来自同一子空间的高相关数据划分为同一类别。其次，引入了Hessian 正则项，采用近邻样本对数据线性表示，来加强数据间的局部相关性。为了更好地表征数据的局部结构，本文利用非负约束来保证解的有效性。最后，采用自适应惩罚的线性交替方向法求解，并在两个标准数据集上进行实验对比，表明了所提算法的可行性。