曲率半径对弯桥受力及变形的影响规律研究

林四新

(中交三航(厦门)工程有限公司 福建厦门 361003)

0 引言

近年来，国内外许多城市为减缓城市化建设而带来的汽车尾气及噪声污染、交通拥挤等一系列问题[1]，已逐渐开始建设享有独立行驶路权的自行车道[2-3]，以推进实现“绿色交通”[4]。在路线线形或城市立交互通的需求下，自行车桥由较多直线型与曲线型桥跨组合成联，弯扭耦合效应明显。由于自行车桥位于城市繁华地带，周边环境复杂，人流量大，在施工或运营过程中，一旦出现诸如梁体滑移、翻转，梁内支座托空等问题，后果将不堪设想。因此，为了确保桥梁的安全和质量控制，亟需针对不同曲率半径下自行车曲线桥受力情况及变形规律展开研究。

目前国内已有很多学者对常规曲线桥梁受曲率半径变化的影响进行相关探索，如牛俊武等(2011)[5]利用大型有限元通用程序ANSYS，采用时程分析方法，计算不同曲率半径下高墩大跨径连续刚构桥的动力响应，分别沿顺桥向和横桥向输入地震波进行分析，得出主要响应值峰值随曲率半径变化的规律；宋国华等(2011,2015)[6-7]以桥长和圆心角为参数，建立36个二等跨连续弯箱梁桥模型，采用非线性函数拟合法进行数据处理，拟合出极限状态下的截面配筋内力、单位位移及支承反力与圆心角和桥长的显式函数关系，得到各种结构反应受圆心角及桥长影响的变化趋势及程度大小，并以曲率半径为参数建立了4个两跨曲线箱梁桥模型，分析其模态特性及各振型方向因子随曲率半径的变化规律；孙珂等(2016)[8]在拟静力状态下测得弯梁桥竖向位移影响线(DIL)，通过二次差分获得影响线的曲率，结合缺口平滑技术构造损伤指标，实现对该类结构的损伤识别，以某三跨小半径弯梁桥为研究对象，建立相关数值模型来验证该方法的正确性及特点，对低速加载、支座预偏心及抗扭支座布置等对识别结果的影响进行分析；陈淮等(2013)[9]以某高墩大跨径预应力混凝土曲线连续刚构桥为研究对象，采用Midas/Civil有限元软件，建立直线刚构桥和不同曲率半径的曲线刚构桥有限元计算模型，分别对该桥梁施工阶段最大悬臂状态和成桥阶段进行静力力学性能分析，研究桥梁施工阶段最大悬臂状态、成桥阶段的曲率半径对连续刚构桥内力和变形的影响；王艳等(2014)[10]以某跨径组成为(95+170+95)m的高墩大跨曲线预应力混凝土刚构桥为背景，采用有限元程序Midas/Civil建立2组不同曲率半径和墩高的桥梁有限元计算模型，对其进行自振特性和地震反应谱响应分析；吴婷等(2011)[11]采用结构有限元计算方法，以世业洲互通D匝道桥工程为依托，基于曲线梁桥的受力特点，利用大型有限元分析软件ANSYS建立模型，计算不同曲率半径结构的变形情况；李杰等(2015)[12]以某双薄壁高墩曲线五跨连续刚构桥为实例，应用ANSYS有限元软件中的Solid 65实体单元和Beam 188梁单元建立该桥空间有限元计算模型，同时利用Midas/Civil建立大桥空间梁单元有限元模型，探讨不同软件、不同单元类型以及预应力张拉对双薄壁高墩曲线多跨连续刚构桥自振频率的影响，分析曲线桥梁结构的平曲线半径对双薄壁高墩曲线连续刚构桥的自振特性的影响，最后按照桥墩等线刚度的原则分析墩高对双薄壁高墩曲线连续刚构桥的自振特性的影响。尽管关于曲率半径变化对曲线梁桥结构影响的研究成果较多，但未见涉及自行车桥的相关报道。与常规公路桥、人行桥相比，自行车高架桥刚度更低，桥跨类型复杂，且部分路段在弯桥位置处还有分叉的情况，受曲率半径变化的响应特征不同。

基于此，本文采用有限元软件SAP2000建立有限元模型，分别选取5000 m、4000 m、3000m、2000 m、1000 m、500 m和250 m等7种不同曲率半径的2 m×20 m连续梁进行对比分析，研究弯桥结构的响应规律。

1 工程概况

厦门市自行车高架桥位于岛东部云顶路段，沿线与6处BRT站点、2处轨道站点、4处主要商业和行政办公衔接，总长约7.5 km。全线包含分离曲线段、曲线分叉段和单幅曲线段等较多曲线型桥跨，效果图如图1所示。自行车桥为独墩连续梁体系，桥梁断面分整幅式和分幅式2种，其中分幅式断面如图2所示。

图1 云顶路与仙岳路交叉处自行车专用道效果图

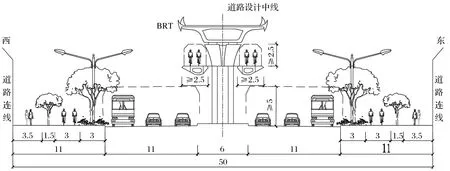
图2 自行车桥主线分幅式标准横断面图(单位：m)

2 数值模型设计

2.1 有限元模型

本次分析采用自行车桥分幅式钢箱梁，钢材材质为Q345，制造拆分图如图3所示。数值模型共划分13 041个单元，其中钢箱梁采用壳体单元模拟，每种曲率半径的双跨桥梁壳体单元数量为1863个，单元最大尺寸控制为1.2 m。网格划分如图4所示。模型按其实际尺寸确定计算参数：弹性模量E=2.06×108kN/m2、泊松比v=0.3、密度ρ=7.85×103kgm-3、重度γ=76.98 kNm-3、剪切模量G=7.69×107kPa、线膨胀系数α=1.17×10-51/℃。具体模型如图5所示，其中图5中从上至下模型的曲率半径分别为5000 m、4000 m、3000 m、2000 m、1000 m、500 m和250 m；两跨连续梁中间支座采取固定支座约束，两侧端部支座采取滑动支座，模型边界条件见图5(b)。

图3 分幅式钢箱梁制造拆分图

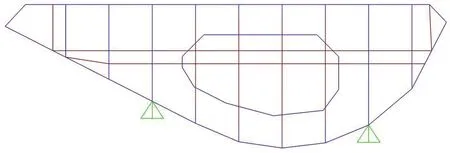
图4 自行车桥分幅式钢箱梁断面网格划分

(a)平面视图

2.2 计算工况

本次分析主要考察不同曲率半径模型在均布荷载作用下的应力和变形分布规律，其中均布荷载工况为桥梁的自身重量，共考虑28个计算工况，如表1所示。

表1 计算工况

3 计算结果分析

3.1 不同曲率半径下自行车弯桥挠度变化规律

桥面壳体单元的挠度沿跨度方向分布云图见图6，图中从上往下曲率半径分别为5000 m、4000 m、3000 m、2000 m、1000 m、500 m和250 m。

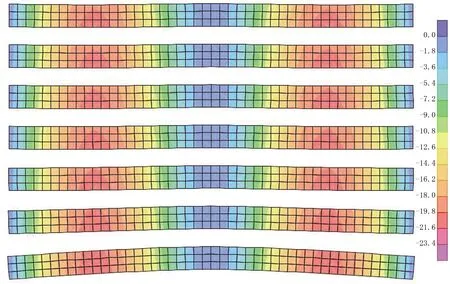
图6 不同曲率半径弯桥桥面挠度沿跨度方向分布云图(单位：mm)

从图6可以看出，总体上的挠度分布情况在不同的曲率半径下大致相同。但随着曲率半径的增加，跨中挠度略微有些增加。

3.1.1 跨中外侧挠度变化

均布竖向荷载作用下，跨中外侧挠度随弯桥曲率半径变化曲线如图7所示。

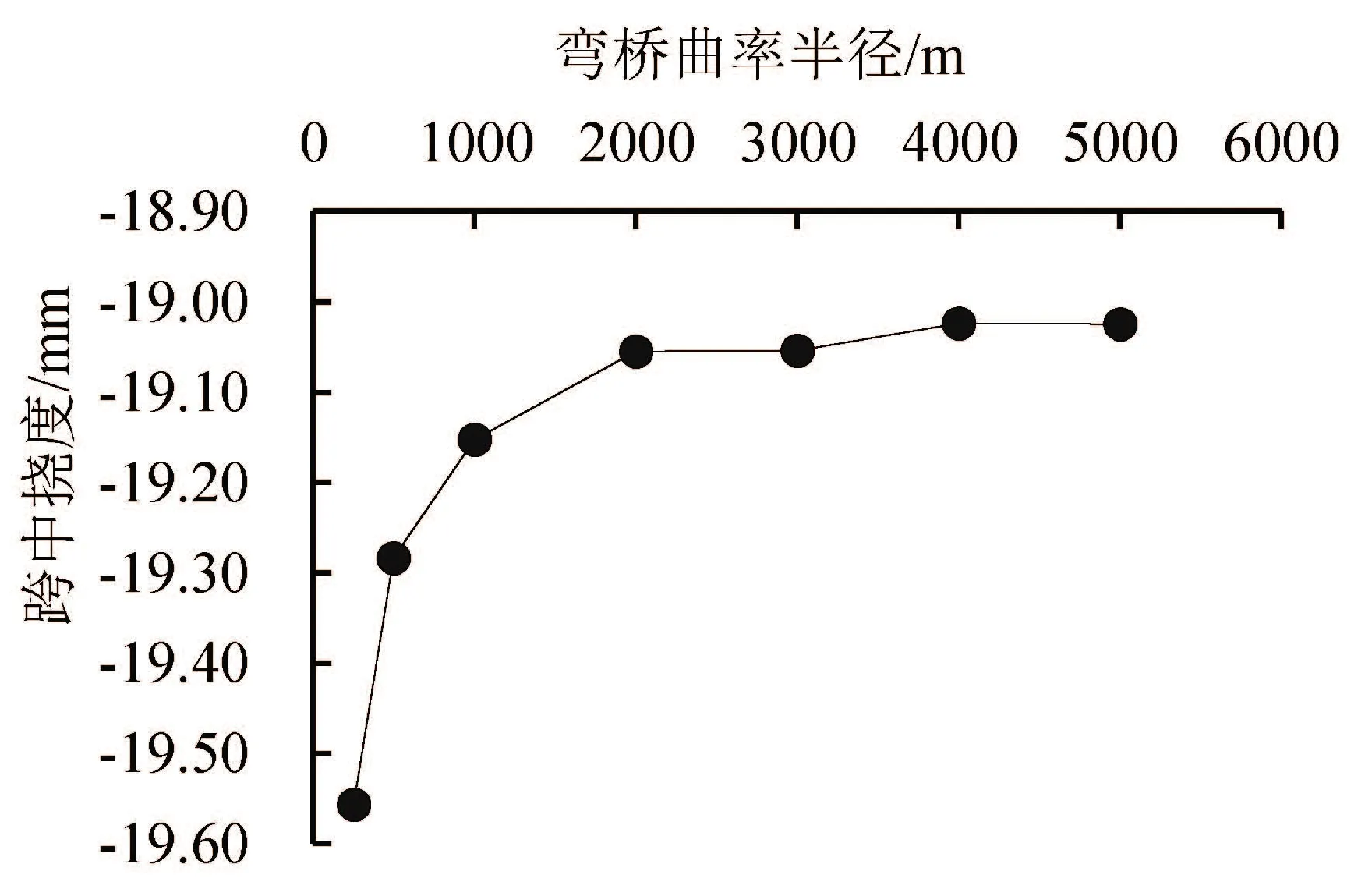
(a)左半幅

从图7(a)可以看出，左半幅跨中外侧挠度最大值发生在曲率半径为500 m的弯桥上，最大值为19.56 mm；最小值发生在曲率半径为5000 m的弯桥上，最小值为19 mm。曲率半径从500 m变化到5000 m时,弯桥跨中外侧挠度绝对值从19.56 mm单调减小到19 mm，由图7(b)可知，右半幅和左半幅挠度的数值和变化规律相近。

3.1.2 跨中内侧挠度变化规律

均布竖向荷载作用下，跨中内侧挠度随弯桥曲率半径变化曲线如图8所示。

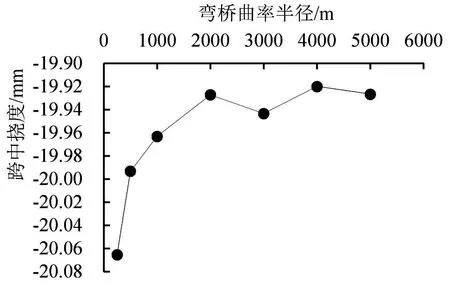
(a)左半幅

由图8可以看出，同桥面跨中外侧挠度变化曲线相似。当曲率半径为500 m时，弯桥的左半幅跨中内侧挠度出现最大值，为20.07 mm；当曲率半径为5000 m时，挠度最小，最小值为19.93 mm。曲率半径从500 m变化到5000 m时弯桥跨中内侧挠度绝对值从20.07 mm减小到19.92 mm，右半幅和左半幅挠度的数值和变化规律都相近，两者总体都呈上升趋势。

总体上，自行车桥跨中内侧挠度稍大于外侧挠度，无论是外侧还是内侧挠度，均随曲率半径的增大而减小，跨中挠度增大意味着抗弯刚度的减小。因此，根据上述数据可以推出，弯桥的抗弯刚度随着弯桥曲率半径的增大而增大。

3.1.3 扭转变形变化规律

在均布竖向荷载作用下，桥梁扭转变形主要体现在内侧和外侧的变形差上面。本次通过研究内侧和外侧的变形差，来定量分析桥梁扭转变形情况。跨中外侧挠度和内侧挠度差，随弯桥曲率半径变化曲线如图9所示。

从图9可看出，右半幅和左半幅两侧挠度差的数值和变化规律相似，随曲率半径的增加，挠度差绝对值也逐渐增大。曲率半径从500 m变化到5000 m时，弯桥跨中两侧挠度差绝对值从0.51 mm单调增加到0.9 mm。跨中内外侧挠度差体现了扭转变形的变化趋势，同时扭转变形增大意味着抗扭刚度的减小。由此可知，弯桥的抗扭刚度随弯桥曲率半径的增加而减小。

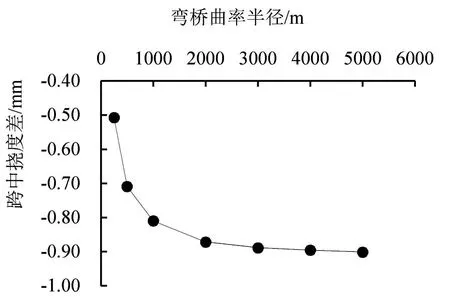
(a)左半幅

3.2 不同曲率半径下自行车弯桥支座反力变化规律

由上节分析结果可知，弯桥在竖向均布荷载作用下仍然会产生扭矩，而扭矩的产生将使得内外侧支座的受力不一致。本节主要研究不同曲率半径下支座内外侧的分布规律。图10为不同曲率半径弯桥在均布荷载作用下的支反力分布图。

3.2.1 外侧支座反力

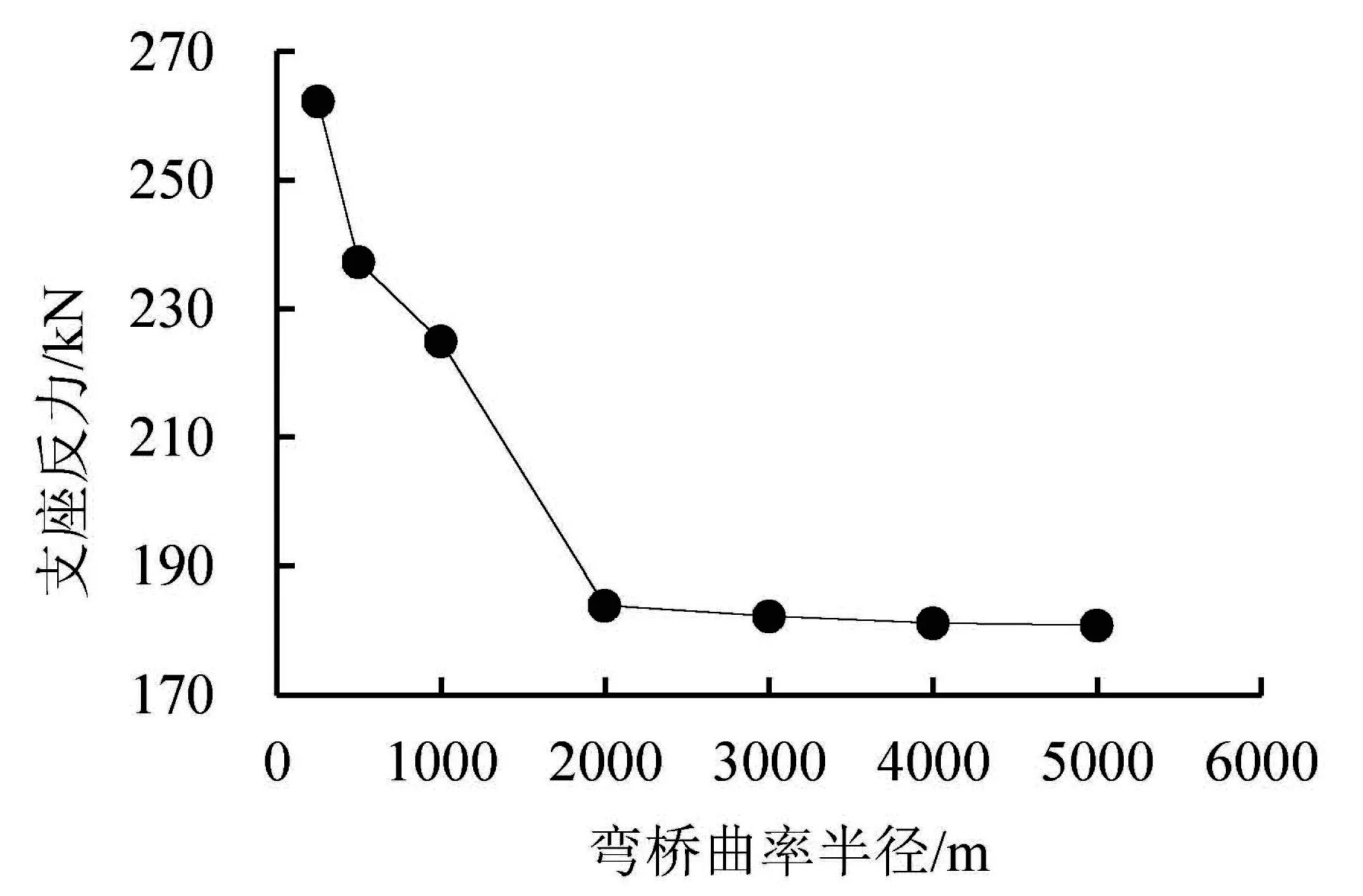
均布竖向荷载作用下，端部外侧支反力随弯桥曲率半径变化曲线如图11所示。

从图11可知，随着曲率半径的增大，右半幅和左半幅外侧支反力的变化曲线都呈现逐渐下降的趋势。左、右半幅端部外侧支反力的最大值均为262.2 kN，且都出现在曲率半径为250 m的弯桥上。最小值发生在曲率半径为5000 m时，最小值分别为180.8 kN和214.8 kN。

3.2.2 内侧支座反力

均布竖向荷载作用下，端部内侧支反力和两侧支反力差随弯桥曲率半径变化曲线分别如图12和图13所示。

由图12可以看出，内侧支反力随曲率半径变化曲线与图11外侧支反力随曲率半径变化曲线刚好相反。随着曲率半径的增大，右半幅和左半幅内侧支反力的变化曲线都呈现逐渐增大的趋势。左、右半幅的内侧支反力最大值分别为448.7 kN和414.7 kN，最小值均为370.7 kN。综合图13可知，外侧和内侧支反力差随着曲率半径的增加而增加。

(a)左半幅

(a)左半幅

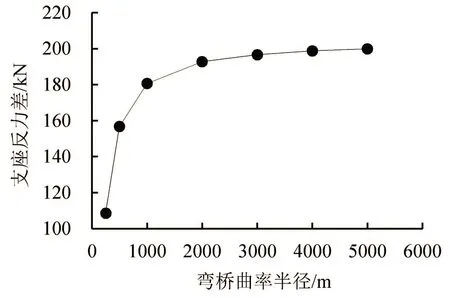
图13 外侧和内侧支反力差随曲率半径变化曲线

4 结论

通过本文研究可以得出以下结论：

(1)壳体有限元模型相对实体有限元模型而言，省去了大量实体同实体单元之间的连接，尤其是曲线段建模，实体模型很难有较好的适用性，采用壳体单元大大提高了建模效率。同时，由于实体单元仅存在平动自由度，没有扭转自由度，在上部结构与下部结构的变形协调方面，实体有限元模型也会带来额外的工作量，需要处理对应的连接处变形协调的问题。因此，在曲线钢箱梁高架桥受力分析时，采用壳体有限元模型，比实体有限元模型更有优势。

(2)自行车弯桥跨中内侧的挠度大于外侧挠度，跨中挠度随曲率半径的增大而减小，弯桥的抗弯刚度随着弯桥曲率半径的增加而增加；扭转变形随着曲率半径的增加而增加，自行车弯桥的抗扭刚度随着弯桥曲率半径的增加而减小。

(3)自行车弯桥同一支座位置处，外侧支反力随着曲率半径的增加而减小，内侧支座反力则随着曲率半径的增加而增加，内外侧支座反力随曲率半径的变化趋势正好相反；外侧和内侧支反力差随着曲率半径的增加而增加，同时不同的支座布置情况可能导致不同的影响。

(4)总体而言，影响弯桥的影响因子有很多，包括支座的几何布置情况、支座的限位措施导致的约束边界变化等，都会对弯桥的变形以及内力产生影响。此外，不同的受力工况得到的影响规律也将不同，限于篇幅，本文仅研究了两跨连续梁桥两端滑动的边界条件下，不同曲率半径桥梁在自重均布荷载作用下的规律，未综合考虑车道荷载、风荷载、汽车撞击等作用。因此，在后续分析中，有必要针对各种不利受力工况下曲率半径变化对薄壁弯箱梁桥的影响规律展开研究，从而为此类桥梁设计提供参考。