基于双层自适应遗传算法的机器人参数辨识

钟佩思， 刘金铭， 吕文浩， 张振宇， 宋庆军

(山东科技大学机电学院， 青岛 266590)

随着工业自动化的发展，要求机器人完成的任务越来越复杂，对机器人与环境交互能力的要求越来越高。要想提高机器人的控制精度，提高机器人与环境的交互能力，需要得到机器人准确的动力学模型，设计基于机器人动力学模型的控制系统[1]。参数辨识将理论建模和实验建模的优点结合起来，利用实验数据得到准确的机器人动力学参数，修正机器人的动力学模型[2-4]。

工业机器人动力学参数辨识流程包括动力学模型建立及其线性化、激励轨迹选取及其优化、辨识算法设计、参数采集与处理、实验验证[5-6]等。其中，激励轨迹的选取和优化是决定机器人动力学参数辨识是否精准的重要基础[7]。为了避免激发机器人的高频特性[8-9]，减少噪声干扰对参数辨识的影响，提高机器人动力学参数的辨识精度，需要选取合适的激励轨迹并对其进行优化。

常用的激励轨迹有三次、五次多项式、傅里叶级数及其改进等。刘磊等[10]引进S型函数优化收敛因子，提出了一种改进的基于S型函数的灰狼算法，扩大了算法的搜索范围，避免了算法的“早熟”。严浩等[11]采用基于排挤机制的小生境遗传算法对SCARA机器人前两关节的激励轨迹进行优化，没有考虑SCARA机器人其他关节的激励轨迹。张师源等[12]采用遗传算法优化了激励轨迹，没有考虑遗传算法易陷入局部最优解的缺点。Liu[13]等提出了一种基于改进的人工鱼群算法的辨识方法，证明了辨识方法的有效性。张铁等[14]使用lagrange法建立机器人的线性辨识模型，对六阶傅里叶级数进行优化，得到了六自由度机器人的激励轨迹，没有考虑优化算法。李家铮等[15]。通过递推最小二乘法获得辨识参数，提高了辨识的准确性。

针对上述问题，以SCARA机器人为研究对象，使用Newton-Euler迭代法建立机器人的动力学模型并进行线性化，以观测矩阵条件数最小作为优化目标，选择5阶傅里叶级数的作为激励轨迹，使用改进的双层自适应遗传算法进行优化，利用递推最小二乘法计算机器人的最小惯性参数集。

1 机器人动力学模型及其线性化

1.1 SCARA机器人动力学模型建立

SCARA机器人的空间定位精度由连杆1、连杆2和连杆3决定，将连杆4示为连杆3的负载，仅对前三个工作臂进行动力学建模。

利用Newton-Euler法求机器人动力学方程的具体过程分为两部分，第一部分从连杆0到连杆n向外迭代计算连杆的速度和加速度。第一部分根据关节类型又可分为两种递推方式。对于转动关节，外推公式为

(1)

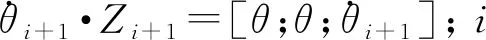
对于移动关节，外推公式为

(2)

第二部分从连杆n到连杆1向内计算连杆间的相互作用力和力矩以及关节驱动力矩，计算公式为

(3)

式(3)中：F表示驱动力；N表示驱动力矩；m表示连杆质量；I表示连杆坐标系的惯性张量矩阵。

根据Newton-Euler迭代法的计算步骤，利用MATLAB编写迭代计算程序，计算得到自由运动SCARA机器人各关节力矩[f1;n1][f2;n2][f3;n3]。

因为关节1、2为旋转关节，关节3为移动关节，且各关节的旋转轴均为Z轴，得到各关节的驱动力矩为

(4)

1.2 模型线性化

因为机器人的动力学模型是其惯性参数的线形函数，故可将机器人动方程线性化为关节驱动力矩与惯性参数的表达式，即

(5)

式(5)中：Y是大小为n×10的观测矩阵；n为连杆数量；P为待辨识惯性参数集，P={xx1xy1xz1yy1yz1zz1mx1my1mz1mi}。

由于SCARA机器人动力学模型较为简单，采用数学推导的方法，依次确定连杆3至连杆1的最小惯性参数和观测矩阵为

(6)

2 激励轨迹及其优化目标

机器人在激励轨迹中达到的位姿越多，测得的动力学参数信息就越全面，动力学参数的辨识精度就会越高；同时，为了减少噪声干扰对参数精度的影响，需要在进行激励轨迹优化之前需要选择合适的激励轨迹模型，避免激发机器人的高频特性。

2.1 改进的傅里叶级数

关节i角度的改进傅里叶级数公式为

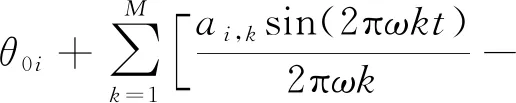
(7)

根据式(7)可得关节i角速度和角加速度表达式为

(8)

改进的傅里叶级数可以满足连续性、周期性和运行的平稳性，在轨迹起始和停止的位置，关节i的角速度和角加速度为零，满足上述要求的约束条件为

(9)

式(9)中：ts和tf分别为轨迹起始时刻和终止时刻，θs-f为起始和终止时刻关节角。

利用式(9)中的4个约束条件，可得改进傅里叶级数中五次多项式的系数为

(10)

2.2 轨迹优化目标

在进行动力学参数辨识的过程中，N阶动力学参数辨识方程τN=YNp由N组观测数据组成回归矩阵YN和关节驱动力矩矩阵τN组成。当YN和τN存在扰动δYN和δτN时，N阶动力学参数辨识方程为

(τN+δτN)=(YN+δYN)(p+δp)

(11)

联立式(5)，两式相减可得

δτN=YNδp+δYNδp+δYNp

(12)

由式(12)推导可得

(13)

对式(13)两边取范数可得

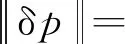
(14)

进一步化简可得

(15)

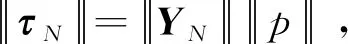
(16)

最终可得待辨识参数集p的相对误差为

(17)

根据定义可知，回归矩阵的条件数为

(18)

将式(18)代入式(17)可得

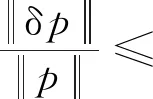
(19)

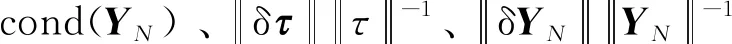
3 双层自适应遗传算法

在遗传算法中，直接影响算法的收敛性。传统的遗传算法，遵循选择、交叉和变异的顺寻，但在种群相对集中的情况下，交叉的意义不大，种群依然有可能陷入局部最优解[16-18]。因此，提出顺序自适应机制，通过判断种群的集散程度，确定交叉和变异的顺寻。当种群较为集中时，先进行变异操作，跳出局部最优；当种群较为发散时，则先执行交叉，再进行变异。

此外，交叉概率大，容易使优良基因被破坏；交叉概率小，旧的基因不容易被破坏，容易导致算法早熟。变异概率过小，不易形成新的个体，降低了全局搜索能力；变异概率过大，则增强了随机性，增大了全局搜索时间。并且引入概率自适应调整函数，使交叉概率和变异概率跟随个体适应度大小和群体的分散程度进行自动调整。如图1所示为改进的自适应遗传算法的流程。

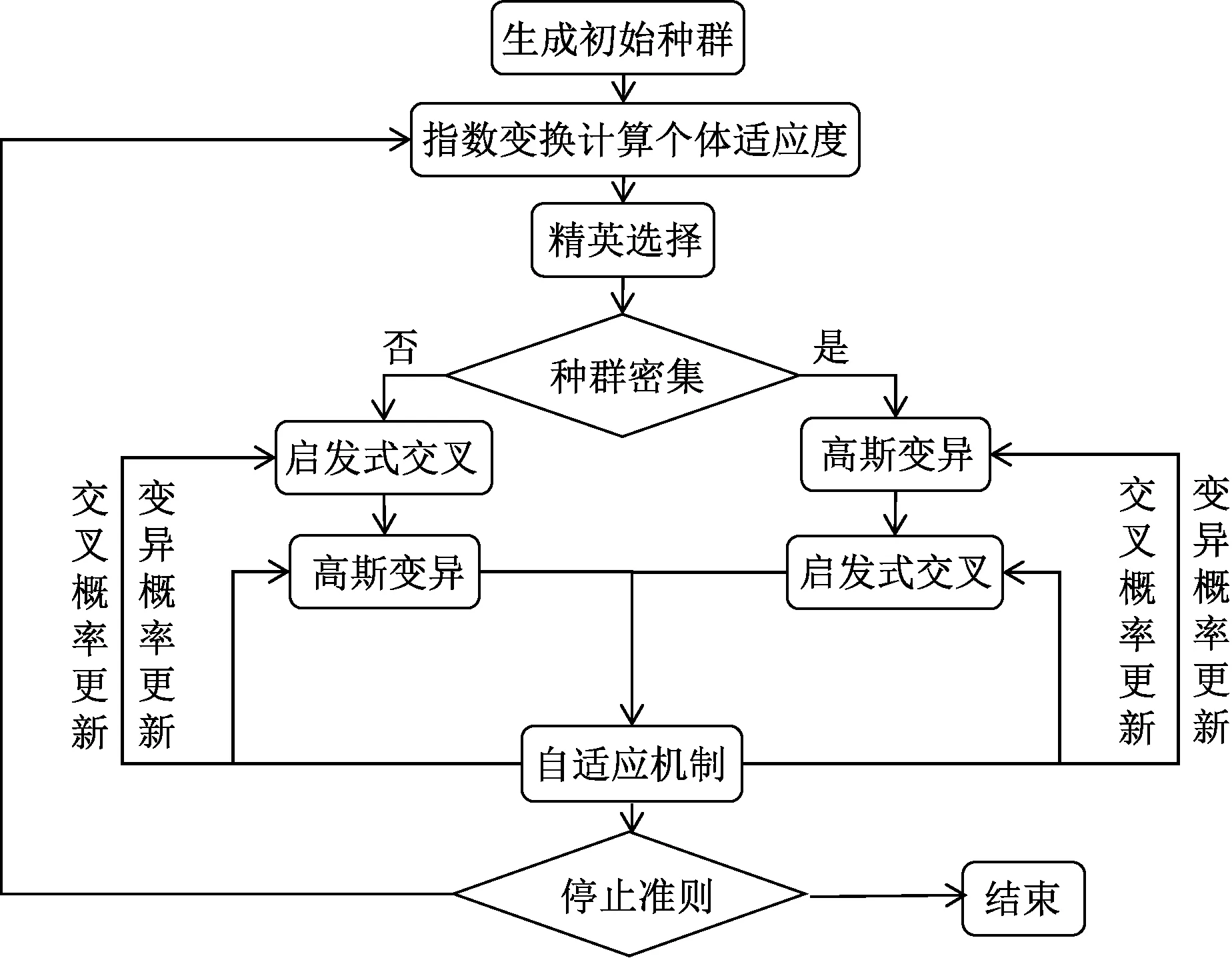
图1 改进自适应遗传算法流程

利用当代种群适应度的最大值和平均值作为评判标准，完成对群体集散度的判断和对交叉概率Pc和变异概率Pm的调整。概率自适应调整函数为

(20)

(21)

当个体最大适应度大于当代种群中的平均适应度时，认为个体性能较好，则降低交叉概率Pc和变异概率Pm以尽可能保存其优良特性；当个体最大适应度小于当代种群中的平均适应度时，认为个体性能不佳，则增大交叉概率Pc和变异概率Pm以加快个体更新速度。群体集散度判断函数为

(22)

式(22)中：fmax是当代种群中的最大适应度值；favg是当代种群中的平均适应度值。

如果群体适应度满足该公式，则先认为群体足够离散，执行交叉变异；否则，先执行变异再进行交叉。

4 激励轨迹优化与参数辨识实验

4.1 激励轨迹优化

经过上述分析，最终可以确定改进的傅里叶级数的轨迹优化目标为观测矩阵条件数，利用改进的自适应遗传算法获得全局最优化的系数ai,k、bi,k、b0，具体的约束条件为

(23)

式(23)中：SCARA机器人各关节角度、角速度、角加速度的限制范围如表1所示。

表1 关节运动限制范围

在简化后SCARA机器人中，连杆1、2的转动和连杆3的移动是解耦的。因此，分别求取前两关节和关节3的激励轨迹。

根据式(6)可知，前两关节和第三关节的观测矩阵为

(24)

选择改进的5阶傅里叶级数作为激励轨迹，分别以式(23)中①、②条件数的表达式cond(Yr)作为目标优化函数，共有30个待优化参数。设置基频ω=0.2π，迭代次数设置为400代，种群大小设置为60，交叉概率Pc设置为0.5，变异概率Pm设置为0.5。优化结果如表2所示，改进自适应遗传算法得到的前两关节和第三关节的观测矩阵条件数分别为1.041 4和1.000 0。

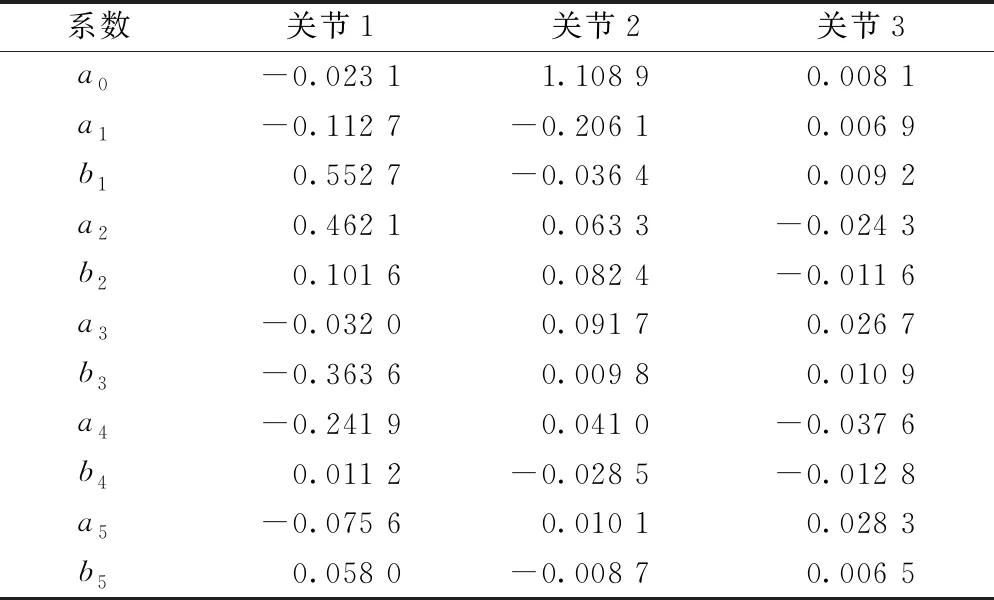
表2 最优化傅里叶级数系数

4.2 参数辨识实验

为了验证本文提出的激励轨迹优化算法的可行性与可靠性，利用MATLAB和ADAMS进行联合仿真。因为SCARA机器人第三关节与前两关节解耦，所以分别对前两关节和第三关节进行参数辨识仿真实验。

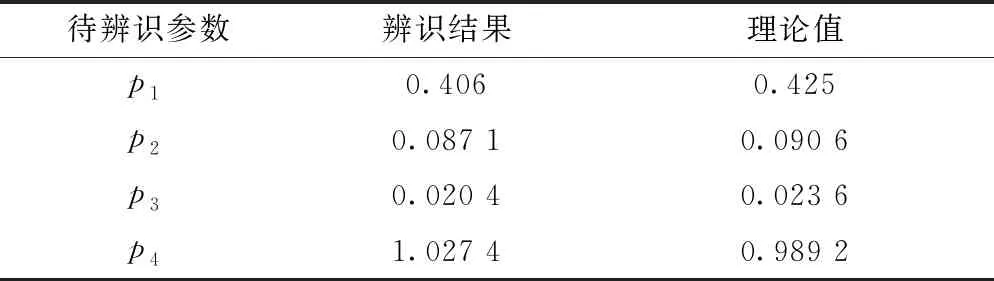
表3 参数辨识结果

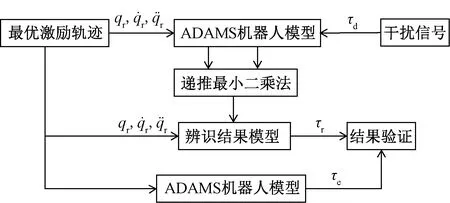
图2 动力学参数辨识仿真与验证流程图

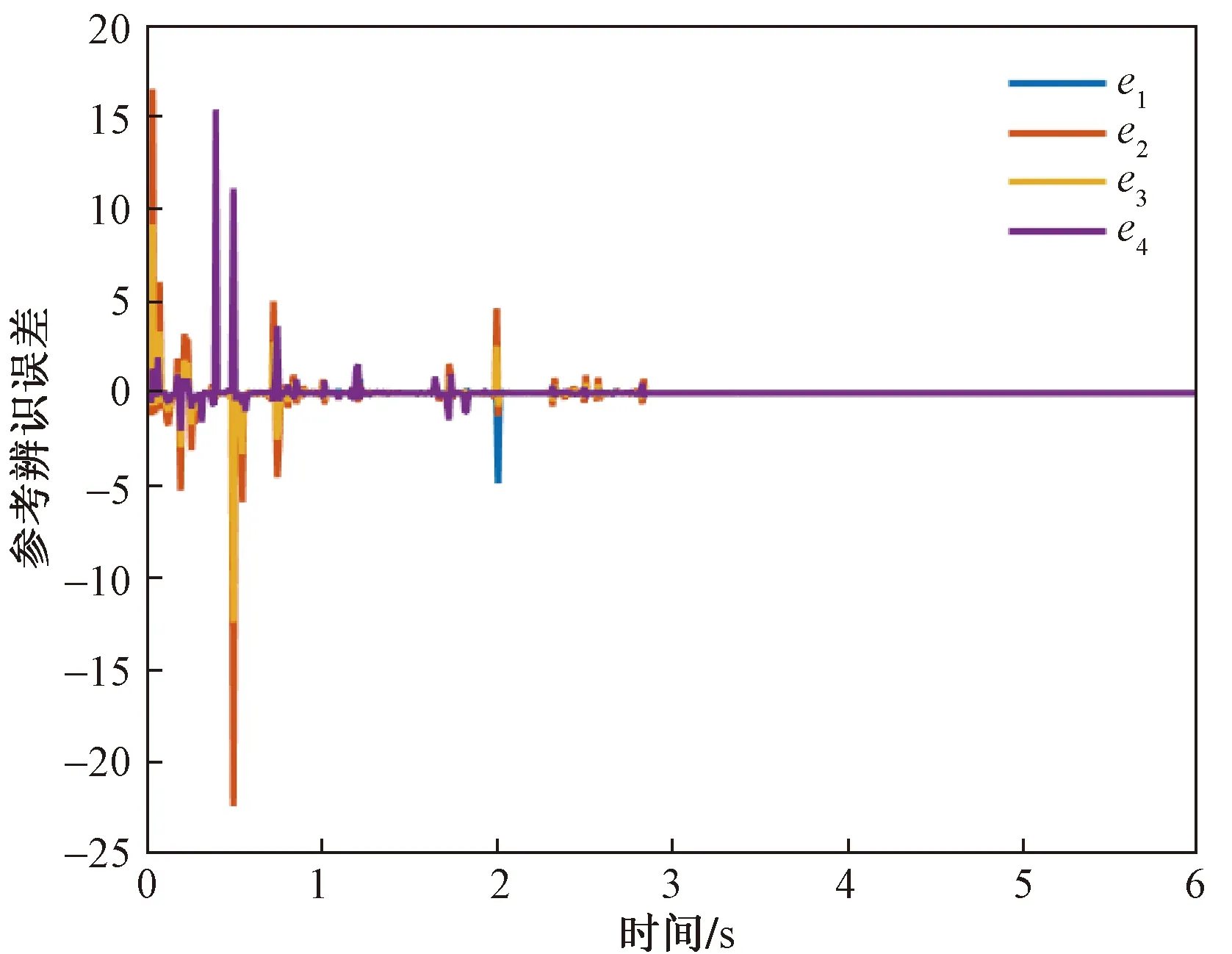
图3 待辨识参数误差收敛过程

将辨识结果代入机器人的动力学模型中，得到参数辨识模型。将轨迹作为输入，对比辨识模型和ADAMS物理模型输出的关节力矩。图4所示为各关节的辨识模型和ADAMS物理模型输出的力矩对比曲线。

根据图4所示的仿真结果可知，辨识模型与ADAMS物理模型得到的3个关节的力矩曲线整体趋势大致相同，数据也基本吻合。为了更好地表征理论计算值与实测值之间的偏离程度即误差，分别利用平均绝对误差和均方根误差来分别对其进行描述。平均绝对误差与均方根误差的表达式为

(25)

根据式(25)计算得到的各关节平均绝对误差与均方根误差如表4所示。

表4 各关节误差评价指标

根据图4中的信息可知，使用理论模型得到的理论力矩与使用辨识模型得到的辨识力矩在数值上和变化趋势上均大致相同。根据表4的数据可知，使用双层自适应遗传算法得到的激励轨迹，提升了机器人的动力学参数辨识精度[15]。

第一关节的均方根误差和平均绝对误差最大，这是由于第一关节的电机力矩最大。总的来说，实验结果较为理想，证明了辨识结果的准确性和改进遗传算法优化方案的可行性。

5 结论

(1)采用Newton-Euler法建立了SCARA机器人的动力学模型，并采用数学推导的方法对模型进行线性化和参数分离，得到了SCARA机器人前三关节的观测矩阵和最小待辨识参数集。

(2)选择改进的傅里叶级数作为激励轨迹，分析辨识参数辨识方程，确定了观测矩阵条件数最小的优化目标。对遗传算法进行改进，提出了双层自适应机制，确定了基于双层自适应机制的激励轨迹优化方案。

(3)使用MATLAB和ADAMS进行联合仿真实验，基于递推最小二乘法得到了机器人的最小惯性参数集。实验结果表明，使用双层自适应遗传算法得到的激励轨迹可以保证机器人动力学参数辨识的精度。