基于强化学习的应急物资动态模型配送算法优化

李攀， 周兆军， 孙晓叶， 陈福明

(1.防灾科技学院信息工程学院, 三河 065201; 2.河北省地震灾害防御与风险评价重点实验室, 三河 065201; 3.防灾科技学院继续教育学院, 三河 065201)

中国为地震多发国家,为挽救更多人的生命,减小人们的财产损失,国家非常重视灾害应急救援工作。在2008年后,更加重视应急物流管理制度的健全工作,完善了应急物流预案,并提前储备了对应的帐篷、衣被、净水设备和药品等；定期开展了应急物流的宣传和演习工作；在城市中分散建立了应急物资库；规划了海陆空的运输替代路线等措施[1]。周愉峰等[2]提出一种整数编码的混合遗传算法,通过三角模糊数的期望值公式将模糊需求去模糊化,考虑设施中断情景后,物流配送的情况,建立适用于震后救援初期的应急设施选址-分配模型。Kaveh等[3]将应急管理问题,规划为四大方面,应急反应规划、大规模疏散、庇护所选址和设施选址,并归纳了不同技术路线上,启发式优化算法的模型及应用。Zhao等[4]基于泊松混合模型,提出一种新的地震伤亡早期预测模型,同时模拟三种主要伤亡类型,有助于政府及时制定全面的救援方案。模型中引入了两个新的协变量:“距离”和“余震”,这可以显著改善模型预估成果。Yao等[5]基于新浪微博,提出了一种从微博文本中提取烈度信息的方法,包括摇晃、应急反应、情绪和可见损伤等社会感知,为地震烈度的快速评估提供支持。还提出了一个基于网格的校正方法,它综合了热强矩阵和基于地震衰减的模型,显著降低了错误识别率。

地震发生后,如何对受灾民众进行最快的救护,如何快速进行救灾物资配送,是应急救援的首要任务。相关的学者们,针对以上问题,进行很多研究,构建不同模型。李珍萍等[6]以家电企业配送与安装物流作业问题为场景,采用遗传算法,优化目配送与安装两种工作的车辆行驶路径问题,以总成本最小为目标,考虑配送车辆的软时间窗约束与安装车辆的服务水平约束,但车辆只能从同一地点出发,返回同一地点,极大约束了车辆流动范围。牟向伟等[7]使用量子进化算法,针对末端配送任务分配问题建立了一种考虑配送成本、资源利用率以及工作量配比差异的配送任务分配模型,但是配送能力在救援过程中不会发生变化,模型无法动态更新。现设计动态变化的道路模型,及不同种类的车辆数据,载重和运力都不相同,目的就是解决实际面对的真实场景,发生的多维度问题。康斌等[8]提出优先邻点交叉算子来改进基于非支配解排序的遗传算法,提高了局部搜索能力和收敛速度。采用了需求未满足率来保证配送公平性,但是救援物资仅考虑一般生活物资,未能考虑应急救援初期,是医疗物资和生活物资都急需,而且更重视医疗物资,需要合理分配任务的问题。崔洪军等[9]建立以最小化道路权值为目标,同时考虑车辆自身对道路条件约束的路径规划模型,对道路综合权值的设计方案,为本文的网格化道路模型,提供了启发,本文在其基础上综合考虑路段长度、道路等级、拥堵情况、路面状况和路段坡度五个因素对路段综合权值的影响。对道路及周边建筑进行了网格化管理及赋值,可以实时动态反应道路的通行状况,安全系数,及对未来通行能力进行预测,提前规避可能发生危险和拥堵的道路,使得模型动态的计算最优解。

在面对重大自然灾害,应急物资配送大多数采取道路可靠多目标优化方法[10],但是没对物资的占用体积,重量,结合车辆的承载力进行考虑,同时没考虑到灾情是随时间变化的,每个受灾点需要的物资也是不同的,物资需求未能考虑,物资配比问题未加入考虑；道路路况是变化的,未加入考虑；针对车辆分配公平性和配送时间长短,构建多目标优化配送方法[11],但是考虑的要素是配送中心车辆充足,且车型相同,每辆车只执行1次配送任务,车辆的行驶速度不变,这种理想状态,在现实的灾区很难实现,救灾初期,面临的最大可能就是救援力量的缺乏,所以才需要合理安排时间和规划路径,实现最优解决方案；针对受灾人数不确定、信息不畅通、基础设施受损对后续灾害的造成影响等因素提出应急配送方法[12]；还有学者[13]应用改进的蚁群算法和遗传算法,提出应急物资配送不同的思路和解决方案,但是从成本和客户满意度出发,基于遗传蚁群算法规划了冷链配送路径,但是只考虑了一个配送中心,和应急救灾的逻辑有出入。配送的核心出发点,时间,成本于大部分同类算法一致,增加了空置率的控制条件,可以相应调节运输的效率,而蚁群算法的引入,也为最优路径搜索,提供了技术支撑。综上所述,目前应急物资配送领域的研究,主要基于配送时间最短、物资配送数量最大、配送成本考虑,对于道路的实时畅通拥堵情况和多因素综合实时影响方面考虑较少。因此,针对中大型地震灾害发生时,进行救援规划,提升救援组织能力,提出一种事先训练好的强化学习算法优化模型,以挽救更多的受伤民众为核心目标,可以提前演练可能出现的种种救援临时状况,让算法系统学会不同情况的应对,在实时计算时,只需导入相关数据,即可快速求解出最优配送路径。不仅考虑灾情紧急时刻的物资短缺,车辆短缺情况,还引入动态数据,实时更新道路,交通,危险建筑对配送路径的阻碍关联,更新需求物资的变动,从医疗物资到生活物资；并引入独特的紧急因子,用于判断运输的不同相应模式,以适应从前期紧张到后期缓和的配送方式。并根据中国国情,在后期高速公路入库引入新建的物资集散地概念,会导致物资从城外运输的路径获得更多解,从而大大优化物资配送效率,提供运力,单位时间内满足更多救灾物资需求,拯救更多民众的生命。

1 问题分析

假设城市对外交通运输能力(机场、铁路和高速公路其中之一)没有完全断绝,可以满足物资持续不断运输进入城市,同时城市本身的固定安置点和应急安置点已被相关社区人员妥善管理,城市通讯在中断后已基本恢复正常,可以更新应急物资的需求,及时安排运输车辆和储备仓库的物资调运。城市内部道路会受到余震、电力、热力、燃气、给排水或建筑倒塌造成损坏。因此,不同类型的道路会出现通行或拥堵等风险情况。根据城市中每条道路的损坏程度,可对每辆运输车、每种物资和每条线路进行设计,在规避风险道路同时,实现运送应急物资车辆的最大化运力。地震发生后初期,所运送的物资中,医疗物资是最重要的,随着救援的时间的延长,受灾人员的食品、衣服和临时居住场所等需求量,将逐步超过医疗物资,成为主要的输送物资。因此,本文中将应急物资配送的过程分为3个主要阶段。

(1)救援初始阶段：应急物资来源主要是城市本身的物资储备仓库,配送模型的模式是运输车辆在城市内部循环,运输车的数量,单位时间运力最大程度,不能超出车辆数量、载重量和载重体积的限制；而且随着时间进展,物资储备仓库的物资消耗速度是不同的,物资量根据实际不同物资的性质,不同需求量,实时进行变化。

(2)救援中间阶段：随着对外连接道路的打通,在城市外接高速路口,机场或火车站的集散仓库,会建立临时物资集散地,物资的流向是外围充足,内部匮乏的阶段,类似于一个盆地地形的水流流向的走势,由外向内的漩涡形态。

(3)救援最终阶段：由于前期重伤员及时得到救治或转移,城市内只存在轻伤员和普通群众的阶段,这时外援力量已经足够大,运输物资的压力逐渐减轻,需要合理的安排运输车辆的数量、频次和路线,为其他救援单位(如建筑、工程、水力和电力等)的往来减轻交通压力。

根据以上分析,该算法模型需要使用的数据为：城市基础静态数据,包括医疗机构和危险建筑或设施的信息；物资静态数据,包括储备仓库,主要分为医疗物资和生活物资等；高速路口、机场和火车站静态数据,用于建立临时物资集散地,震后根据高速公路路网、火车站、城市机场周边位置,可在第一时间兴建外援物资集散地,可以实时输送各种应急物资,默认外援物资集散地设置在高速公路与城市主干道连接处,火车站和机场周边；灾民安置点静态数据,安置点主要提供需要生活物资和少量医疗物资；物资运输车辆静态数据,包括车辆的类型、车辆的体积和重量等信息,还有道路静态数据包括道路的等级和路况等信息。

2 模型构建

2.1 物资配比模型

为了使车辆装配运输物资效率最大化,需要考虑车辆装载物资类型、数量和大小进行优先级设置。地震发生时,抢救人民群众的生命是最重要的,因此医疗物资是优先级别最高,其次是生活所需的各种物资,同时汇总物资仓库信息,运送范围的受灾人员安置点信息和最新物资数量等信息,具体处理步骤如下。

(1)设定λ为救援优先级因子,取值范围为0和1之间,当λ=1时,表示地震初期,受伤民众较多,主要物资配送集中在医疗物资方面,当前各项物资消耗快,剩余紧张,灾民增加过快,运力严重不足,因此此情况下需要全力满足医疗物资的运输。当有空闲运力时,才能安排生活物资运输,而且以饮用水优先,非常紧急时可以完全不配送食物；当λ=0时,表示当前物资消耗速度不快,灾民增加速度慢,可以降低运输效率,所以配送物资的数量存在上调可能,即发出的物资甚至会大于需求数量。根据应急救援的人为经验,规定当λ>0.7时,为运输紧急状态；当0.3<λ<0.7时,为中等运输状态；当λ<0.3时,为缓和运输状态。

(2)设置物资权重系数Whi和Wli,分别为医疗物资权重和其他生活物资权重。

总物资权重为W={W1,W2,…,Wn},其中Wi为

Wi=Whi+Wli,i=1,2,…,n

(1)

根据震后现场受伤人员数量,应急物资储备数量及地震的破坏程度等综合因素分析,物资权重的具体取值如下。

当λ>0.7时,Whi的取值范围为0.8～1.0,Wli的取值范围为0～0.2。

当0.3<λ<0.7时,Whi的取值范围为0.5～0.8,Wli的取值范围为0.2～0.5。

当λ<0.3时,Whi的取值范围为0.3～0.5,Wli的取值范围为0.5～0.7。

(3)设置通用物资包集合为:M={M1,M2,…,Mn},单个物资包为Mi,表达式为

Mi=Su1n1+Su2n2+…+Suini,i=1,2,…,n

(2)

式(2)中：Sui为第i个储备物资包的体积和重量集合;n为根据需求进行分配物资的数量。

假设总物资需求数为Ni,每辆车上装配物资为

Tall=MiWhi+MiWli,i=1,2,…,n

(3)

根据各个物资点的需求,计算对应的车型,所能规划的物资包设计,以最优化方法为目的,尽可能先运输优先级靠前的物资,这里采用优先级因子λ参与,将需要的物资包种类先规划出来,然后规划车辆,根据装卸先进后出的特点,先配送物资后装车,并且在车子到达前,就需要发给仓库打包,然后车辆到达就直接装箱,并按照装卸顺序进行排列安装。

2.2 道路状况模型

本文中建立道路状况模型,通过路况来进行路径计算,由于震后交通形势复杂,道路中存在断路、道路不通或者严重拥堵问题,不能直接使用曼哈顿距离。本文中添加道路运载情况和危险建筑等动态数据,在模型中考虑这些因素的影响。首先对城市基础数据进行网格化划分,每个网格的属性点数据由运行通畅能力和安全系数等因素所决定,将这些参数进行叠加就可以得到道路的运行情况,然后车辆的最终运输路径,采用迭代法进行处理,预测结果不唯一。已知类曼哈顿距离方程D[14-15]为

D=|xi-xj|+|yi-yj|,i=1,2,…,n;

j=1,2,…,n

(4)

式(4)中：(xi,yi)为相邻每个网格化点的坐标。在此模型中引入路况因子β,该因子大小决定道路是否畅通,每条道路通畅与否由多个网格属性合集决定：βall={β1,β2,…,βi}(i=1,2,…,n),其中,每项的计算公式为

(5)

式(5)中：w为道路的宽度；l为道路的等级；ɑ为实时道路拥堵状况因子；γ为道路的危险性。

设置本路线通畅度C为

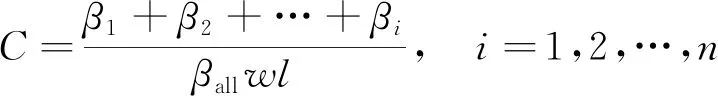
(6)

该算法可将附近所有可能产生的路径,都遍历迭代处理,计算每两个位置的多种运输路线。路线计算受网格状态影响,不能通行的地方,不参与计算,不会产生规划路径。

3 算法设计与优化

3.1 车辆运行路径模型优化

运输车辆要将各种物资配送到各个目的地,因此本文主要研究图层为医疗单位(H)图层、物资仓库(S)图层、受灾人员安置点(G)图层、危险建筑(B)图层和临时物资集散地(D)图层共计4个图层。在受灾初期,外来救援力量还没有及时赶到受灾地进行救援时,可将本地仓库集合S进行三角剖分,计算得出Voronoi图,确定每个物资出发后所到达空间范围,如图1所示。

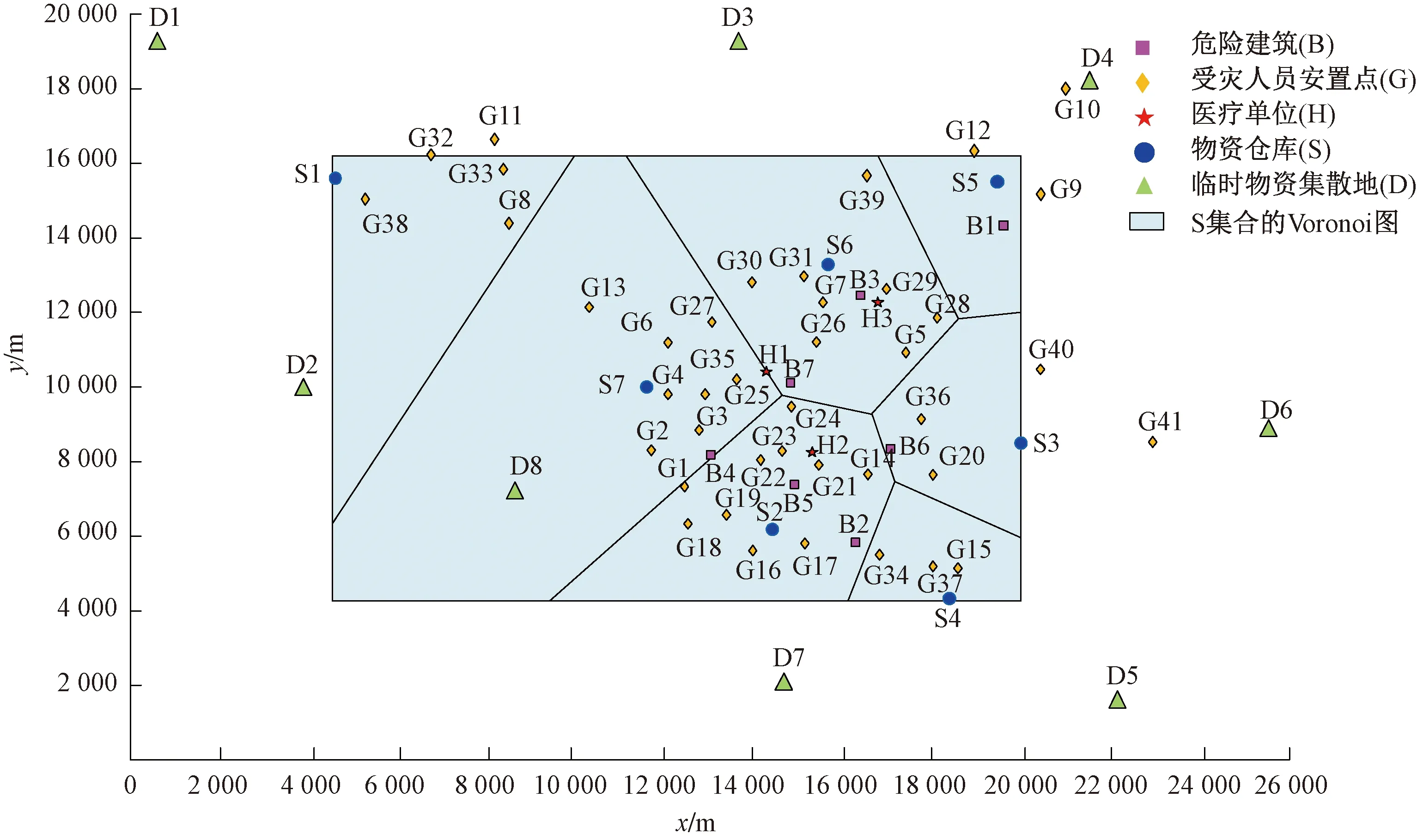
图1 S集合的三角剖分Voronoi图

随着救援时间的推移,外来救援队已到达城市高速路口、机场或者火车站等地,并建立临时物资集散地,这时将物资数据集合S和临时物资集散地集合D合并考虑,进行三角剖分,所得到Voronoi图如图2所示,得到每个物资出发到达的新范围。

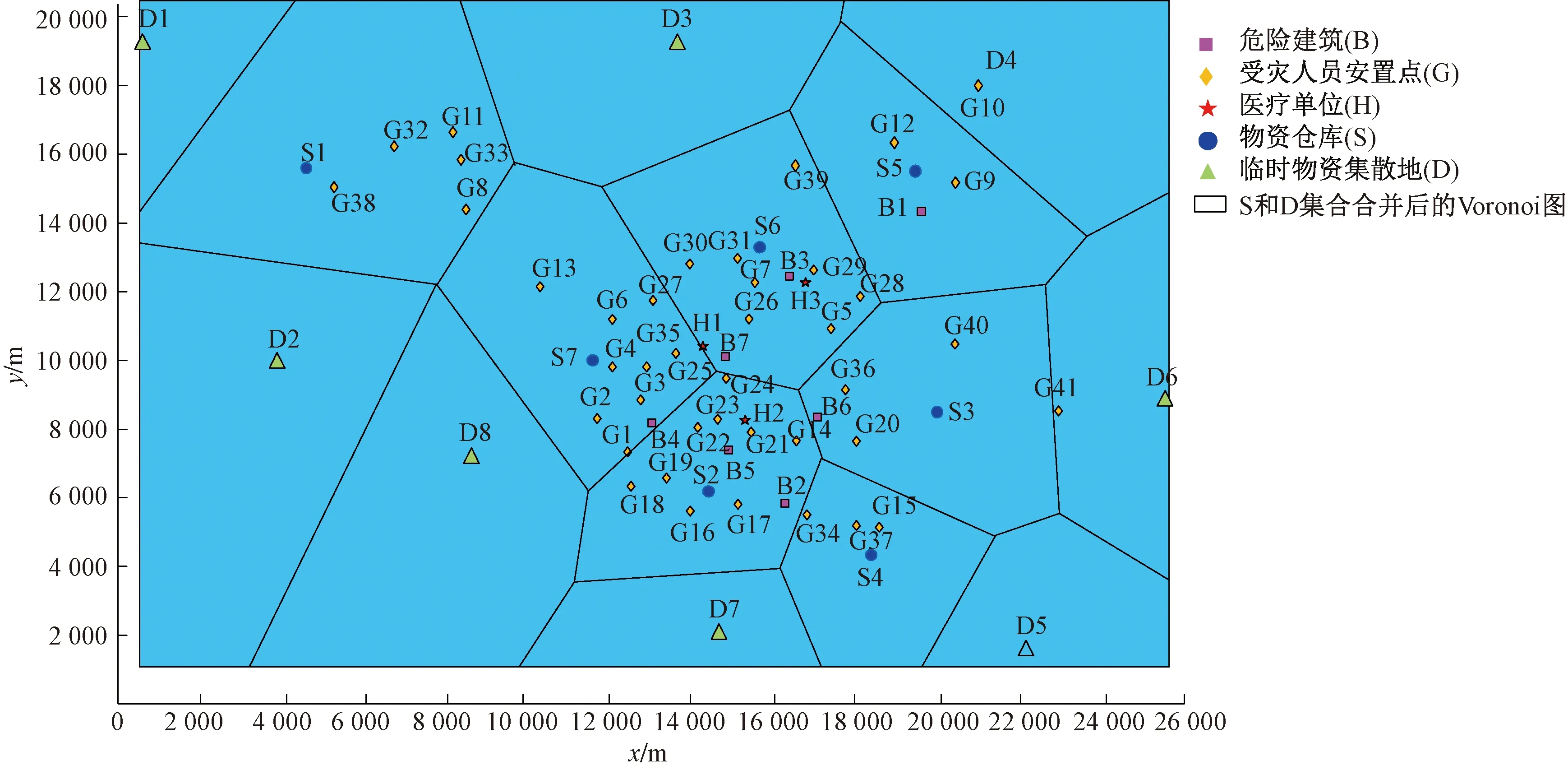
图2 S集合和D集合的三角剖分Voronoi图

根据三角网剖分计算结果,所生成对应的维诺图,可以明确看出,每个S和D负责周边救援点或医院的范围,及数量的构成。这样将整个城市配送模型问题切割,变成每个单独数据集合的解决模型。例如，S1仓库只需负责考虑配送范围内最近的G33、G32、G11、G38和G8的物资输送。这样构建了当前模型位置向量的集合。

S1配送范围集合为{G33, G32, G11, G38, G8};

S2配送范围集合为{H2, G17, G16, G19, G18, G1, G22, G23, G24, G21, G14};

S3配送范围集合为{G41, G40, G36, G20};

S4配送范围集合为{G34, G37, G15, G15, G37, G34};

S5配送范围集合为{G10, G9, G12, G10, S5,G9};

S6配送范围集合为{H1, H3, G39, G29, G7, G30, G3, G28,G5};

S7配送范围集合为{G13, G6, G27, G25, G35, G3, G2, G4}。

此模型问题的分解,有利于优化算法的计算量,建立逻辑的判断。类似于临近搜索的思路,让物资配送模型只考虑最近控制范围的输送。在后期临时集散地建立后,每个向量集合也会产生相应变动。例如，G10将直接由D4负责,而不再归入S5的集合。同理,在远离城市中心的方向,G集合都将逐渐由Di(i=1,2,…,n)负责,而城市原来已有的本地仓库的Si(i=1,2,…,n),越来越向中心方向辐射,只负责市中心区域的物资运输。

3.2 数据更新机制

由于该系统需要动态计算配送路线,数据更新操作可设定30～60 min的时间间隔进行1次更新,主要是对物资的需求更新、车辆运行路径的更新、运载物资数量的更新、仓库物资数量的更新,新增或减少仓库的情况,危险建筑的预警信息更新及危险道路周边道路的路况更新等方面。

常规的静态数据,只能表示道路的宽窄、物资的需求数量,及目的地位置,但是这些数据对于动态变化的救援现场处理是远远不够的。本文中动态数据,考虑了城市道路的变化,而此种变化,不仅仅是规划道路时判断道路是否拥堵、是否耗时,而是这条道路的路边,是否存在危险,并且动态预测,未来是否存在危险,这样能及时规避路线,避免因为建筑或地质等原因,导致的道路通行能力下降,就可以因此规避危险道路,或是冒险走风险最低的道路。

结合救援优先级因子进行估算,紧急时候,有些危险程度低的路段也可尝试通行,平时则尽量避开。而且因为数据是动态发布的,根据动态数据计算的道路通畅度,也是实时更新的,这样导致规划路线,是一直受后台监控,会随着各项参数的动态变化,而实时更新。

对比其他算法,只在发车前考虑道路的远近或路况,发车后遇到特殊情况,无法及时计算新的路线,无法安排新的任务,只能人工解决,本身算法可大大提高处理问题的效率。同时,应对突发的情况和后续救援力量的引入,可提供智能算法支持。现实中救灾点是可能突然变多的,仓库是可能枯竭的,所以分配任务的模式,会考虑这种突发状况,及时变更车辆的运输路线,哪怕运输很少的物资到达新的救灾点,也足以挽救最危险的病人。

随着时间推移,外界救援力量的加入,城市高速路口会建立临时的物资集散地,这里可以认为外界物资供应充足,新的运输车辆也会作为因子加入计算,这是原有车辆的救援重心,就会被算法调整为救援市中心受灾严重地区为主,因为市中心是外界力量能到达最远的地方。整个城市的外围,就不分配本地救灾车辆和仓库,由临时集散地派车救援,而熟悉城市状况的本市人员和车辆,放在了受灾严重城市中心区域进行救援,这种规划使得后期救灾模型,将由内而外的扩展救援力量。

3.3 算法具体实现

通过前面分析,本文中采用强化学习[16-21]对数据进行训练,得出配送规划模型,物资配送规划模型核心就是在确保道路畅通的情况下,找到最短路径,马尔科夫决策过程(Markov decision process, MDP)[22]是一个由4个元素构成的元组(SS,AA,TT,RR),其中SS是一个包含所有状态的有限集合,AA是一个包含所有动作的有限集合,TT是一个定义为TT:SS×AA×SS→[0,1]的转换函数,RR是奖励方程。在计算奖励方程的过程中，自定义4个因子,来计算每种不同规划方案的奖励,通过在配送规划路径中,赋予实际意义,来参与计算。

(1)Z因子为决策价值。根据每次运输物资救援的人数和装车物资包的总数量,Z的计算公式为

Z=M1δ1+M2δ2+…+Miδi,

i=1,2,…,n

(7)

式(7)中：Mi为每次救援物资包的数量，δ为代表权重价值,即根据每个不同物资属性分类,如当前为紧急时刻,那么医疗物资的δ值为1.5,食品生活物资的价值为0.2。而普通时期,δ的价值相等,都是1；而安全时,医疗物资的价值0.8,食品价值1.2。

(2)A因子为单位时间救援人数比。根据单位时间(每小时)计算,每小时运输物资量和救援人数,由于此处考虑了时间,因此会对后面模型中路程的选择产生影响,判断函数决定MDP找到最高效路径的效率。A因子的计算式为

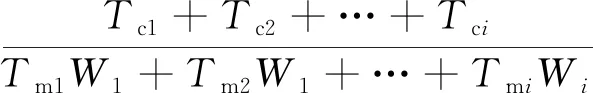
i=1,2,…,n

(8)

式(8)中：Tci为每次运输物资的数量；Tmi为每次汇总的运输时间；Wi为物资权重的总和[见式(1)]。

(3)U因子为救援物资覆盖的人口平均比例。可算出每个救援点,收货物资的人口比例,归纳为一个集合Ut={U1,U2…,Un},用计算基尼系数[23-24]的公式,计算当前集合的分配均衡度。即可得出覆盖率Ur的公式为

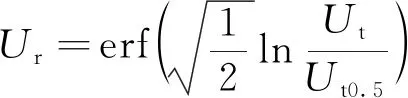
(9)

(4)R因子为运输效率因子。

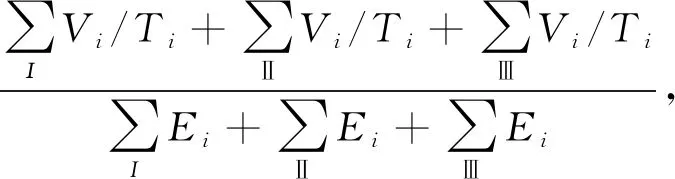
i=0,1,2,…,n

(10)

本文中提出强化学习优化(reinforcement lear-ning optimization,RLO)模型的具体处理流程如下(图3)。

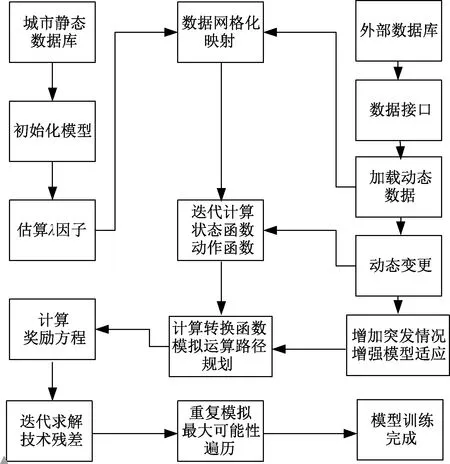
图3 RLO模型处理流程图

(1)初始化静态模型及参数,根据设计的数据库及数据模型,将某测试城市的数据导入。建立对应的城市网格静态信息,如城市的建筑静态信息、道路静态信息、存储物资信息、救援点、储备仓库的静态信息。及前文提到的电力、水利、热力、燃气等数据信息,将城市网格化后的每个点,赋予矢量数据含义。

(2)设置指定的紧急情况因子,此因子λ为人工指定,由现场的危急状况决定,目前分为安全,普通,紧急三种状态,分别应对了不同情况下的应急措施及流程,同时为配送的物资配比,先后逻辑,决定了完全不同的算法逻辑。其中紧急情况下,以救生为主,普通情况下,以正常维持,安全情况下,目的以人群正常生活为主。

(3)实时传输,变化动态数据,将根据卫星、电话、路边监控、其他部门数据库汇总的信息,实时导入当前模型库,主要包括装载车辆上的卫星定位信息,仓库中的物资储量信息,道路拥堵信息,每个安置点的需求物资数量,各个危险建筑的预警信息等。

(4)将所有数据映射到城市网格中,映射数据,将不同意义的矢量数据,映射到城市的每个网格点,而每个车辆信息,及车载货物信息,映射到对应车辆的网格,每个安置点需求物资,映射到安置点的网格,每个危险建筑的预警信息,映射到建筑周边的道路网格。此时的数据及MDP中的状态向量。

(5)根据需求,计算每辆车的装载量,运输路线,采用迭代方法,规划出大量的模型可供选择(最大载重,最大体积和最大数量法),并将物资价值结合救援优先级因子,计算每批次运输的货物最大价值、覆盖率等,即Z、A、U和R四个参数。此时的运输路径,即MDP中的动作函数。

(6)模拟测试,随时更改物资需求、配比、救援优先级因子、物资权重,已经增加新的安置点,新增临时物资集散地,新增外界救援力量,并调整危险建筑的状态,模拟电力、水利、燃气等设施发生危险时候的情况,计算每个道路网格的路口因子β,并归纳路线通畅度C。这里种种条件的设置,增加的是MDP的转换函数,使其可以熟悉各种突发状况。

(7)计算奖励方程,根据Z、A、U和R四个方向,求每种不同规划方案的奖励。并让机器通过计算每个路径网格的实际坐标距离,不仅求解路线的曼哈顿距离,还求出路线的实际运行距离,预估运输时间。

(8)根据奖励方程,迭代求解,使得贝尔曼残差最小化,同时满足价值方程最高,即可以通过此自我验证,自我学习的过程,建立RLO模型,采用MDP方法测试各种震后救援应急状况。

(9)模型模拟连续运转几百小时,遍历所有可能的情况,所有的突发条件,以及所有不同运载运力的变化,使得当前模型的收敛效果好。根据机器性能不同,最终模型效率终能够达到最高,实现了救灾运输高效,覆盖,省时等特点。根据检验模型的分布函数,判断贝尔曼残差最小,当前模型即可认为训练完成。在应急救援早期,外部的救援还无法及时赶到的情况下,通过本地应急物资仓库配送路线如图4所示。

图4 基于物资仓库的配送路径

当救援达到中后期,外地物资源源不断输送,本地物资仓库和外地运送临时物资集散地都可以进行物资配送,通过RLO改进算法优化后得到配送路线如图5所示。

图5 基于物资仓库和临时物资集散地的配送路径

4 实验结果分析

实验测试样本为物资仓库(S)数据共计7个样本点,临时物资集散地数据共计8个样本点,医院数据为3个样本点,受灾人员安置点数据为41个样本点和危险建筑样本点为6个。已知每个点具体坐标,可求出仓库、集散地、医院和安置点之间的曼哈顿距离,根据曼哈顿距离,进行强化学习优化算法训练。强化学习的算法效率主要体现在优化奖励方程,经过若干训练迭代计算后,平均奖励方程结果越大该算法性能越好,因此进行实验对比发现,本文RLO改进算法,在灾情早期的运输效率上,有明显提高,并且能最大价值地配送急需物资,同时提供了对受灾人群的覆盖率,总体上能够解救更多的伤员(表1)。

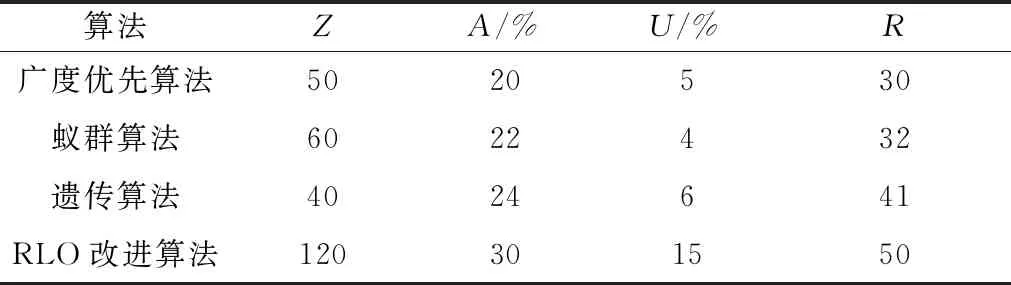
表1 救援初期不同算法4因子数据对比

在救援中期,因为价值因子权重统一,无须判断价值,只考虑救援效率和覆盖率和运输效率时,因为配置模式考虑了动态增加的外界救援力量,及临时物资集散地的模式,所以使得运输力量得到最大程度挖掘,Z、A、U和R因子都有了大幅提高(表2)。

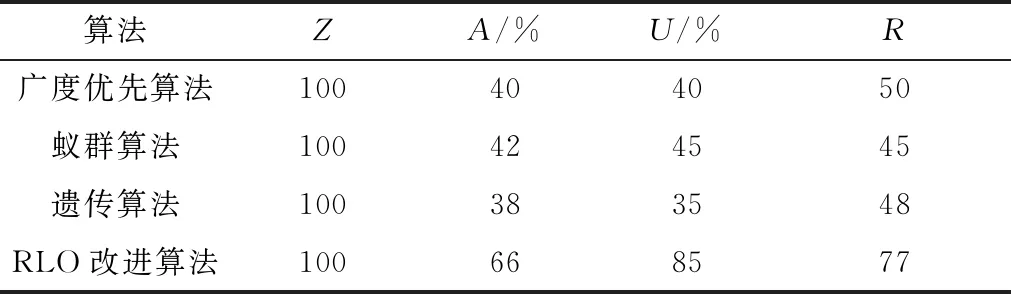
表2 救援中期不同算法4因子数据对比

在救援末期,救援力量大幅提高之后,每种算法的区别并不大,本方法判断价值的A和U因子再次发挥作用,将生活物资的配送力量提高,并最大程度地覆盖了全部受灾人群,而其他两项指标(Z和R因子),比起同类算法,提高幅度并不明显(表3)。

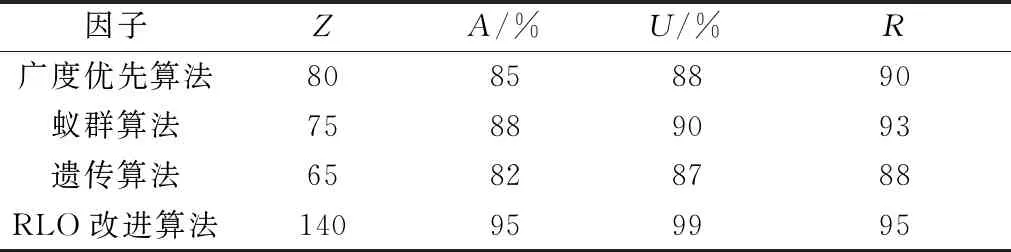
表3 救援末期不同算法4因子数据对比

5 结论

本算法模型,在重大地震灾害发生时,产生的救援规划方案,救援组织能力,对比其他方法,得到了巨大提升,具体得到以下结论。

(1)采用事先训练好的强化学习模型优化,可以提前演练可能出现的种种临时状况,让AI学会不同情况的应对,真正需要计算的时候,只需要带人数据,快速求解即可。

(2)通过引入救援优先级因子λ,物资权重因子δ等判断条件,结合Z、A、U和R四大价值模型的函数,使得救援方案,实现了高效快速地运输最急需物资,运输覆盖人群高,覆盖城市救灾点的范围最高。

(3)本算法不同于常规方法,只考虑路程的远近,线路的通畅及运输过程的时间是否最短,是否最高效。而是从实际情况出发,运输的过程,不是目的,目的是尽早让更多的受灾群众,收到物资获得救助。而不是以送达为终端目标。现实的生活中,货物送达即为达标,货物之后的使用效能,不在考虑范围,而以本文逻辑,尽量让物资的覆盖率提高,让有价值的物资优先配送,让单位时间获救人数最高,同时兼顾运输效率,才是该配送方案优化的核心思想。

(4)应急救援,效率优先,同时还要考虑到人员使用物资的效果,物资消耗有时间长度,所以覆盖率和单位时间人数比的两个奖励函数,对本算法有核心意义。不采用平均数算法,只送一个救灾点,完全救助,但是其他地点苦等不至,大量伤亡产生,在最后汇总的数据中,是体现不出来的,都是一个获救人数除以总人数的比例,但是现实中,如果能均衡调配,让每个地方都获得一部分物资,就能先救治最危重的伤病员,尽可能提高前期获救人数的覆盖范围,从另一个角度,提高了物资运输效率,真正提高了运输效率,进行更有效的救援。

(5)采用对每个建筑物的网格化管理,通过各个部门的综合数据警示,提前预警即将发生危险的建筑位置,及受影响的道路,为规避危险路线,合理安排运输路径,提供了数据支撑。也为突发情况,提供了算法方向的预先设计,提前模拟特殊情况的发生,为真正情况下的反应,提供了算法基础。

(6)加入各种动态数据,如外围临时集散地的建立,为整个数据的漩涡式模型配送,提供了数据支撑,救援永远是从外向内的,外围的数据加入,更使得原有奔波于市中心和市郊区的运输车队,全力以赴,集中到市中心的救援,而外围市郊的救援规划,交给了外界救援力量。这样就更加合理的安排了运输路线,更快地实现对全市的救援覆盖。