电网不平衡时电流限制的风电并网变流器功率/电流灵活控制

赵晨聪， 刘军， 谢宙桦

(1.西安理工大学 自动化与信息工程学院，陕西 西安 710048； 2.西安热工研究院有限公司，陕西 西安 710054)

0 引 言

随着环境问题和能源危机的日益严重，世界各国均已经在新能源领域展开战略部署。由于风电具有资源丰富、产业基础好、环境影响小等优势，我国的风力发电技术发展非常迅猛，累计风电并网容量已达1.8亿千瓦。并网变流器作为直驱式永磁风电系统的并网接口，在并网控制中起着举足轻重的作用[1-2]。然而，并网变流器的运行性能易受电网电压的影响，大功率单相负载的介入、单相负载在电网中的不平衡分配以及单相负载用电的随机性等因素都会造成电网不平衡[3-4]。电网电压的不平衡会导致并网功率波动，并网电流畸变，以及并网过电流等问题，给系统的运行带来安全隐患，甚至会引起并网变流器的过电流保护动作[5-6]。文献[7-9]针对输出功率波动以及电流畸变的问题，采用双电流环矢量控制的方法，实现了输出功率恒定、电流平衡且正弦化的目标，但采用该控制策略下的输出电流峰值远大于额定值。文献[10-12]虽然同时抑制了输出有功和无功功率的波动，但是却以电流的严重畸变为代价。文献[13-14]引入了权重系数的思想，将抑制有功功率波动、抑制无功功率波动及抑制负序电流分量这三种控制方式下的电流参考表达式进行了整合统一，实现了功率和电流的协调控制，但该控制策略所需控制器数量较多，参数整定不易实现，而且电流峰值过大的问题未被解决。文献[15]分析了输出功率波动以及电流谐波产生的原因，并进行了量化分析。该控制方案利用加权的思想实现了输出功率和电流的协调控制。然而，该方案无法实现电流平衡控制。此外，在控制过程中还需要额外的采用陷波器。文献[16]虽然也通过引入权重系数的方法来实现输出功率和电流的协调控制，但该方案采用的LCL滤波器本身具有较好的谐波抑制能力，因此不能完全证明该控制策略在调节谐波能力上的优越性，此外，该控制方案下的并网电流幅值越限。以上所述控制策略均以抑制输出有功功率波动、无功功率波动及电流平衡为主要目标进行控制的，不平衡电网电压导致的输出电流过大的问题未被解决。为了保证并网变流器的安全运行，三相输出电流必须被控制在安全的范围内。文献[17]在解决并网过电流问题的基础上，分析了有功功率和无功功率参考值的解析表达式，实现了有功功率的恒定控制，但并网电流的不平衡程度加剧。文献[18-19]基于坐标旋转变化得出了正、负序电流的参考值，提出了dq坐标系下的限流控制方案。但该控制方案实现过程较为复杂，并且不能实现有功和无功功率的灵活控制。因此，不平衡电网电压下如何在并网功率/电流灵活控制的基础上解决过电流问题有待进一步的研究。

本文基于瞬时功率控制以及电流平衡控制，分析不平衡电网电压下造成风电并网变流器输出功率波动、输出电流过大及畸变的原因。着重研究瞬时功率控制以及电流平衡控制下三相输出电流的最大峰值，并用于指导功率参考值的设定。同时，根据电流参考值间的本质联系，提出功率/电流灵活控制的方法，在限流基础上实现风电并网变流器功率/电流的灵活控制。

1 并网变流器结构

直驱式永磁风电系统通常采用双PWM变流器结构，其并网变流器的主电路拓扑结构如图1所示。图中：uga、ugb、ugc分别为电网相电压；uca、ucb、ucc分别为变流器端电压；L为电抗器电感；R为电抗器内阻；udc为直流侧电压。

图1 并网变流器结构图Fig.1 Structure diagram of grid-connected converter

在电网电压不平衡情况下，根据对称分量法可将电压分解为正序分量、负序分量和零序分量，但对于三相三线制系统，无零序分量的流通路径，所以不平衡电网电压可表示为

(1)

式中：U+和U-分别表示正序和负序电压的幅值；θ+和θ-分别表示正序和负序分量的初始相位；ω表示电网频率。

将三相电网电压进行Clarke坐标变换到两相αβ静止坐标系下，则有

(2)

式中：

2 峰值电流分析

2.1 瞬时功率控制

根据瞬时功率理论，输出功率可表示为

(3)

式中iα和iβ分别为αβ坐标系下的电流分量。

根据式(3)，可求出在给定有功功率P*和无功功率Q*下的电流值为

(4)

将式(4)进行化简整理，可得出瞬时功率控制下的电流参考值为

(5)

式中iαgl(p)、iβgl(p)及iαgl(q)、iβgl(q)分别为瞬时功率控制下的有功电流分量及无功电流分量。

将式(2)代入式(5)中，可得式(5)的分母项为

U+2+U-2-2U+U-cos(2ωt+θ++θ-)。

(6)

在电网电压不平衡情况下U-≠0，因此，电流参考值中存在2U+U-cos(2ωt+θ++θ-)项，这将导致采用该控制策略时电流中存在大量的谐波分量。

将式(5)进行Clarke反变换，可得出三相输出电流参考值为

(7)

其中：

进而可得，三相电流峰值为

(8)

因此，瞬时功率控制下的三相电流最大峰值为

(9)

若电网是理想的三相平衡状态，则U-=0, 三相电流最大峰值可表示为

(10)

(11)

2.2 电流平衡控制

为了保证输出电流平衡，必须消除系统中的负序电流分量，根据式(4)可求出电流平衡控制下的电流参考值为

(12)

式中iαdl(p)、iβdl(p)及iαdl(q)、iβdl(q)分别为电流平衡控制下的有功电流分量和无功电流分量。

由式(12)可知，在电流平衡控制策略下，电流参考值中不含有谐波项，因此采用该控制策略可得到平衡且正弦的三相输出电流。在电压不平衡情况下，由于系统中仍存在负序电压分量，负序电压分量与正序电流分量相互作用，这将导致输出有功和无功功率存在波动。

电流平衡控制下的三相输出电流参考值为

(13)

其中：

水库所在区属中低山丘陵地貌，坝址地处河谷上段较为狭窄的地带，呈U字形，左右两岸均属土质边坡，左右岸山坡坡度约15°～40°。该坝体填土层的渗透性弱，大坝基础为强—弱风化白云岩，左右两坝肩表部为残坡积层，坝址范围内未发现有影响大坝稳定的地质作用，大坝基础相对较稳定。根据 《中国地震动参数区划图》，工程区的地震动峰值加速度为0.15 g，地震动反应谱特征周期为0.45 s，相应地震烈度为Ⅶ度。

采用该控制策略下的输出电流平衡且无畸变，三相输出电流的最大峰值为

(14)

2.3 电流峰值控制

通过以上分析可知，在电网电压不平衡情况下采用瞬时功率控制以及电流平衡控制下的输出电流幅值均高于理想电网下的并网电流幅值。过大的并网电流会给系统的正常运行带来安全隐患，甚至烧毁开关器件。因此，电流峰值的控制问题不容忽视。由式(9)及式(14)可知，电流的最大峰值取决于输出有功功率、无功功率以及正负序电压分量。正负序电压分量是由不平衡电网本身决定的。因此，为了降低电流峰值，可通过控制有功功率及无功功率来实现。设定并网变流器输出电流的允许最大峰值为Imax，根据式(9)及式(14)可知，在电流峰值允许范围内，系统的输出有功功率及无功功率应满足

(15)

在电网电压不平衡情况下，风电系统不仅应具备并网规范中要求的不脱网运行而且应该向主网提供一定的无功功率支撑。根据电网规范，风电场向电网注入的无功电流可表示为

Iq≥1.5×(0.9-Ug)IN。

(16)

式中：Ug为并网电压的标幺值；IN为额定电流。

结合式(15)及式(16)可知，在对不平衡电网进行无功支撑的同时保证逆变器在最大允许峰值电流下运行，有功和无功功率可表示为：

(17)

因此，为了保证输出并网电流始终在安全范围内，可灵活控制输出有功功率和无功功率如下：

(18)

当电网电压平衡时，设置开关信号S=0，系统输出有功功率及无功功率参考值为理想电网下的输出功率Pzc、Qzc。当电网电压不平衡时，开关信号S=1，系统输出有功功率及无功功率参考值为考虑电流限制下的输出功率Pxz、Qxz。

3 不平衡电网下功率/电流灵活控制

3.1 功率/电流灵活控制

(19)

瞬时功率控制下的电流参考值不仅存在基波分量还存在谐波分量。电流谐波分量主要以3次、5次、7次等低次谐波为主，该谐波分量的大小将对输出功率波动的抑制程度及三相电流的平衡度产生影响。因此，为了实现功率和电流的灵活控制，可通过调节并网电流中的谐波含量来实现。

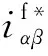
(20)

(21)

图2 系统控制结构图Fig.2 System control structure diagram

3.2 控制策略性能分析

由于所提控制策略需要分别对电流基波及谐波分量进行控制，为了避免正负序电流的分离及复杂的坐标变换，采用比例复数积分(proportional complex integral，PCI)控制器在αβ坐标系下实现对电流的控制[20]。

PCI控制器的传递函数为

(22)

式中：Kp、Ki分别为比例和积分系数；ω为基波角频率。该控制器存在复数j，不易实现。根据复变函数理论可知，j代表幅值不变，相位移90°。由于在αβ坐标系中存在正交关系mα=jmβ，因此，该复数域控制器可由图3所示结构实现。

图3 PCI控制结构图Fig.3 PCI control structure diagram

图4为PCI控制器的Bode图。由该图可看出，该控制器在电网频率50 Hz处有无限大增益，而在其余频率段内几乎无增益，因此该控制器可实现对电流基波分量的无差跟踪控制。

图4 Gf(s)Bode图Fig.4 Bode diagram of Gf(s)

在电流内环中不仅需要对电流基波分量进行控制，还需对谐波电流进行有效控制。基于PCI控制器，提出了比例多重复数积分控制(proportional multiple complex integral，PMCI)对电流谐波分量进行控制。PMCI控制器的传递函数为

(23)

图5为PMCI控制器Bode图。由图可看出，在3次、5次、7次谐波频率处的增益很大，而在其余频段处，增益均未有明显增大，因此采用该控制器可以对电流低次谐波分量进行有效控制。

图5 Gh(s)Bode图Fig.5 Bode diagram of Gh(s)

根据本文所提控制方案，电流内环控制结构如图6所示。图中Gf(s)和Gh(s)分别为基波及谐波控制器的传递函数，KPWM为PWM变流器的等效增益，通常取KPWM=Udc/2，Ug为电网电压。

图6 电流内环控制框图Fig.6 Control block diagram of current inner loop

根据图6，可得系统输出电流为

Xu(s)Ug(s)，

(24)

(25)

其中：Xf(s)表示输出电流和电流基波分量参考值间的传递函数；Xh(s)表示输出电流和电流谐波分量参考值间的传递函数；Xu(s)表示输出电流和电网电压间的传递函数。

表1所示为系统网侧的主要参数，根据表1可得Xf(s)、Xh(s)及Xu(s)的Bode图，分别如图7～图9所示。

表1 仿真模型的参数

图7 Xf(s)Bode图Fig.7 Bode diagram of Xf(s)

图8 Xh(s)Bode图Fig.8 Bode diagram of Xh(s)

图9 Xu(s)Bode图Fig.9 Bode diagram of Xu(s)

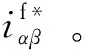
图9所示为Xu(s)的幅频和相频曲线。由于电网电压相当于一个扰动分量，Xu(s)在电网基波频率50 Hz处及3次、5次、7次谐波频率处的增益均很小，因此，电网电压对并网电流的扰动影响可忽略不计。

4 仿真分析

在不平衡电网电压下，为了验证所提控制方案的有效性及优越性，基于MATLAB/Simulink对并网变流器的控制进行仿真。模拟了两类电网电压不平衡的情况。第一类不平衡情况以A相电压的瞬时跌落为例，在0.1 s时A相电压跌落30%，在0.5 s时又恢复至正常水平。第二类不平衡情况以A相发生单相短路接地故障为例对所提控制策略进行仿真验证。

图10所示为在两类不平衡电压情况下未考虑限流时瞬时功率控制及电流平衡控制的仿真结果。由图可看出，在两类不平衡电压下采用瞬时功率控制时输出有功和无功功率基本保持恒定，但并网电流失真严重，谐波畸变率较大，以A相电流为例，谐波畸变率分别达到了11.34%及35.53%。电压不平衡期间的输出电流明显高于理想电网下的电流峰值。在两类不平衡电压下采用电流平衡控制时的三相电流平衡度较高，A相电流谐波畸变率仅有1.39%及3.25%，但输出电流峰值明显高于变流器所允许的最大电流峰值，并且系统的输出有功和无功功率均存在明显的波动。

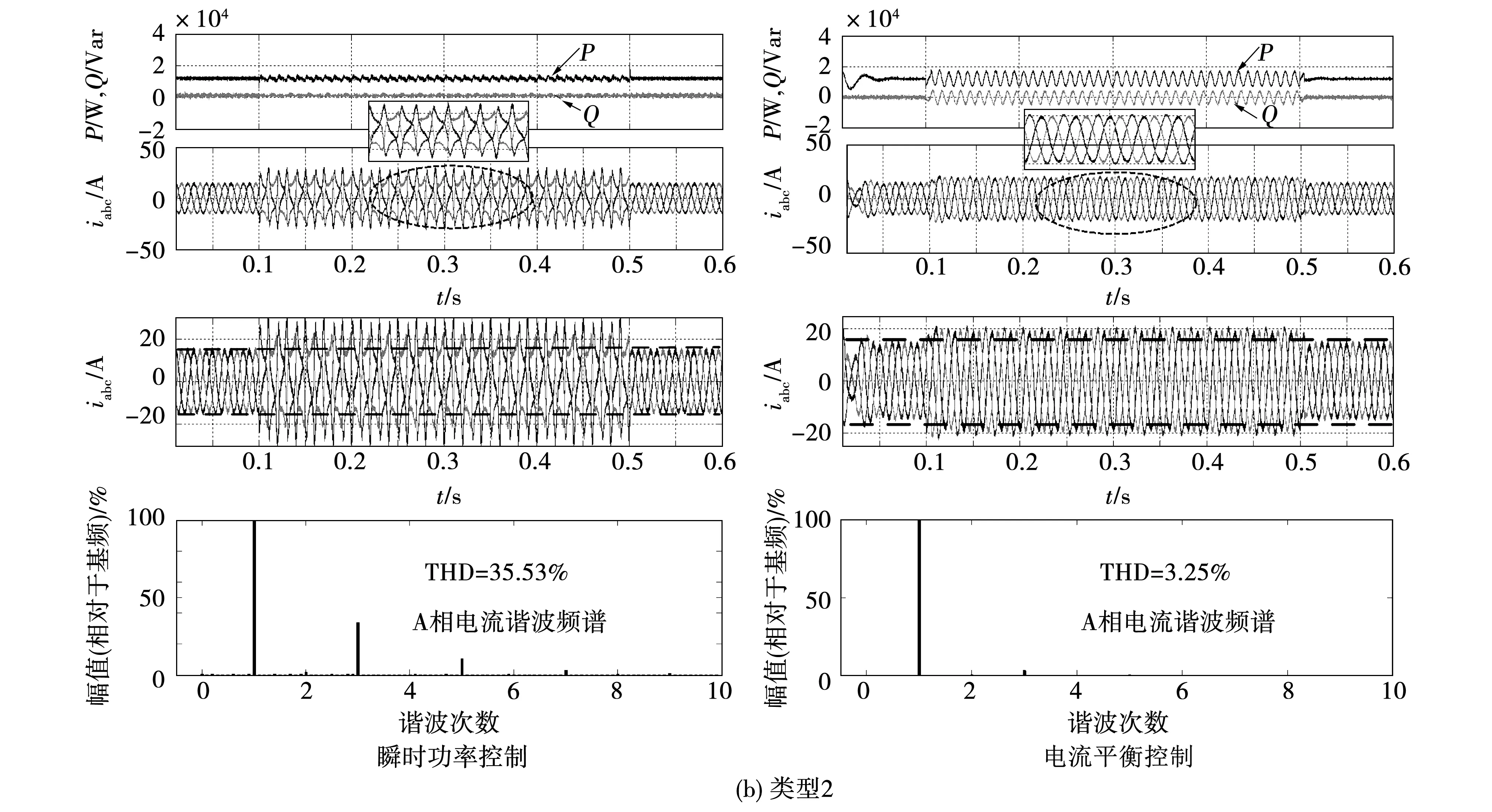
图10 两类不平衡电网电压下瞬时功率控制及电流平衡控制仿真结果Fig.10 Simulation results of instantaneous power and current balance control under unbalanced grid voltages

图11所示为两类不平衡电压情况下考虑限流时瞬时功率控制及电流平衡控制的仿真结果。由图可看出，在不平衡电压下采用瞬时功率控制时系统输出功率几乎趋于恒定，虽然电流失真，但其幅值被限制在安全的运行范围内。采用电流平衡控制时虽然功率存在波动，但三相输出电流不仅平衡且正弦度较高，幅值始终控制在最大电流允许的范围内。

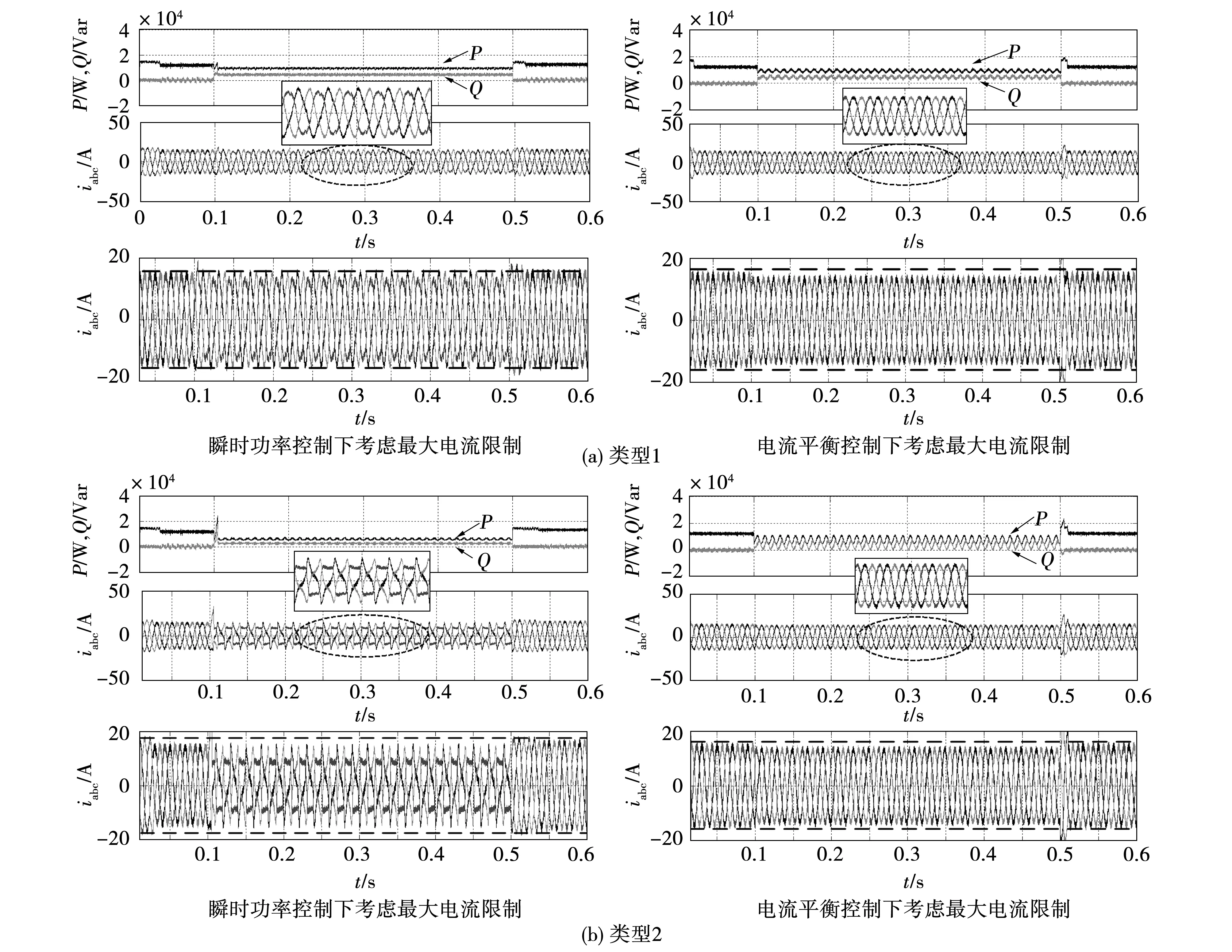
图11 考虑最大电流限制的两种控制策略在两类不平衡电压下的仿真结果Fig.11 Simulation results of two control strategies considering current limiting under unbalanced voltage

图12所示为在两类不平衡电网电压情况下采用文献[15]所提协调控制策略的仿真结果。该控制方案为了实现功率及电流的协调控制，在电流参考计算中引入了调节系数k，但与此同时，陷波器也被引入用于控制方案的实现。由图12可看出，在两类不平衡电压下，当k=0时，系统输出电流的正弦度较好，谐波畸变率较低，分别为4.20%及4.93%，但三相输出电流并没有达到三相平衡的状态并且输出功率波动较大。当0

图12 两类不平衡电网电压下采用文献[15]所提控制策略的仿真结果Fig.12 Simulation results of control strategy proposed in reference [15] under two kinds of unbalanced voltages

图13所示为在两类不平衡电网电压情况下采用本文所提控制策略的仿真结果。在0.1 s～0.2 s阶段，权值系数k=0，由图可以看出，在此阶段，输出功率波动较明显。然而，三相电流是平衡且正弦的。通过对A相电流的谐波频谱分析可知，总谐波电流畸变率较小(即类型1：THD=3.89%，类型2：THD=4.49%)，并且其中低次谐波占比很少，这与理论分析相一致。在0.4 s～0.5 s阶段，k=1，该阶段相当于瞬时功率控制，输出有功和无功功率恒定，但三相并网电流畸变严重(类型1：THD=7.96%，类型2：THD=21.34%)。在0.2 s～0.4 s阶段，随着k值的增大，输出功率的波动逐渐减小，电流不平衡度和电流畸变度逐渐增大。根据图中的电流曲线可知，在电网电压不平衡期间，最大电流峰值始终被控制在并网变流器所允许的安全范围内。仿真结果表明了该控制方案可以在限流的基础上实现并网功率及电流的灵活控制。

图13 两类不平衡电网电压下采用本文所提控制策略的仿真结果Fig.13 Simulation results of the proposed control strategy under two kinds of unbalanced voltages

基于以上理论及仿真分析，现将各类控制方案的控制效果总结如表2所示。瞬时功率控制只能实现功率恒定，电流平衡控制只能实现电流平衡正弦化。文献[15]所提方案虽然通过调节系数可以实现输出功率恒定及电流正弦化，但其无法实现三相并网电流的平衡，峰值电流过大的问题也未被解决。而本文所提控制策略不仅可以通过调节系数实现功率及电流的多目标控制，而且还解决了不平衡电网电压下过电流的问题。

表2 不同控制策略下的效果对比

为了进一步分析控制策略的控制性能问题，将文献[15]所提协调控制策略与本文所提控制策略进行量化对比如表3所示。由表3可知，采用本文所提控制策略下的电流谐波畸变率和文献[15]所提的控制相比均有所减小。此外，虽然在k=1情况下采用所提控制方案的输出功率波动稍大于文献[15]所提控制，但是在整个控制中的输出功率波动最大值较文献[15]有所减小。

表3 不同电压类型下的控制性能对比

5 结 论

为了解决电网电压不平衡情况下输出功率波动、并网过电流及电流畸变等问题，提出了一种考虑限流的并网功率/电流灵活控制方案。本文的主要贡献包括以下几个方面：通过控制输出有功和无功功率，进而保证三相电流在安全范围内；在电流参考值中引入权重系数，无需检测谐波分量即可实现功率及电流的灵活控制；对三相并网电流的控制是在αβ坐标系下实现的，无需电流正负序分离和复杂的旋转坐标变换，结构简单；在电网电压不平衡情况下可以为电网提供一定的无功功率支撑。