永磁同步电机模糊代价函数预测转矩控制

史涔溦， 马红如， 陈卓易， 邱建琪

(1.浙江大学 电气工程学院，浙江 杭州 310027； 2.浙大宁波理工学院 信息科学与工程学院，浙江 宁波 315100)

0 引 言

在现代交流伺服系统中，永磁同步电机(permanent magnet synchronous machine, PMSM)广泛应用在工业自动化、航空航天和工业机器人等领域[1]。PMSM的两种主要控制策略是磁场定向控制(field-oriented control, FOC)和直接转矩控制(direct torque control, DTC)。直接转矩控制方法瞬态转矩响应快、电机参数依赖性小、控制结构简单[2]，然而，传统的直接转矩控制采用两个滞回比较器，通过查表选择电压矢量，造成转矩和磁链脉动大[3]。为了实现更精确的控制和更高的性能表现，有限集模型预测转矩控制(finite control set model predictive torque control, FCS-MPTC)吸引了很多研究者们的关注[4]。有限集模型预测控制基于功率逆变器有限数量的开关状态，仅对可能的电压矢量进行遍历，选择使代价函数值最小的电压矢量，直接将其开关信号输出给逆变器。

有限集模型预测可以在一个代价函数中包含多个控制目标，比如电流、转矩、磁链、有功功率、开关次数、共模电压和无功功率等。根据不同的控制目标，可以将这些代价函数分成三类[5]，第一类是没有权重系数的代价函数：这类代价函数只约束了一个或一种变量。由于代价函数中所有项具有相同的单位和数量级，所以不需要加权因子，例如电流模型预测代价函数中对电机定子电流的控制[6]；第二类是包含主要控制目标和次要约束条件的代价函数。其主要控制目标是为了使系统按照给定的参考值变化，次要约束条件是为了优化系统的性能表现，通常是为了降低开关频率、共模电压和无功功率等，这一项前面需要加权因子来调节。第三类代价函数中的各项具有同等重要性。因为各控制目标的量纲不同，也需要权重系数进行调整。FCS-MPTC中控制目标转矩和磁链就是第三种情况。

权重系数的大小反映了这一项在系统控制中的重要程度，也会影响到系统的动态响应和稳态误差。如果权重系数设置得不合理，就达不到预期的控制效果，甚至会使系统出现震荡。为了解决这一问题，除了经过实验逐步调整权重系数[7]，一些学者设计采用消除权重系数的代价函数，将对转矩和磁链的控制，转化为对定子磁链矢量的控制[8]或是采用电压代价函数[9]，文献[10]采用相对误差率的方式，将转矩与磁链统一到了同一量纲，进而取消了权重系数。但是这些方法在去掉权重系数后，又增加了电机预测模型的计算量。有的文章采用模糊控制调整权重系数，例如文献[11]在电流模型预测中调节电流和开关次数的权重系数，但是实验结果中又缺乏表征开关频率的相关量。文献[12-13]设计了不同的模糊规则优化了直接转矩模型预测中开关次数的权重系数，主要是降低了开关频率，而在转矩预测中主要控制目标是转矩和磁链，开关频率属于次要约束条件。文献[14]在表贴式永磁同步电机的转矩预测中分别根据磁链误差和转矩误差调节磁链和转矩前面的权重因子，但是却只测得了转速波形，并没有观测控制目标转矩和磁链。还有研究采用数值计算的方法，通过计算得到权重系数的值，文献[2]根据感应电机转矩纹波和电压矢量之间的数量关系得到了权重系数，但是该方法计算复杂，而且在某种程度上削弱了磁链的重要性。文献[3]由PMSM稳态时转矩和磁链的表达式，推导出了只和电机参数有关的权重系数，但是它的推导是基于表贴式PMSM，内置式永磁同步电机并不适用。

本文将内置式永磁同步电机作为控制对象，在FCS-MPTC系统中，选择磁链与转矩作为代价函数的控制目标，以定子d-q轴电流为输入量，提出了模糊调节权重系数的模型预测控制方法，并与常规代价函数和无权重系数的代价函数进行比较，仿真和实验结果证明了该方法具有更好的控制性能。

1 永磁同步电机模型预测转矩控制

1.1 PMSM数学模型

不考虑铁心饱和、涡流和磁滞损耗，设电机中的电流为三相对称正弦波电流，在d-q同步旋转坐标系下，内置式永磁同步电机的电压方程为：

(1)

定子磁链方程满足：

(2)

电磁转矩方程为

(3)

式中：Ld、Lq为d、q轴电感；Rs为定子电阻；ψf为永磁体磁链；pn为极对数；ωe为电角速度；Te为电磁转矩；ud、uq、id、iq、ψd、ψq分别为d、q轴定子电压、定子电流和定子磁链。

1.2 有限集直接转矩预测模型

在转矩预测中，需要对电机的连续状态方程进行离散化，一般使用前向欧拉法，即

(4)

式中Ts为采样周期。当开关频率比较高时，转子转速、电感、电阻等参数在一个采样周期内近似不变，选择定子电流为状态变量，根据式(1)和式(2)，结合式(4)，由当前时刻的电流、电压和电角速度可得到k+1时刻的电流预测方程为：

(5)

进而得到k+1时刻的磁链和转矩方程为：

(6)

(7)

在理想情况下，数据的采样和控制输出可以同时完成。但是，实际中应用的单片机等数据处理器进行运算需要一定时间，根据k时刻采样的电流计算得到的k+1时刻的最优控制电压矢量不能立即应用。目前，采用的延时补偿方法一般是提前两步预测，即在k时刻预测出k+2时刻的系统状态。

整体MPTC控制原理框图如图1所示。

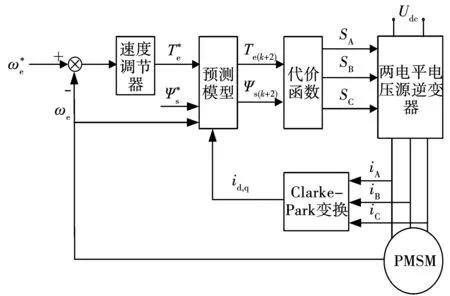
图1 永磁同步电机直接转矩预测模型控制框图Fig.1 MPTC system of PMSM

2 代价函数分析

2.1 代价函数的设计

模型预测能凭借单一的代价函数对多个目标进行控制，因为代价函数中的权重系数可以协调不同单位、幅度和优先级。通过设置变量前面权重因子的比例，就能达到我们想要的控制效果。在传统的电流模型预测中，控制目标一般为id、iq，而电流是同一量纲，在控制中具有同等的重要性，一般在代价函数中不需要再设计权重系数。直接转矩模型预测的目的是对电磁转矩和电机磁链进行控制。对于同一个电压矢量，电磁转矩和磁链表现出的敏感程度不同，反映出的变化快慢和幅值增减各有差异，需要权重系数对这两个变量进行制衡。因此选择代价函数为

i=1,2，…，m。

(8)

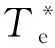
2.2 恒定权重系数的代价函数对控制系统的影响

根据图1控制框图，在MATLAB/Simulink中搭建永磁同步电机直接转矩预测系统模型，仿真中的电机参数如表1所示，直流母线电压Udc=30 V，磁链为给定幅值0.21 Wb，控制周期Ts=50 μs。

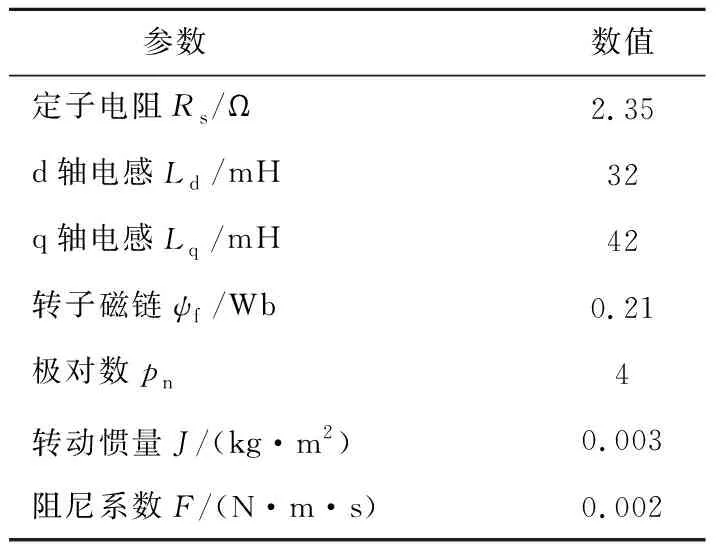
表1 PMSM主要参数

仿真中，速度参考值为120 r/min，电机空载起动，为了直观明显地对比权重系数的影响，式(8)的λ选择1、30这两个数值进行分析。

计算电机电磁转矩与给定值的误差，以及磁链与给定值的误差，可得到图2中的结果。

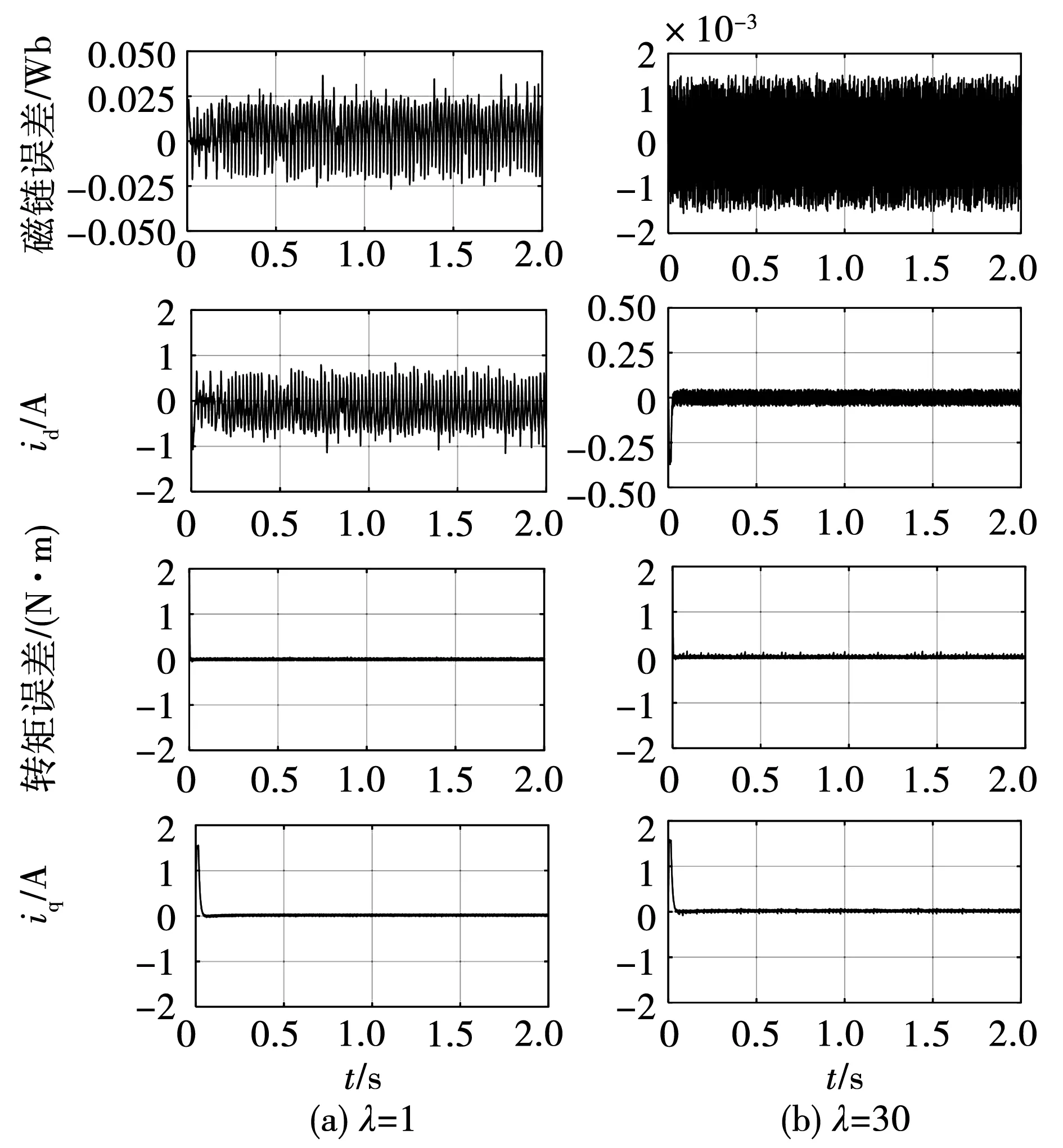
图2 空载启动过程中的磁链转矩误差和dq轴电流Fig.2 Flux linkage error,torque error,id,iq without load

从图2中可以看出，在λ=1时的磁链误差明显大于λ=30时的磁链误差，但是它的转矩波动小，这是因为λ越小，对磁链的偏重程度越低。同时还发现id的变化趋势和磁链误差的变化相近，当磁链误差大时，id的波动幅度越大；iq的变化趋势和转矩误差的变化趋势相近，转矩波动小时，iq波动幅度也越小。

在第7 s时突然增加0.7 N·m负载。图3为加载过程中磁链转矩误差大小比较和d、q轴电流，两种权重系数下磁链与转矩误差情况和空载时大致相同，符合λ越小，磁链误差越大、转矩误差越小的规律。只是在突增负载后，λ=30时转矩误差更为明显，从图3(b)中可以看到，在转矩出现脉动时，相应地iq也呈现出相同规律的波动，而id在负载增加后略下降，然后保持不变。λ=1时，因为id原本的波动幅度就大，在增加负载后id没有太大变化。

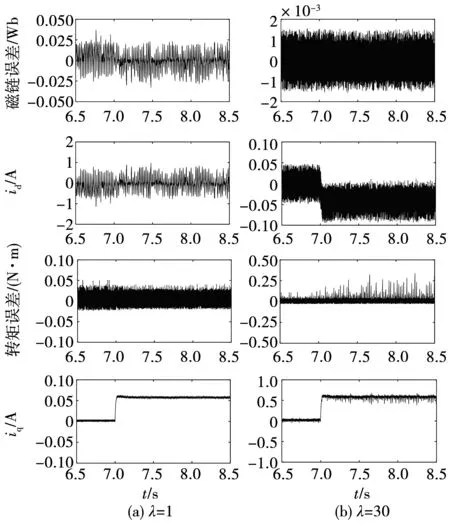
图3 加载过程中的磁链转矩误差和dq轴电流Fig.3 Flux linkage error,torque error,id,iq with load

3 模糊调节权重系数的代价函数

3.1 权重系数的模糊调节

在前文中分析了取不同权重系数的代价函数对系统中磁链误差、转矩误差的影响，以及dq轴电流在空载和带载时的变化。定子dq轴电流的改变在某种程度上反映了磁链和转矩的变化，考虑根据dq轴电流来调节权重系数，这可以用模糊控制的方式来实现，因为模糊控制不必知道控制对象的精确数学表达式，就可以描述输出量与输入量的关系。

本文选择模糊控制系统的输入量为id和iq，输出量为权重系数λ。经过仿真的调试，选定id的实际论域为[-0.6 0.2] A，分为4个子集{A,B,C,D}；iq的实际论域为[-0.1 1.7] A，分为6个子集{a,b,c,d,e,f}；λ的实际论域是[6 20]，分成7个子集{F1,F2,F3,F4,F5,F6,F7}。它们的隶属度函数图像如图4、图5、图6所示。

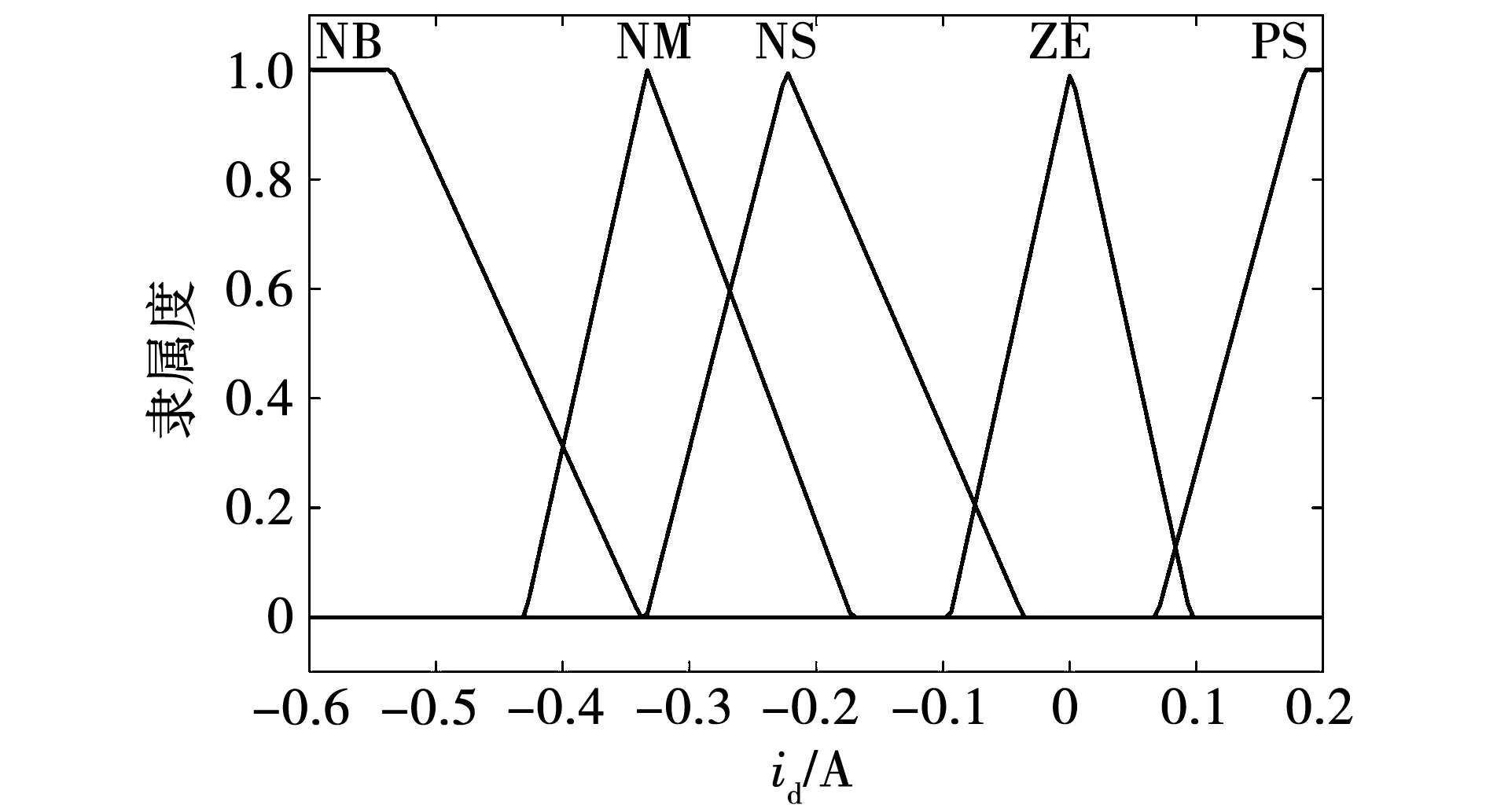
图4 d轴电流的隶属度函数Fig.4 Membership function of id

图5 q轴电流的隶属度函数Fig.5 Membership function of iq

图6 权重系数的隶属度函数Fig.6 Membership function of weighting factors

空载时，转矩为0，iq亦是，转矩脉动比较小。此时主要使磁链接近于给定值，权重系数取一个比较小的值就可使磁链误差控制在一定范围内。电机带负载后，转矩增加，iq增加，id小幅度下降。因为负载前后磁链误差的变化不大，之前的权重系数较小，这时可以适当增加权重系数减小磁链误差。权重系数也不宜过大，否则转矩可能出现明显波动。

为兼顾磁链与转矩，结合id、iq的变化，制定出的模糊规则如表2所示，模糊规则的曲面如图7所示，用重心法解模糊得到权重系数。最后将模糊控制工具箱的输入量和输出量数据生成模糊控制离线查询表，这样在电机控制过程中就不用再进行计算，由采样得到的电流就可以查询到相应权重系数的值。

表2 模糊规则表

图7 模糊规则曲面Fig.7 Surface of fuzzy logic designer

3.2 仿真验证

为了避免权重系数的调节，有的文章中采用相对误差的方法来设定代价函数[10]，即

(9)

式中计算了转矩误差、磁链误差占给定值的比率，因此消除了转矩和磁链这两个单位不统一的情况，在代价函数中去掉了权重系数。

在MPTC中加入模糊控制环节，其它仿真情况和论文第二部分相同。常规代价函数中选择λ=26，将由模糊控制调节权重系数的方法，和常规代价函数(λ=26)以及式(9)作为价值函数的方法作比较，电机空载起动和加载后的情况分别如图8、图9、图10所示。

在图8中，直接转矩预测采用常规代价函数，电机加载后转矩有较大的纹波，磁链保持在给定值0.21 Wb。图9是无权重系数的转矩预测控制，转矩脉动较小，但是磁链幅值波动大。引入模糊控制后，图10中电机的转矩脉动很小，并且磁链幅值波动也小。

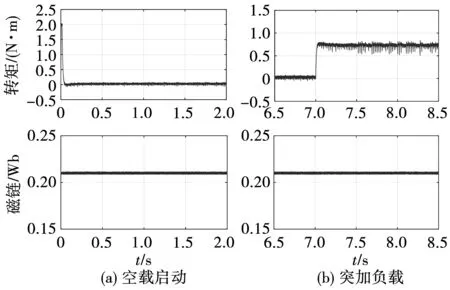
图8 常规代价函数MPTC的控制性能Fig.8 Control performance of MPTC whose cost function is conventional

图9 无权重系数代价函数的控制性能Fig.9 Control performance of MPTC whose cost function has no weight coefficient

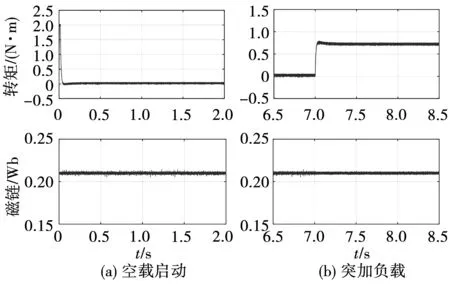
图10 模糊控制代价函数的控制性能Fig.10 Control performance of MPTC whose cost function with fuzzy control

4 实验验证

使用dspace平台对本文提出的方法进行验证，电机参数除转动惯量和阻尼系数外，其他和表1中的内置式永磁同步电机相同，仿真步长设为50 μs，直流稳压电源设为30 V。负载采用的是发电机电阻负载：电动机通过转轴拖动一台表贴式永磁同步发电机，发电机发出的电经过二极管整流桥整流成直流电压，直流电流流经电阻负载。

电机的给定速度为120 r/min，磁链给定值为0.21 Wb。空载起动后通过开关连接发电机电阻负载。实验时发现，在预测转矩控制中采用不同代价函数，电机的起动转速响应快速性相差不大，电机带负载稳态时的结果分别如图11、图12、图13所示。

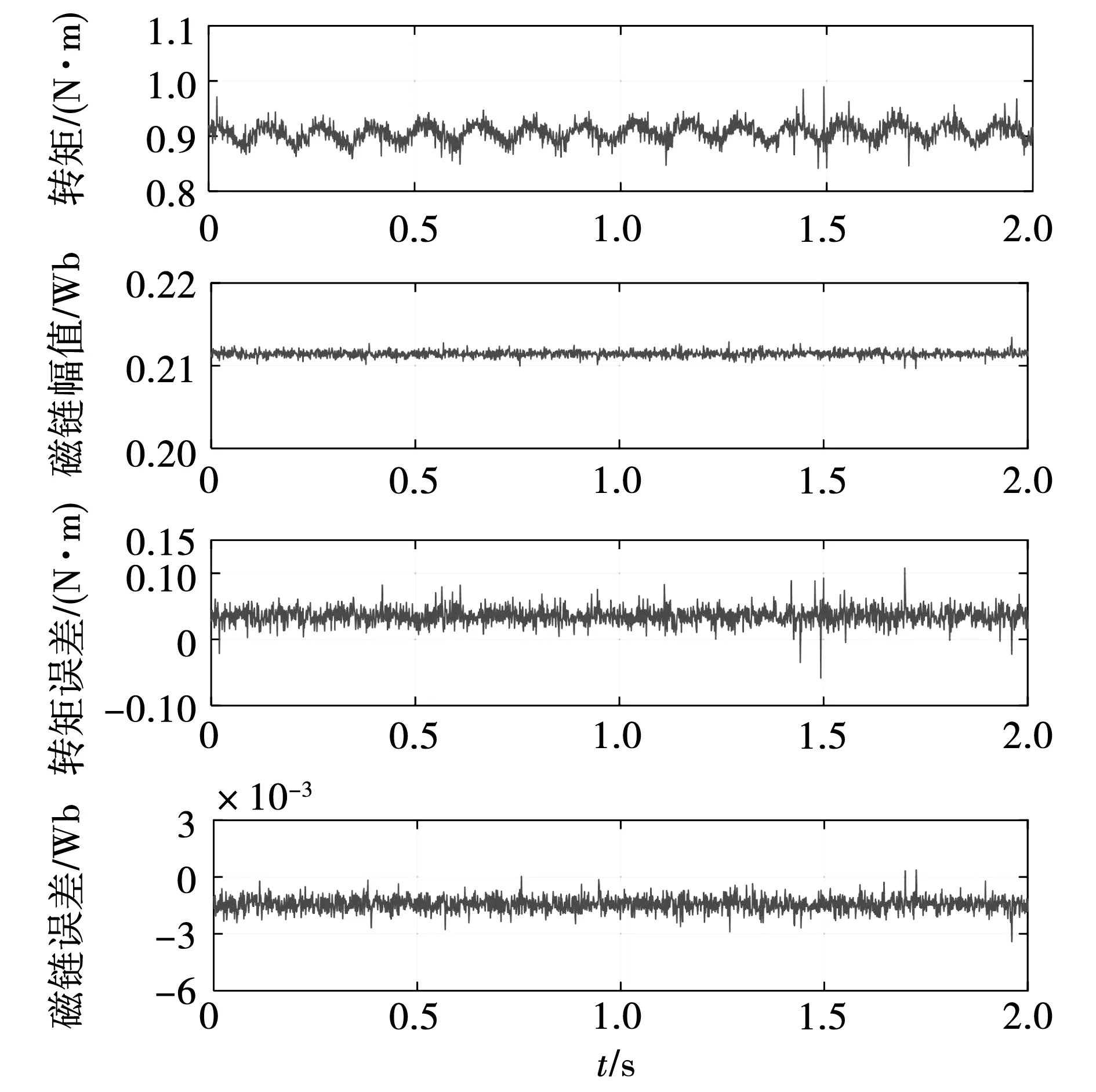
图11 常规代价函数MPTC的稳态性能Fig.11 Steady-state performance of MPTC whose cost function is conventional

图12 无权重系数代价函数的稳态性能Fig.12 Steady-state performance of MPTC whose cost function has no weight coefficient

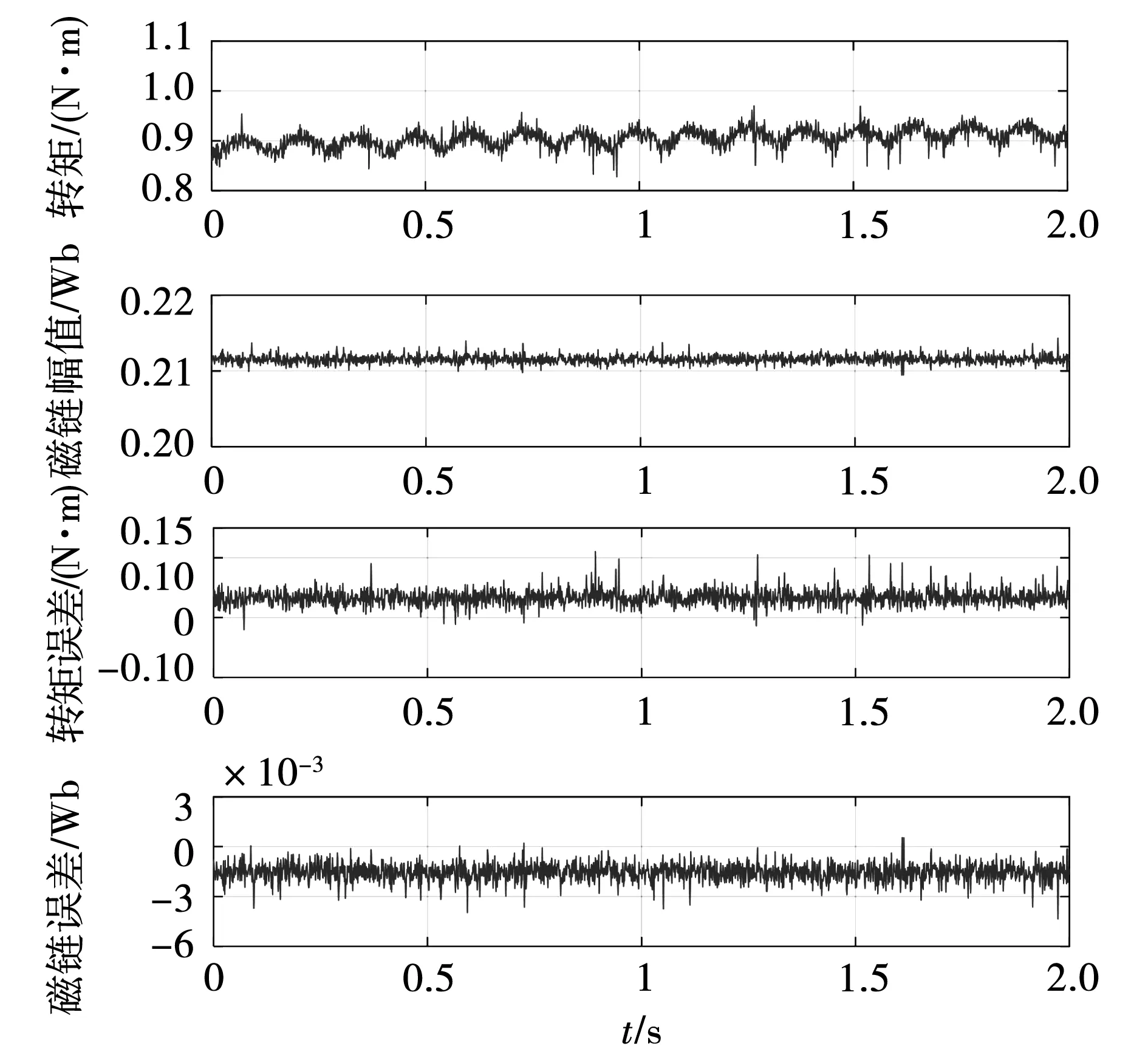
图13 模糊控制代价函数的稳态性能Fig.13 Steady-state performance of MPTC whose cost function with fuzzy control

下式为计算转矩和磁链的RMS控制误差，其中n为采样数据个数:

(10)

计算结果如表3所示，在这三种MPTC模型中，采用模糊控制代价函数的转矩RMS控制误差最小，同时它的磁链RMS控制误差处于这三种居中。综合来看，模糊控制代价函数的MPTC模型的稳态性能更好。

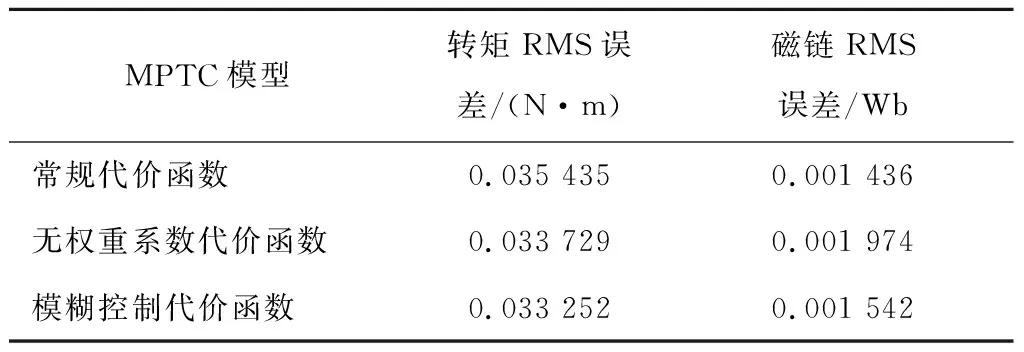
表3 稳态转矩磁链比较

5 结 论

本文对直接转矩模型预测中采用恒定数值权重系数的代价函数进行了分析，提出了采用模糊控制调节权重系数的直接转矩模型预测方法，权衡了转矩和磁链这两个控制目标。根据定子d-q轴电流的变化调节权重系数，可以直观地反映出代价函数中磁链和转矩的控制效果。与常规代价函数和无权重系数的代价函数相比，从转矩和磁链这两个控制目标综合来看，该方法的转矩和磁链RMS控制误差更小，具备更佳的性能表现。