基于动态式双阈值的锂电池组主被动均衡策略

王鹿军， 单恩泽

(湖北工业大学 太阳能高效利用及储能运行控制湖北省重点实验室，湖北 武汉 430068)

0 引 言

在对汽车供能方面的研发中，锂离子电池作为无污染性储能单元而被重视。其在电能容纳量、能量使用效率以及使用年限等方面颇现优异[1]。由于不同功率负载对于电压的要求存有差异性，故锂离子电池多以成组方式使用，进而暴露出不同工况下各单体电池不一致性的问题[2]。电池均衡技术可改善此类问题，具体体现在电池能量的使用程度以及电池循环寿命等方面[3]。

在均衡策略中，常采用电压或者荷电状态(state of charge,SOC)判断电池是否需要均衡[4]，此外电池容量及开路电压等亦可[5]。文献[6-7]采用电池容量或者剩余容量作为均衡判据，但每个单体电池充入或放出相同的电量时易出现单体电池电压或者荷电状态的极端变化现象。文献[8-10]依据开路电压建立均衡控制策略，但各类型电池的充放电特性曲线不一致并且易受工况环境的影响，而且在测量电池开路电压的静置期间，极易产生因误差波动不稳定而导致的精确度失准问题。文献[11-13]用电池端电压作为均衡判据，在工作状态下受工作条件等因素影响较大，并且电池组在循环充放电中的平台期时，容易出现低容高压的单体电池能量传递到高容低压电池的现象，进而扩大了电池容量的不一致性。文献[14-16]以SOC作为判据，但其不能直接测量，环境变化会使测量结果出现偏差，导致SOC值漂移，多种类的叠加误差会随着时间的推移而累积，所以估算算法的精确度要求高，且无法减小或消除电池实际容量的差异。文献[17-19]中通过耦合多个不同目标作为均衡判据，但多目标均衡中各目标之间控制关系复杂，均衡控制系统结构复杂，其中的耦合条件也只适用于理想工作环境中，各目标不均衡程度的加权系数确定困难,其应用受到一定程度的限制。

基于对上述不同类型均衡控制策略的分析，本文提出一种基于动态式双阈值的锂电池组主被动均衡控制策略。首先，该策略通过对锂离子电池的充放电过程实时细化，选择电压和SOC作为双阈值均衡判据。其次，利用温度变化作为干扰因素，模拟锂离子电池组的不同工况，得出动态式双阈值判据，提高其充放电的精确度。最后，将此均衡策略运用到主被动均衡电路中，通过仿真实验证实所提出控制策略的可行性。

1 均衡电路及其原理分析

1.1 主被动均衡电路

针对三元锂离子电池组的整个充放电过程，在不降低均衡效率的前提下，最大化提高均衡电路充放电精确度，减少能量循环次数。提出了如图1所示的主被动均衡电路。

图1 电池均衡电路图Fig.1 Battery equalization circuit diagram

由图1可知，整个均衡拓扑结构由被动均衡、电池组和主动均衡三个部分组成。电池组由N个三元锂离子单体电池串联而成。主动均衡电路依据LC振荡电路原理。该主被动均衡电路的特点：

1)被动均衡控制简单且均衡电流较小，能够在充放电初期和末期延缓电池容量增加速率，更为精准地测量估算出当前电池组充电状态。

2)开关矩阵含有N+1个双向MOSFET开关管，在保证电路高转换效率的前提下，缩减元器件使用数目，实现电池组中多对一的能量转移方式。

3)主动均衡部分采用LC振荡电路，结合含4个双向MOSFET开关管的均衡方向选择电路，灵活控制流经电容的电流方向，增大均衡电压差。

4)在电池组充放电过程中，较大的主动均衡电流，可以快速实现能量内部转移，一定程度上弥补混合电路中被动均衡带来的均衡速率问题。

1.2 工作原理分析

被动均衡电路的结构和工作原理简单易控制。当符合均衡判据条件时，充放电阶段导通功率开关管，通过旁路有效负载控制充放电速率[20]。其中，消耗负载上的分流电流须远大于锂离子电池的自放电电流。主动均衡电路控制较为复杂。如图2所示，以四节锂离子电池串联为例，介绍其工作原理。

图2 主动均衡电路图Fig.2 Active equalization circuit diagram

假设锂电池组中的单体电池B1电量高，且达到均衡条件，与之均衡的是单体电池B2，选择电感L和电容C2组成的支路。如图3所示，是一个完整的能量传递过程。

图3 主动均衡工作过程Fig.3 Active equalization process

主动均衡的一个周期可分成四个阶段，首先B1放电并将电能储存在电容C2中，接着电容C2给电池B2充电，实现能量转移。随后控制方向选择电路，保证电池B1充电方向与电容的放电方向一致，完成一次换向并且提高下一周期均衡电压和电流。最后，电容的电压电流切回初期阶段的方向，保持下一个周期电路的正常运行。通过仿真实验，电感L与一个电流表连接，从Scope of IL1中显示电流波形，电容C2与一个电压表并联，从Scope of UC中显示电压波形如图4所示。

图4 电流电压变化波形图Fig.4 Current and voltage variation waveform

由图4可知，均衡电路控制的一个周期中，电流在每个过零点时，电容的储能方向将会改变一次。当电流达到每个阶段中的最小值时，电流改变方向，进一步将能量储存在电容中，达到增加压差的目的，为下一次储能方向的改变做准备。T1和T4所处阶段的作用是正向吸收前一次电容放电后的残余能量，T2和T3所处阶段是反向吸收能量，此处时间的长短可以根据实际情况做调整。

2 均衡控制策略

传统的双阈值方法多是单独从电压或者荷电状态内进行另一阈值选择，从而形成双阈值[21]，本文针对三元锂离子电池，采用以端电压和荷电状态作为双阈值输入量并耦合参与整个均衡过程，合理调整阈值控制方法，相较于传统的双阈值方法，该方法更适用于整个充放电过程在提高精确度的同时，也避免了均衡电路控制中开关器件的频繁接入，从而降低器件损耗，提高均衡速率。

2.1 锂离子电池等效电路模型

模型电压源受控于实验所设置的荷电状态，并确保电池的特性曲线适用于受控电压源，使得所建立的二阶RC等效电池模型在描述电池荷电状态全程中具有较高的精确度，并且可得出契合度较高的电压值。该模型结构如图5所示。

图5 二阶RC等效电池模型Fig.5 Second order RC equivalent cell model

图5中：UOCV为开路电压；R0为等效欧姆内阻；R1和R2为极化产生的等效内阻；U为端电压。参数辨识通过脉冲放电试验来实现，等效模型中各参数辨识结果见表1。

表1 模型参数辨识表

根据基尔霍夫电压定律，可得以下数学关系式：

U=UOCV+iR0+U1+U2；

(1)

U1=iR1(1-e-t/R1C1)+U1(0)e-t/R1C1；

(2)

U2=iR2(1-e-t/R2C2)+U2(0)e-t/R2C2。

(3)

2.2 动态式双阈值相关参数分析

模型包括的主要输入量有：端电压、SOC、温度。输出量为：电压差阈值和SOC差阈值。

由于模型在建立当中，存在着不同度量尺度的三个关键输入信息，故将对其中的端电压和SOC做归一化处理，即

(4)

式中：Var表示端电压或者SOC归一化后的数值；Ti是原始测量计算数据，最终Var数值的取值范围是0到1。

三元锂电池特性曲线中存在多段类似线性关系区间，常规数学处理思想是化曲为直[22]，但该方法在所选分段区间较大的实验中误差高达36.7%，故采用添加辅助函数关系式进行调整，在t时刻对单体端电压进行线性表征为：

(5)

式中：Hn(t)表示单体电池的端电压函数；Ψn(t)是辅助函数；λn是第n节单体电池在t时刻的电压振动系数，该系数主要作用是匹配归一化的数据和适度调整电压测量误差；Un(t)为t时刻第n节单体电池的端电压。

模型预测中，多处等间距时间和SOC数据测算时存在自变量与因变量成线性关系的情况，使用逐差法对存在线性相关的区间进行数据归类，即

(6)

式中：η(t)代表在t时刻整组电池间的荷电状态偏差值；SOCn(t)表示在t时刻的第n节电池的荷电状态情况。

图5中给出的二阶RC电池等效模型中存在两个RC环节，直接影响到模型端电压的精确度，故在Ψn(t)辅助函数中加入带有C1和C2的函数关系环节，具体计算过程如下：

(7)

式中：U(t)表示在t时刻测得的电池端电压；Ugiv表示Ψn(t)辅助函数中的端电压修正部分；Is表示流经电池的总电流。各参数的取值方法如下：

(8)

τn=Rn·Cn。

(9)

对于电池荷电状态部分，选择温度影响作为模型验证中的不稳定变量。根据二阶RC锂电池模型和初期数据处理中使用过的安时积分法，得出电池系统状态方程，该方程是以模型中的SOC、U1和U2为状态量，离散化处理可得：

(10)

τn,j-1=Rn,j-1·Cn,j-1。

(11)

式中：j是序列控制数；T是控制周期；ρj是在第j个时间内的充放电效率。由KMF原理代入方程，得出荷电状态估算式。

2.3 温度对动态式双阈值参数的影响

本次实验选择16节单体三元电池，在恒温箱中进行实验测试。所使用的单体电池容量为4 200 mAH的18650型LiCoMnNIO2单体电池，全程记录实验数据，并对所有电池做数据处理分析，以10组单体电池的平均数据值作为绘图数据支撑，最终得出不同温度OCV-SOC的曲线如图6所示。

图6 不同温度下的OCV-SOC曲线Fig.6 OCV-SOC curves at different temperatures

针对图6温度变化对于阈值估算精确度的影响分析，选择在不发生过充过放情况下的温度变化范围，即零下15 ℃到45 ℃，选择5个特定温度下的特性曲线进行比较分析。

图7所示为在不同温度下，单体锂电池的开路电压相对于稳定工作状态的偏差，并且以荷电状态作为分段度量标准，旨在体现锂电池在充放电过程中，温度对于电量表征的影响也明显存在，此处可能会导致所测量的数据失准。

图7 各温度下的辅助调整函数曲线图Fig.7 Curve of auxiliary adjustment function at each temperature

表2中数据表示在不同温度下，三元锂电池的温度修正电势函数，从式(5)可见，与开路电压和端电压计算相关的函数，除了自身的相关系数以外大多与时间保持关系，此处的温度修正电势函数是单纯与荷电状态相关联，即

表2 温度修正电势差函数相关数据

(12)

式中：ΔE(soc)为温度修正电势差；S和Bn是定量数值。将温度影响带入到电池等效模型中，三元锂电池的输出电压表达式为：

UB=UOC-IB×Zeq+S(t)=

UOC(soc,t)-U1(t，τ1)-

U2(t，τ2)-UR(t)+ΔE(soc)。

(13)

式中：各参数随时间变化，UB表示输出电压；UOC表示开路电压；IB为负载电流；Zeq为等效内阻；t为采样时刻；UR(t)表示等效欧姆内阻的电压；S(t)是模拟环境因素的观测噪声。

2.4 动态式双阈值判据取值方法

本文以三元锂离子电池为例，说明合理选择阈值的方法。动态式双阈值判据取值方法选择在温度扰动的前提下进行描述。

图8中的GRA(SOC)表示单位SOC内OCV变化率的曲线图，针对ΔSOC阈值大小的选择。GRA(OCV)表示单位OCV内SOC变化率的曲线图，针对ΔU阈值大小的选择。两条曲线目的在于找到OCV最小变化率和SOC最大变化率。

图8 开路电压和荷电状态斜率图Fig.8 Open circuit voltage and state of charge slope diagram

下周期阈值的确定，按照上周期输出阈值大小设定差值并订正阈值数。实时监测电池电流和端电压，防止判据失准问题，对此时的电流进行SOC估算，对端电压差值进行开路电压换算，两项结果作为校验双阈值取值正确合理性的依据。

选择三种确定阈值的方法：经验固定阈值、以电压或者SOC作为单阈值的动态调节阈值、电压和SOC耦合动态调节阈值，如图10所示。三种方法均以5 mV的电压阈值作差，会在±10 mV的电压差内波动变化。图中曲线还考虑了电压阈值误差，以解决电压提前达到设定的均衡电压差阈值或反向超过此阈值的问题。

图9 双阈值选择流程Fig.9 Dual threshold selection process

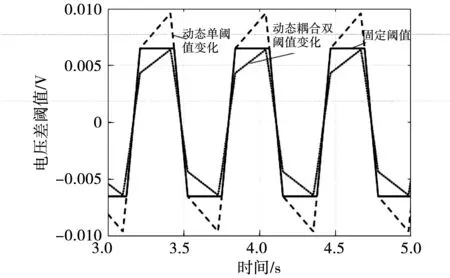
图10 三种电压阈值选择方法比对图Fig.10 Comparison of three voltage threshold selection methods

图11(a)表示定值电压阈值和动态式双阈值中电压部分差值波动变化，在均衡电路开启的前期，动态阈值变化十分明显，但最终稳定在10 mV的范围内波动。

图11(b)是与文献[14]中的方法做对比得出的荷电状态波动图，反映出锂离子电池SOC的阈值判据是会随着时间变化的。荷电状态变化最终趋于稳定状态，也可以达到传统方法中采用固定阈值的阶段，两者并不矛盾。

图11 八节单体电池阈值误差图Fig.11 Error chart of threshold state of charge of each cell

2.5 均衡控制策略

均衡电路根据当前电池组所处工作状态，被选择性地及时并入电池组进行均衡。主动均衡参与放电过程和中间部分充电过程，被动均衡参与充电前期和末期两小段，如图12所示。

图12 主被动均衡作用区域图Fig.12 Active and passive equilibrium action area diagram

放电阶段启动主动均衡，减少能量损耗，更多输出电能到负载；充电阶段被动均衡免除大电流充电对电池造成的损耗，预热充电，收尾时避免电池过冲；中间段使用主动均衡，大电流充电，电池SOC快速达到预定阈值。

图13 混合控制流程Fig.13 Mixed control process

当SOC小于15%时,系统接入被动均衡电路并以小电流对电池进行恒流充电。当SOC大于15%且小于85%时，切换到主动均衡电路并以大电流对电池组进行恒流充电，达到快速充电效果。当SOC大于85%时，系统再次切换被动均衡电路并且选择恒压充电模式，最终达到100%结束。

3 均衡实验与分析

MATLAB/Simulink搭建电路仿真模型，模型包括1个控制模块、1个过渡模块、3个执行模块、8个电池模型和1个恒流源。仿真实验具体参数见表3。

表3 仿真实验参数

3.1 电池组静置状态实验与分析

内部电池组间进行均衡能验证动态式双阈值控制有效性。各电池电压值出现较大差异时均衡效果更明显。如图14所示，电池组中最大电压差为94 mV，电池1的电压增加快，电池7和电池8的电压降速较缓，在5 940 s左右达到均衡。

图14 静置状态下的电池均衡Fig.14 Battery equalization in static state

由此可见，提出的控制策略可以达到预期的均衡效果，均衡结束后的各单体电池间的电压波动在5 mV内，具体均衡情况见图15。

图15 静置状态均衡实验相关数据Fig.15 Related data of static state equilibrium experiment

3.2 电池组充电状态实验与分析

由电流值为5 A的电流源供电，开关频率为50 kHz，占空比为65%。各单体电池的初始电压为：3.768、3.806、3.822、3.833、3.840、3.866、3.887、3.893 V。电池间的最大电压差值为125 mV，动态式双阈值判据均衡均衡情况如图16(a)所示，单阈值电压判据均衡如图16(b)所示。

图16 不同判据下的充电状态均衡对比图Fig.16 Comparison chart of state of charge equalization under different criteria

仿真实验结果表明，电池组在3 880 s附近达到理想均衡效果，最终保持在4.19 V左右，八节电池电压差不超过7 mV。其中，在整个电池组SOC达到90%以上时充电电压上升曲线明显缓和。此外，以单阈值电压为判据的均衡方法，在均衡结束后电池间电压波动较大，最大电压差达到14 mV，均衡时间较长，动态式双阈值判据均衡时间缩短近15%。

3.3 电池组放电状态实验与分析

静置状态和充电状态下都以电压值表示结果，为了验证电池荷电状态的准确性，选择以电池SOC作为采集数据。采用5A的电流源恒流放电，开关频率为50 kHz，占空比为55%，如图17所示。

图17 不同判据下的放电状态均衡对比图Fig.17 Comparison diagram of discharge state equilibrium under different criteria

放电实验是以SOC单阈值为判据均衡，最终SOC值波动较大，最大SOC差值达到1.85%，在4 000 s后达到均衡要求。反观动态式双阈值方法的均衡电池组除组内波动小外，均衡时间也缩短了19%左右。八节锂离子单体电池以SOC单阈值判据均衡方法，在放电状态下如图17(b)所示。

3.4 实物实验

搭建的实验平台如图18所示，供电部分由两节电池通过升压模块提供，负载由滑动变阻器模拟，滑动变阻器的最大电阻为100 Ω。

图18 实验平台Fig.18 Experimental platform

需验证的工况是系统循环工作时的电流值变化，使用EVT充放电设备对两组6节单体电池进行模拟实验，分别如图19和图20所示。

图19 2C充电下的SOC变化图Fig.19 Diagram of SOC change under 2C charging

图19中设置充电电流为2C倍率，充电5 min后，测得第一组6节电池产生不一致性，此时6节电池SOC分别为28%、29.8%、30.2%、32%、32.3%、33%。根据本文的均衡系统规则，最先将6号电池和1号电池进行均衡。充电开始后，发现5号电池的SOC上升速度也明显增快，原因在于均衡充电启动程序中，若最大SOC电池与相邻电池间的差值超过阈值0.5%，则3个电池一起均衡。故在约50 s之前1号和5号电池的SOC上升斜率较大，6号电池的最小。在200 s时，均衡进入结束阶段，此时各单体电池的SOC分别为35.4%、35.3%、35.4%、35.5%、35.5%、35.5%。

图20为测试均衡系统的小电流放电工况，接入本文均衡系统的第二组6节电池组进行循环充放电实验，0.5C放电60 min后，2C充电10 min为一个循环，记录12个小时循环充放电的6节电池SOC值。实验开始时，测得第二组6节电池SOC分别为79.8%、80.1%、80.3%，80.5%，81%、81.3%。

图20 0.5C放电下的SOC变化图Fig.20 Diagram of SOC change under 0.5C discharging

放电开始前，1号电池的SOC显示最大，6号电池的SOC显示最小，根据本文均衡系统的放电规则，最先将6号电池和1号电池均衡。由于在1号电池和2号电池间的SOC差值没有达到阈值范围内，故两者间没有均衡现象。以0.5C放电时，整体的SOC下降斜率较小，在320 s的时候，各单体电池的SOC值为77.5%、77.4%、77.6%、77.8%、77.7%、77.8%。

4 结 论

通过研究主被动混合均衡电路的理论可行性，将主动均衡大电流特点与被动均衡简单控制特点相结合，提出与该电路相匹配的基于动态式双阈值的均衡控制方法。

1)选择出现电池间反复充放电次数较多的LC振荡电路作为主动均衡电路，对充放电状态下的电池组采用单阈值和动态式双阈值两种方法做对比试验。

2)动态式双阈值均衡策略是以电压、SOC和温度为变量，将均衡开启所需阈值的大小进行动态处理，其次控制流程中的区间划分亦可动态调整。与单阈值型均衡对比，该策略缩短了15%到19%的均衡时间。

3)区间变流充放电的混合均衡方式减缓了末期电压的增速，延长反应时间，降低了过充过放现象发生的可能性；

4)整个均衡过程的速度并未因被动均衡的加入而减小。