基于数据驱动的永磁同步电机深度神经网络控制

李耀华， 赵承辉， 周逸凡， 秦玉贵

(长安大学 汽车学院，陕西 西安 710064)

0 引 言

有限状态集模型预测控制(finite control set model predictive control，FCS-MPC)基于电机的系统预测模型，充分利用逆变器的离散特性和开关状态有限的特点，遍历计算所有开关状态作用下的系统动态行为，并基于成本函数最小化的原则选择最优电压矢量用于逆变器开关状态的响应，近年来在电机控制领域受到了广泛关注[1-5]。

FCS-MPC通过遍历计算所有的备选电压矢量，导致算法计算量较大难以在实际应用中实施。文献[6]舍弃了部分预测价值较小的电压矢量，只对特定候选状态进行预测运算。文献[7]从减少开关次数出发，舍弃开关次数较多的电压矢量。文献[8]通过定子磁链扇区和转矩增减信号，舍弃不满足转矩控制的电压矢量。文献[9]在扩展电压矢量的基础上，通过定子磁链扇区、转矩和磁链增减信号对备选电压矢量进行精简。文献[10]通过统计不同定子磁链扇区、转矩和磁链增减信号及转矩角下，模型预测控制电压矢量利用率的情况，舍弃利用率较低的电压矢量。文献[11]对比分析采用不同备选电压矢量集合的控制性能。以上方法均从减少备选电压矢量个数出发，减轻系统运算量，提高系统实时性，但其将模型预测控制原有的全局最优变为局部最优，牺牲了一定的系统控制性能。因此，在保证模型预测控制遍历所有可能状态获得全局最优的前提下，提高控制实时性是本文的研究重点。

神经网络通过对数据的学习和训练能够充分逼近复杂的非线性映射关系，将所有定量或定性的信息分布储存于网络的各个神经元中实现并行分布式的储存和运算，具有快速大量运算的能力和线上推理速度，可满足实时性要求[12-13]。目前研究大多将神经网络应用于转矩观测[14]、电机参数辨识[15]和最大转矩电流比控制实现[16]等。

本文将模型预测转矩控制(model predictive torque control，MPTC)选择最优电压矢量的过程视为非线性映射下的多分类任务，通过采集其运行数据离线训练一个深度神经网络(deep neural network，DNN)，使神经网络充分逼近MPTC的选择规律，从而取代其进行最优电压矢量的选择，通过扩充动态数据，解决因动静态数据失衡引起的系统失控问题，并通过更换训练数据，验证DNN具备学习非线性约束下的控制规律的能力。仿真验证基于数据驱动的永磁同步电机神经网络控制的可行性。

1 永磁同步电机模型预测转矩控制

1.1 表面式永磁同步电机模型

定子磁链坐标系下表面式永磁同步电机转矩方程如式(1)所示，Te(k)、ψs(k)、δ(k)、p、ψf和Ld分别表示当前k时刻下的电机转矩、定子磁链幅值、转矩角以及电机极对数、永磁体磁链和d轴电感等参数。忽略定子电阻压降的影响，施加电压矢量Vs(k)并作用Δt时间后的定子磁链ψs(k+1)如图1和式(2)所示，其中：α为施加的电压矢量与定子磁链ψs(k)的角位置θψs的夹角；q为中间变量；Δθs表示电压矢量作用下的定子磁链角度的变化量。

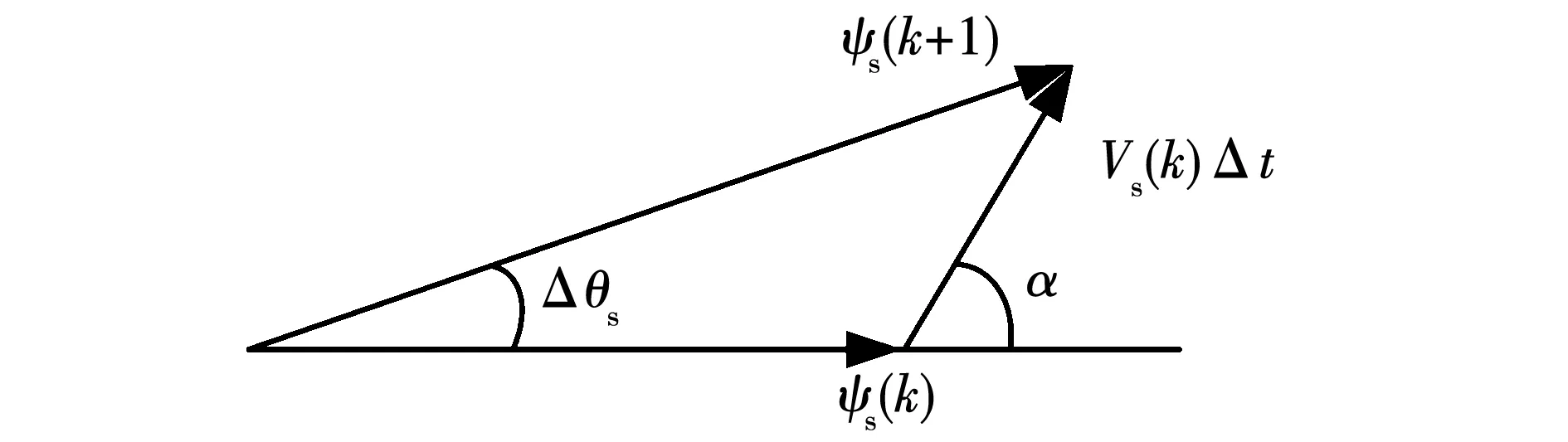
图1 定子磁链运动变化过程Fig.1 Move of stator flux

(1)

ψs(k+1)=ψs(k)+Vs(k)Δt,

(2)

忽略转子运动，根据余弦定理和正弦定理可以计算Vs(k)作用后第k+1周期的定子磁链幅值和转矩角[17-20]分别为：

(3)

δ(k+1)=δ(k)+Δδ=δ(k)+

(4)

将式(3)和式(4)代入式(1)可得表面式永磁同步电机第k+1时刻的电机转矩预测方程为

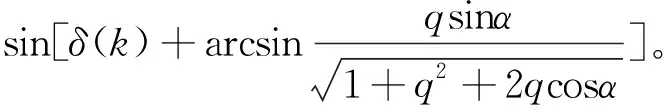
(5)

1.2 备选电压矢量集合与成本函数

模型预测转矩控制备选电压矢量采用逆变器产生的全部7个基本电压矢量，即

Vs∈{V0,V1,V2,V3,V4,V5,V6}。

(6)

式中：Vs为备选电压矢量；V0～V7为逆变器产生的7个基本电压矢量。零电压矢量可由两个开关状态(111或000)生成，具体选择以开关次数最小为原则[21]。

定义表面式永磁同步电机模型预测转矩控制的成本函数为

g=

(7)

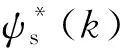
表面式永磁同步电机模型预测转矩控制系统如图2所示。

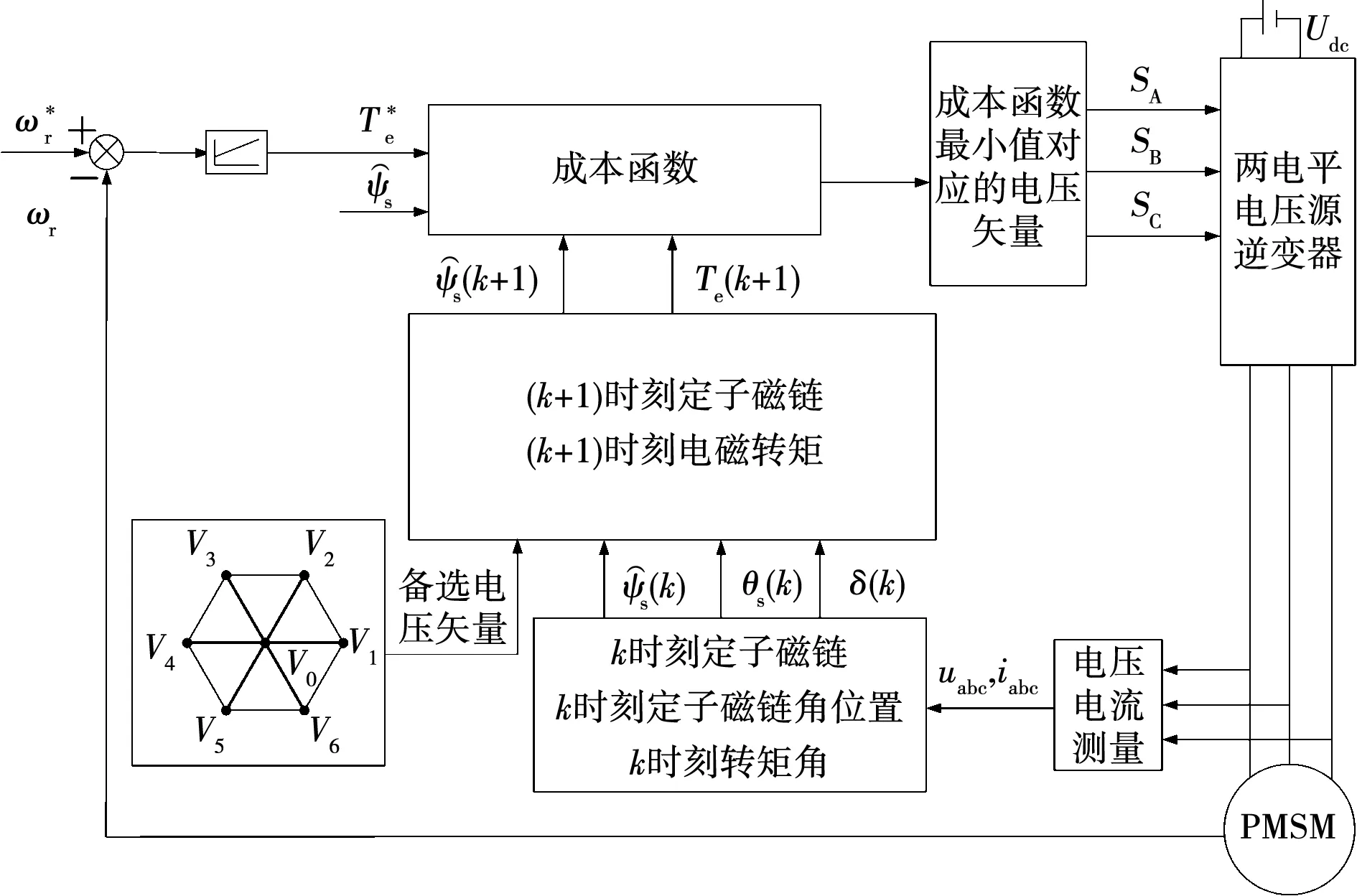
图2 表面式永磁同步电机模型预测转矩控制系统Fig.2 SPMSM MPTC system

2 基于数据驱动的神经网络

如上文分析，模型预测转矩控制根据成本函数从7个备选电压矢量中选择最优电压矢量，可将该过程视为一个非线性映射下的多分类任务。因此，可以基于数据驱动来训练神经网络学习并逼近该分类过程的控制规律，从而代替模型预测转矩控制。

基于数据驱动的神经网络控制流程如图3所示，其主要由特征工程建立、训练数据采集与预处理、网络构建、训练、评价与应用等组成。

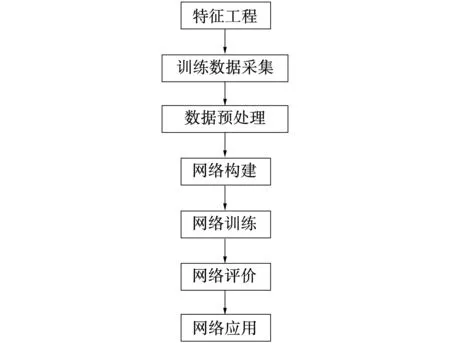
图3 基于数据驱动的神经网络控制流程图Fig.3 Control chart of neutral network control

2.1 特征工程建立

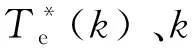
2.2 训练数据采集与预处理

基于MATLAB/Simulink建立表面式永磁同步电机模型预测转矩控制仿真系统模型，用于训练数据的营造和收集。仿真模型为离散模型，采样周期为5×10-5s。直流母线电压为312 V，转速PI调节器参数为Kp=5，KI=100，PI调节器输出上下限为[-35 N·m，35 N·m]。参考定子磁链幅值为0.3 Wb。仿真用表面式永磁同步电机参数如表1所示。

表1 仿真用表面式永磁同步电机参数

训练数据建立的仿真条件如下：设置参考转速分别为-500、-300、-100、100、300、500 r/min，使用斜坡函数设置负载转矩在1 s内从-30 N·m变化到-10 N·m及1 s时间内从10 N·m变化到30 N·m。设置负载转矩分别为-34、-30、-25、-20、-15、-10、10、15、20、25、30、34 N·m，使用斜坡函数设置参考转速在2 s内从-500 r/min变化到500 r/min和在2 s内从500 r/min变化到-500 r/min。通过以上36组仿真试验，收集特征工程确定的神经网络4个输入量和1个输出量运行数据，共得到1 200 000组训练数据。对训练数据进行标准化，使其满足均值为0和方差为1的正态分布，并按照9∶1比例划分训练集和测试集两部分数据，前者用于网络训练，后者用于网络测试评价。由于数据量较大，本文使用批数据训练，批数据尺寸设置为2 000。

2.3 网络构建、训练、评价和应用

神经网络的层数越深，学习能力越强，但结构也越复杂。通过试验，确定采用1个输入层，5个隐含层和1个输出层的DNN网络，其拓扑结构和训练过程如图4所示。

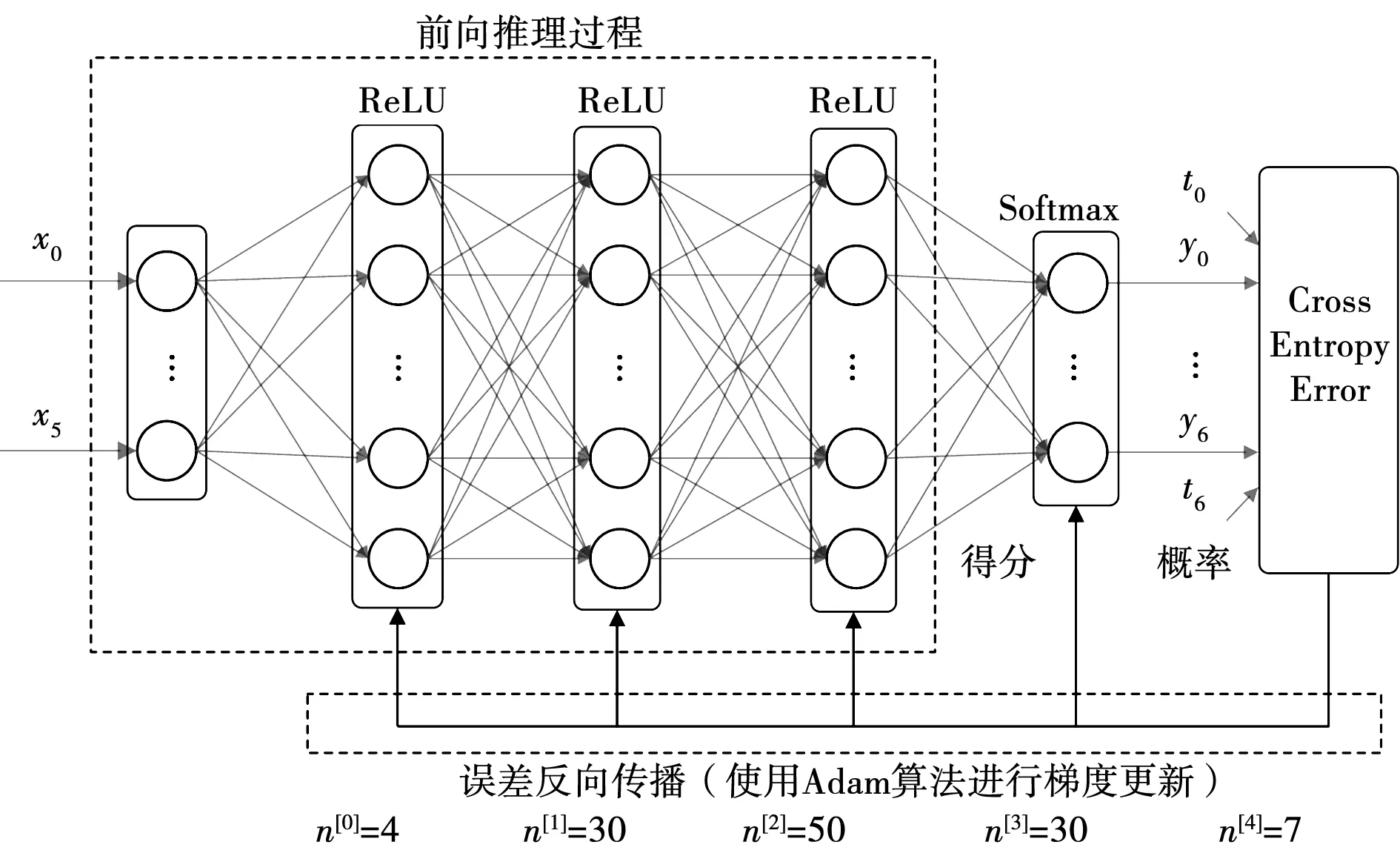
图4 DNN网络拓扑与训练过程Fig.4 Topology and training of DNN

DNN网络各神经层的神经元节点数目{n[0],n[1],n[2],n[3],n[4]}分别为4, 30, 50, 30, 7。隐含层间的传递和变换关系如下，第h层的输出xh通过上一层的输出xh-1与当前层的权值矩阵wh和偏置矩阵bh的运算，经过激活函数非线性化得到：

xh=ReLU(xh-1*wh+bh),

(8)

使用线性修正单元函数ReLU(rectified linear unit)作为各隐含层的激活函数，即

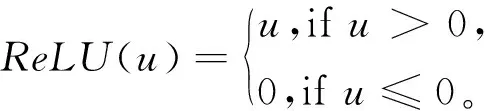
(9)

网络训练包括前向推理和误差反向传播两个过程。前向推理过程主要执行如式(8)所示的多次层间变换，最终输出对应7个基本电压矢量的7个类别得分，并通过如式(10)所示的softmax函数将得分转换为概率分布，式(10)中a(k)为类别得分，n为输出层的神经元总个数。误差反向传播过程主要通过梯度法寻找使损失函数E减少最多的方向，并逐步更新wh和bh参数。使用交叉熵误差作为损失函数，采用Adam梯度算法进行梯度更新。

(10)

重复前向推理和误差反向传播两个过程，梯度将逐渐下降，网络参数逐次迭代更新，损失函数值随之减小，DNN网络也逐步逼近MPTC选择规律。重复次数设置过多或多少，对DNN网络的效果都不利，前者会引起过拟合，使得网络仅对训练数据具有良好的分类性能，对新样本的分类性能较差，泛化性能较差；后者会引起欠拟合，使得网络对训练数据训练不充分，未能建立起关于训练数据非线性映射的精确模型，网络不具备可用性。通过试验，确定重复次数为30次，其中学习率设置为0.01。

将DNN与MPTC选择的电压矢量相同的百分占比情况定义为准确率，用于评价DNN分类性能的优劣。DNN训练集和测试集的一致率如图5所示。

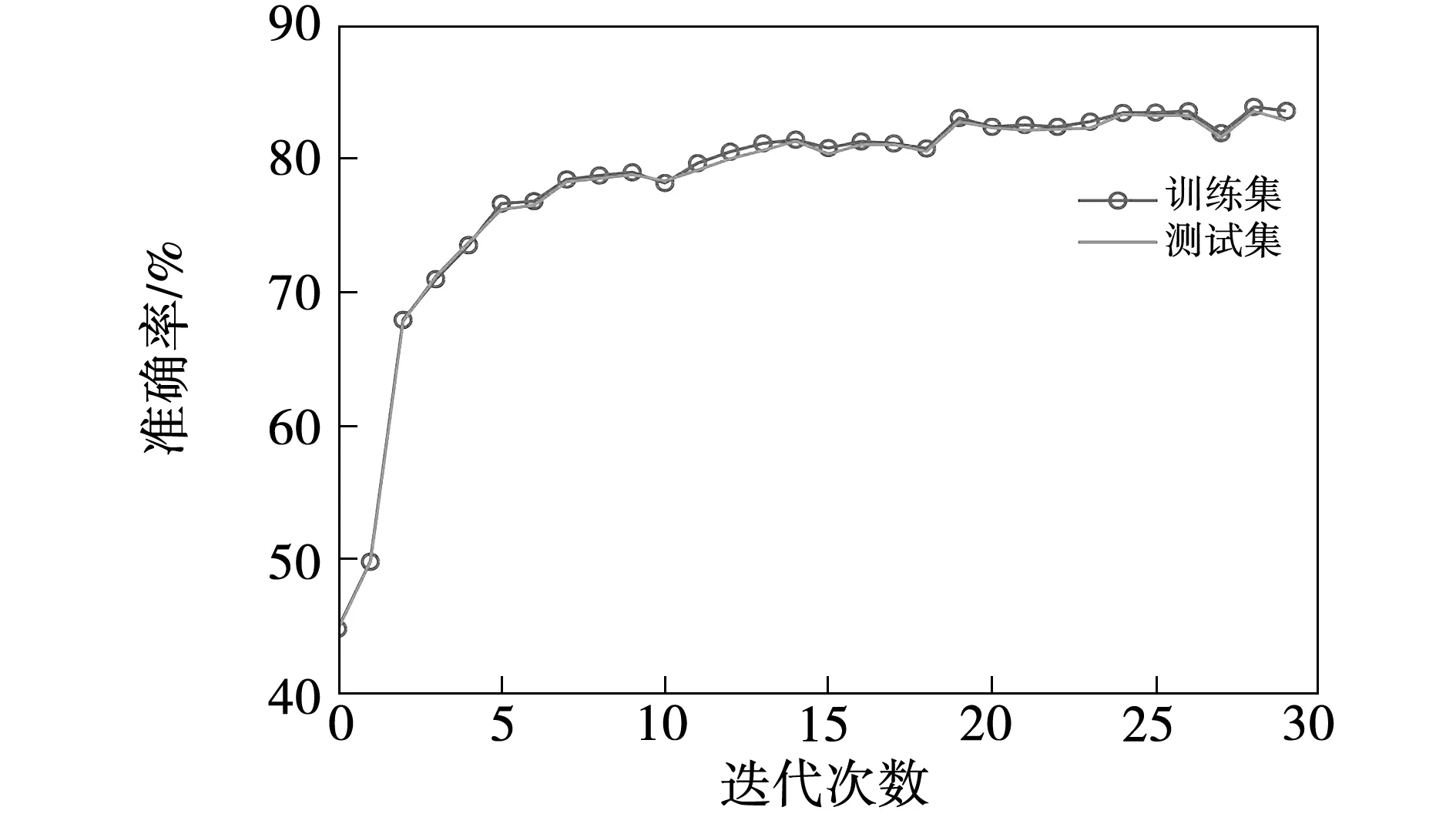
图5 训练集和测试集的准确率Fig.5 Accuracy of train set and test set

图5表明随着训练过程的进行，准确率逐步上升并趋于稳定，训练集和测试集的准确率曲线基本吻合，表明没有出现过拟合和欠拟合，网络在未知新样本上的分类性能和可用性得到了保障。经过30次重复训练， DNN网络在训练集和测试集上的准确率均达到约84%，说明网络分类效果较好，逼近了模型预测转矩控制的控制规律。

将训练成熟的DNN取代原有的模型预测控制策略，嵌入至永磁同步电机系统控制系统，从而实现基于数据驱动的永磁同步电机深度神经网络控制系统，如图6所示，其中虚线部分为数据集建立和DNN离线训练过程。DNN网络输入为特征工程的4个输入，输出为施加的电压矢量。当网络训练成熟时，网络的权重和偏置等参数已经整定完毕，在网络使用过程中DNN仅需执行前向推理过程即可根据最大得分得到分类结果，无需softmax转换和损失函数计算，从而可提升系统实时性。通过MATLAB/Simulink和Python/Pytorch联合仿真实现控制策略验证，其中通过编写S函数调用Python脚本的方式完成DNN分类器的嵌入。

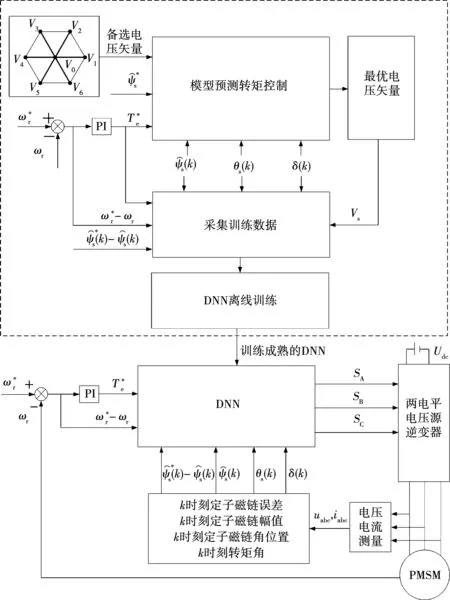
图6 永磁同步电机深度神经网络控制系统Fig.6 PMSM DNN system

3 仿真验证

下文对基于MPTC和基于DNN的永磁同步电机系统进行仿真验证对比。

电机系统参数与上文一致，参考转速初始值为60 r/min，1 s时阶跃至-60 r/min，负载转矩初始为15 N·m，0.5 s时阶跃至-15 N·m，1.5 s阶跃至15 N·m，仿真总时长为2 s，从而建立含电机四象限运行的复合工况。

为了定量评价控制效果，定义转矩脉动均方根误差(root mean squared error,RMSE)和磁链脉动均方根误差如下：

(11)

(12)

其中n为采样个数。

基于MPTC控制下的永磁同步电机转速、转矩和定子磁链幅值如图7～图9所示。

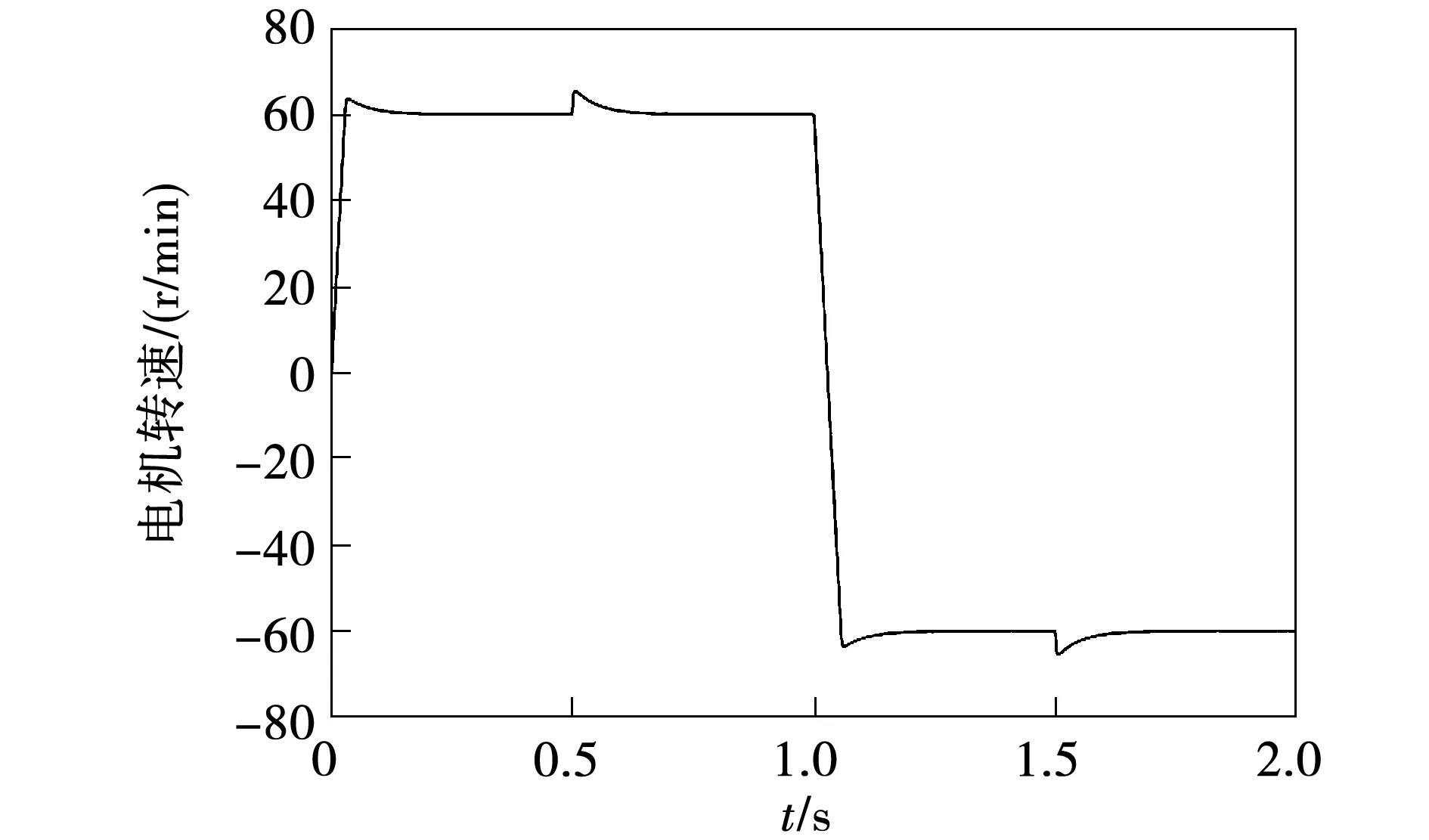
图7 基于MPTC控制的电机转速Fig.7 Motor speed using MPTC

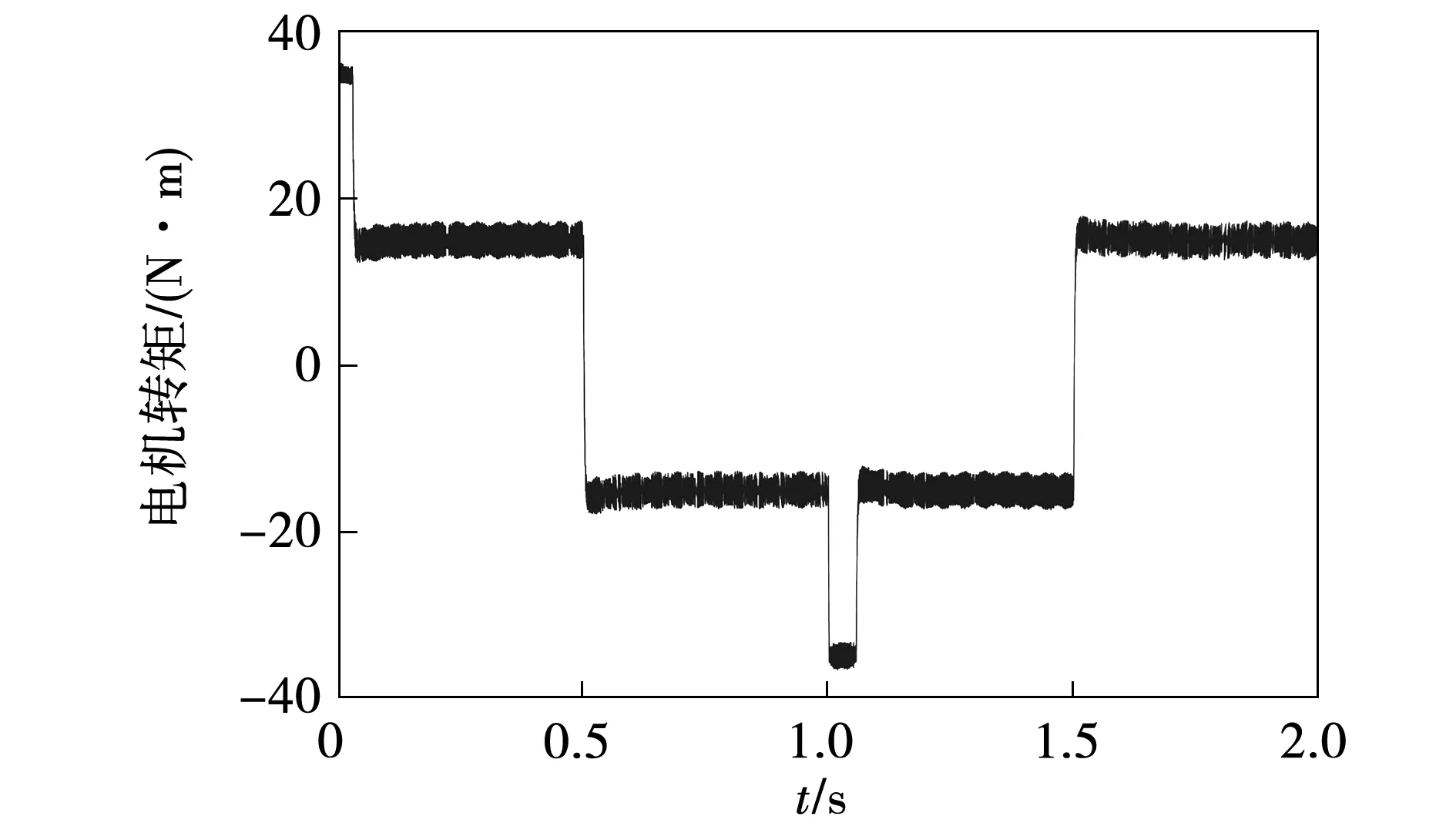
图8 基于MPTC控制的电机转矩Fig.8 Motor torque using MPTC

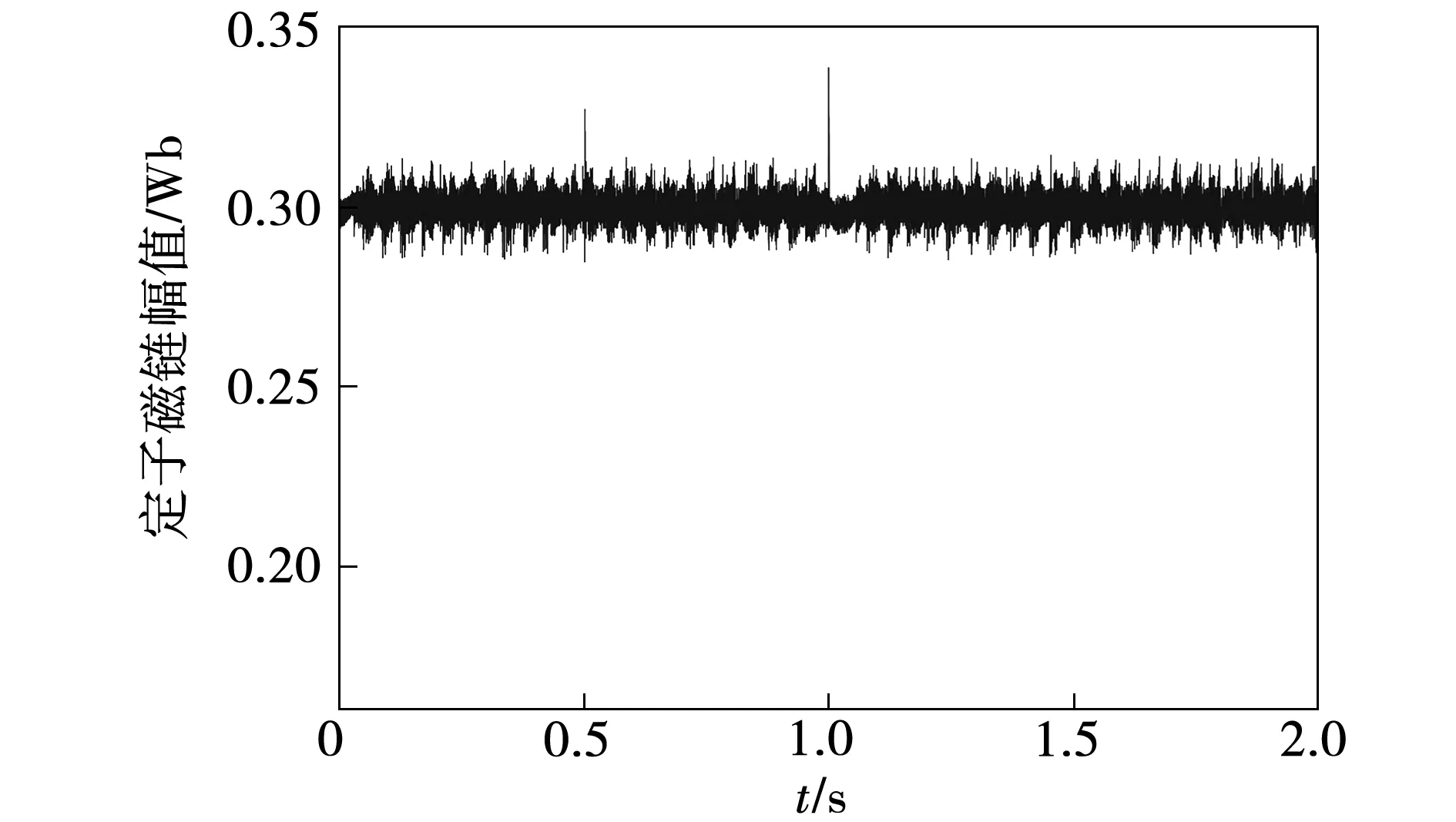
图9 基于MPTC控制的定子磁链幅值Fig.9 Amplitude of stator flux using MPTC

在0.2～0.4 s、0.6～0.8 s、1.2～1.4 s和1.6～1.8 s四个稳态时段内的转矩脉动RMSE和磁链脉动RMSE及平均值如表2所示。

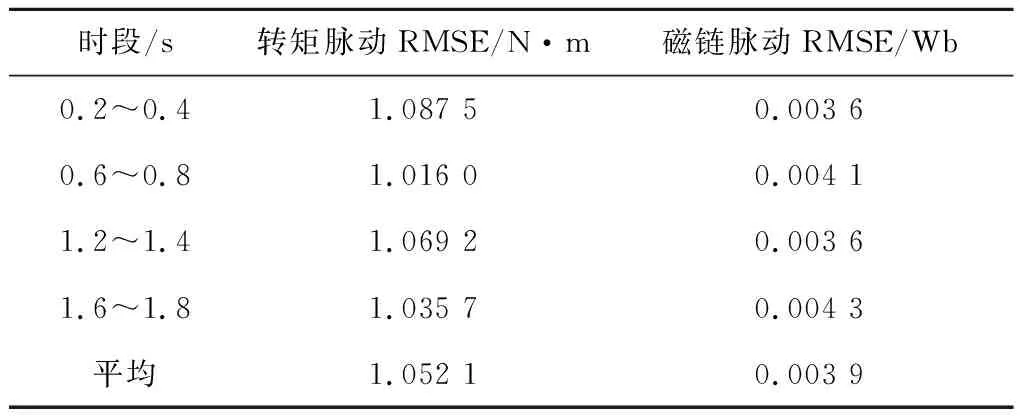
表2 MPTC控制下的转矩和磁链脉动RMSE

图7～图9和表2表明MPTC系统运行正常，但由于其需要遍历7个基本电压矢量进行枚举计算，计算负担较大。相同仿真条件下，采用DNN控制的仿真结果如图10～图12和表3所示。

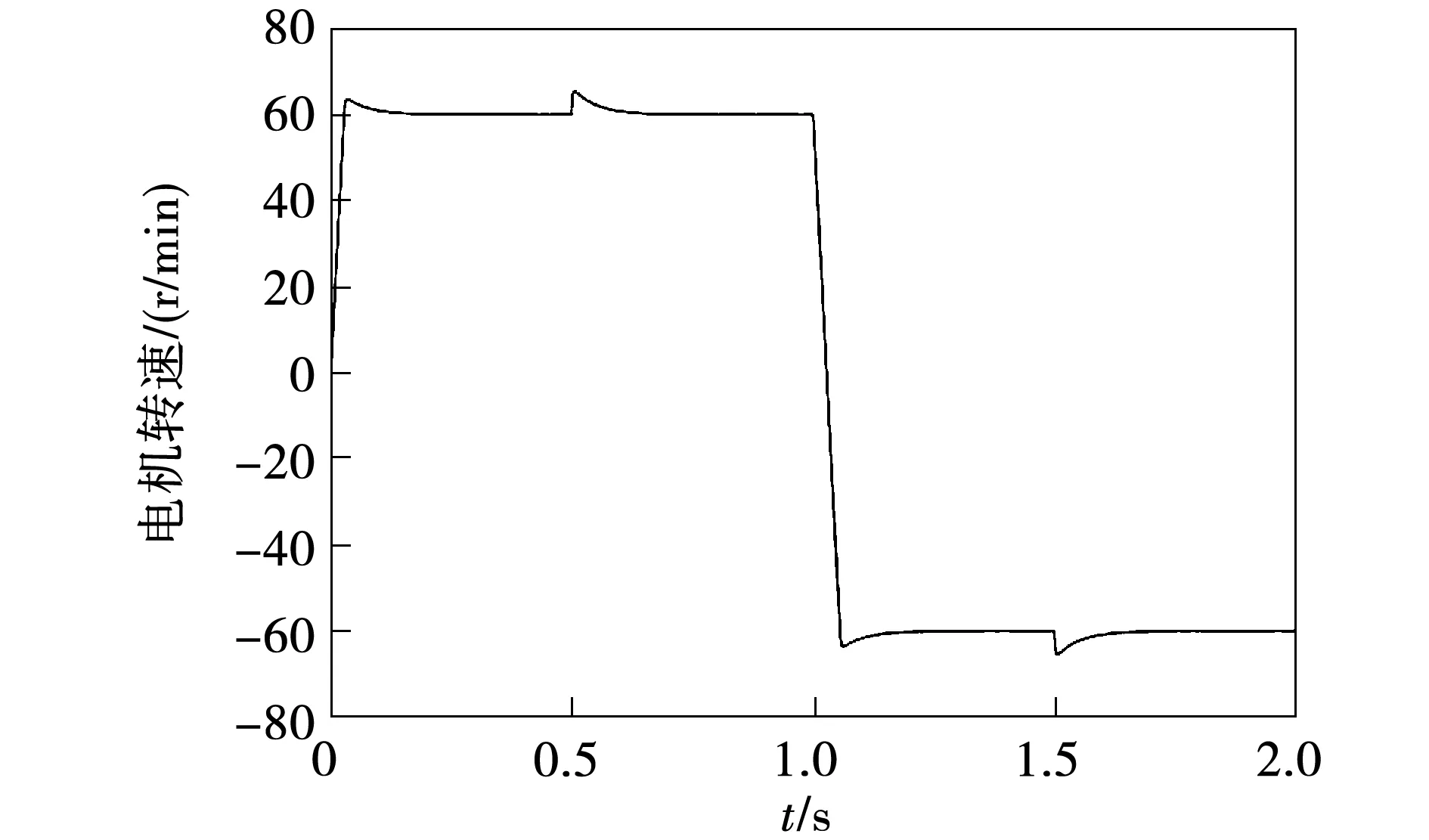
图10 基于DNN控制的电机转速Fig.10 Motor speed using DNN

图11 基于DNN控制的电机转矩Fig.11 Motor torque using DNN

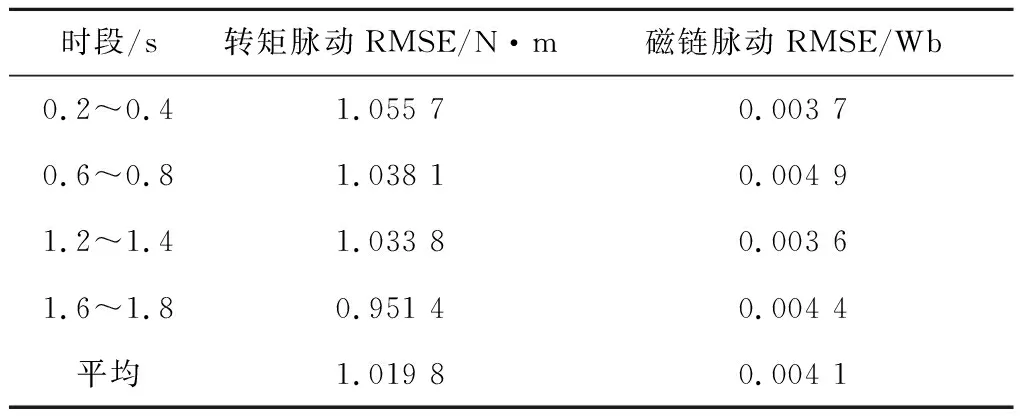
表3 DNN控制下的转矩和磁链脉动RMSE

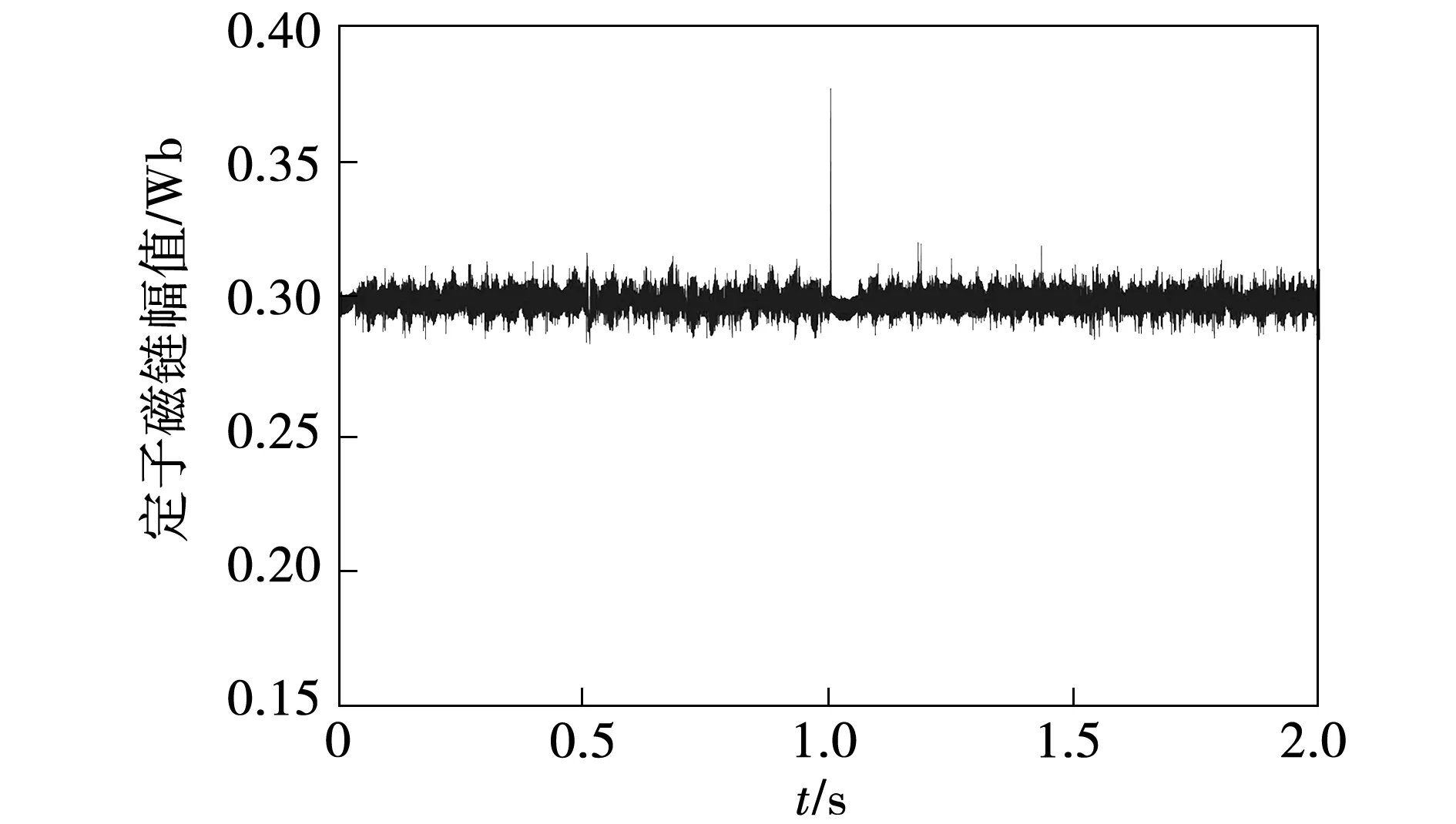
图12 基于DNN控制的定子磁链幅值Fig.9 Amplitude of stator flux using DNN

仿真结果表明：基于DNN的永磁同步电机系统运行正常，转矩和磁链控制效果良好，电机可实现四象限运行。稳态下，转矩和磁链的控制性能与MPTC基本相当，但在1s转速阶跃处产生较大的磁链脉动。

4 动态失控抑制

4.1 动静态数据失衡引起的系统失控

进一步研究发现在较大幅度的转速阶跃下，基于DNN的电机系统在转速阶跃处会出现失控现象。保持负载转矩不变，参考转速初始值设置为500 r/min，1 s时阶跃至-500 r/min。此时，基于DNN控制的电机系统失控，转矩和磁链波形如图13、图14所示。

图13 数据驱动控制失控时转矩波形Fig.13 Motor torque at the DNN out of control

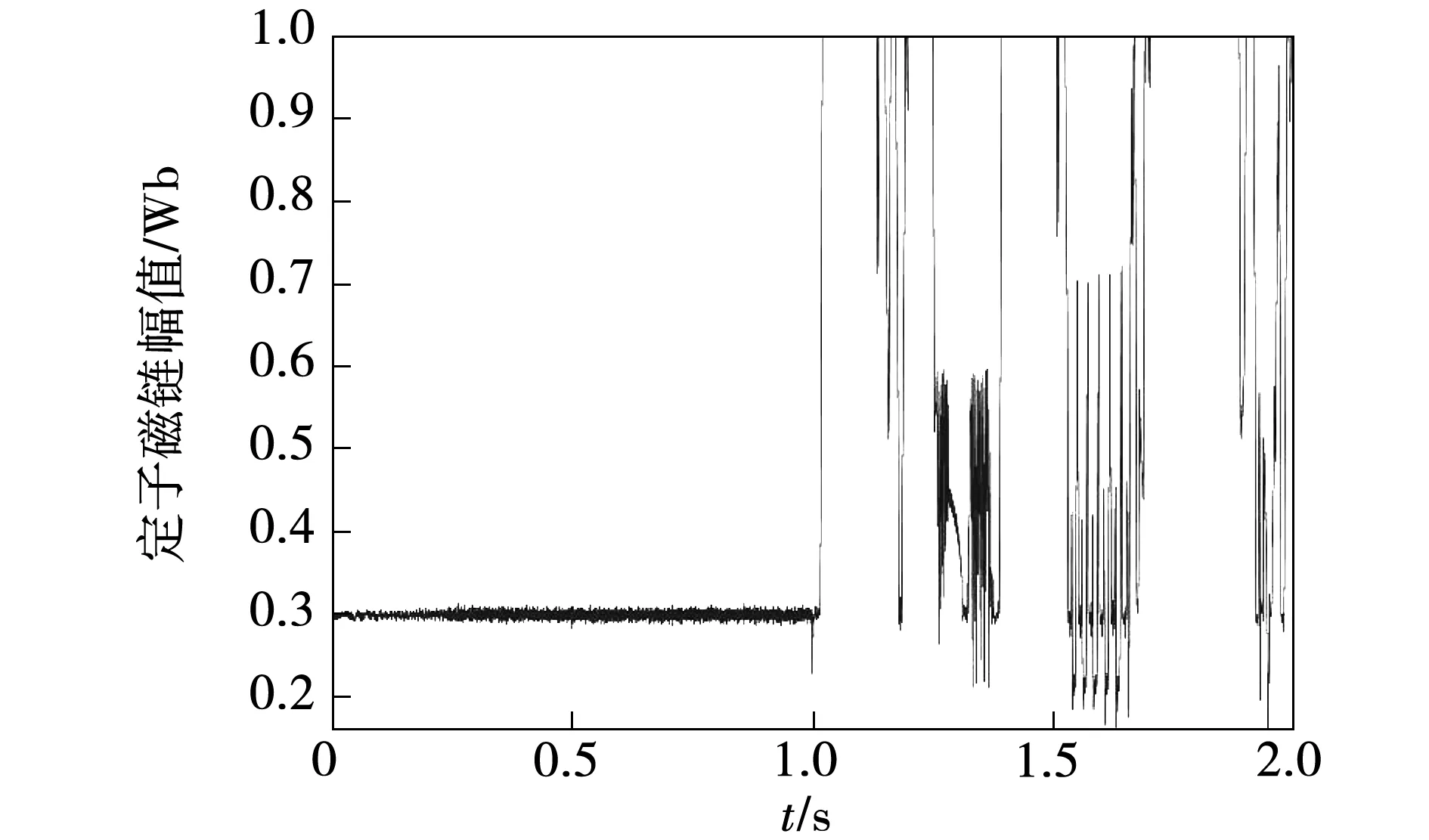
图14 数据驱动控制失控时磁链波形Fig.14 Amplitude of stator flux at the DNN out of control

在上述仿真条件下运行MPTC控制的永磁同步电机系统，同时并行运行DNN网络，DNN所选的电压矢量并不输出，仅用于与MPTC选择的电压矢量进行比较。统计0.25～0.45 s和0.55～1 s两段稳态时段和1～1.45 s发生转速阶跃的整个动态时段，MPTC所选电压矢量与DNN所选电压矢量的一致率如表4所示。

表4 MPTC与DNN输出电压矢量一致率

表4表明，稳态下DNN保持较高的准确率，但动态下准确率较低。

以0.01 s为单位统计0.55～1 s和1～1.45 s时间段内的电压矢量选择一致率，如图15所示。

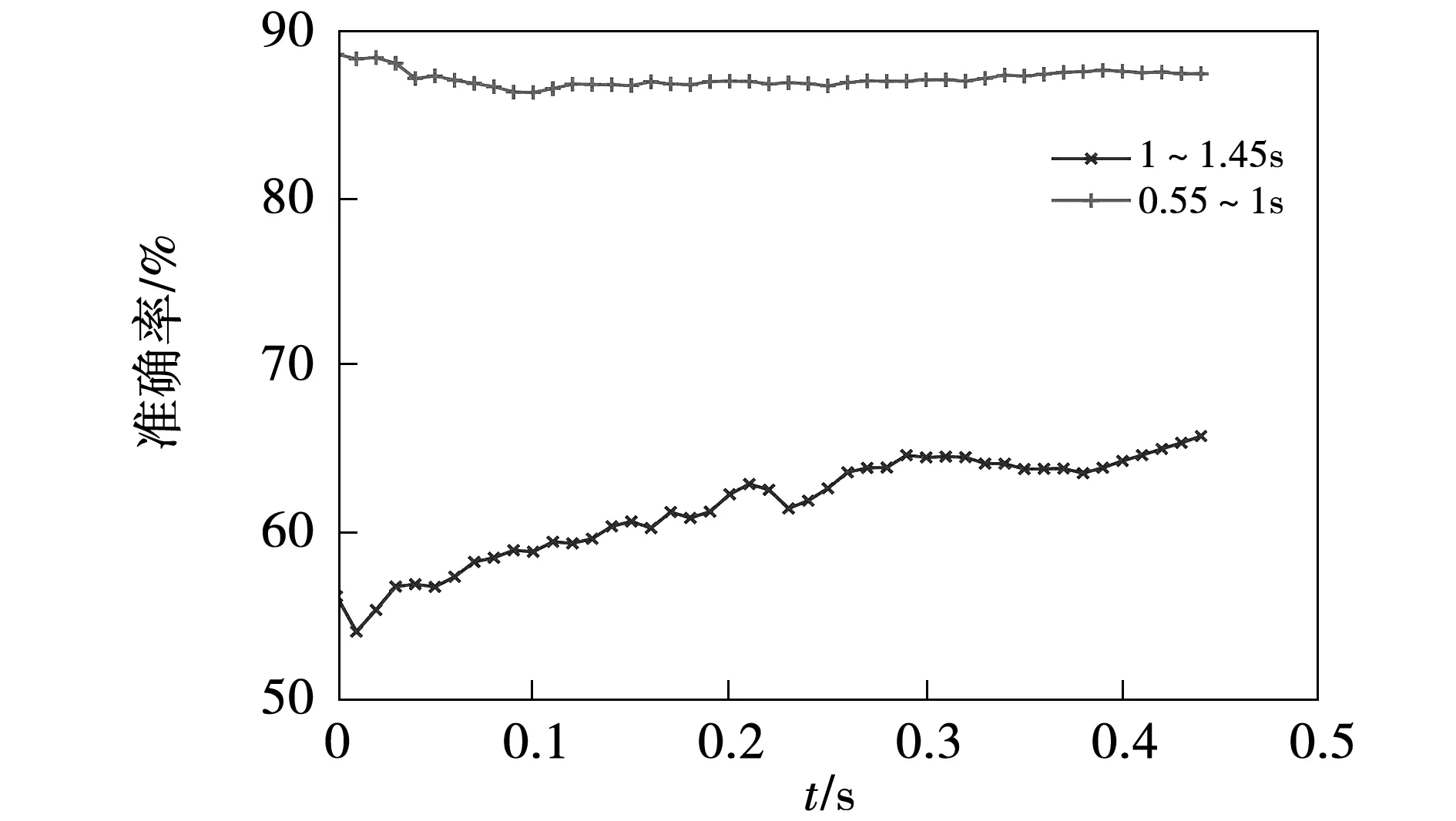
图15 输出电压矢量一致率变化曲线Fig.15 Concordance rate of output voltage vectors by MPTC and DNN

图15表明DNN在0.55～1 s稳态阶段始终保持着较高且稳定的准确率，但在1～1.45 s转速阶跃动态阶段，DNN所选电压矢量的准确率较低，尤其是发生转速阶跃的动态初始阶段，DNN错误选择电压矢量导致系统失控。

动态条件下，DNN选择电压矢量准确率较低的原因是MPTC在稳态和动态下选择电压矢量的倾向性存在较大的差异。采用式(7)所示的成本函数的MPTC在转矩动态变化下电压矢量选择规律与稳态选择规律有所不同，更倾向于选择转矩控制的电压矢量，牺牲磁链控制。由于动态响应较快，使得训练数据中反映动态阶跃控制规律的数据较少，稳态数据和动态数据失衡，导致神经网络动态训练不足，系统存在动态失控风险[24-25]。

4.2 综合数据集合

由于动态数据不足，使得基于动静态失衡数据驱动的DNN存在动态失控的风险。因此，通过扩充动态数据，使得动态数据与稳态数据达到基本平衡，建立综合数据集合，可抑制动态失控。

动态数据建立仿真条件如下：在[-500 r/min,500 r/min]转速范围内，设转速阶跃幅度为100、200、…、500 r/min，并在每种转速阶跃下分别设置负载转矩为-30、-20、-10、10、20、30 N·m，共计354组动态仿真条件。通过参考转矩判断系统动静态状态，共收集到1 208 610组动态训练样本。综合上文的稳态数据，从而建立2 208 610组综合数据集合，其中稳态数据和动态数据的比例约为1∶1。DNN的拓扑结构与训练设置与上文一致，仅将训练数据集更换为综合数据集合。通过网络训练，最终DNN在训练集和测试集的准确率可达82%。

在上述失控仿真条件下，基于综合数据集训练的DNN控制仿真结果如图16～图19所示。MPTC和基于综合数据集训练的DNN控制下，转矩脉动RMSE和磁链脉动RMSE及平均值如表5所示。仿真结果表明，基于综合数据集训练得到的DNN控制性能良好，电机系统可四象限运行，且可在保证稳态控制性能的基础上，有效解决动态失控问题。

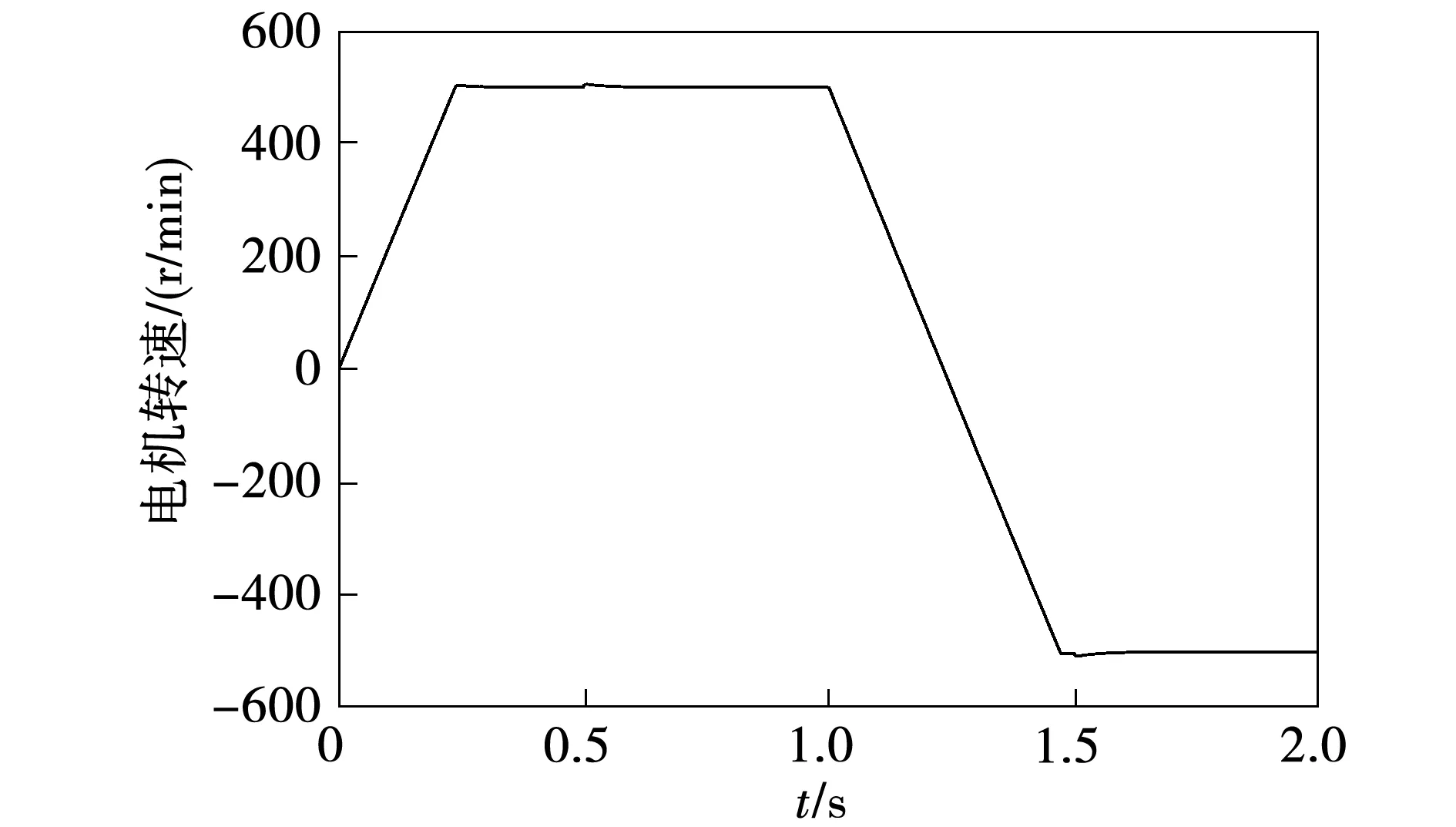
图16 电机转速Fig.16 Motor speed

图17 电机转矩Fig.17 Motor torque

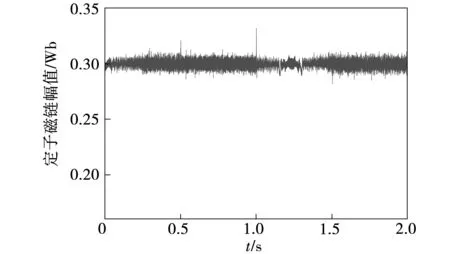
图18 定子磁链幅值Fig.18 Amplitude of stator flux

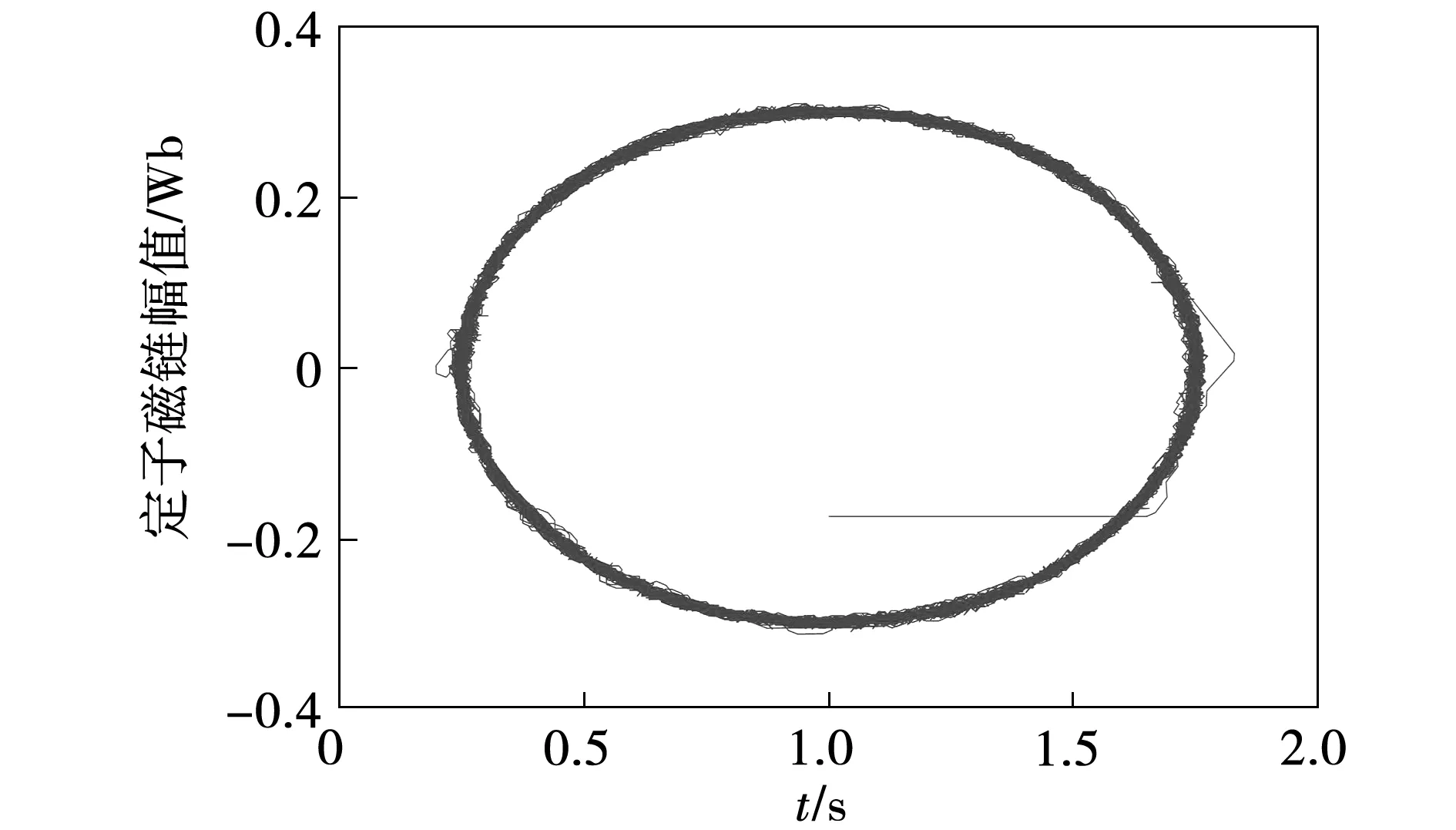
图19 定子磁链轨迹Fig.19 Stator flux circle

表5 MPTC和DNN控制下的转矩和磁链脉动RMSE

在0.55～1 s稳态时段和1～1.45 s动态时段内DNN与MPTC选择电压矢量的一致率如图20所示。

图20 一致率变化曲线Fig.20 Concordance rate of output voltage vectors by MPTC and DNN

图20表明基于综合数据集训练的DNN在转速阶跃时电压矢量选择准确率始终保持在84%以上，从而可有效抑制动态失控。

在上述仿真条件下运行DNN网络，同时并行运行MPTC控制，并根据成本函数对7个电压矢量进行升序排序。统计DNN输出电压矢量在MPTC成本函数的排序位置情况，结果如表6所示，其中1代表成本函数最小，即最优电压矢量，2代表成本函数次小，即次优电压矢量，以此类推。

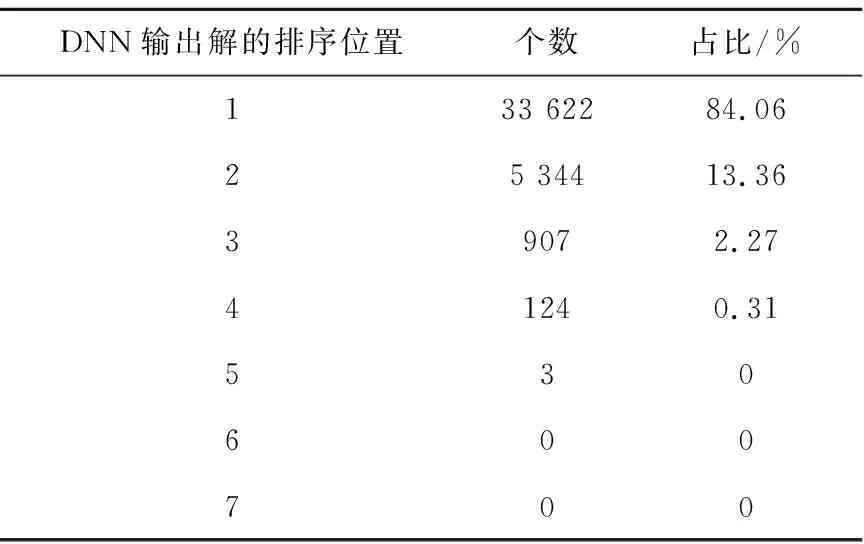
表6 DNN输出电压矢量在MPTC中排序位置

表6表明DNN输出的电压矢量约84%为最优电压矢量，输出为最优或次优电压矢量占比为97.42%。研究发现，MPTC始终选择次优电压矢量也可以使电机系统正常运行，即次优电压矢量也可作为可选电压矢量。DNN选择成本函数排序后4位电压矢量的概率接近为0。因此，这是DNN在准确率为82%的情况下依然可使电机系统正常运行的重要原因。

5 非线性约束下的数据驱动

仿真结果表明：MPTC控制下，在转矩动态变化及转速阶跃时，磁链会产生较大的脉动，如图21所示。这是因为式(7)所示的成本函数此时倾向于转矩控制，所选的电压矢量牺牲了磁链控制。由图18可知，转速阶跃时，基于MPTC数据驱动的DNN磁链脉动较大。

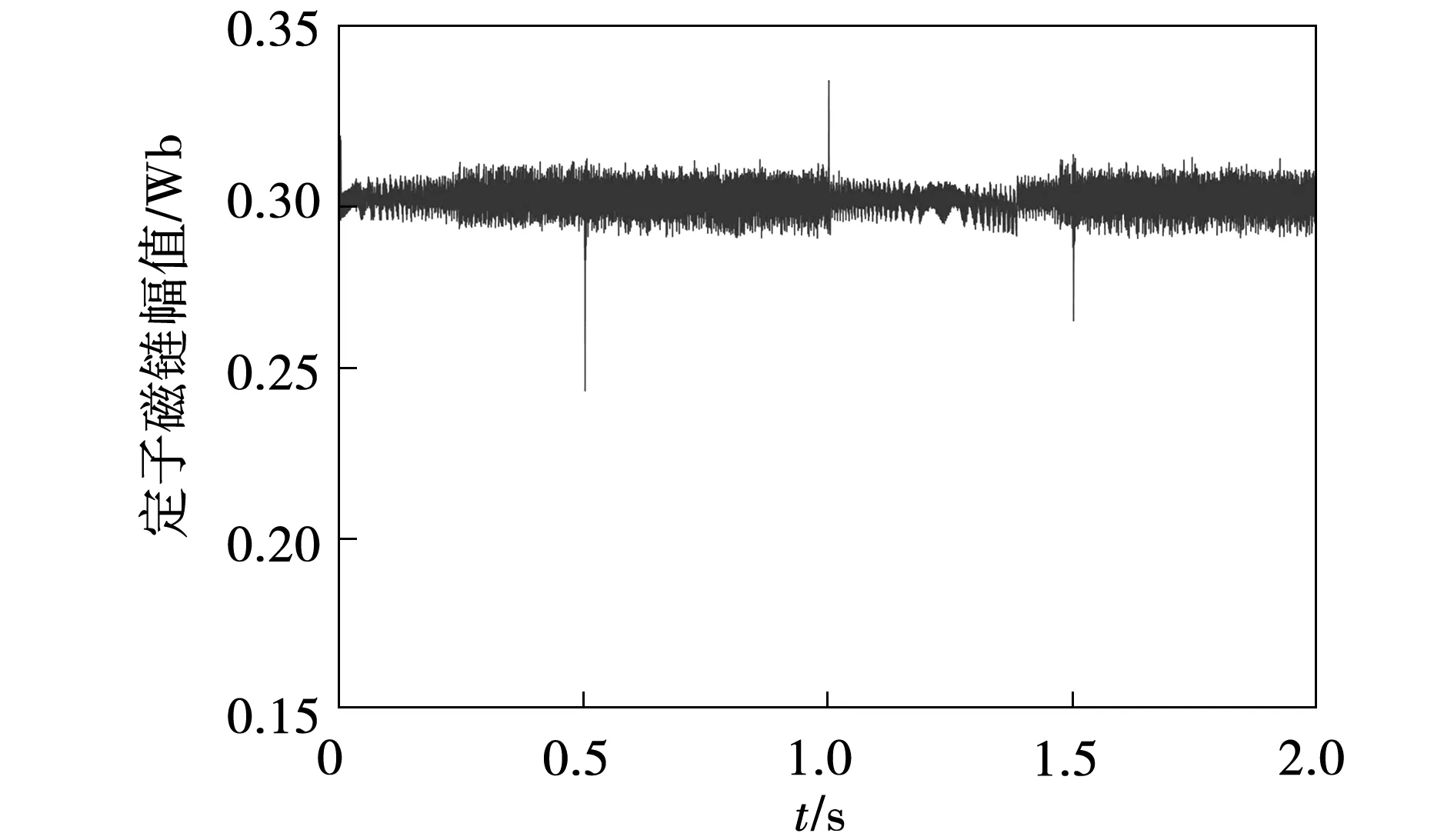
图21 基于MPTC控制的定子磁链幅值Fig.21 Amplitude of stator flux using MPTC

为了消除转速阶跃时的磁链脉动，设计考虑磁链约束成本函数为

g=

(13)

(14)

其中gf为防止选择使磁链误差较大电压矢量的非线性约束项。

相同仿真条件下，采用增加非线性约束成本函数MPTC控制的定子磁链幅值仿真结果如图22所示。稳态下，转矩和磁链脉动RMSE如表7所示。仿真结果表明：增加非线性约束可有效抑制转矩动态变化时的磁链脉动。

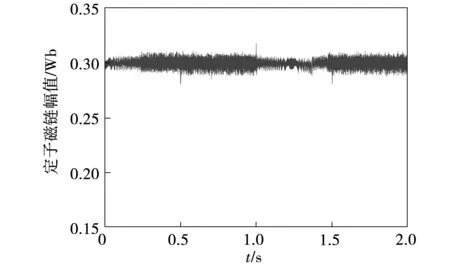
图22 非线性约束成本函数MPTC控制下的定子磁链幅值Fig.22 Amplitude of stator flux using MPTC

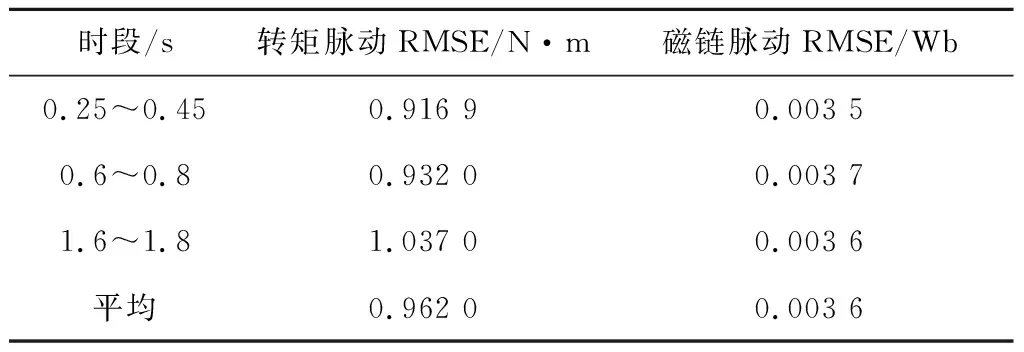
表7 增加非线性约束成本函数MPTC控制下的转矩和磁链脉动RMSE

与上文训练数据集合建立方法相同，基于增加非线性约束成本函数的MPTC重新建立训练数据集。在训练样本数量、DNN网络结构与参数、训练方法相同的条件下，仅更换训练数据集，对DNN网络重新训练。最终DNN在训练集和测试集的准确率可达82%。

相同仿真条件下，DNN控制下的定子磁链幅值仿真结果如图23所示。稳态下，转矩和磁链脉动RMSE如表8所示。

图23 基于非线性约束数据的DNN控制下定子磁链幅值Fig.23 Amplitude of stator flux using DNN

表8 基于非线性约束数据的DNN控制下的稳态控制效果

当1 s发生转速阶跃时，四种控制策略下的最大定子磁链幅值如表9所示，其中MPTC、DNN、MPTC(gf)和DNN(gf)分别代表模型预测转矩控制、基于MPTC数据驱动的DNN控制、非线性约束成本函数MPTC控制和基于非线性约束数据驱动的DNN控制。

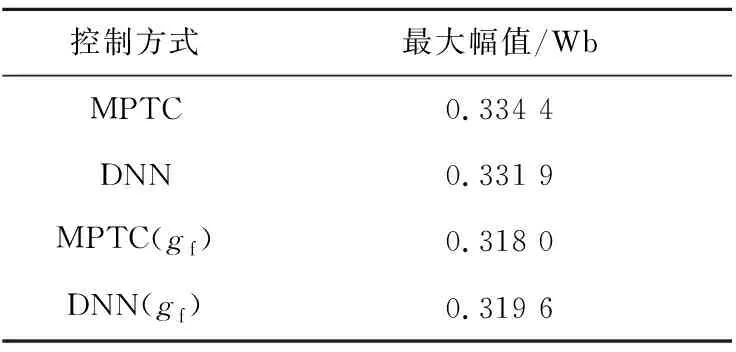
表9 四种控制方式下的定子磁链脉动比较

仿真结果表明：基于非线性约束数据驱动的DNN控制下，稳态控制效果与非线性约束成本函数MPTC控制MPTC基本相当，且可有效抑制转矩动态变化时的磁链脉动，说明通过基于数据驱动的DNN可学习并取代非线性约束下的控制规律。

6 结 论

本文提出了基于数据驱动永磁同步电机神经网络控制以取代模型预测转矩控制的方法，将计算量大、实时性差的遍历寻优计算转换为线下网络训练，线上运算仅进行快速推理和分类选择，以满足实时性要求，得出结论如下：

1)基于数据驱动的神经网络控制可取代模型预测转矩控制。基于DNN的永磁同步电机系统运行良好，可实现四象限运行，稳态转矩和磁链的控制性能与MPTC基本相当，对采用多电平逆变器或矩阵变换器驱动或采用多步预测等备选电压矢量数目较多的场合有较大的应用意义。

2)通过扩充动态数据集合，可解决因动静态数据失衡引起的系统失控问题。

3)基于数据驱动的DNN可以学习非线性约束下的控制规律，表明数据驱动控制方式具有较强的可行性，可适用于模型预测控制多目标、非线性控制的复杂规律场合。